Avete voluto la matematica? E ora ve la “beccate”! Sto scherzando, dato che sarà una matematica alla portata di tutti coloro che vogliono applicarsi soltanto qualche minuto in più del solito.

Il lobo di Roche è ormai un vecchio amico che abbiamo incontrato varie volte quando si è parlato di stelle doppie quasi a contatto e che ci ha permesso di definire il celeberrimo punto lagrangiano L1, l’unica porta sempre aperta per lo scambio di materia tra due stelle vicine. Lo abbiamo già confrontato con il limite di Roche che, invece, riguarda un punto critico della distanza di un corpo soggetto alla forza di marea di un altro più grande. Non eravamo, però, entrati nei dettagli.

Ormai abbiamo verificato che a molti lettori piace la matematica e quindi mi sono deciso a usarla per determinare questo limite, così importante per trasformare un satellite compatto in una nuvola di detriti e, infine, in una bellissimo anello. Questa volta, la matematica sarà veramente elementare, tale da essere seguita da tutti coloro che hanno raggiunto un livello di scuola media inferiore. Sarebbe stato più rapido (e semplice) utilizzare una “bella” derivata, ma per quella dobbiamo aspettare che il nostro piccolo “corso” di matematica vada ancora un po’ avanti. Vi prego di seguire con attenzione la trattazione e vi accorgerete che ogni passaggio è veramente “infantile”. Non spaventatevi! E poi, al limite, chiedete senza paura. Ormai, tra noi, la vergogna è una parola dimenticata.

Abbiamo già descritto la forza di marea e abbiamo anche visto i suoi effetti sul riscaldamento del satellite di Giove, Io. Essa deforma un satellite (o un pianeta) obbligandolo ad allungarsi nella direzione del pianeta. E’ anche lei che causa le maree oceaniche sulla Terra e obbliga un satellite a mostrare sempre la stessa faccia al suo pianeta. Per ottenere questo bisogna lavorare sul momento angolare (una grandezza fisica che domina veramente l’Universo e le sue rotazioni) e far sì che si conservi sempre (la solita pattinatrice sul ghiaccio). Ne segue che il satellite può tendere ad allontanarsi o ad avvicinarsi al pianeta a seconda della sua velocità di rivoluzione rispetto a quella di rotazione del pianeta. Per richiamare questi concetti vi prego di andare QUI, o -ancor meglio- su Rosetta o il Teatro dove la marea è spiegata in grande dettaglio “divulgativo”.

Questa volta, invece, otterremo matematicamente la forza di marea durante il calcolo che ci porterà al limite di Roche.

Consideriamo la Fig. 1 che ci mostra la situazione in cui lavoriamo. A sinistra vi è un grande pianeta (come, ad esempio, Saturno) e a sinistra vi è un piccolo satellite (ma non “troppo” piccolo) come vedremo più in là. Il pianeta ha raggio R e massa M, mentre il satellite ha raggio r e massa m. La loro distanza è D. Per potere giungere fino in fondo dobbiamo assumere che r sia molto più piccolo della distanza D. Ma questa è una situazione più che normale.

La domanda che ci facciamo è la seguente: “A che distanza D dal pianeta può avvicinarsi  il satellite prima che la forza di marea lo frantumi completamente trasformandolo in una nuvola di frammenti?” Questo limite di sopravvivenza prende il nome di limite di Roche.

Per essere più semplici nella trattazione, consideriamo il nostro satellite formato da due sfere uguali  di raggio r e di massa m. Le cose non cambiano di certo rispetto alla Fig.1, ma ci permettono un calcolo molto più intuitivo. Dobbiamo assumere un’altra ipotesi di partenza (che alla fine discuteremo): le due sfere stanno attaccate SOLO a causa della forza gravitazionale reciproca. Non vi sono quindi forze di coesione della materia che complicherebbero la trattazione in modo terribile. In realtà, questa ipotesi non è poi così strana, se pensiamo che gli asteroidi e probabilmente molti satelliti medio-piccoli non sono altro che ammassi di blocchi di pietra o di ghiaccio tenuti insieme dall’autogravitazione.

Ne abbiamo già parlato riguardo alla vita collisionale degli asteroidi (QUI) e accennato quando abbiamo parlato della vita avventurosa dei satelliti di Saturno, che, probabilmente, si sono frantumati più di una volta nella loro vita a causa di impatti catastrofici con comete di passaggio. Essendo più lontani del limite di Roche sono riusciti a ricostruirsi (vedi Mimas, ad esempio), come ha fatto la Luna attraverso i frammenti della nostra Terra.

Torniamo al nostro satellite “diviso” in due parti a stretto contatto e disegniamo la Fig. 2.

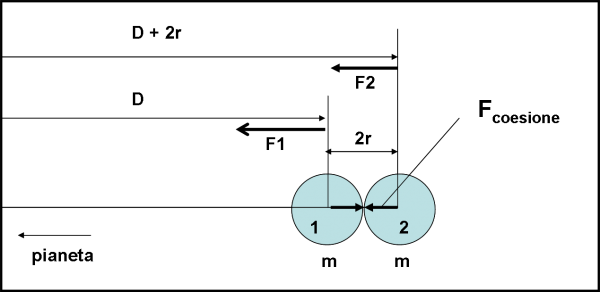
Calcoliamo, innanzitutto, la forza di gravità che tiene unite le sue sferette di raggio r e di massa m (il nostro “speciale” satellite).  Basta richiamare la legge di Newton che ci dice che la forza gravitazionale è data dal prodotto delle masse in gioco, diviso per il quadrato della distanza tra i rispettivi baricentri (in caso di sfere il baricentro è il loro centro). Il tutto è moltiplicato per una costante G, il cui significato possiamo tranquillamente tralasciare. Scritta “matematicamente” e in modo generale, diventa:

F = G m1 m2/d²               ….  (1)

Nel nostro caso, con due sfere di massa m e di raggio r (a contatto), si scrive:

F_coesione = Gmm/(2r)² = Gm²/4r²             ….  (2)

L’abbiamo chiamata forza di coesione (un nome non proprio azzeccato) dato che è quella che tiene attaccate le due sfere (ma si basa solo sulla reciproca gravità). La distanza tra i due centri è ovviamente 2r, mentre m è la stessa per entrambe.

Vediamo, adesso, quale forza gravitazionale subiscono le due sfere per effetto del pianeta di massa M, posto a distanza D.

La sfera più vicina a lui subisce una forza di gravitazione pari a:

F1 = GMm/D²                     ….  (3)

Mentre la sfera più lontana subisce una forza

F2 = GMm/(D+2r)²            ….  (4)

Cosa ci dicono queste due forze? Una cosa molto semplice: il pianeta attira verso di sé in modo maggiore la sfera 1 che non la 2, dato che quest’ultima si trova leggermente più distante. Questo fatto lo vediamo confrontando la (3) con la (4). La seconda è una forza più piccola dato che è uguale a quella precedente a parte il denominatore. Anche se di poco, esso è più grande e quindi la forza che ne deriva è più piccola. Questa differenza di forze tra la sfera più vicina e quella più lontana, tende a separare le due sfere (una è attirata di più dell’altra). In altre parole, possiamo dire tranquillamente che la differenza tra le forze si comporta come una forza unica che tende a “stirare” l’oggetto formato dalle due sfere e, se possibile, separarle, ossia distruggere il satellite. Questa forza non è altro che la Forza di Marea, dovuta proprio alla differenza di gravità che subiscono i due estremi di un unico corpo solido (nel nostro caso tenuto insieme solo dall’autogravitazione).

Per scriverla matematicamente, ci basta fare la differenza tra F1 e F2. Quello che troveremo sarà proprio la forza di marea, indotta dal pianeta di massa M a distanza D su un satellite formato da due masse m a contatto. Capite bene che il discorso semplificato non sarebbe cambiato assolutamente se avessi preso, come satellite, una sfera unica. Avrei, comunque, avuto un emisfero più vicino e uno più lontano. Il discorso non si sarebbe modificato, ma la trattazione sarebbe stato molto più complicata.

F1 – F2 = GMm [1/D² – 1/(D+2r)²] = GMm A        ….  (5)

Per meglio seguire i passaggi successivi (ridondanti) ho chiamato A  la parte dentro alla parentesi quadra, dopo aver messo in evidenza la parte comune alle due espressioni delle forze.

A = 1/D² – 1/(D+2r)² = [(D + 2r)² – D²]/ [D² (D+2r)²]

A = (D² + 4r² + 4Dr – D²)/ [D² (D+2r)²] = (4r² + 4Dr)/ [D² (D+2r)²] = 4r (r + D)/ [D² (D+2r)²]

Ossia abbiamo

A = 4r (r + D)/ [D² (D+2r)²]            ….  (6)

Fin qui ho solo usato passaggi di aritmetica elementare (massimo comun divisore, quadrato di un binomio e cosucce del genere) … è vero oppure no?

A questo punto dobbiamo fare una piccola approssimazione, tenendo conto dell’ipotesi fatta fin dall’inizio, quando abbiamo detto che il raggio r delle sfere deve essere molto più piccolo della distanza D dal pianeta. Possiamo quindi scrivere in modo “simbolico”:

r << D, ma anche 2r << D. Se r è molto piccolo, lo è anche 2r. In queste condizioni, si può anche dire che r è trascurabile rispetto a D e quindi:

r + D ~ D

…. (7)

D + 2r ~ D

Attenzione si può scrivere D + r = D, ma non D r = D

Verifichiamolo con numeri “veri”. Poniamo che D sia uguale a 100 000 e che r sia solo 3. Bene, aggiungendo a 100 000 il numero 3 o il numero 2 ∙ 3 = 6, il risultato cambia di poco. 100 003 o 100 006 possono essere considerati ancora 100 000. Ben diversa sarebbe la situazione se avessimo 100 000 ∙ 3 o 100 000 ∙ 6.  In questo caso, 300 000 e 600 000 sono ben diversi da 100 000.

Sostituiamo allora le approssimazioni  (7) nella  (6), ottenendo:

A ~ 4rD/D⁴ = 4r/D³

Sostituendo A nella (5), si ha

F1 – F2 = 4GMmr/D³     ….  (8)

Questa è la formula (lievemente approssimata) che  descrive matematicamente la forza di marea. Notate un fatto importante (che spesso si sente dire): la forza di marea decresce con il cubo della distanza (e non con il quadrato come fa la forza gravitazionale). Inoltre, oltre a dipendere direttamente dalle masse in gioco, dipende anche dal raggio del satellite che la subisce. In più compare anche un fattore 4 (ma quello è molto meno importante). La dipendenza dal raggio r è abbastanza ovvia, dato che a parità degli altri parametri, più il corpo è allungato e più la differenza tra la parte vicina e quella lontana aumenta. Riscriviamo la (8) chiamandola proprio forza di marea:

F_marea = 4GMmr/D³      ….  (9)

Beh, ragazze e  ragazzi, abbiamo già ottenuto un risultato niente male. Siamo riusciti a ricavare la formula che descrive la forza di marea senza bisogno di fare una derivata che sarebbe stata la più ovvia decisione. Lo vedremo meglio quando gli articoli sulla matematica elementare arriveranno a questo punto.

Torniamo al nostro satellite che è soggetto a due forze contrastanti: una è quella gravitazionale tra le due sfere che tende a farlo stare unito. L’altra è quella di marea che tende a separare le due sfere e a distruggerlo.

Per sapere a che distanza riesce a vincere quella di marea, basta scrivere la diseguaglianza:

F_marea > F_coesione

Ossia:

4GMmr/D³ > Gm²/4r²          …. (10)

Ricordiamo che le semplificazioni nelle diseguaglianze seguono le stesse regole delle uguaglianze e si possono portare termini da un lato all’altro senza problemi. Possiamo, allora scrivere:

4 Mr/D³ > m/4r²

16 M/D³ > m/r³

16 M > D³ m/r³

16 Mr³/m > D³

E infine isolare D, che compare al cubo

D³ < 16M r³/m         …. (11)

A questo punto, notiamo che conosciamo sia il raggio del pianeta R che il raggio del satellite r, per cui possiamo scrivere la massa come volume moltiplicato per la densità ρ dell’oggetto celeste. Ricordiamo, infatti, che si definisce densità il rapporto tra la massa e il volume del corpo. Essa ci dice che tipo di materia vi è all’interno. Se fosse composto d’acqua avremmo una densità uguale a 1. Se fosse composto di ferro, la massa, a parità di volume, sarebbe ben maggior e quindi la densità sarebbe molto più grande. Se invece fosse di panna montata la densità scenderebbe sotto all’unità. E via dicendo.

Ricordando che il volume V di una sfera di raggio r è dato da 4/3πr³, le masse diventano:

M = V_P ρ_P = 4πR³ ρ_P /3

e

m = V_S ρ_S = 4πr³ ρ_S /3

Sostituendole nella (11), la diseguaglianza diventa (non spaventatevi e provate a farlo da soli!), con qualche semplificazione:

D³ < 16 (4πR³ ρ_P /3) r³/ (4πr³ ρ_S /3) = 16 R³ ρ_P/ ρ_S

ossia:

D³ < 16 R³ ρ_P/ρ_S         …. (12)

Uffa! Abbiamo ancora il cubo che ci dà un po’ fastidio. Nessun problema. Basta eseguire la radice cubica di entrambi i membri della diseguaglianza. Per i meno preparati, ricordiamo che la radice cubica di un numero N  è il numero m che bisogna elevare al cubo (ossia moltiplicare per se stesso tre volte) per ottenere il numero N. Invece di usare il solito simbolo di radice, non ben definito nella scrittura al PC, usiamo la notazione di frazione. La radice quadrata si indica con l’elevazione a 1/2, quella cubica a 1/3 e via dicendo.  Si ottiene:

D < (16)^1/3 R (ρ_P/ρ_S)^1/3

e, infine:

D < 2.5 R (ρ_P/ρ_S)^1/3       …. (13)

Il numero esatto sarebbe un po’ più piccolo (2.46 circa), ma possiamo tranquillamente usare 2.5 viste le incertezze in gioco e la maggiore facilità mnemonica di 2.5.

Ovviamente, se il pianeta e il satellite hanno la stessa densità, la formula si semplifica ancora di più e diventa:

D < 2.5 R       …. (14)

Il valore di D definisce il limite di Roche relativo a un pianeta di raggio R. Visto? Ce l’abbiamo fatta alla grande!

E’ necessario fare qualche piccola considerazione. Abbiamo considerato il satellite tenuto insieme solo dall’autogravitazione. In realtà, la materia si lega anche attraverso altre forze, quelle di stato solido, ad esempio. Pensiamo, infatti, che gli atomi e le molecole si abbracciano con grande passione e per separarle ci vuole un po’ più di fatica. Tuttavia, in molti casi possiamo tranquillamente pensare a corpi celesti formati da blocchi separati che stanno uniti tra loro proprio grazie all’autogravitazione. In fondo, fanno così anche le stelle… Quindi, il limite di Roche è normalmente utilizzabile, ad esempio nel sistema di Saturno, dove i satelliti medio-piccoli hanno  sicuramente subito qualche distruzione catastrofica e la susseguente ricostruzione. Per loro il modello basato sull’autogravitazione è più che realistico.

Potremmo anche pensare di utilizzare la formula pensando al sistema Terra-Luna. Fortunatamente, il gioco di rotazione e rivoluzione e di marea sta allontanando la Luna. Ma in altri casi potrebbe capitare proprio il contrario. A che distanza si distruggerebbe la Luna per effetto della forza di marea? Sarebbe facilissimo calcolarlo dalla (14), assumendo che le densità possano essere considerate uguali (in realtà non è affatto vero). Avremmo:

D < 2.5 ∙ 6000 = 15 000 km

Sarebbe uno spettacolo affascinante e terribile. Purtroppo, la Luna non è tenuta assieme solo dall’autogravitazione e, inoltre, ricordiamoci che la formula è valida solo se il raggio del satellite è molto più piccolo della distanza tra lui e il pianeta. E questo non è certo il caso della Luna. Il suo raggio di 1700 km è comparabile con 15 000 km. Niente da fare, la Luna ci piomberebbe addosso senza sgretolarsi, se non in maniera molto superficiale.

Ben diverso è stato il risultato della cometa Shoemaker-Levy 9 che nel 1993 si è frantumata completamente per effetto della marea di Giove.

Concludiamo con Saturno, il Signore degli anelli.

Prendiamo un bel satellite ghiacciato (un po’ come Mimas) e avviciniamolo al pianeta. Quando si distruggerà dando luogo a una miriade di frammenti, che poi si trasformeranno nell’anello (o anelli, dato che sono separati da risonanze che vietano la presenza di frammenti a certe distanze particolari)? Ce lo dice il limite di Roche. Basta calcolarlo, tenendo presente che il raggio di Saturno è di circa 60 000 km. La densità del pianeta è circa 0.7, mentre per il satellite possiamo considerarla uguale a 1 (quella dell’acqua, dato che molte lune di Saturno sono, in realtà, enormi palle di ghiaccio). Sostituendo nella (13), si ottiene:

D < 2.5 ∙ 60 000 ∙ (0.7/1)^1/3 = 133 000 km

Le osservazioni ci dicono che gli anelli (principali) arrivano fino a circa 140.000 km. Con le approssimazioni fatte, direi che possiamo considerarci più che soddisfatti. Il limite di Roche funziona davvero!

Qualcuno potrebbe dirmi (e tra di voi ce ne sono di certo ... furbacchioni!): “Eppure quello che dici non è vero! Innanzitutto perché i blocchi di ghiaccio degli anelli non si distruggono fino a diventare polvere. Inoltre, so benissimo che ci sono almeno un paio di satelliti che si nascondono tra gli anelli”.  Avrebbe sicuramente ragione, ma non terrebbe conto che in un corpo molto piccolo chi tiene insieme la materia non è più la gravità, ma le già citate forze di coesione della materia, ben più resistenti della gravità. Se lanciamo un  sasso da un altezza di 15000 km verso la Terra non si disintegrerebbe certo per la forza di marea, ma solo per l’attrito con l’atmosfera. Insomma, il limite di Roche è applicabile solo per oggetti abbastanza grandi, tali che l’autogravitazione abbia il ruolo più importante nel tenerli insieme.

Abbiamo parlato di satelliti, ma il discorso vale anche per un pianeta e una stella: guai ad avvicinarsi troppo. Perfino un buco nero galattico distrugge le stelle utilizzando la sua forza di marea. Ed è l’intera galassia, con la sua massa, che deforma e frantuma una galassia più piccola. Essa è proprio tenuta insieme solo dalla gravità mutua e i “blocchi” che si separano l’uno dagli altri sono proprio le stelle o dei loro gruppi. Insomma, la marea “distruttiva” è un fenomeno ben più generale rispetto alla “nostra” marea oceanica, che è solo un caso molto particolare e di lieve entità (fortunatamente!).

La prossima volta che guarderete Saturno, con un binocolo o con un telescopio di alta tecnologia, penserete a quel disco attorno al pianeta come a un qualcosa di ben più affascinante. Rifletterete sulla sua vita avventurosa, sulla sua creazione; vi sembrerà di poter vedere il limite di Roche; capirete la fortuna dei satelliti che guardano il tutto al di là del limite di sicurezza.  Scorgerete gli enormi blocchi di ghiaccio che ricordano i tempi antichi, comprenderete perché ci sono delle strisce vuote e immaginerete gli scontri continui tra quegli “iceberg” cosmici. Vi accorgerete che state vedendo Saturno così da vicino che sembra quasi di poterlo toccare e che non c’è oculare che tenga.

Avrete un vostro oculare potentissimo, quello della mente, della conoscenza e della fantasia.

Salutatemelo!