Categorie: Curiosità Fisica classica
Tags: momento angolare
Scritto da: Vincenzo Zappalà
Commenti:59
Tocca a voi! **
Non cominciate a sbuffare… Ho deciso di inserire, di tanto in tanto, un piccolo esercizio per “tastare” il polso delle conoscenze acquisite. Questa volta prendo spunto dal nostro amico Supermagoalex che è alle prese con la conservazione del momento angolare. Un fenomeno che tutti conosciamo in quanto è proprio quello che fa girare sempre più veloce una pattinatrice sul ghiaccio, se avvicina le braccia al corpo. E’ lo stesso fenomeno che fa girare le stelle di neutroni come trottole impazzite. Inoltre, a proposito di trottole, l’esercizio ha uno stretto legame con un fenomeno ancora più conosciuto (anche se più complicato): la precessione.
La soluzione non è assolutamente difficile (teoricamente), ma necessità una buona comprensione del significato di momento angolare e della sua conservazione. Non abbiate, quindi, nessuna paura di sbagliare e di esprimere i vostri ragionamenti. Lo scopo è quello di imparare e l’ignoranza è un requisito fondamentale. Quando si parla tra persone che non hanno timore di far lavorare la propria mente, tutto è ammesso!
Ecco, allora, l’esercizio che vi propongo. Potevo renderlo ancora più pratico pensando direttamente una persona seduta su una sedia girevole. Il disegno, però, diventava complicato e allora ho schematizzato la situazione, come mostrato in Fig. 1.
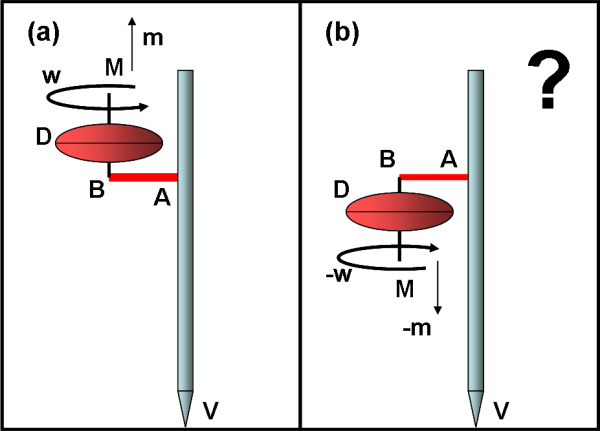
Consideriamo in Fig. 1(a) una bella matitona azzurra in posizione verticale, con la punta V che tocca il pavimento, ovviamente perfettamente liscio. Su di essa inseriamo una piccola barra AB, che può essere fatta ruotare attorno ad A, ma che una volta ruotata può nuovamente essere bloccata. Sulla sua estremità B inseriamo un’altra barra MB che può girare attorno a B. Ovviamente, in B vi è una specie di cerniera che permette la rotazione ma che tiene ancorate MB e BA. Inseriamo un disco D dentro alla barra MB e mettiamolo in rapida rotazione attorno a MB.
Il disco può ruotare, ma non può scorrere su e giù lungo l’asse di rotazione MB. Immaginate che il disco sia, ad esempio, una ruota di bicicletta che gira intorno al suo asse MB. Tutto deve essere perfetto (non vi sono attriti o angoli strani). La situazione è perfettamente stabile. L’unica cosa che si muove è la trottola che gira attorno al suo asse. Essa può continuare a ruotare per un tempo lunghissimo senza mai rallentare.
Come vi dicevo, non è difficile pensare che la matita sia uno di voi seduto su una sedia girevole. AB è un vostro braccio e MB è l’asse di una ruota di bicicletta D che ruota velocemente. Il sistema matita (persona + sedia) e disco rotante (ruota di bicicletta) è perfettamente stabile. Esso avrà un certo momento angolare, dato che vi è una rotazione. Voglio venirvi incontro. Il suo momento angolare è diretto verso l’alto ed è rappresentato dal vettore m. Esso vale Iw, dove I è il momento d’inerzia e w è la velocità di rotazione (vedi libri…). Tuttavia, non preoccupatevi più di tanto della formula e pensate solo a cosa capita praticamente.
A questo punto, facciamo un piccolo cambiamento alla configurazione precedente. Mantenendo sempre il disco (la ruota) in rotazione, ruotiamo l’asse MB di 180° rispetto a prima. Il disco continua a ruotare, ma -ovviamente- in senso contrario (l’ho ribaltato…). Il suo momento angolare è sempre m, ma con segno opposto, ossia diretto verso il basso, come indica la Fig. 1(b).
Tutto sembra di nuovo perfettamente stabile e in equilibrio. Ne siete veramente sicuri? Purtroppo no! Il momento angolare del disco ha cambiato di segno! Non si può permettere un cambiamento del genere senza colpo ferire. Perché? Ovvio: il momento angolare del sistema non si è assolutamente conservato, mentre invece doveva farlo! La figura non è quindi giusta. Manca qualcosa di veramente importante. Che cosa?
Potete anche farvi aiutare dall’esecuzione pratica dell’operazione (basta una sedia girevole e una ruota di bicicletta).
Aspetto una risposta abbastanza precisa… e non temete di lanciarvi: con voi non mi arrabbio di certo!
SOLUZIONE (leggete questa parte solo dopo avere cercato la soluzione da soli... se no che divertimento c'è?)
Il succo finale è la conservazione del momento angolare del sistema totale. Di esso fanno parte matita + braccio + ruota. Qualsiasi movimento venga fatto al suo interno (senza intrusioni di forze esterne), il momento angolare deve restare sempre lo stesso. Come qualcuno ha giustamente detto è qualcosa di simile al Sistema Solare dove devono giocare momenti angolari orbitali e momenti angolari di rotazione. Alla fine, se non arriva qualcosa da fuori rispetto al sistema solare che cambi il momento angolare, tutto ciò che capita al suo interno deve riportare il momento angolare finale al valore iniziale. Fortunatamente, nel caso trattato da questo articolo, la faccenda è molto più semplice.
Quali sono le condizioni di partenza? Un solo momento angolare applicato al sistema: la ruota che gira in senso antiorario. Il suo momento angolare m è, quindi, diretto verso l'alto. Ripeto: questa è la configurazione di partenza e questo è il momento angolare che devo conservare. Tutto il resto è immobile. Se, adesso, ribalto la ruota, ribalto anche il momento angolare che adesso diventa -m (la ruota gira in senso orario). Deve succedere qualcosa, dato che il momento angolare non si è conservato per niente: il suo verso è importantissimo perché inverte il senso di rotazione: la fisica deve intervenire. ATTENZIONE: il momento totale non deve cambiare perché non è arrivata nessuna forza dall'esterno del sistema a modificarlo. Il ribaltamento della ruota è stato fatto all'interno del sistema e quindi deve essere compensato. Se fosse arrivata una pallina da fuori, e avesse colpito la matita e/o la ruota, avrebbe cambiato completamente le cose, ma avrebbe anche cambiato il momento angolare totale.
Nel nostro caso, no. Abbiamo fatto tutto "in famiglia". Cosa bisogna allora introdurre per compensare il ribaltamento del momento angolare m? Facile, introdurre un momento angolare di segno opposto e di modulo doppio, ossia uguale a + 2m. A questo punto basta fare una somma di momenti angolari e verificare che si è tornati alle condizioni originali, ossia abbiamo conservato il momento angolare totale del sistema:
-m + 2m = +m esattamente come in Fig. 1(a)
Un momento angolare, però, deve essere applicato a qualcosa che è libera di ruotare. L'unica cosa che abbiamo è la matita che può girare su se stessa (ossia l'uomo che può girare con la sedia). Essa ovviamente si porta dietro tutto il sistema che è ancorato ad essa. Ed ecco quindi che ribaltando la ruota, la matita inizia a ruotare in senso antiorario portandosi dietro braccio e ruota (che continua a girare). Solo così si conserva il momento primitivo. La figura corretta è quindi la Fig. 2
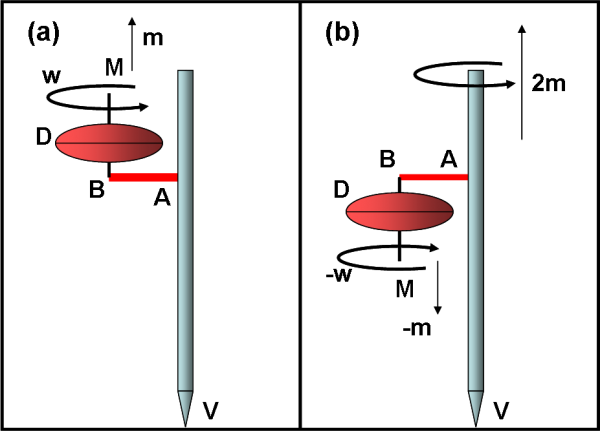
E se ribaltassi di nuovo la ruota? Ovvio... mi fermerei, dato che il momento angolare è tornato quello iniziale e la rotazione della matita non serve più.
Ha, però, anche ragione l'esperimento fatto da Giorgia. Se le condizioni iniziali fossero state ruota ferma e matita ferma, il momento angolare del sistema era nullo. Se metto in rotazione la ruota, introduco un m o un -m ( a seconda del verso) e quindi la matita inizia a girare in un verso o nell'altro in modo che:
m - m = 0 dato che 0 è la condizione iniziale, ossia il momento angolare totale originale.
Il momento angolare è una grandezza fisica fondamentale ed è l'equivalente della quantità di moto nei sistemi in rotazione. Come la quantità di moto è data dal prodotto della massa per la velocità, così il momento angolare è dato dal prodotto tra momento d'inerzia (legato alla massa) e velocità di rotazione.
P.S.: (per i più preparati): attenzione a non confondere momento di una forza con momento angolare introdotto da questa forza. Il momento di una forza è equivalente alla forza, mentre -ripeto- il momento angolare è equivalente alla quantità di moto. La forza non è altro che una quantità di moto che varia nel tempo in quanto varia la velocità. Il momento di una forza non è altro che il momento angolare che varia nel tempo, in quanto varia la velocità di rotazione. Non per niente, in fisica, abbiamo la conservazione della quantità di moto e la conservazione del momento angolare (se non intervengono forze esterne (o momenti di forze esterni) che fanno variare le velocità sia lineari che angolari).






59 commenti
Ciao Enzo,
bella domanda...?!?
Ammetto che per capire cosa succede realmente mi sono cimentata nell'esperimento e ho ripassato qualche nozione sul momento angolare ed ho avuto una bella sorpresa...
Facendo girare la ruota della bicicletta verso l'esterno ossia in senso antiorario mi sono accorta che io sulla sedia giravo in senso orario, capovolgendo la ruota ossia facendola girare in senso orario mi sono messa a girare in senso antiorario. Quindi questo vuol dire che su di me che sono seduta sulla sedia agisce una forza opposta a quella che è stata impressa alla ruota della bicicletta, dunque sulle figure dell'articolo mancano :
sulla figura a) una freccia/forza opposta a quella della ruota, che quindi punta verso il basso per la matita;
sulla figura b) una freccia/forza opposta a quella della ruota, che quindi punta verso l'alto per la matita.
è corretto?
Giorgia
Caro Enzo, Giorgia mi ha preceduto ed in modo sicuramente più puntuale di quanto volessi esprimere io. Effettivamente ti avrei detto che mancava una forza di senso opposto nelle due figure.
Adesso probabilmente sballo se parlo di forza centrifuga e/o centripeta.
Salve Sig. Vincenzo,
provo a dare la risposta,
nella figura a, la ruota gira in senso antiorario, quindi alla matita viene impressa una forza contraria che la fa girare con senso orario.
Nella figura b, la situazione si ribalta, in quanto la ruota gira in senso orario e la matita in senso antiorario.
se ho capito bene, quando la ruota viene ruotata di 180°, passa dalla posizione orizzontale ( quella dove gira in senso antiorario ) a quella verticale e dopo ritorna in posizione orizzontale ( questa volta girando in senso orario). Nel momento in cui la ruota si trova in posizione verticale, il momento angolare diciamo che si annulla per poi ripresentarsi non appena la ruota viene ruotata in posizione orizzontale....
Quindi nelle due figure, mancano le frecce che indicano il verso di rotazione della matita rispetto alla ruota.
Spero di non aver fatto troppa confusione
P.s.: ho formulato la mia risposta dopo aver visto questo video:
https://www.youtube.com/watch?v=UZlW1a63KZs
dove fa vedere come funziona il momento angolare, c'è anche l'esperimento con la ruota della bici...
cari Georgia e Mario,
non vi offenderete se lascio passare ancora un po' di tempo prima di rispondere per dare occasione di cimentarsi anche agli altri.
Mi fa piacere che vi siate accorti direttamente di qualcosa di apparentemente molto strano, ma vorrei che consideraste la situazione in un contesto fisico un po' più accurato...
Solo un piccolo aiuto...
Per rispondere esattamente... non pensate a possibili "forze", ma solo a ciò che appare... Considerate soltanto la situazione della parte (a) come quella di partenza : matita ferma e ruota che gira nel verso della figura . Cosa succede se ci portiamo nella posizione (b)? Un qualcosa che ci obbliga a fare qualcos'altro...
Vorrei che mi si dicesse non solo cosa succede, ma perché...
In altre parole, cosa vuol dire esattamente quella forza che pensate che manchi? E poi che forza è... e come può comparire dal nulla.
Basta... se no confondo invece di aiutare...
Enzo non dare la soluzione, oggi sono un pò impegnato e non riuscirò a rispondere prima di una certa ora
Enzo io ci provo, dato che dirò una sciocchezza non ti arrabbiare! J
La dinamica dovrebbe essere la seguente:
il momento angolare di un solo corpo in rotazione può avere il valore che vuole.
Nell’esempio però il sistema è costituito da due corpi.
In questo caso il momento angolare totale del sistema deve essere uguale a zero.
Negli articoli passati abbiamo sempre ragionato in termini di pianeti e satelliti e quindi di rotazione ed orbita
In questo caso non c’è nessuna orbita e quindi, per mantenere il momento angolare del sistema a zero, l’altro elemento deve avere un moto contrario rispetto al moto del segmento del nostro esempio.
Ovviamente invertendo il moto si invertirà anche il moto della matita.
Diverso sarebbe stato il caso di rotazione tra pianeti e satelliti.
In tal caso bisogna considerare anche il moto orbitale.
Nel caso in cui i due oggetti abbiano il moto di rotazione nello stesso verso, al cambiamento di verso del moto del segmento si otterebbe un aumento dell’orbita e un rallentamento della rotazione della matita/pianeta.
Nel caso di verso di rotazione inizialmente opposto, in caso di cambiamento del verso di rotazione del segmento ci sarebbe stato una riduzione di orbita.
caro Alexander,
come hai letto da SMA devo aspettare prima di dare la risposta...
Comunque voglio solo segnarti un punto ...
"In questo caso il momento angolare totale del sistema deve essere uguale a zero."
Perché???
Io sono partito dalla figura 1(a) dove la matita è ferma, ma ruota il disco. Questa è la nostra CONDIZIONE di partenza...
Scusate se batto su questo punto, ma è per rendere più facile la soluzione... fidatevi...
Caro Enzo mi viene profanamente (e vai, ho inventato qualcosa) da pensare, guardando la figura e esplorando un po' in giro, che il momento angolare si conserva grazie a quelle freccioline o forze che dir si voglia applicate al centro della ruota. La matita è ferma altrimenti ci dovrebbe essere uno scambio di momento angolare un po' come tra' un satellite ed il suo pianeta (Terra-Luna ?). Oddio mi stò addentrando in ragionamenti mai fatti prima e pericolosi...tutto questo grazie a te Enzo ede aituoi interessanti e stimolanti articoli.
Aiutooo!!!
Se la matita deve rimanere ferma allora mi viene da pensare che dato che la ruota è appesa ad una cerniera che ne permette il movimento libero, la ruota inizi ad oscillare su e giù e poichè durante il movimento la ruota perde energia, piano piano si fermerà.
Quindi la forza di rotazione che viene impressa alla ruota si trasforma nella forza di oscillazione che la fa muovere su e giù.
La forza può essere la forza cinetica dato che per definizione è una forza posseduta da un corpo grazie al suo movimento?
Giorgia
P.S:.:Forse ho fatto un po' di confusione...
fermi ragazzi... la cosa è più semplice di quanto non si pensi... e... non pensate alle forze!
Giorgia, non ti allontanare dall'inizio... non posso dire niente...ma...
Forse inizio a ruotare anche io, ossia la matita, perchè il momento angolare mi viene trasmesso dal disco in rotazione e si mantiene l'equilibrio. Pensa, pensa, pensa ...
Enzo, sbaglio a pensare che il "trucchetto" sta nella figura che "manca" tra la a e la b, cioé quando BM é allineato con AB? Personalmente mi sono chiesto cosa sarebbe successo a quel punto "intermedio" e mi sono cercato di dare la risposta per poi continuare fino alla situazione finale
mmm ... mi sembra complichiate una cosa molto più semplice... Non vorrei avervi confuso io con questo dire e non dire. Era meglio se stavo zitto.
Ricominciate da capo, senza tener conto dei miei vari commenti:
La domanda rimane questa: "cosa succede e perché succede, passando da (a) a (b)?". Da cui segue: "Cosa manca in (b) per renderla fisicamente corretta?".
Rileggete bene questa frase del testo:
Tutto sembra di nuovo perfettamente stabile e in equilibrio. Ne siete veramente sicuri? Purtroppo no! Il momento angolare del disco ha cambiato di segno! Non si può permettere un cambiamento del genere senza colpo ferire. Perché? Ovvio: il momento angolare del sistema non si è assolutamente conservato, mentre invece doveva farlo! La figura non è quindi giusta. Manca qualcosa di veramente importante. Che cosa?
La risposta è già lì... ma dovete ricordare cos'è il momento angolare...
Una bella freccia di verso m positivo(verso l'alto) che agisce sulla matita?
ehm...ehm... mi piacerebbe avere risposte che spieghino il come e il perché...
Per conservarsi , pur cambiando di segno, bisogna che sia stato redistribuito con segno + da un'altra parte? La matita inizia a muoversi?
Perché per tornare alla condizione di partenza di m é l'unico risultato possibile direi. Visto che la barretta AB non puo contribuire, l'unico "pezzo" del sistema che puo farlo é la matita, a cui viene quindi impressa una m positiva tale da ritornare alle condizioni di partenza.....Questo è il ragionamento che ho fatto, se é sbagliato chiedo scusa, ma sono in negozio e in tutta sinceritá il momento angolare ancora me lo devo studiare per bene
La ruota inizia a girare intorno alla matita diventando simile ad una trottola, e quindi la matita non cade a terra????
Spero con questa affermazione di non essere andata fuori dal seminato....
Giorgia
centra il giroscopio?
Perché il momento angolare si conservi nella seconda figura manca un momento 2m diretto in alto così che m = -m + 2m. Ho però difficoltà a capire a cosa sia applicato questo momento, ossia cosa si metta in movimento, se la sola matita o matita+ braccio...
Giornataccia lavorativa oggi... non ho avuto un secondo di riposo per fermarmi a riflettere... provo a buttare giù qualcosa prima di farmi una sospirata doccia rinfrescante
Il momento angolare del sistema persona/sedia + ruota bicicletta ha un suo momento angolare che deve rimanere costante. La persona/sedia è ferma (ma può ruotare) e la ruota gira. A questo punto varia il momento del sistema ruota, che passa da m a -m, per conservare il momento del sistema complessivo "persona/sedia + ruota bicicletta" la sedia dovrebbe ruotare (di 180°?) fino a trovare un nuovo equilibrio.
Allora concentriamoci:

Visto che ho sbagliato il primo tentativo ed enzo dice che la soluzione è semplice la butto li:
Per legge il momento angolare si conserva se non intervengono forze esterne.
Senza forze esterne quindi non sarebbe mai cambiato quindi nella figura manca il disegno della mia mano (similitudine di una forza esterna) che ruota l’asse MB di 180° .
In questo caso il momento non si è conservato.
Giusto?
Ps. credo che indipendentemente dal fatto se qualcuno riuscirà a risolvere il dilemma sarà necessario un nuovo articolo dedicato al momento angolare visto che è emerso che l'argomento (almeno per me) ancora non è chiaro!
Per poter passare dallo sato a allo stato b occorre poter imprimere una forza il cui effetto sta nel far girare il tutto attorno alla matita , la forza e data dalla forza centrifuga pertanto diminuisce la velocità di rotazione . Se l'asta A ad un certo punto si blocca sulla matita , la testa della matita assume un moto circolare che si amplia fino alla caduta della matita quando la forza centrifuga è 0 . Insomma direi che a b manca il segno della rotazione dell'asta intorno alla matita . La butto lì .
Aiuto ci provo Allora la forza data dal momento angolare indicata con la lettera m si somma alla forza di momento angolare della rotazione (centrifuga) almeno così mi sembra e il disco D salirebe in posizione parallela alla matita in pratica l'asse di rotazione sarebbe una linea retta formata dai punti A-B M Almeno credo
Comunque in parole povere nella figura manca la rotazione della matita intorno al proprio asse.
cari Tutti,
chi più chi meno ci siete andati abbastanza vicini. Il più vicino è stato sicuramente mmanzato, che si è solo posto una domanda finale inutile... dato che se gira la matita deve girare tutto il sistema che è a lei incernierato. Ricordate che ho parlato anche di uomo con un braccio che tiene un asse e quindi un uomo difficilmente può ruotare "a pezzi"...
Inoltre, il sistema non ha attriti e può ruotare indefinitamente come mostra la ruota.
Quindi... forse la cosa migliore è scrivere la soluzione nel testo in modo che sia maggiormente visibile.
Sì, manca un po' di comprensione del momento angolare dato che normalmente lo introduciamo come grandezza scalare (come numero), mentre invece è un vettore e il suo verso definisce il senso di rotazione... La forza agisce direttamente su un corpo e lo spinge nel verso della sua freccia. Il momento angolare è invece perpendicolare al moto di rotazione proprio perché deriva da un "prodotto vettoriale" tra forza e sua distanza dal punto al centro di gravità del sistema.
Questo esercizio mi serviva per parlare di momento angolare e della sua conservazione. Se pensate alle stelle di neutroni il discorso non cambia di molto: il momento angolare della stella che ruota è diretto verso il polo, dato che è questa la direzione perpendicolare al piano (medio) di rotazione di ogni particella della stella rispetto al suo baricentro, ossia il piano equatoriale...
In altre parole, il momento angolare di un oggetto in rotazione è diretto come l'asse di rotazione e il suo modulo (parte numerica) dà la sua intensità che è ripartita tra velocità angolare e momento d'inerzia (che dipende dalla massa e dalla distanza dall'asse di rotazione della parte più lontana del corpo in rotazione).
E' necessaria la lettura della Fisica addormentata... ma anche in quel caso ho agito senza derivate e quindi la trattazione è abbastanza contorta. Nessun problema... ci arriveremo presto! Vedete a quanto serve la matematica!
Tra non molto uscirà un articolo sul moto di precessione (decisamente più complicato) ma che verrà trattato in tre modi di difficoltà crescente. I momenti angolari diventeranno fondamentali. Inoltre sfateremo certe idee errate sull'effetto della Luna e la nutazione.
Bene a chi ha detto che questo "indovinello" si riferisce al giroscopio (e quindi alla precessione)...
Vado a scrivere la parte finale, così l'avrete quando vi svegliate...
ah ... dimenticavo: Georgia ha dato subito la soluzione giusta... ma non è riuscita a esprimerla in termini matematici e fisici. Tutto lì... ha parlato di forza e non di momento angolare e le cose sono diverse...
Enzo e se la matita non potesse ruotare come si comporterebbe il disco una volta ribaltato ?
Forse mi sono confuso guardando questo video.
http://www.youtube.com/watch?v=IEwAry0GARw
Grazie Enzo per la soluzione!

Che ci fosse la rotazione della matita non avevo dubbi, inizialmente ero propenso anch'io per una rotazione continua, poi m'è venuto in mente che si potesse fermare dopo mezzo giro dalla parte opposta
Quello che mi incuriosisce a questo punto é se davvero la matita gira a 2m(istintivamente sarei stato anche io per questa conclusione). Non dovremmo tenere anche in considerazione il moto di processione del disco? Grazie per l'ooportunitá di riflessione, Enzo.
@Foscoul,
se la matita fosse vincolata al pavimento, l'inversione della ruota cercherebbe di farla comunque ruotare, ma essa non potrebbe. Cosa vuol dire tutto ciò? Che noi applichiamo una forza alla matita che subisce dal pavimento una forza uguale e contraria. Il sistema subisce una forza esterna e il momento angolare è costretto a cambiare e non si conserva.
@ SMA,
sciocchezze... sono dubbi che vengono proprio perché si cerca di ragionare. L'importante è capire il meccanismo di base.
@Andrea
Se fai intervenire la precessione, vuole dire che si inserisce un ulteriore momento nel sistema e quindi la conservazione si adeguerà di conseguenza.
In ogni modo, direi che sono abbastanza contento di tutti voi... per ringraziarvi tra non molto vi BECCHERETE la precessione: Ahi... ahi ... ahi!!!

sono arrivato un po' in ritardo
ma:
@Vincenzo
se la matita fosse vincolata al pavimento, l’inversione della ruota cercherebbe di farla comunque ruotare, ma essa non potrebbe. Cosa vuol dire tutto ciò? Che noi applichiamo una forza alla matita che subisce dal pavimento una forza uguale e contraria. Il sistema subisce una forza esterna e il momento angolare è costretto a cambiare e non si conserva.
------------------------
Quindi mi viene da pensare che se la matita non può ruotare ci sarebbe una certa "resistenza" al ribaltamento della ruota.
Se ad esempio fossi seduto su una sedia fissa farei più fatica a ruotare perpendicolarmente al suo asse la ruota girante. Molto più che se se quest'ultima fosse ferma.
Come anche se nel punto B ci fosse uno snodo e facessimo liberamente cadere la ruota ruotante, il movimento di ribaltamento sarebbe più lento rispetto a quando non ruota.
Allora è proprio la conservazione del momento angolare che viene sfruttato per la stabilizzazione di certe attrezzature. Come ad esempio certe telecamere a cui vengono applicati dei giroscopi al fine di ridurre le vibrazioni ed i movimenti scattosi durante le riprese.
Ciao Enzo, abbi per favore pazienza con me ma come sai parto quasi da zero.
Quindi secondo te il concetto terra-terra di momento angolare è sintetizzato correttamente nel seguente modo?
In caso affermativo me lo appunto da qualche parte altrimenti chissà quante volte cadrò in incomprensioni! L
MOMENTO ANGOLARE
Il momento angolare è una grandezza fondamentale nella fisica e il suo valore numerico attesta la quantità di moto nei sistemi in rotazione.
Più correttamente però il momento angolare è un vettore determinato dal prodotto vettoriale tra il suo momento d’inerzia (legato alla massa e che in sintesi si può considerare come la quantità di forza necessaria da applicare al corpo per muoverlo) e la velocità di rotazione.
Proprio per questo il verso del vettore è sempre perpendicolare al piano di rotazione.
Il momento angolare totale di un sistema in rotazione costituito da più elementi è dato dalla somma algebrica dei momenti di ciascun elemento.
CONSERVAZIONE MOMENTO ANGOLARE
Se il sistema non è sottoposto a forse estranee al sistema stesso allora il momento angolare conserva sempre lo stesso valore iniziale.
In un sistema pianeta-satellite, alla riduzione di rotazione di un elemento deve necessariamente corrispondere un aumento dell’orbita e forse anche un aumento di rotazione dell’altro elemento.
Nell’esempio riportato, non essendoci l’orbita come elemento costitutivo del prodotto vettoriale, alla variazione di rotazione di un elemento deve per forza corrispondere una variazione di rotazione dell’altro elemento.
Ciao Enzo,
probabilmente la mia confusione deriva dal fatto che non ho trovato il tuo articolo pubblicato su astronomia.com sul momento angolare, mi sono informata per altre vie ed ho confuso un po' le cose... Beh, sbagliando si impara e adesso mi studierò bene il fenomeno in modo da essere più preparata per le prossime domande...
A presto
Giorgia
caro Carlo,
infatti, come aveva già accennato Giorgio, il sistema è molto simile a quello dei giroscopi...
caro Alexander,
un piccolo appunto qui:
MOMENTO ANGOLARE
Il momento angolare è una grandezza fondamentale nella fisica e il suo valore numerico indica la capacità di ruotare di un sistema.
Più correttamente però il momento angolare è un vettore determinato dal prodotto vettoriale tra il vettore posizione (rispetto al punto di rotazione) e il vettore quantità di moto (massa per velocità). Proprio per questo il verso del vettore è sempre perpendicolare al piano di rotazione. Il suo modulo può essere anche espresso come il prodotto tra il momento d’inerzia (legato alla massa e che in sintesi si può considerare come la resistenza di un corpo alla rotazione) e la velocità di rotazione.
Il resto va bene... Comunque, penso che sia meglio scrivere un articolo a riguardo... )
)
piano, piano ci facciamo anche la fisica... (ma varrebbe la pena leggere la Fisica addormentata, nel frattempo...
Alexander...
sarebbe anche meglio non dire "se non agiscono forse esterne", ma "se non agiscono momenti di forze esterne". Se una forza passa per il punto di rotazione non crea momento e non disturba il momento angolare...
caro Enzo, hai veramente ragione per quanto riguarda la fisica addormentata.

Sinceramente decisi di non comprarla perchè leggendo qualche commento qua e la mi era sembrata ampiamente oltre le mie possibilità.
Purtroppo più che una lettura per me dovrebbe diventare qualcosa di simile ad uno studio altrimenti come al solito inizialmente si pensa di aver capito tutto e poi dopo un mese alla prima domanda ti ritrovi in difficoltà.
Purtroppo il tempo è quello che è ma con un pò di organizzazione e centellinandolo ben bene forse forse...
Quasi quasi lo prendo!
Per tornare invece un attimo a noi, per verificare se ho capito (abbi pazienza se sono un pò petulante) vorrei variare leggermente l'esperimento e vedere che succede:
- se la matita è cementata al terreno ho ancora il problema della conservazione del momento al variare della rotazione del mio segmento?
Cerco di spiegarmi, mi sembra che la conservazione si abbia solo in un sistema in cui gli elementi che lo compongono son liberi di ruotare. Se la matita è bloccata non ho più un sistema rotatorio o sbaglio? In tal caso la natura non sarebbe piu costretta a conservare il momento
- se ad invertire la rotazione del segmento intervengo io che con la mano do una spinta opposta al senso di rotazione del segmento fisicamente applico, come mi sembrerebbe di aver intuito, un momento di forza esterna e quindi anche in questo caso verrebbe a decadere la legge della conservazione o sbaglio anche qua?
Se queste premesse non sono errate allora c'è una variazione della quantità di moto del sistema.
Dato che tu ci insegni che in natura nulla si crea e nulla si distrugge ma al massimo si trasforma, questa differenza di quantità di moto in che forma di energia si trasforma?
Sicuramente qualcosa che fa aumentare l'entropia totale...
Calore?
Ciao Alex provo a risponderti io:
1) No, perché la matita, non potendo ruotare, riceve una forza esterna al sistema (di uguale intensità, ma verso contrario) ed il momento angolare complessivo non è conservato (per sistema intendo "sedia/persona + ruota").
Il momento angolare si conserva solo se non intervengono forze esterne: pensa ad esempio ad una pattinatrice che ruota sul ghiaccio, portando le braccia al corpo ruota più velocemente (e il suo momento in questo modo è conservato). Ma se interviene uno spettatore dall'esterno e gli dà una bella spinta (quindi applica una forza esterna), il momento è violato e la poveretta si sfracellerà al suolo
2) E' in pratica quello che è successo nell'esperimento, in cui è variato il senso di rotazione della ruota. Visto che tu sei interno al sistema rotante, il momento complessivo si deve conservare, in quanto non viene applicata alcuna forza esterna. Questa tua spinta verrà compensata da una forza uguale e contraria ma all'interno del sistema, dunque il momento sarà conservato (un pò come la pattinatrice che muove le braccia mentre ruota).
Se invece tu sei esterno al sistema (forse è quello che intendevi) e quindi applichi una forza esterna ad esso, il momento angolare di questo non si conserverà.
Spero ovviamente di non aver detto delle cavolate!
che dire... SMA ha parlato come un libro stampato!!!! Non avrei potuto dire meglio... Sono veramente contento!!!! Un assistente prezioso veramente e-conoscendolo di persona- anche estremamente simpatico!
Posso solo aggiustare lievemente il tiro quando si parla di sistema in rotazione. Piuttosto che dire "agisce una forza esterna" è meglio dire "agisce un momento di una forza esterno". Sono piccolezze (anch'io mi sbaglio ogni tanto...), dato che è sempre una forza che fa intervenire un momento, se applicata a distanza dal centro del moto e in una direzione che non passa per esso. Nel caso della sedia ancorata al suolo, l'inversione della ruota causa un momento sul punto di contatto con il pavimento (qualcosa che vorrebbe far girare la sedia), ma a questa si oppone un momento esterno che lo fa sta stare fermo (causato dal vincolo sul pavimento). Il momento angolare non si conserva.
Per il resto grande SMA!!!
Caro Alexander, tu sollevi un problema generale:
Per descrivere momenti angolari, quantità di moto e prodotti vettoriali, è necessario fare discorsi zeppi di matematica. Ancora meglio sarebbe se si potessero usare le derivate, se no si rischia di complicare piuttosto che semplificare. Se si vuole restare nel semplice-semplice bisogna accettare alcuni risultati come dati di fatto. E' un serpente che si morde la coda... Ho cercato di pensare a un discorso sul momento angolare, ma per capirlo bene bisogna comprendere cosa vuol dire "variazione della quantità di moto" e, quindi, prima comprendere cosa sia la quantità di moto e le sue caratteristiche. Poi, una cosa è il vettore momento angolare e un'altra è il suo valore numerico, che può esprimersi in vari modi. E ognuno di essi indica solo uno scalare che non basta per definire un vettore. Ad esempio nel libro si definisce il momento angolare facendo variare la quantità di moto (senza ancora passare al prodotto vettoriale), ma poi si dimostra anche che esso corrisponde proprio alla quantità di moto in un sistema rotante. Parallelamente s'introduce il concetto di momento d'inerzia e di massa rotante... e via dicendo. Insomma, ogni descrizione è legata a qualcos'altro... E' praticamente impossibile affrontare un argomento di fisica da solo! Infine, per far variare il risultato di un prodotto vettoriale è necessario (per avere risultati numerici) saper derivare un prodotto e fare semplificazioni se i vettori sono paralleli... Solo così si potrà veramente dimostrare che l'introduzione di un momento di una forza esterno fa muovere il vettore momento angolare nella direzione del momento della forza.
Vi darò un piccolo esempio di come si può affrontare un problema classico di fisica a vari livelli: o si prende per buono e si accetta il concetto qualitativo o si è costretti a entrare nei dettagli matematici e bisogna legare tra loro molti concetti fino a scrivere per davvero un libro... Tra poco uscirà la precessione... anzi oggi stesso e mettetela nel cassetto e leggetevela con calma nei momenti di relativa tranquillità...
Sì, nella Fisica addormentata, ci sono molte formule, ma nessuna è lasciata senza spiegazione (dico bene SMA?). Bastano le nozioni di matematica più semplici, anche se vengono usate a raffica... Almeno credo che i veri problemi siano solo quelli...
Ragazzi miei, lezioni di matematica, di fisica, di meccanica celeste, ecc., ecc. mi riempirebbero il tempo fino al 2145! e tutto quel tempo non ce l'ho proprio...
Grazie mille a tutti e due, adesso comunque ho le idee più chiare anche se, come dice enzo, per capire veramente l’argomento è necessario conoscere la matematica e la fisica che ci sta dietro e che al momento sono ancora oltre il mio livello!
Comunque è un inizio, mi faccio un bel riassuntivo nel mio glossario personale cosi comincio a fissare qualche punto e visto che ci sono provo a vedere se mi viene fuori anche una definizione veloce veloce di quantità di moto e vettore!
Ciao Enzo è tutto merito della bontà del libro di Fisica, e di conseguenza del suo autore
Per il resto confermo quanto detto da Enzo, nella Fisica Addormentata ogni formula è spiegata dettagliatamente.
L'unico problema che si può incontrare è se si cerca di saltare un argomento per passare ad uno successivo (magari che riteniamo di maggior interesse). Ecco in questo modo si incontrano grosse difficoltà in quanto ogni spiegazione è strettamente legata alla precedente... in parole povere il libro va letto dall'inizio alla fine, ed in questo preciso ordine.
Sul prodotto vettoriale per me va bene così, mi pare di aver capito che andrebbero introdotti calcoli complessi che, dato il nostro livello (o perlomeno il mio), al momento eviterei accuratamente
caro SMA,
hai sicuramente ragione: l'ho proprio pensato come una favola scientifica... Non è certo un manuale da consultare, se non solo dopo averlo digerito...
Comunque, GRAZIE!!!!
Enzo scusa ma io sono un attimino indietro, ho l’impressione che ci sia qualcosa di importante che sbaglio sul momento angolare…
Ti faccio un esempio, cosa succede al momento angolare quando la nostra stella diventa una gigante?
Il momento si deve conservare.
Dato che il suo modulo è dato da L=I*w, anche se la massa rimane la stessa il sole aumenta di dimensione rispetto al suo centro e quindi dovrebbe diminuire la velocità di rotazione.
E’ corretto?
Il dubbio mi viene perché Il sole fa anche parte di un sistema composto da più elementi in rotazione.
A me sembrava di aver capito che il momento angolare del sistema era dato dalla somma dei momenti degli oggetti che ne facevano parte però mi sembra strano…
Dato che il sole, a fronte dell’aumento di dimensione e tramite la riduzione di rotazione avrebbe mantenuto costante il suo momento angolare, e dato che anche il sistema doveva per forza far rimanere costante il momento, ne conseguirebbe che anche gli altri pianeti dovevano mantenere costante il loro momento magari, in teoria, aumentando l’orbita e diminuendo la rotazione.
Escluso i cambiamenti sul moto di precessione che magari non saranno enormi sono quasi sicuro che dovrebbe succedere proprio quanto descritto sopra ma non capisco come si crea l’aumento di orbita e la riduzione di rotazione dei pianeti.
Infatti a rigor di logica il momento dei pianeti poteva conservarsi anche senza nessuna variazione di orbita e rotazione…
E’ colpa della marea o semplicemente ho equivocato il postulato che il momento angolare del sistema è dato dalla somma dei momenti angolari di tutti gli elementi?
No, Alexander, hai capito bene.
Devi, però, tener presente alcune cose:
posso sempre cambiare il sistema "chiuso".Ossia se prendo il Sole da solo, tutto ciò che va fuori di esso o arriva su di esso, deve essere considerato come momento o forza esterna e quindi fa cambiare il suo momento angolare. Se, invece, considero come sistema chiuso tutto il sistema solare, allora, qualsiasi cambiamento di momento angolare avvienga in un oggetto (Sole o pianeta che sia) deve essere compensato da qualche altra cosa, dato che le variazioni fanno parte del sistema. In questo caso il momento angolare completo deve conservarsi. Spero di essermi spiegato bene...
In questo contesto, devi pensare in grande. Quando il Sole diventa gigante, perde anche della massa e quindi il suo momento angolare non si conserva. Deve però conservarsi quello dell'intero sistema e quindi i pianeti dovranno modificare l'orbita. Però è anche vero che modificando l'orbita potremmo modificare anche la rotazione e allora deve cambiare qualche altra cosa pur di mantenere la somma di tutti i momenti angolari costante. Ogni pianeta, però, può essere considerato un sistema chiuso e quindi uno per uno subiranno un'effettiva variazione del momento angolare, in quanto ogni variazione deve essere considerata esterna.
In qualsiasi modo tu operi, però, i fenomeni che accadono devono rimanere gli stessi. Cambiano i singoli momenti angolari, ma la loro somma deve mantenersi. A meno che non arrivi qualcosa da fuori del sistema solare...
Nel caso che tu proponi: se non vi è perdita di massa, il Sole aumenta il raggio e quindi aumenta il momento d'inerzia e il momento deve conservarsi (niente è andato o è arrivato dall'esterno). A quel punto però, non è detto che la nuova struttura solare non alteri l'orbita dei pianeti e allora essi devono conservare il momento angolare complessivo: se uno si allontana, l'altro si avvicina e cose più o meno complicate... Rotazione e rivoluzione vanno di pari passo, dato che entrambe risentono di variazioni della situazione esterna. Il momento angolare del singolo pianeta può cambiare, ma non quello dell'insieme di tutti.
Spero di essere stato abbastanza chiaro... se no riproviamo...
Grazie sei stato chiaro anche se la situazione è un pò intrigata.

In pratica l'unico dato certo è che il sole manterrebbe il suo momento.
Potrebbe rischiare però, a causa delle sue mutate condizioni (stessa massa ma dimensioni maggiori e rotazione piu lenta), di influenzare i momenti angolari dei pianeti in quanto sarebbero sottoposti ad un momento di forza a loro esterno.
Il totale del momento angolare di tutto il sistema solare però deve essere comunque mantenuto dalla somma algebrica dei nuovi momenti dei pianeti.
In effetti non sono certo di aver capito bene però come dici tu, se uno non ha conoscenze di fisica e matematica, non ha la possibilità di apprendere in profondità certi argomenti quindi non vorrei nemmeno tediarti troppo su questo argomento.
L'interesse sul momento angolare mi era nato poche settimane fa da una tua risposta in cui mi riprendevi (in senso bonario) sul momento angolare di una stella che collassava in buco nero...
Provo a lanciarmi per vedere se finalmente ho inquadrato almeno in parte il fenomeno: prima di tutto avevo parlato di momento angolare rapportandolo alla velocità della luce confondendo in questo modo mele e pere.
Il momento angolare è un vettore dato dal prodotto del vettore posizione con il vettore quantità di moto e anche il suo semplice numero (modulo) non ha nulla a che vedere con la relatività ristretta.
Parlando invece di pura e semplice velocità di rotazione lungo l’asse dell’oggetto in contrazione (che quindi concorre solo in parte a determinare il vettore quantità di moto) mi sembrerebbe che questa sia ancora sottoposta ai vincoli della relatività ristretta e mi sembra di aver capito (ma sicuramente sbaglierò) che quando essa deve superare la velocità della luce, o in alternativa quando l’oggetto celeste entra dentro il suo orizzonte degli eventi, parte della velocità di rotazione viene “trasferita” allo spazio tempo circostante che a quel punto raggiunge una velocità di rotazione maggiore della luce proprio perché non sottoposto alla relatività ristretta.
Cosa succede al corpo celeste dentro l’orizzonte nessuno lo sa ma almeno nel mio universo non ho infranto la relatività ristretta…
Mi sono avvicinato almeno un pochino?
molto bene Alexander. Ogni cosa deve essere soggetta alla relatività sia ristretta che generale, dato che subentrano accelerazioni. Tuttavia, senza entrare in dettagli troppo complicati, direi che l'idea di base è corretta.
ciao tutti, manco da un pò (ho avuto una supplenza lunga, che fortuna !) ma questo vuol dire che ho cinque ore in meno al giorno che devo in qualche modo "far saltar fuori" e tra le varie cose ho dovuto rinunciare (momentaneamente...)al blog più interessante che esista . Ho visto che siete andati davvero avanti e io so che non ce la farò mai a rimettermi in pari A questa risposta sul momento angolare non sarei mai riuscita a rispondere. Adesso vado a vedermi un pò del resto anche se solo di corsa! (non dimenticatemi !!!!)
A questa risposta sul momento angolare non sarei mai riuscita a rispondere. Adesso vado a vedermi un pò del resto anche se solo di corsa! (non dimenticatemi !!!!)
ciao manuela,buon per te,d'altronde ora come ora avere troppo tempo libero non sarebbe un bel segno eh,anch'io non riesco a seguire tutto,c'è il lavoro e poi c'è enzo che è un fiume in piena inarrestabile,impossibile stargli dietro
Si anche io mi son ridotto alla pausa pranzo e la notte dopo le 11...

Comunque ben venga il piccolo sacrificio, è utile a 360 gradi stimolare la mente e la capacità deduttiva...
A mio avviso queste cose mi hanno anche aiutato ad affinare un approccio lavorativo più organizzato e razionale...
Quindi anche in questo caso grazie Enzo!
L'unico rischio grosso è quello di rimanere indietro a causa della non conoscienza di passaggi che enzo da per scontati, soprattutto in matematica.
Ancora mi ricordo quando qualche mese fa sbagliai il quadrato di un binomio, anche se non l'ho vista era come se ce l'avessi davanti la faccia basita di enzo!
Per limitare i rischi mi son trovato questo sito di matematica scuole medie-superiori a mio avviso molto utile per aiutarsi a risolvere piccoli-grandi dubbi:
http://matemedie.blogspot.it/
oppure
http://www.lezionidimatematica.net/index.htm
grazie dei links, utilissimi e graditissimi
puff...puff... Manuela...
mi avevi proprio spaventato! Che sollievo....
Sì, amici, avete proprio ragione sia per la mia eccessiva produttività sia per dare per scontato parte dell'algebra. Anche Giorgia ha dei problemi e quindi ho deciso di fare un riassunto delle cose fondamentali da ricordare (non le dimostreremo, ma tanto sono veramente facili e si può sempre fare se richiesto).
Riguardo alle troppe letture e al fatto di rimanere indietro, direi di fare così: invece di fare ogni mese un sommario completo degli articoli pubblicati, metterei solo le cose da non perdere. In modo che guardando lì uno sappia veramente cosa ha saltato di basilare e quanto è rimasto indietro. Per la matematica nessuna paura. Anche se vado avanti è facile recuperare tutti i capitoli e poi fare le domande in quello giusto. Chissà mai che alla fine, (seguendo i vostri consigli) non possa veramente fare un libro un po' speciale. Basterebbero una ventina di copie vendute per rifarmi delle spese di pubblicazione (molto dipende dal prezzo di copertina.. che potremmo decidere insieme)... Il problema è che non posso usare l'ebook della Feltrinelli perché non accetta molti simbolo matematici che per noi sono fondamentali.
Che dirvi... non ci riesco a stare fermo... forse saranno gli anni che avanzano e anch'io ho un limite per x che tende a qualcosa di sempre più vicino...
daiii che 68 anni sei ancora un ragazzino! pensa che con le leggi attuali lo stato ti avrebbe appena appena mandato in pensione!
forza che di libri ne puoi ancorascrivere a decine!
eh.... caro Ale la voglia c'è ma non basta.... io, comunque, ce la metto tutta e voi mi tenete giovane!!!
Beh, io non vorrei peccare di ottimismo (per quanto già una volta l'ho fatto, ricordi? con la fisica addormentata..) ma credo che, se venisse fuori un libro assemblando i vari articoli sulla matematica, altro che 20 copie.... E penso pure che pochi euro in più per poter coprire almeno le spese le si spenderebbe volentieri per avere in cambio un testo d'eccezione (fatto praticamente su misura e su ordinazione come certe scarpe ma di infinito valore in più) e spero con questo di non offendere nessuno, non vorrei che si pensasse che voglio fare i conti in tasca alla gente e decidere per gli altri.
Dico solo che uno che decide di comprarsi un buon testo di matematica (e non fatto su misura) sa già a che cifre va incontro. Pensa che in questi giorni sono in ballo proprio con un problema attinente a questo : mia figlia fa il liceo, abbiamo acquistato i libri di matematica indicati dalla scuola e sono un disastro: gli argomenti sono spiegati non solo in modo incomprensibile ma addirittura in un italiano scorretto (già : il libro è di matematica , mica di italiano...) e perfino una percentuale elevatissima di esercizi sono sbagliati, così i ragazzi perdono un sacco di tempo per risolvere un esercizio deprimendosi perchè si sentono idioti e il giorno dopo, a scuola, col professore, si scopre che l'esercizio era sbagliato. E stiamo parlando di libri di testo. Io, come rappresentante genitori nel Consiglio d'Istituto, ho la patata bollente : genitori e ragazzi protestano, la scuola deve trovare una soluzione e chi ha scelto questi testi? mah.... spero che il tuo eventuale libro potrà essere utilizzato anche da mia figlia...
cara Manu,
sei troppo buona! Sai, questa serie di lezioni , chiamiamole così..., sono costruite per fare arrivare in fretta a concetti come derivate e integrali. Va, quindi, di corsa, tralasciando molti argomenti che fanno parte dell'algebra e dell'analisi in genere. Tuttavia, se non proprio come testo per una scuola (sono perfettamente d'accordo con te sui testi odierni...), potrebbe servire come riassunto generale e/o per poter affrontare argomenti fisici con una certa base di conoscenza. Vediamo come viene, quali variazioni o aggiunte o tagli penseremo di fare tutti assieme, e poi perché no? Magari verrebbe utile a qualche insegnante per capire meglio certi concetti che dovrebbe spiegare ai giovani...
Più che altro è essenziale lo spirito e la passione con cui si insegna...
A me sono rimaste negli anni solo le materie e i concetti spiegati da chi aveva passione per l'argomento...
Heheheheh! Arrivo tardi anche qui, ma il giochino già lo conoscevo ;)
Il meccanismo dovrebbe essere lo stesso che permette anche ai satelliti artificiali di rimanere stabili ed, all'occorrenza, di poter temporaneamente ruotare per cambiare il proprio puntamento; dovrebbe essere utilizzato anche dalle sonde spaziali e dai telescopi Hubble e Kepler (quest'ultimo ha avuto recentemente un guasto proprio ad uno di questi dispositivi)... diciamo, più in generale, da qualsiasi dispositivo artificiale mandato nello spazio.
Ciao,
Alex.