Questo articolo è stato inserito nella sezione d'archivio "Sistema Solare"

 

Un piccolo passatempo per Natale, sfruttando le risposte al quiz sul moto del Sole. Anzi, non vi do nemmeno le risposte (troppo fredde e banali), ma la descrizione di come sia estremamente semplice rispondere sia a loro che a molte altre. Il Sole (geometricamente) non avrà più segreti. Per qualcuno sarà un’ovvietà ma, al limite, può sempre illustrarla ai bambini.

Avrei potuto rispondere alle domande e controllare le risposte. Avrei anche potuto dare solo le risposte e poi ognuno poteva controllare. Avrei anche potuto chiedere scusa delle domande, molto “cattive”, 3 e 4. Pensateci bene e le risposte sono veramente molto subdole e -a prima vista- maligne, facendo capire una cosa che invece non c’entra per niente.

In realtà volevo solo tastare il polso ai miei amici e capire se valeva la pena di fare un discorso più generale di come si vede il Sole nelle varie zone del nostro pianeta. Penso di sì, dato che, a parte la 3 e la 4, le altre hanno avuto risposte generalmente corrette. Tuttavia, sapete come sono fatto: vorrei non solo che certe cose si sappiano, ma anche che si derivino in modo semplice e generale. Oltretutto stiamo parlando di matematica e di geometria. Perché non approfittarne e scrivere un articolo generale che può permettere, con una sola figura di base, di trovare tutto ciò che volete con le vostre sole forze e, penso, in modo molto divertente? Prendetelo come REGALO DI NATALE, anche perché, chi ne ha voglia, potrà divertirsi a fare altri esempi e sbizzarrirsi. Soprattutto essere sempre pronto a mostrare ad altri come il tutto sia estremamente semplice e intuitivo.

Dopo aver digerito l’articolo e le sue numerose figure, potrete tornare alle domande e le vedrete sotto occhi in parte diversi. Se qualcuno aveva giù usato il sistema geometrico che sto per prospettarvi, mi scusi… e pensi che per molti altri potrebbe essere proprio una specie di nuovo gioco o passatempo.

Iniziamo col definire i due sistemi di riferimento che ci interessano quando parliamo di altezza e movimento di un astro sulla sfera celeste per qualsiasi luogo della Terra.

Uno è formato sicuramente dall’orizzonte e dalla sua perpendicolare che indica lo zenit (la direzione del filo a piombo). Questo sistema varia da luogo a luogo: ognuno ha il suo orizzonte.

Il secondo sistema è quello che vede come piano di riferimento l’equatore e la sua perpendicolare che individua i Poli Nord e Sud. Questo è un sistema fisso che possiamo trasportare in ogni luogo della Terra, ma che rimane sempre lo stesso. Operiamo solo una traslazione di assi (tanto per non dimenticarci delle funzioni…).

In ogni punto del globo è facile individuare questi due sistemi di riferimento. E’ inutile fare disegni in tre dimensioni che portano sempre a complicazioni. Limitiamoci al piano del foglio che rappresenta il meridiano del luogo, ossia il piano che contiene sia lo zenit che i poli. E’ proprio quello in cui qualsiasi stella ha la sua culminazione superiore (e inferiore), ossia dove raggiunge il punto più alto (e il più basso, che a noi interessa poco).

Diamo alcune definizioni: si chiama latitudine φ del luogo l’angolo al centro della Terra C tra l’equatore EE e la direzione del punto sulla superficie P. Questa direzione è proprio quella che indica lo zenit del luogo. L’orizzonte è la perpendicolare alla direzione dello zenit passante per il punto, ossia è la tangente alla Terra nel punto scelto. L’angolo tra l’orizzonte e un astro si chiama altezza sull’orizzonte. Se l’astro si trova proprio nella direzione dello zenit la sua altezza è 90°, mentre diventa 0° se l’astro sta sorgendo o tramontando. Vediamo tutto ciò nella Fig. 1, la base di tutto la nostra chiacchierata.

L’altezza è stata indicata con h. L’angolo tra equatore e astro S si chiama declinazione δ dell’astro. Nel caso delle stelle (meno una… la nostra) essa è un valore fisso che varia leggermente nel tempo (precessione e cose del genere), ma che per il nostro “gioco” può essere considerata una costante che individua la stella nel cielo al suo passaggio al meridiano (ma anche prima e dopo attraverso un  po’ di trigonometria sferica).

Ho parlato di stelle solo per farvi capire che tutto ciò che diremo è applicabile a tutti gli astri del cielo. Anzi, decisamente più semplice proprio per la costanza della declinazione durante tutto l’anno e per qualsiasi luogo della Terra (ecco un giochino che potreste fare… disegnare alcune stelle e vederne la loro altezza in punti diversi del globo, conoscendo -ovviamente- la sua declinazione che si trova in molti cataloghi o siti web). E, poi, potreste anche vedere quanto resta visibile durante certe notti.

Comunque, soprassediamo e pensiamo a una stella veramente speciale: il Sole. In fondo non è diversa dalle altre, tranne per il fatto che gira intorno a noi (eh sì… ci conviene tornare alla visione pre-copernicana… anche perché c’interessa solo ciò che vediamo, immaginandoci fermi nello spazio) lungo un’orbita che giace su un piano diverso da quello dell’equatore. Ne segue che la declinazione del Sole cambia durante l’anno (una stella molto vivace).

Fortunatamente sappiamo bene quali sono i suoi valori massimi e minimi, dato che conosciamo l’angolo che il suo piano (eclittica) fa con l’equatore (circa 23°).  La declinazione del Sole passa, quindi,  proprio da + 23° a 0° a -23° ancora a 0° e infine di nuovo a + 23°. Sono i punti che noi abbiamo associato ai famosi solstizi ed equinozi… In particolare, quando il Sole ha una declinazione uguale a + 23° siamo al solstizio d’Estate, Poi tocca lo zero e siamo agli equinozi, a -23° siamo al solstizio d’Inverno. Ve bene… sia come sia, sappiamo come disegnare la direzione della stella Sole nella Fig. 1 per certi giorni dell’anno nel suo momento di passaggio al meridiano (il punto più alto). Chiamiamo il valore massimo della declinazione solare ε, che sappiamo valere 23°.

Spostiamoci, allora, nella Fig. 2, che cerchiamo di usare per passare da una semplice geometria a un formula matematica che permetta di ricavare sempre l’altezza del Sole S, qualsiasi sia il luogo prescelto, in funzione della declinazione δ_S del Sole (ossia dei diversi giorni dell’anno).

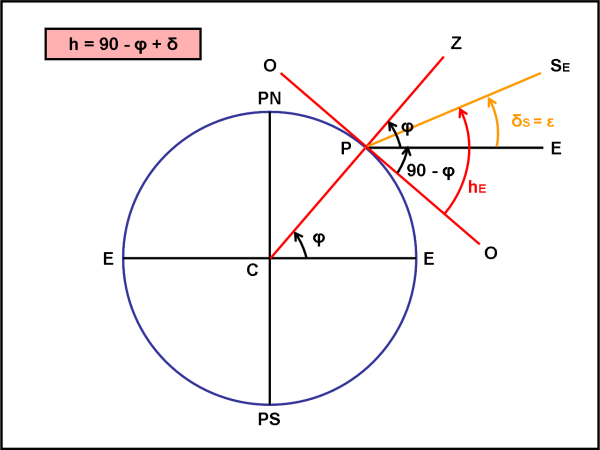
Cominciamo con una qualsiasi declinazione del Sole (abbiamo scelto una declinazione uguale proprio a +23° per risparmiare una figura…) e cerchiamo di legare insieme ciò che sappiamo con quello che vogliamo trovare. L’incognita è l’angolo h, gli angoli noti sono invece la latitudine φ del luogo e la declinazione del Sole δ_S. L’angolo ZPE è per definizione la latitudine φ. L’angolo EPO è allora uguale a 90° – φ, dato che OPZ è retto, per costruzione. EPS è uguale alla declinazione del Sole δ_S (che, ripeto, in questo caso vale proprio + ε , ma potrebbe assumere tutti i valori tra + ε e – ε al variare del giorno dell’anno). L’angolo OPS è l’altezza h da determinare e quindi dobbiamo scriverla in funzione degli altri due angoli. E’ semplicissimo ricavare che la formula generale vale:

h = 90° – φ +  δ_S   …. (1)

Nel caso della figura si ha:

h_E = 90° – φ +  ε     (altezza del Sole al solstizio d’Estate)

 

La formula (1) vale per tutte le posizioni del punto P e per tutte le posizioni del Sole S. La situazione descritta nella Fig. 2 è proprio quella relativa al solstizio d’Estate, dato che il Sole S_E si trova alla sua massima declinazione positiva (ε). Ovviamente cambiando giorno dell’anno cambia la declinazione del Sole.

Passiamo alla Fig. 3, in cui consideriamo la situazione durante gli equinozi, ossia quando S_AP = 0°.

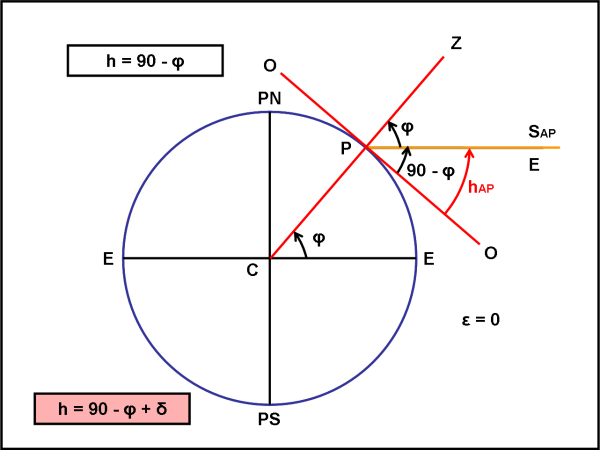
Gli angolo della figura ci permettono nuovamente di ricavare graficamente l’altezza del Sole, tenendo conto che adesso δ_S = S_AP = 0° (direzione del Sole coincidente con l’equatore, per definizione di equinozi). Otteniamo, però, lo stesso risultato, matematicamente, ponendo δ_S = 0° nella (1). In conclusione si ha (graficamente o matematicamente):

h_AP = 90° – φ        (altezza del Sole agli equinozi d’autunno e primavera)

Infine portiamoci al solstizio d’Inverno (Fig. 4), dove δ_S = S_I = - ε. Sia graficamente che matematicamente si ha che:

h_I = 90° - φ - ε     (altezza del Sole al solstizio d’Inverno)

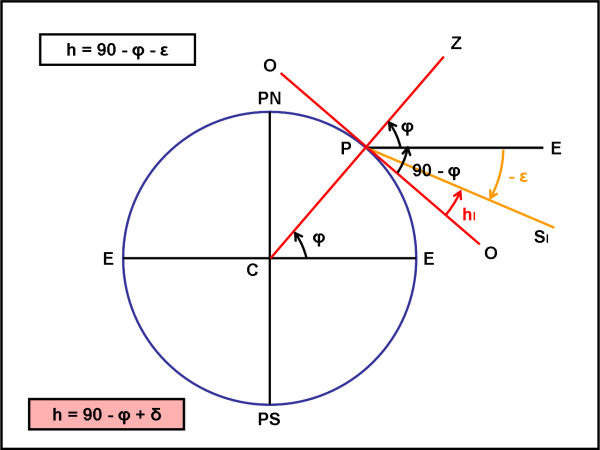
Cosa possiamo concludere? Che nel luogo P di latitudine φ l’altezza del Sole al passaggio al meridiano (mezzogiorno) varia da un massimo di 90° – φ +  ε  a un minimo di 90° - φ – ε.  Facciamo un esempio? Prendiamo un luogo a 42° di latitudine nord. ε sappiamo che vale 23°, ne segue che:

71° < h_S < 25°     (variazione dell’altezza del Sole al meridiano per un luogo di latitudine 42°)

Divertitevi a trovare questo intervallo per tutti i luoghi che volete e magari anche per declinazioni del Sole intermedie.

Potrei anche finire qui l’articolo, perché avete in mano tutti i dati per risolvere ogni caso. Visto che siamo quasi a Natale, sarò buono e disegno anche quattro casi particolari, molto interessanti.

Via allora con la Fig. 5 che si riferisce al Polo Nord.

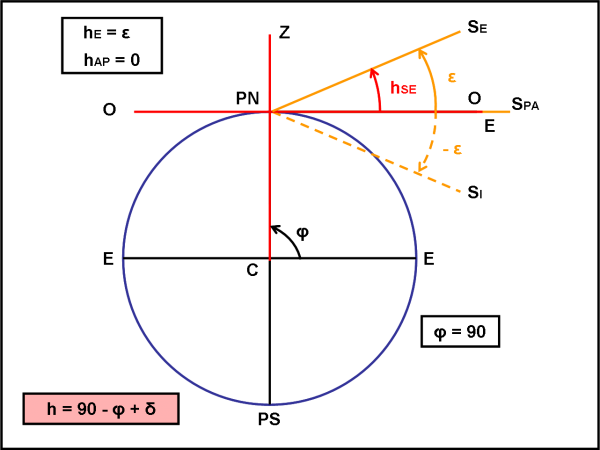
Disegniamo subito l’orizzonte e lo zenit del luogo. Per non farla troppo lunga, inseriamo nella stessa figura le tre posizioni peculiari del Sole (solstizi ed equinozi).  Le cose si semplificano di molto dato che φ = 90°. La (1) diventa quindi soltanto:

h_S = δ_S

E nei soliti giorni peculiari dell’anno:

h_E = ε       (solstizio d’Estate)

h_AP = 0     (equinozi)

h_I = - ε      (solstizio d’Inverno)

Come si possono tradurre a parole?

Al solstizio d’estate il Sole raggiunge la sua massima altezza che è proprio uguale a 23°. Nei gironi degli equinozi il Sole arriva solo all’orizzonte (teoricamente se ne vede solo metà). Al solstizio d’inverno raggiunge un’altezza negativa e quindi non si può vedere.

Non chiedetevi, adesso, che percorso fa il Sole durante il giorno, dato che ci torneremo più tardi usando la stessa figura base.

Scendiamo verso Sud e fermiamoci in un punto che ha latitudine  67°. Perché ho scelto proprio questo punto? Perché 67° è l’angolo complementare di 23° = ε. In altre parole: 67° = 90° - ε. Questa situazione è estremamente importante. Disegniamo la Fig. 6.

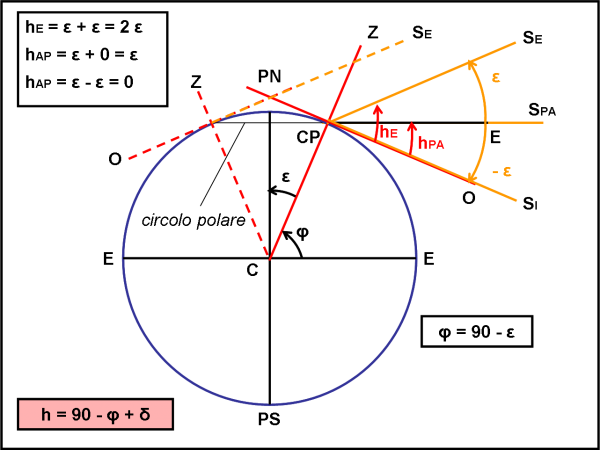
Scegliete il modo che preferite, fatto sta che l’equazione (1), diventa:

h_S = 90° - 90° + ε +  δ_S = ε +  δ_S

e nei soliti giorni:

h_E = ε + ε = 2ε     (solstizio d’Estate)

h_AP = ε + 0 = ε     (equinozi)

h_E = ε - ε = 0        (solstizio d’Inverno)

Tradotto a parole: al solstizio d’estate il Sole arriva a un altezza massima di 2ε = 46°. Agli equinozi l’altezza diventa proprio 23°. Al solstizio d’inverno il Sole ha un altezza uguale proprio a zero. In quel giorno e solo in quel giorno il Sole non sorge!

Siamo esattamente sul circolo polare artico. Notate che se faccio ruotare la Terra di 180°, ossia mi porto alla mezzanotte del luogo, l’altezza del Sole, al solstizio d’Estate (e solo in quel giorno), scende solo fino a 0°, ossia non tramonta.

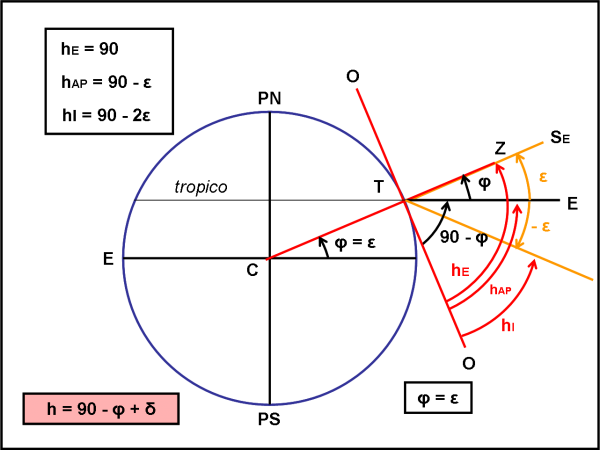
Passiamo alla Fig. 7, dove la latitudine del luogo è proprio uguale a ε. La nostra formula generale (1) diventa:

h_S = 90° - φ + δ_S  =  90° - ε + δ_S

Nelle date particolari si ha, quindi:

h_E = 90° - ε + ε = 90°      (solstizio d’Estate)

h_AP = 90° - ε                    (equinozi)

h_I = 90° - ε - ε = 90° - 2ε       (solstizio d’Inverno)

Ci troviamo sul tropico del Cancro e il giorno del solstizio d’estate il Sole raggiunge esattamente lo Zenit. Nel solstizio d’inverno raggiunge, invece, l’altezza minima di 90° – 46° = 44°.

Concludiamo questa prima parte, portandoci sull’Equatore, ossia in un punto che ha φ = 0° (Fig. 8).

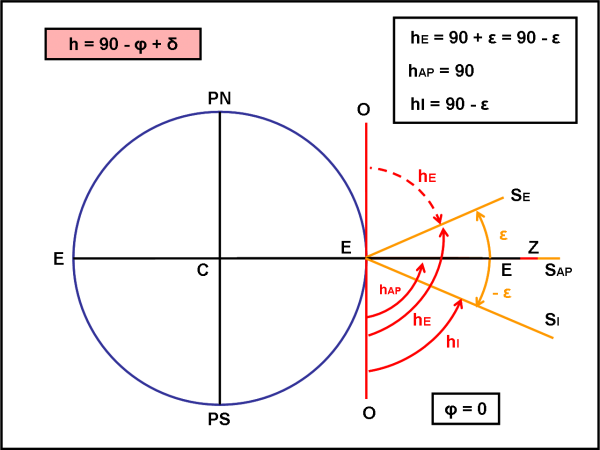
La solita formula base (1) si trasforma in:

h_S = 90° + δ_S

e quindi

h_E = 90° + ε            (solstizio d’Estate)

h_AP = 90°                (equinozi)

h_I = 90° - ε             (solstizio d’Inverno)

Notiamo che l’altezza al solstizio d’estate è maggiore di 90°. Questo ha poco significato, dato che l’altezza può raggiungere solo 90°, ossia lo zenit. Per trovare la vera altezza, basta prendere l’angolo supplementare a h_E, ossia 180° – h_E = 180° – 90° – ε = 90° - ε . L’altezza al solstizio d’estate è uguale a quella del solstizio d’inverno. Questo risultato era prevedibile, data la simmetria tra le due configurazioni.

All’equatore il Sole raggiunge lo zenit due volte all’anno (equinozi) e si sposta da un alto a dall’altro (solstizi) scendendo non oltre i 67°.

Notate che la differenza tra le altezze del Sole è sempre uguale a 2ε = 46°, cosa che graficamente non può certo stupirci. Ogni tanto quest’angolo ci è venuto 44 e altre volte 46, ma ciò è dovuto al fatto che abbiamo preso ε = 23, senza tenere conto dei … rotti. Se volete fare dei calcoli esatti considerate, più esattamente:

ε = 23.439281°

Non era certo difficile calcolare la differenza di altezza del Sole, costante per tutti i luoghi della Terra. Bastava fare h_E – h_I e il risultato sarebbe stato 2ε indipendentemente dal punto prescelto… La matematica risponde sempre facilmente. Nel caso dell’Equatore, per trovare la differenza di altezze si dovrebbe proprio prendere il valore maggiore di 90°.

La Fig. 1, usata come base per tutti i casi particolari, può ancora venirci molto utile per  determinare il rapporto tra la durata del giorno e della notte. E’ veramente uno scrigno di informazioni!

Consideriamo il caso generico descritto dalle Fig. 2,3 e 4 e riproposto, in modo semplificato, nella Fig. 9. Ho eliminato scritte e angoli vari, lasciando solo il punto e le tre direzioni del Sole, oltre che orizzonte, direzione dello zenit ed equatore.

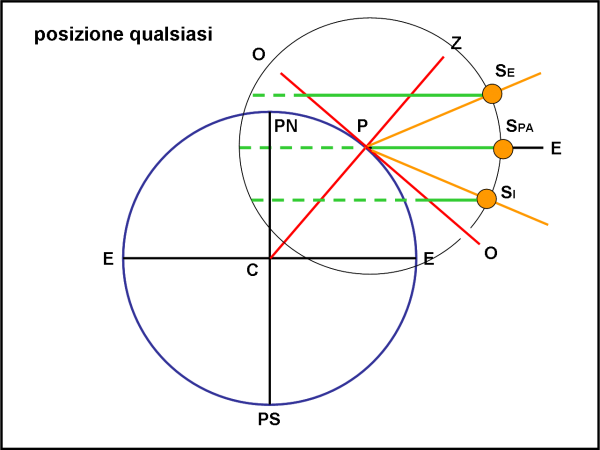
E’ facile, inoltre, costruire attorno al punto P la sua sfera celeste. Qualsiasi diametro va, ovviamente, bene. Segniamo su di essa le tre proiezioni del Sole. Qual è il percorso della nostra stella durante l’arco di un giorno? Facilissimo: lei si muove descrivendo un cerchio parallelo all’equatore. Nella figura, vista di profilo, il cerchio descritto dal Sole sarà la corda parallela alla linea dell’equatore del luogo, ossia la linea verde (tre, perché consideriamo il movimento ai due solstizi e agli equinozi). La parte sopra l’orizzonte del luogo è disegnata continua e si riferisce al periodo diurno. Quella tratteggiata alla parte notturna, quando il Sole è sotto l’orizzonte.  La conoscenza dell’altezza e della durata relativa al tratto diurno ci dà tutte le informazioni richieste.

Disegniamo la stessa figura per tutti i casi particolari descritti precedentemente. La linea verde relativa agli equinozi sarà sempre metà tratteggiata e metà continua, dato che in questi giorni dell’anno i due percorsi (notturni e diurni) devono sempre essere uguali in qualsiasi punto della Terra. Al solstizio d’Estate prevale la parte diurna e a quello d’Inverno la parte notturna.

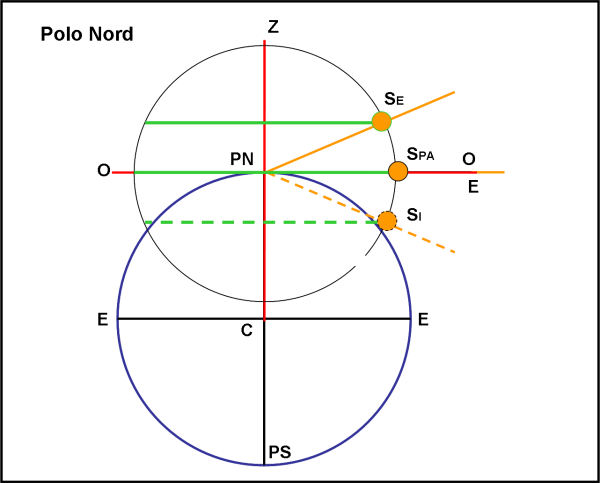
Commentiamole brevemente. La Fig. 10 si riferisce al Polo Nord. Al solstizio d’Estate il Sole descrive un cerchio parallelo all’orizzonte ad un’altezza di 23°, come sappiamo molto bene. Il cerchio coincide proprio con l’orizzonte agli equinozi e diventa completamente notturno al solstizio d’Inverno.

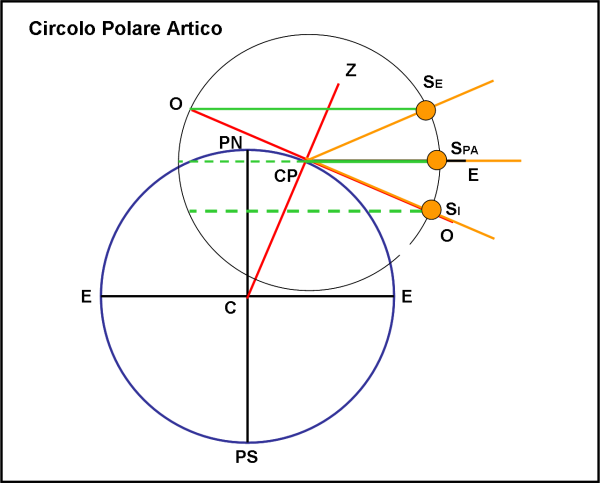
La Fig. 11 si riferisce a un punto sul circolo polare artico. Al solstizio d’Estate il percorso del Sole è completamente diurno e arriva a toccare l’orizzonte a mezzanotte (il celebre Sole di mezzanotte). Agli equinozi si ha la solita situazione intermedia, mentre al solstizio d’Inverno il percorso è sempre notturno tranne un punto a mezzogiorno. Tra Polo Nord e circolo polare artico abbiamo tutte le configurazioni intermedie (facilmente tracciabili) con una durata sempre maggiore delle giornate senza notte e di quelle senza Sole. E’ facilissimo mettere in pratica quello che abbiamo imparato!

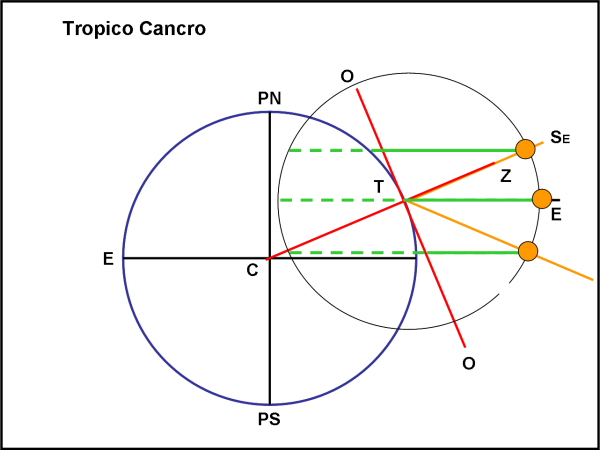
Continuiamo con la Fig. 12, ossia con la situazione al tropico del Cancro. C’è poco da dire, ma si nota bene come la durata della fase diurna è sempre piuttosto lunga e relativamente poco diversa da quella notturna. Il Sole cade quasi verticalmente verso la linea dell’orizzonte e sparisce in fretta, così come sorge altrettanto velocemente.

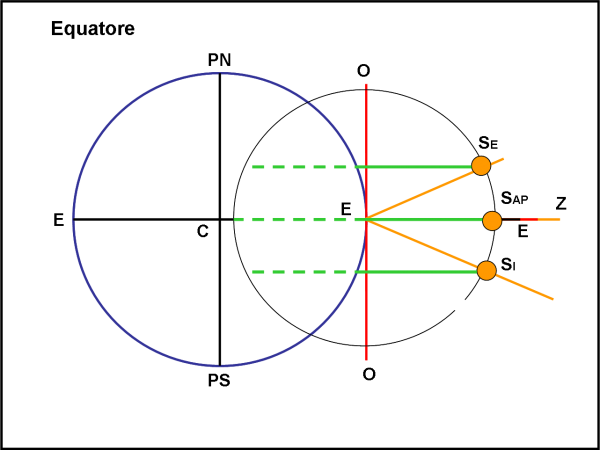
Situazione non molto diversa capita all’equatore (Fig. 13), con la differenza più grande nel fatto che la traiettoria del Sole è sempre perpendicolare alla linea dell’orizzonte. Il Sole sorge e tramonta secondo un angolo di 90° rispetto all’orizzonte: sembra proprio un missile, ve lo assicuro!

Divertente, vero? E’ il tutto l’abbiamo ottenuto con una semplicissima figura in due dimensioni.

Concludo con due inviti:

1)      Disegnate da soli le configurazioni dell’emisfero Sud. Non solo è facilissimo, ma troverete le stesse configurazioni ribaltate.

2)      Ripensate bene alle domande che vi ho fatto e vedrete che risponderete in modo diverso… soprattutto alle 3 e 4 (veramente cattive e prive di senso… scusate ancora…).

Buon divertimento e BUON NATALE a tutti!