Volevo solo “sfiorare” le coniche, considerandole come altre funzioni che impareremo a studiare nei dettagli. Tuttavia, la loro enorme importanza mi ha bloccato e convinto che meritano qualcosa di più. L’articolo è diventato chilometrico, per cui lo divido in cinque parti. Non solo matematica, ma anche tanta geometria. Cominciamo… affettando un cono con un coltello molto affilato.

Uno cono spaziale

Parlare delle coniche necessiterebbe di libri interi. Non solo per la loro importanza fondamentale legata al moto dei corpi celesti sottoposti alla forza di gravità, ma anche per i vari modi con cui si possono introdurre. Vi è solo l’imbarazzo della scelta. Per lo scopo di queste “lezioni”(chiamiamole un po’ enfaticamente così) ci basterebbe una trattazione sotto la veste di polinomi (vi ricordate?) di secondo grado. Tuttavia, mi sembrerebbe un omicidio non spiegare il loro nome e le peculiarità geometriche che le rendono oltremodo simpatiche.

Perché si chiamano coniche? Tutto parte effettivamente da un cono. Attenzione, non il cono come corpo solido che si disegna a scuola, ma come cono in senso generale, di cui quello dei problemi di geometria delle scuole medie è un caso molto particolare. Ormai sappiamo cos’è una retta e sappiamo anche descriverne la funzione. Teoricamente questo ci permetterebbe di passare da una trattazione puramente geometrica a una trattazione matematica. Dovremmo, però, saper scrivere le equazioni delle superfici nello spazio e delle loro intersezioni. Insomma, un lavoraccio che esula dai limiti di questa nostra “fatica”. Consideriamo quindi la retta come linea geometrica, senza pensare alla sua rappresentazione matematica. Qualcuno dirà: “Meno male!”. Forse sì e forse no…  Poi mi direte…

Disegniamo nello spazio a tre dimensioni una retta verticale, come rappresentato nella Fig. 37.

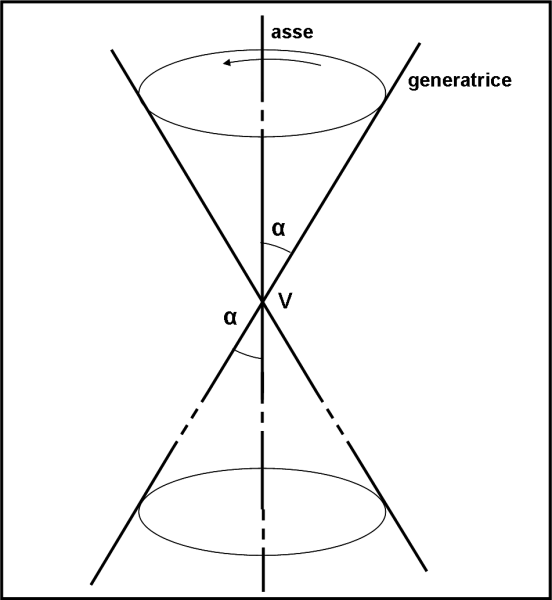
Questa retta chiamiamola asse a. Adesso, ne prendiamo un’altra, r, (generatrice), inclinata di un certo angolo rispetto a lei (ad esempio α). Chiamiamo V il punto della loro intersezione. Bene, il più è fatto. Ora abbiamo due strade da percorrere: o disegniamo “infinite” rette (infinite vuol dire quante ne vogliamo, una attaccata all’altra) che formino tutte lo stesso angolo con l’asse e che passino  per V, oppure, più facilmente, facciamo ruotare la retta r intorno all’asse a (mantenendo costante l’angolo α), imponendogli di lasciare un chiaro segno di dove passi, ossia di descrivere una superficie continua. In un modo o nell’altro si ottiene un cono! Troverete molte altre definizioni a riguardo, ma a noi bastano e avanzano queste due.

Prima di procedere, alcune considerazioni su questa superficie che abbiamo costruito. Innanzitutto, la più importante: non è un cono qualsiasi, ma un cono circolare. Ossia se lo tagliassimo con un piano qualsiasi,  perpendicolare, all’asse otterremmo delle circonferenze, che hanno come centro il punto corrispondente sull’asse. Questo risultato è ovvio, dato che abbiamo fatto ruotare la direttrice attorno all’asse mantenendo l’angolo α costante. Avremmo potuto, invece, farlo cambiare in qualche modo e poi tornare a quello iniziale e avremmo potuto ottenere coni con sezioni più o meno strane. Noi, comunque, siamo interessati a quello circolare: è il più semplice, ma è già più che sufficiente.

Per non creare confusioni inutili, due parole sul tipico cono che si impara a scuola e di cui si calcola volume, superficie e cose del genere. Per ottenerlo, basta prendere un triangolo rettangolo e farlo ruotare attorno a un cateto. Otterremmo un solido, dato che il triangolo ha una sua area, la cui superficie esterna è una piccola parte di un cono generale, come quello descritto precedentemente. Ci servirebbe quel piccolo solido di dimensioni limitate? Per alcuni casi, forse sì, ma per altri assolutamente no. Ricordiamoci, infatti, che vogliamo ricavare delle funzioni, delle linee che potrebbero anche andare all’infinito. Un piccolo triangolo finito non potrebbe dirci niente su una parola, per lui, incomprensibile, come infinito. Il cono che abbiamo introdotto noi è, invece, una superficie che non ha un confine, dato che è formato da rette che, per la loro stessa definizione, vanno all'infinito sia da un lato che dall’altro.

Un coltello e … affettiamo il cono

Fissate queste semplici considerazioni, non ci resta che andare a prendere un coltello con una lama sottilissima e tagliente. Immaginiamo che abbia la forma di un piano, in modo da avere a disposizione un’estensione illimitata. Cominciamo, allora, ad affettare il nostro cono. Iniziamo con il modo più semplice, illustrato in Fig. 38. Teniamo il piano-coltello perpendicolare all’asse a. Cosa otteniamo? Beh, già l’abbiamo già visto quando abbiamo definito il cono come circolare. Tante circonferenze con i loro centri che percorrono proprio l’asse a. Ve n’è uno molto particolare: quello che passa proprio per V. L’intersezione con il cono diventa un punto, proprio V. La circonferenza degenera in un punto.

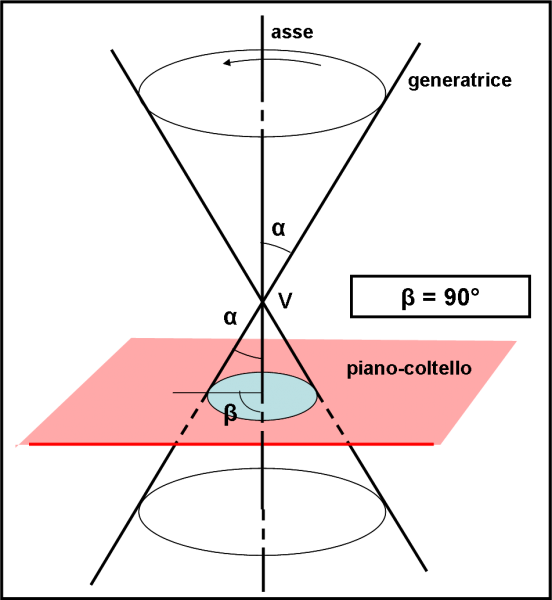
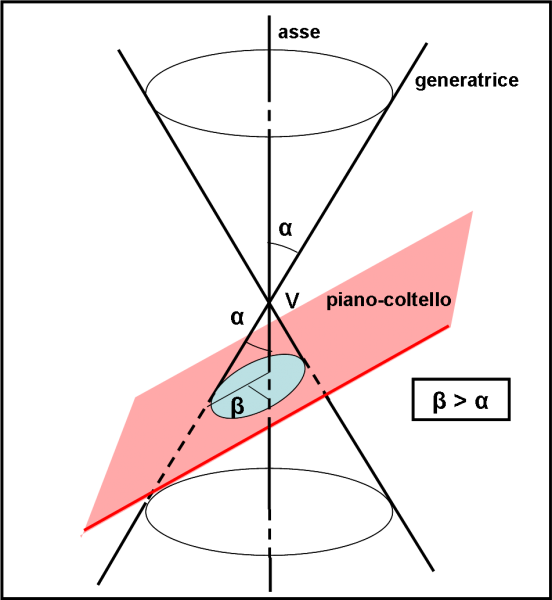
Va bene, va bene… ormai i punti fisici, geometrici o matematici non ci fanno più paura e andiamo avanti. Il passo successivo è quello di inclinare leggermente il piano-coltello rispetto all’asse a  come in Fig. 39. Chiamiamo β l’angolo tra piano-coltello e asse a. Nel caso dei tagli che portavano a circonferenze, questo angolo era, ovviamente, 90°. Diminuiamo l’angolo portando il piano-coltello verso l’asse. L’intersezione non è più una circonferenza, dato che si “allunga” sempre di più. Rimane, però, una curva chiusa come la circonferenza. Anzi, questa curva diventa la circonferenza solo nel caso particolare che β sia proprio 90°. La curva chiusa che si ottiene prende il nome di ellisse. La circonferenza è quindi una particolare ellisse, quella che si ottiene tagliando il cono con un angolo β = 90°.

La circonferenza, una figura tanto famosa e celebre, non è altro che un caso particolare di una curva (un po’ meno conosciuta) ben più generale. Se l’avessimo chiesto alla Fisica ce lo avrebbe detto subito. I pianeti e/o i satelliti rivolvono attorno alle proprio stelle e/o pianeti secondo orbite ellittiche, che possono avvicinarsi di molto alla circonferenza, ma che non lo saranno mai esattamente. Possiamo dire una frase, magari non troppo corretta, ma che ci fa intuire perfettamente il problema: la circonferenza è il limite a cui tende un’ellisse quando il piano-coltello tende a formare un angolo di 90° con l’asse a. Una soluzione matematica e non veramente fisica. Non assomiglia tanto al lungo discorso di Achille e la tartaruga?

Potremmo quindi concludere che in Natura è praticamente impossibile trovare una circonferenza. L’angolo β non sarà mai uguale a 90° ma tenderà a questo valore. In altre parole, esisterà sempre un angolo ε piccolo a piacere tale che 90 – β < ε. La circonferenza, come il punto, è un’entità matematica e non fisica. Ciò non toglie, però, che potremo tranquillamente studiarla e disegnarla come curva matematica, pur sapendo che non si potrà mai ottenere un risultato perfetto. Essa esiste solo come limite di un’ellisse. Scusate la ripetizione, ma ho voluto subito applicare i concetti discussi nelle lezioni precedenti a un caso solo apparentemente diverso.

Avrete sicuramente notato che finora ho usato solo una parte del cono (quella inferiore), mentre l’altra sembra fare solo da spettatrice. Avrei potuto disegnare solo delle semirette che partivano da V e non sarebbe cambiato niente. In realtà sì, ma non per molto…

Un altro “limite” del nostro coltello

Continuiamo a diminuire l’angolo β. L’ellisse si allunga ancora di più fino a un altro momento critico. Quale? Beh… è facile: quando l’angolo β diventa esattamente uguale ad α, come rappresentato nella Fig. 40.  Cosa implica questa situazione? Il piano-coltello taglia la superficie conica, ma la curva che ne risulta non si chiude più! Abbiamo trovato una curva aperta. Questo capita ovviamente perché le rette del cono vanno all’infinito e il piano-coltello, per quanto tenti di tagliare, non potrà mai tagliarle tutte. Il piano-coltello è parallelo a una generatrice e quindi non riuscirà mai a raggiungerla (se non all'infinito...)!

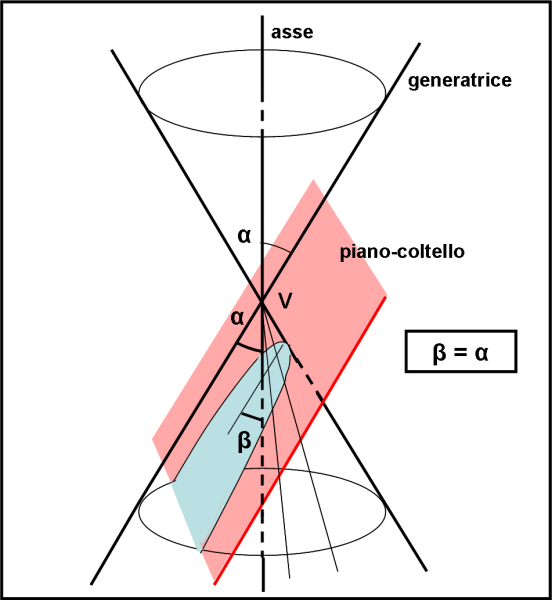
Siamo di fronte a una parabola. Una curva aperta, ma proprio per un’inezia. Bastava che l’angolo β fosse solo leggermente più grande di α (dato un ε piccolo a piacere, ecc., ecc.) e la curva sarebbe riuscita a chiudersi dando luogo a un ellisse, allungatissima, ma pur sempre un’ellisse. Le condizioni per ottenere una parabola sono estremamente critiche. Come vedremo tra poco, basterà che l’angolo β diventi appena appena più piccolo di α e la curva cambierà completamente forma e caratteristiche. Come la circonferenza, anche la parabola è una curva “limite”, ossia si ottiene solo e soltanto se l’angolo β è perfettamente uguale ad α. Una condizione matematicamente corretta, ma fisicamente impossibile. Possiamo perciò dire che anche la parabola è una curva limite, quella che si ottiene quando la differenza tra β e α tende a zero.

Ne parleremo in seguito, ma a qualcuno sarà già venuta in mente la cometa ISON o tante sue sorelle. Per convenienza, si considerano su orbite paraboliche, ma, come abbiamo visto, è una situazione fisicamente impossibile.

Come  le ellissi che si trovano facendo passare il piano-coltello per V, anche la parabola può “degenerare”. Basta che il piano coltello sia proprio tangente al cono o -se preferite- che contenga il punto V (è la stessa cosa, provate…). L’intersezione con il cono diventa solo e soltanto una retta, anzi proprio la retta generatrice “irraggiungibile” di prima. Se volete vedere la situazione sotto un altro aspetto, pensate di spostare il piano-coltello, parallelamente a se stesso, fino a passare per V. La curva si schiaccia sempre di più fino a coincidere con quella retta che risulta una specie di limite per la parabola che è essa stessa, in fondo, un limite. Un caso degenere interessa solo la matematica, un po’ come i punti singolari.

Notate, però, un fatto importante. Prima di raggiungere questa situazione limite del piano-coltello, le parabole che potevamo tracciare riguardavano sempre e comunque la parte inferiore del cono iniziale. Nel caso della parabola degenere, ciò che si ottiene è una retta, che continua, quindi, anche nella parte superiore del cono. Finalmente anche lei viene attivata!

Due curve invece di una

Andiamo avanti e incliniamo ancora di più il piano-coltello, ossia diminuiamo l’angolo β, che ormai è sicuramente più piccolo di α. Questa situazione porta a un risultato ormai del tutto previsto: il piano-coltello è obbligato a tagliare sia la parte bassa che quella alta del cono, come mostrato in Fig. 41. Non si ottiene più una sola curva, ma sempre due, simmetriche tra di loro. La curva così ottenuta prende il nome di iperbole, e le due parti da cui è composta si chiamano rami dell’iperbole.

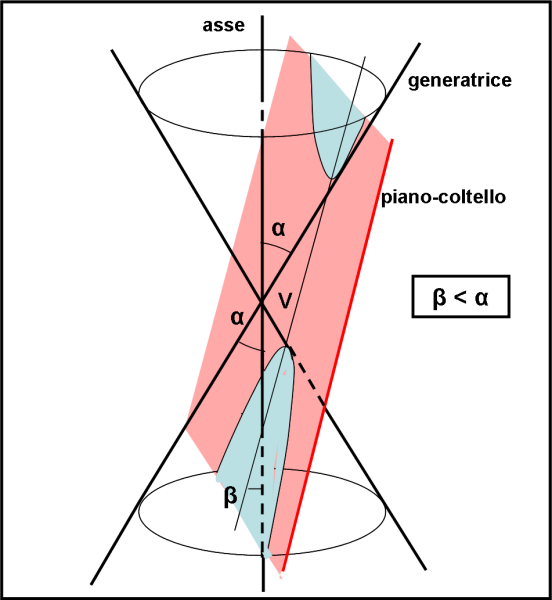
Cosa succede se facessi passare il piano-coltello per V? Ormai siamo esperti e non ci faremmo confondere. Avremo sicuramente una curva degenere. Infatti i due rami dell’iperbole si ridurrebbero a due rette (generatrici) che passano per il vertice V.

Continuiamo a diminuire l’angolo β fino a farlo tendere a 0. Otteniamo un’iperbole molto speciale, che è di nuovo un caso limite. Tuttavia, sarà quella più usata nella matematica elementare, dato che la sua equazione si semplifica di molto.

Anche l’iperbole è una curva (anzi due) aperta. Tuttavia, vedremo che se rappresentata nel piano cartesiano, i suoi rami tenderanno ad andare verso due rette molto speciali . Due rette che non raggiungeranno mai, ma tali che la differenza tra la curva e loro tenderà a essere sempre più piccola. E’ inutile che vi accenni al concetto di limite, ormai lo riconoscete subito! Se avete fretta di sapere, vi dico che sto parlando degli asintoti, ma su di loro torneremo in seguito e non solo per le iperboli.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica