Lo ammetto: questa parte è abbastanza lunga e pesante. Inoltre, necessita di grande attenzione e riflessione. Cercate di seguirla con calma senza farvi prendere dalla noia o dall’ansia di arrivare alla fine. L’iperbole è troppo importante in fisica per “snobbarla”. Se riuscite a seguire tutti i passaggi, siete già a buon punto per considerarvi matematici “abbastanza” esperti.

La curva si fa in due

Va bene, possiamo passare all’ultima conica, l’iperbole. Sicuramente è la curva meno “simpatica” e la meno “intuitiva” da costruire. Innanzitutto, ha un problema di fondo che già abbiamo conosciuto quando l’abbiamo identificata tagliando il nostro cono: è formata da due parti.

Definiamola come luogo di punti. Essa è composta dai punti che mantengono costante la differenza di distanza rispetto a due punti detti fuochi. C’è molto in comune con la definizione di ellisse, ma mentre là avevamo a che fare con la somma qui abbiamo a che fare con la differenza.

PF – PF’ = costante

Ciò implica proprio il fatto che  la curva si “apra”.  Vediamola in Fig. 48. L’abbiamo sistemata, come l’ellisse, con l’asse delle x che passa per i due fuochi e l’asse y che parte dal punto di mezzo tra di essi. Il risultato è, però, ben diverso.

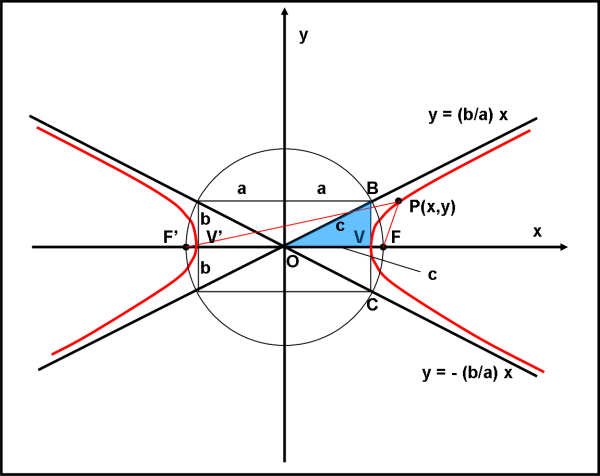
Quanto vale la costante? Agiamo come al solito e consideriamo un punto particolare dell’iperbole: il punto V, ad esempio, ma potevamo anche prendere V’. Anche per lui vale la relazione

VF – VF’ = costante

In questo caso però è chiaro che la differenza non è altro (data la completa simmetria) che la distanza tra i punti V e V’ (definiamoli pure vertici). Chiamiamo questa distanza 2a, dato che spesso useremo la sua metà, ossia la distanza a tra l’origine e i vertici. La distanza a prende il nome di semiasse (orizzontale), in modo simile all’ellisse. Possiamo quindi scrivere l’iperbole come:

PF – PF’ = 2a

La distanza tra origine e fuoco la chiamiamo c. Una distanza che, nuovamente, ci ricorda qualcosa dell’ellisse: la famosa eccentricità. Ricordate? Ebbene, anche in questo caso vale la stessa relazione:

e = c/a

Mentre nel caso dell’ellisse c (ossia la distanza del fuoco dall’origine) era sempre minore di a, e quindi e è era sempre minore di 1, adesso c è sempre maggiore di a e quindi e risulta sempre maggiore di 1.  Possiamo definire un parametro b, tale che:

b² = c² - a²    (c è maggiore di a)

b² = c² - a² = a²e² - a²  = a²(e² -1)

b = a(e² - 1)^1/2

Anch’esso possiamo chiamarlo semiasse, ma in questo caso b può anche essere più grande di a. Volete che ve lo dimostri? In fondo è utile per capire come quasi tutte le asserzioni possono essere verificate con una semplice formula e un po’ di ragionamento. Nel caso dell’ellisse avevamo:

b  = a(1 – e²)^1/2

e era sempre minore di 1. Cosa succedeva, allora, all’interno della radice quadrata. Toglievo sempre a uno una quantità minore di uno (il quadrato di qualcosa che è minore di uno è sempre minore di uno). Dentro la radice quadrata vi era quindi un numero minore di uno e tale rimaneva anche estraendone la radice quadrata. Ne conseguiva che per qualsiasi eccentricità (tra 0 e 1) a veniva moltiplicato per un numero minore di uno e quindi b era sempre minore di a. Nel caso della circonferenza, l’eccentricità era zero e quindi b diventava uguale ad a, ossia al raggio r.

Il caso della parabola non era trattabile, in quanto per e = 1 la radice quadrata andava a zero e quindi si annullava anche b. Non per niente la parabola è una curva “limite”.

Cosa succede, invece, adesso sotto la radice quadrata?

b = a(e² - 1)^1/2

Per valori di e poco più grandi di 1, anche il quadrato di e rimane poco maggiore di 1 e la differenza tra esso e uno è un numero minore di uno, così come la sua radice quadrata. b è effettivamente minore di a. Tuttavia, se e diventa molto più grande di uno, ad esempio 2, il suo quadrato diventa 4 e dentro la radice rimane 4 - 1 = 3, la cui radice quadrata è 1.73…, maggiore di uno e quindi b diventa più grande di a. Qual è il valore limite dell’eccentricità affinché b sia proprio uguale ad a? Non è difficile rispondere. Deve essere un numero il cui quadrato sia uguale a 2, in modo che dentro la radice rimanga uno e quindi anche la sua radice quadrata. a moltiplicato uno fa a e quindi b = a. L’eccentricità capace di fare questo gioco non può che essere la radice quadrata di 2, ossia 1,4142..., l’unico numero il cui quadrato è proprio 2.

Tutto questo discorso poteva essere evitato, dato che non è così fondamentale per la “nostra” matematica? Direi proprio di no. Innanzitutto, è stato un breve esercizio di logica matematica che porta a un risultato non così trascurabile. Inoltre l’iperbole che ha a = b e un’iperbole particolarmente “semplice” e utilizzata spesso dalla Natura… vedremo tra poco a cosa porterà.

Due curve limitate

Non posso certo nascondervi una particolarità di questa curva “doppia”. Essa si allarga come un parabola, ma è sempre contenuta all’interno di due rette. In altre parole, la y non riesce mai a superarle. Non che non vada verso il punto all’infinito, ma non può arrivarci prima delle rette che la confinano. Non preoccupatevi molto di quello che sto dicendo. Ci torneremo sopra diffusamente quando studieremo le funzioni (ora le stiamo solo definendo). Queste rette si chiamano asintoti e per come abbiamo disegnato il sistema di coordinate cartesiane, sono entrambe rette passanti per l’origine, ossia della forma y = mx. E’ difficile scriverle con quel che poco che sappiamo? Assolutamente no, ricordandoci la definizione di b. Riscriviamola:

b² = c² – a²   …. (12)

Una relazione del genere ci porta subito al solito teorema di Pitagora. In esso c deve essere l’ipotenusa e a e b i due cateti. Come facciamo a disegnarlo nella Fig. 48? Non è difficile. a sappiamo bene quello che è, la distanza tra O e V. c è invece la distanza OF. Disegniamo una circonferenza di raggio c e centro O. Costruiamo il triangolo rettangolo di vertici O, B e V, retto in V. La sua ipotenusa è proprio c (essendo un punto della circonferenza), il suo cateto AV è proprio a per definizione. Ne segue che VB deve essere, per il teorema di Pitagora:

VB² = OB² – OV² = c2 – a2

La (12) è confermata con VB = b

Le due rette verso cui tendono i rami dell’iperbole, senza mai raggiungerli, ossia gli asintoti, sono proprio le rette che passano per l’origine e per i vertici del rettangolo di lati 2a e 2b. Che equazioni hanno? E’ immediato rispondere sapendo che l’equazione di una retta che passa per l’origine è data da:

y  = mx

Nel nostro caso, sappiamo che una delle due rette deve passare per il punto B(a,b), quindi deve valere:

b = m a

Ossia:

m = b/a

L’altra, invece, deve passare per il punto C(a,-b). Segue quindi che ha un equazione:

y = m’x

e che

- b = m’a

Ossia:

m’ = - b/a

I due asintoti hanno quindi equazioni:

y = b/a x  

e

y = - b/a x

Come già detto, torneremo da loro quando studieremo le funzioni…

Possiamo, ancora, definire un’iperbole particolare: quella che ha a = b. In questo caso le due rette diventano y = x e y = -x, ossia proprio le rette inclinate di 45° rispetto agli assi cartesiani. L’iperbole prende in nome di equilatera. Sarà quella più utilizzata dato che i suoi asintoti sono, ovviamente, perpendicolari tra loro (45° + 45° = 90°).

Vedremo tra poco che essa avrà un’equazione molto più semplice e ci permetterà un giochino molto interessante con gli assi cartesiani.

Prima, però, è necessario effettuare il lavoro più pesante, quello dei monotoni e noiosi passaggi matematici. Potremmo anche trascurare il calcolo e prendere per buona l’equazione finale di un’iperbole come quella che abbiamo disegnato nella Fig. 48. Tuttavia, non è male ritornare su operazioni di spostamento e di semplificazione in cui appaiono dei prodotti notevoli. Per cui ho deciso di proporvela lo stesso, come fatto per l’ellisse e la parabola. Chi vuole può saltarla benissimo e prendere per buona l’equazione che segue:

x²/a² – y²/b² = 1  …. (13)

Come vedete non è molto differente da quella dell’ellisse, ma quel meno è decisamente importante per cambiare completamente la situazione. Non vi sembra? Anzi… qualcuno potrebbe svolgere da solo il calcolo e verificare se trova proprio l’equazione (13).

Ancora matematica

Il punto di partenza è sempre lo stesso. Dobbiamo scrivere in termini matematici l’espressione che definisce l’iperbole come il luogo dei punti la cui differenza da due punti detti fuochi rimane costante (e uguale a 2a). Le coordinate di P sono P(x,y), mentre quelle dei due fuochi sono F(c,0) e F’(-c,0). La relazione geometrica da tradurre in formula matematica è:

PF – PF’ = 2a

Avanti… partiamo!

PF = (y² + (x – c)²)^1/2

PF’ = (y² + (x + c)²)^1/2

(y² + (x – c)²)^1/2 - (y² + (x + c)²)^1/2 = 2a

(y² + (x – c)²)^1/2 = (y² + (x + c)²)^1/2 + 2a

y² + (x – c)² = y² + (x + c)² + 4a² + 4a(y² + (x + c)²)^1/2

y² + x² + c² - 2xc = y² + x² + c² + 2xc + 4a² + 4a(y² + (x + c)²)^1/2

- 4xc - 4a² = 4a(y² + (x + c)²)^1/2

- xc – a² = a(y² + (x + c)²)^1/2

x²c² + a⁴ + 2xca² = a²(y² + (x + c)²)

x²c² + a⁴ + 2xca² = a²y² + a²x² + a²c² + 2a²xc

x²c² + a⁴ = a²y² + a²x² + a²c²

x²c² – a²x² - a²y² = a²c² – a⁴

x² (c² – a²) – a²y² = a²(c² – a²)

x²b² – a²y² = a²b²

x²b²/a²b² – a²y²/ a²b² = a²b²/ a²b²

x²/a² – y²/ b² =  1

Come volevasi dimostrare.

Un’iperbole molto regolare

Nel caso in cui a = b (asintoti a 45° rispetto agli assi e, quindi, perpendicolari tra loro)

x²/a² –y²/a² = 1

x² – y² = a²   …. (14)

e gli asintoti saranno, come già detto y = x e y - x

Vi piace questa equazione, mostrata in Fig. 49? Sì, è semplice, ma si può rendere ancora più semplice. Cosa dobbiamo fare?

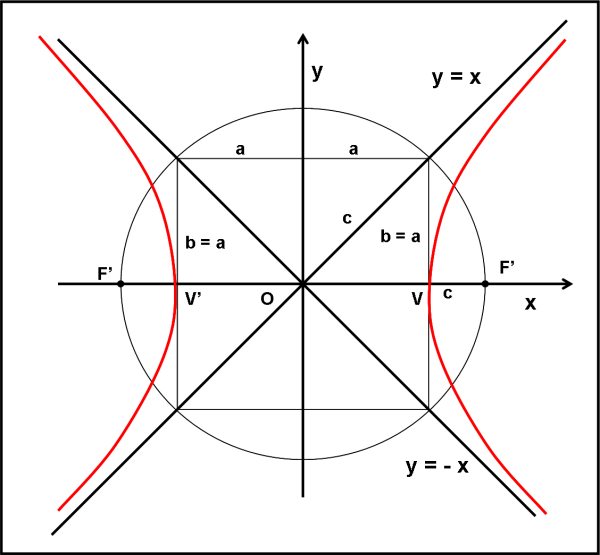
Trasformare gli assi cartesiani.

Cerchiamo di essere più chiari. Finora abbiamo fatto la scelta di prendere le ascisse e le ordinate seguendo la retta che passa per i fuochi e la sua perpendicolare in O. E se, invece, scegliessimo come assi cartesiani proprio gli asintoti?

Anche loro passano per l’origine e anche loro sono perpendicolari tra loro.  In altre parole dovremmo scrivere la nostra iperbole in funzione di coordinate definite sugli asintoti piuttosto che su coordinate definite sugli assi precedenti. In altre parole, dobbiamo scrivere il punto P di coordinate  x e y come fosse un punto P di coordinate X e Y, dove X e Y sono le coordinate misurate lungo gli asintoti.

Basterebbe trovare il legame che esiste tra x, y e X,Y e poi sostituire  nell’equazione (14) alla x e alla y la loro espressione in funzione di X e Y. La costruzione geometrica che ci permette questa trasformazione si ottiene facilmente guardando la Fig. 50, molto meglio che con tante  parole.

Ancora una volta, usiamo il teorema di Pitagora, ma, questa volta, su triangoli molto più semplici. Essi hanno un angolo di 45°. Ma se un angolo è di 45°, anche l’altro deve essere di 45°, dato che la loro somma deve essere 90°. Siamo di fronte a triangoli rettangoli isosceli, ossia con angoli uguali e quindi anche con cateti uguali. Cosa capita per triangoli di questo genere? Basta scrivere il teorema di Pitagora:

(ipotenusa)² = (cateto)² + (cateto)²

Ossia:

(ipotenusa)² = 2 (cateto)²

Estraiamo la radice quadrata da entrambi i lati:

ipotenusa = (2)^1/2 cateto

e quindi:

cateto = ipotenusa/(2)^1/2

Sintetizzando con poche parole: In un triangolo rettangolo isoscele i cateti (uguali tra loro) sono uguali all’ipotenusa divisa per la radice quadrata di 2.

Teniamo bene a mente questa conclusione, veramente elementare, e passiamo alla Fig. 50

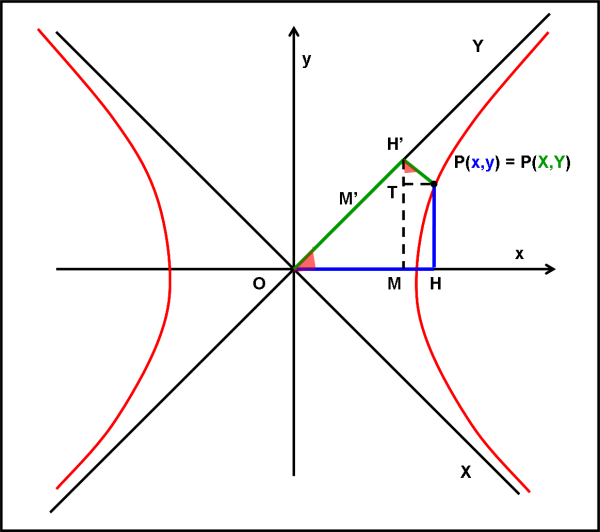
Consideriamo un punto qualsiasi della nostra iperbole equilatera. Esso ha coordinate x e y nel vecchio sistema di coordinate cartesiane. Lo stesso punto P, nel sistema cartesiano che ha per assi gli asintoti, ha invece coordinate X e Y. Ricordiamoci che gli asintoti formano angoli di 45° con i vecchi assi e  aspettiamoci che nascano facilmente triangoli rettangoli isosceli.

Le vecchie coordinate x e y sono disegnate in blu, quelle nuove X e Y sono disegnate in verde.

Quello che dobbiamo fare è cercare di esprimere le vecchie coordinate in funzione delle nuove, attraverso le relazioni geometriche che esistono tra asintoti e vecchi assi. Tracciamo qualche linea tratteggiata aggiuntiva che ci aiuti in questa piccola impresa. Da H’ (OH’ è la nuova ordinata Y) si traccia la perpendicolare all’asse x fino a toccarla in M. Da P tracciamo la perpendicolare a H’M, toccandola in T.  Abbiamo tutto ciò di cui abbiamo bisogno.

La vecchia coordinata x è uguale a OH. Possiamo, però, scrivere:

x = OH = OM + MH

Considerando il triangolo rettangolo isoscele OM H’, per quanto abbiamo detto poche righe fa:

OM = OH’/(2)^1/2

Dal triangolo rettangolo isoscele PTH’ si ha, analogamente:

TP = H’P/(2)^1/2       dove H’P è l’ascissa X del punto P nel nuovo sistema di coordinate

Ma TP = MH, quindi:

OH = OH’/(2)^1/2 + H’P/(2)^1/2

Sostituendo ai segmenti le coordinate nei due sistemi abbiamo:

x = Y/(2)^1/2 + X/(2)^1/2    …. (15)

Passiamo adesso a y:

La vecchia coordinata y non è altro che PH. Ma PH può essere anche scritto come:

y = PH = H’M – H’T

Quanto vale H’M? Usando il solito triangolo rettangolo isoscele OH’M:

H’M = OH’/(2)^1/2

Mentre, usando il triangolo rettangolo isoscele H’TP, si ha:

H’T = PH’/(2)^1/2

Ma OH’ =  Y  e   PH’ = X.           Segue che:

OH = Y/(2)^1/2 -  X/(2)^1/2            e quindi:

y = Y/(2)^1/2 - X/(2)^1/2    …. (16)

Non ci resta che sostituire la (15) e la (16) nella (14) e giocare un pochino con le solite regolette.

x² – y² = (Y/(2)^1/2 + X/(2)^1/2)² - (Y/(2)^1/2 - X/(2)^1/2)² = a²

Y²/2 + X²/2 + 2XY/2 – Y²/2 – X²/2 + 2XY/2 = a²

4XY/2 = a²

XY = a²/2

Ponendo k = a²/2 (k è una costante, dato che lo è a), si può scrivere:

Y = k/X     …. (17)

La Fig. 51 mostra come appare l’iperbole equilatera nel sistema di coordinate legate agli asintoti. Questi ultimi sono diventato gli assi cartesiani e hanno quindi equazione Y = 0 e X = 0.

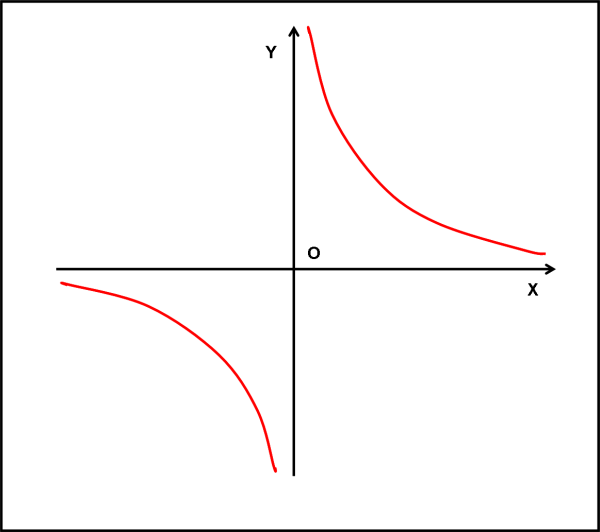
L’abbiamo già utilizzata in passato per mostrare i punti all’infinito della funzione y =1/x (ricordate?). Avevamo trovato che per x che tende a infinito la y tende a zero, mentre per x che tende a zero la y tende a infinito. Proprio ciò che capita quando due rette sono asintoti di una curva.

Largo alla fisica

La (17) è importantissima in fisica. Basta pensare alla definizione di densità. Essa vale:

d = M/V

Considerando la massa M una costante (la k di prima), abbiamo la relazione tra densità d e volume V. Questa relazione segue perfettamente il ramo destro di  un iperbole equilatera. Ma che dire dell’equazione di stato dei gas perfetti? Essa vale:

 pV = nRT

ossia :

p = nRT/V   

dove p è la pressione, T la temperatura e V il Volume. nR è una costante. Fissando la temperatura, la relazione ci permette di descrivere la pressione al variare del volume del gas e il viceversa.

Oppure, ricordiamo la formula che definisce il momento angolare in funzione della velocità angolare e del momento d’inerzia:

M = I ω

Nel caso di un momento angolare costante, si ha:

ω = M/I

che descrive come varia la velocità angolare al variare del momento d’inerzia che è poi legato alla massa e alla “forma” del corpo.

E cento altre leggi fondamentali della fisica…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica