Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Devo dire subito che gli eventi mutui, che saranno tra breve osservabili tra i satelliti di Giove, sono solo uno spunto per cercare di far capire come, secondo me, dovrebbero essere affrontati i fenomeni del Cosmo, da quelli più vicini a noi a quelli legati alle distanza inimmaginabili dell’Universo. Ormai mi conoscete bene e sapete che reputo fondamentale capire i concetti base, lasciando ai programmi prefabbricati il loro ruolo da “schiavi”, ossia di strumenti utili per sveltire i calcoli, ma sempre e comunque un mezzo e non un fine. Si usino pure, ma prima è necessario tornare al foglio e alla matita (e al cervello) per entrare veramente nella problematica, qualsiasi sia la difficoltà dei calcoli che si prospettano. Ricordiamo, inoltre, che un programma funziona solo se funziona la mente di chi lo ha progettato attraverso foglio e matita.

Giove e i suoi satelliti sono sempre stati una ghiotta occasione per gli astronomi. Essi sono ben visibili e mostrano, attraverso i loro movimenti reciprochi, una serie di fenomeni che possono migliorare costantemente (a mano a mano che la strumentazione utilizzata si raffina) molti parametri di importanza enorme per lo studio della dinamica e non solo. Ricordiamo che grazie a loro è avvenuta la rivoluzione scientifica galileiana e si è ottenuta la prima determinazione della velocità della luce per via astronomica. Insomma, un campo di battaglia mai obsoleto, a differenza di molti altri che ormai rimangono solo uno spettacolo prevalentemente mediatico. Chi ha l’attrezzatura fa bene a seguirli, tenendo però conto del vero interesse scientifico (non solo teatrale) e cercando di capire bene tutti i meccanismi che permettono la loro  esecuzione. Insomma, goderseli con lo spirito di questo blog.

Vi sono vari modi per introdurre i fenomeni mutui tra i satelliti di Giove. In realtà, l’articolo che avevo scritto su eclissi, occultazioni e transiti sarebbe già sufficiente per capire il succo del discorso. Tuttavia, vista l’importanza ancora attuale dei quattro oggetti medicei, vale la pena andare un po’ più a fondo. Quest’articolo, quindi, utilizzerà foglio e matita per  rendere semplici e intuitive le varie situazioni geometriche che sono alla base di tutto l’argomento, mostrando come siano un caso particolare di un quadro ben più ampio e generale. Arriveremo al bordo delle equazioni che portano alla loro risoluzione. Tuttavia, nessuna paura, non le affronteremo sia per la loro complessità sia per una certa monotonia che le accompagna. A questo serve il computer che , alla fine, fornisce dati ultra esatti che chiunque può trovare nel web. L’importante è capire come si impostano e cosa possono darci in cambio. Siamo sempre noi, però, che le prepariamo e nessun risultato grafico nasce da solo. Ciò che ci mostra un programma prefabbricato (da prendere a scatola chiusa) ce lo possiamo costruire da soli, con maggiore soddisfazione e ragionamento. Se, invece vogliamo dati veramente esatti, basta dare via libera alle equazioni e al “servo” che fa i calcoli. Insomma, vogliamo sia la carne che il pesce, ma non qualcosa che non sia né uno né l’altro.

Spero che queste mie esternazioni siano comprese per quello che vogliano significare. Uno stimolo per capire sia l’Universo e i suo giochi di prestigio, ma anche per saper dare una giusta collocazione al fantastico mezzo che è il calcolatore elettronico.

Divido l’articolo più parti (non so ancora quante, l’appetito viene mangiando…). Nella prima parte parto proprio da distante. Distante nel vero senso della parola. Immagino infatti di avere a disposizione un Kepler veramente sofisticato. Talmente sofisticato che è in grado di muoversi a piacere per sistemarsi nella posizione più vantaggiosa per osservare un sistema planetario attorno a una stella che non sia il Sole. Uso questo approccio perché è estremamente semplice e perché tutti hanno ormai capito perfettamente come funziona la strategia osservativa di Kepler (forse è meglio dire… come funzionava).

Quali sono i vantaggi di una partenza di questo tipo? Molti, sicuramente. Innanzitutto la sorgente di luce è una e una sola: la stella attorno a cui rivolvono i pianeti. Inoltre, la direzione secondo cui la Terra vede il sistema è una e una soltanto. Insomma, la situazione è quella che è e non “potremmo” teoricamente fare altro che accettare ciò che ci offre l’Universo con tutte le sue limitazioni. Se il piano orbitale dei pianeti ha un angolo particolare siamo in grado di vedere le eclissi, altrimenti si deve usare un’altra tecnica osservativa. A questo punto, entra in scena il Super Kepler, capace di muoversi secondo regole molto semplici e precise. Nessun sistema planetario potrà più avere segreti.

Vi sembra un discorso ben lontano da Giove e dai suoi satelliti? Assolutamente no. Piano piano il Super Kepler ci dimostrerà che la comprensione delle sue fantastiche (e semplicissime) capacità può accompagnarci facilmente verso le stagioni terrestri (e non solo) e, infine, con poche complicazioni, verso i fenomeni mutui che avvengono non solo nel sistema satellitario di Giove ma in qualsiasi altro, in tutte le configurazioni possibili. Userò, sempre e soltanto, foglio e matita e tutto scorrerà liscio come l’olio. Seguitemi e non ve ne pentirete.

Sicuramente, l’inizio vi sembrerà fin troppo banale e intuitivo. Benissimo. Solo partendo da cose semplici si può arrivare lentamente a quelle che sembrerebbero a prima vista molto complicate. Spesso, i programmi a scatola chiusa ce lo fanno pensare e… chissà che cosa sta dietro alla problematica. Assolutamente no, almeno per quanto riguarda i concetti di base per la comprensione completa del fenomeno. Tutt’altra cosa è il calcolo esatto di ciò che abbiamo capito ma di cui vogliamo avere risultati matematicamente perfetti. A questo punto, ben venga lo “schiavo” che svolgerà i calcoli e ci regalerà tutte le cifre decimali che vorremo.

La Fig. 1 ci mostra come funziona il Super Kepler. Cerchiamo di seguirla  attentamente, dato che è veramente banale. Il vecchio Kepler cosa farebbe? Bene, lui sarebbe in T1 (sulla Terra o molto vicino a lei, poco importa). In quella posizione osserva la stella S che ha due figlioli che le rivolvono attorno.  Beh… siamo abbastanza fortunati. L’equatore della stella è inclinato di un angolo φ non troppo grande rispetto alla direzione di T1. Ciò comporta una visione “frontale” come quella del riquadro relativo a T1. Uno dei due pianeti è abbastanza vicino alla stella per presentare delle eclissi mutue con la stella (chiamiamole eclissi o transiti o occultazioni, quello che preferite, il concetto è lo stesso: il pianeta passa davanti alla stella e dopo mezzo periodo è occultato da lei). L’altro, purtroppo, è troppo lontano e non riesce a fare lo stesso gioco. “Pazienza”, direbbe Kepler, “almeno uno l’ho beccato!”.  Notate che ho fatto un’ipotesi “fisica”, che posso tranquillamente accettare (soprattutto pensando ai sistemi satellitari che sono lo scopo finale del nostro racconto). Ho stabilito che i pianeti rivolvono sul piano equatoriale della stella secondo orbite circolari, ossia che  il piano orbitale di tutti i pianeti sia perpendicolare all’asse di rotazione dell’astro. Non è sempre vero, ma a noi basta e avanza. Studiando la situazione che osserva Kepler, è possibile stabilire, con queste ipotesi, l’angolo φ tra l’equatore della stella e la direzione di T1.

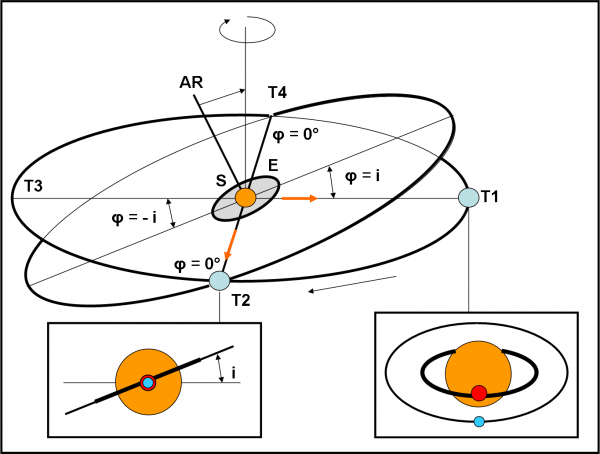
Possiamo accontentarci di questo risultato? Abbiamo avuto la fortuna di fare “trenta”, perché non fare “trentuno”. L’idea di base è: “Se esiste un pianeta, sarebbe bene cercare di trovare tutti i suoi fratelli. Magari non ci sono, ma per essere sicuri dobbiamo mettermi nelle condizioni ideali”. A questo punto entra in scena Super Kepler. Stabilito l’angolo φ, esso assume che questo non sia altro che l’angolo i tra il piano equatoriale del pianeta e un piano molto particolare che teoricamente esiste sempre (anche se non ha nessun significato fisico). Questo piano non è altro che il piano che contiene Super Kepler e la stella è e che è inclinato rispetto all’equatore dell’astro proprio dell’angolo φ. In altre parole posso determinare con facilità un piano inclinato dell’angolo i rispetto all’equatore della stella.

Ho solo cambiato nome all’angolo e costruito un piano teorico, niente di più. Tuttavia, mentre l’angolo i è un angolo fisso, tra due piani, l’angolo φ varia continuamente a seconda della direzione stella-Super Kepler. Sì, cari amici, questa è propria la caratteristica di Super Kepler. Esso è in grado di viaggiare nello Spazio, mantenendosi sempre alla stessa distanza dalla stella S. Dove avviene il suo movimento? Proprio nel piano che abbiamo appena costruito, inclinato dell’angolo i rispetto all’equatore della stella. Super Kepler descrive allora un’orbita (chiamiamola così) attorno alla stella, disposta su un piano perpendicolare alla retta verticale, che forma proprio, per costruzione, un angolo i con l’asse di rotazione della stella (perpendicolare all’equatore).

Non fatevi confondere da tante parole. Ciò che capita è comprensibile facilmente guardando la figura. Un foglio e una matita spiegano meglio di tante parole. Accendiamo i motori di Super Kepler e facciamolo girare attorno alla stella. Potremmo anche fermarci ogni tanto e vedere come cambia la configurazione geometrica stella-pianeti, ma sarebbe del tutto inutile, dato che il risultato è perfettamente prevedibile, per come è stato impostato il movimento di Super Kepler. Lo fermiamo, perciò, solo dopo 90° di rotazione. In quel punto il sistema planetario sarà in condizioni ideali. Non solo qualsiasi pianeta esistente passerà davanti (e dietro) alla stella, ma con un po’ di pazienza potremo anche vedere un pianeta passare davanti all’altro.

Perché capita questa fantastica situazione? Beh… ce la siamo costruiti noi. Siamo esattamente nel nodo tra il piano equatoriale del pianeta e il piano della pseudo-orbita di Super Kepler. In T2  l’angolo φ (angolo tra equatore e direzione ST2) diventa proprio zero e il piano equatoriale viene visto di “taglio”. Lo so, lo so, state già andando avanti col pensiero e state immaginando il moto della Terra intorno al Sole e il suo equatore inclinato di 23°. Anche lì abbiamo due piani inclinati tra di loro e la direzione Sole-Terra giace sul piano equatoriale della Terra nei suoi nodi con il piano dell’eclittica, ossia agli equinozi. Bravi, bravi…bene. Vi chiedo, però, di smettere di pensarci e tornare a Super Kepler. Arriveremo agli equinozi e alle stagioni un po’ più in là… Facciamo le cose con estrema calma… Abbiamo fatto volare una missione fantastica: vale la pena seguirla fino in fondo.

Osserviamo la stella in T2 e aspettiamo il momento in cui i due satelliti passano uno davanti all’altro (è bastata un po’ di pazienza). Magari non proprio come mostrato nel riquadro in basso, relativo alla vista frontale di T2 (troppa fortuna!), ma in qualche altra posizione lungo la loro orbita. Super Kepler ha scoperto tutto quello che c’era da scoprire e può rimettersi in moto.

Beh… non possiamo pretendere di più. Quando si arriva in T3, la situazione è identica a quella osservata in T1 (si invertono solo le eclissi tra stella e pianeta rosso), ma niente di nuovo. Quando arriviamo in T4 si ripete esattamente la configurazione ottenuta in T2. Non c’è da meravigliarsi, dato che siamo giunti nel secondo nodo delle orbite. Nessuna informazione supplementare, tranne che una constatazione: la visione migliore, quella che comporta sicuramente eclissi della stella da parte di tutti i pianeti e anche la loro reciproca occultazione, si ritrova esattamente dopo un tragitto di Super Kepler uguale alla metà del suo giro completo. In altre parole, se Super Kepler impiega un anno a girare attorno alla stella, le due configurazioni più interessanti avvengono a sei mesi di distanza una dall’altra (risultato più che ovvio, pensate ai nostri equinozi…). Se, invece, Super Kepler impiegasse 12 anni, le due condizioni ideali avverrebbero ogni 6 anni. Ricordatevelo, dato che 12 anni non è un numero scelto a caso…

Bene, la Fig. 1 non ha altro da dirci. Però, le capacità di Super Kepler vanno ben oltre. Passiamo a una caso estremamente particolare, ma molto interessante se pensiamo a Urano.

Immaginiamo che la situazione che vede Super Kepler in T1 sia quella della Fig. 2. Teoricamente, il nostro telescopio non vede assolutamente niente. Il piano equatoriale della stella è perpendicolare alla direzione T1-S e per vicini che siano i satelliti alla stella non possiamo aspettarci nessuna eclisse o transito o occultazione. Siamo nelle condizioni più sfavorevoli possibili. Tuttavia, noi non abbandoniamo la speranza e, non vedendo niente, facciamo l’ipotesi (che poi si rivelerà giusta) che la situazione sia proprio quelle della figura. Facciamo, perciò, partire Super Kepler lungo un orbita che giace su un piano perfettamente perpendicolare all’equatore della stella, supposto proprio perpendicolare alla direzione S-T1. Un gioco d’azzardo? Sì, ma non poi tanto… pensateci un po’ sopra e poi ne riparliamo.

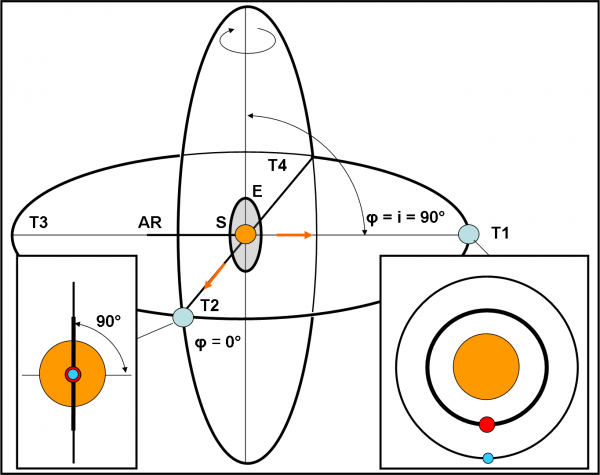
Super Kepler gira attorno al solito asse perpendicolare al piano costruito a tavolino. Che fortuna! Dopo 90° di rotazione le cose cambiano e come. La nostra ipotesi era giustissima. Il piano equatoriale della stella era proprio perpendicolare alla direzione S-T1. In T2, infatti, siamo nella linea dei nodi e si scoprono entrambi i pianeti che eclissano la stella e mostrano anche le loro reciproche occultazioni. Non c’è da dire molto di più, tranne che riflettere un attimo sul colpo di fortuna.

In realtà, il piano equatoriale poteva essere inclinato di un angolo piuttosto grande, ma non esattamente uguale a 90°. Tuttavia, anche facendo girare Super Kepler attorno a un asse non proprio “giusto”, avremmo trovato una posizione in cui il piano equatoriale sarebbe stato visto meno inclinato, permettendo di scoprire almeno un satellite e quindi anche il vero piano orbitale. A quel punto ci saremmo trovati di nuovo nelle condizioni della Fig. 1 e avremmo solo dovuto far cambiare orbita a Super Kepler. Insomma, solo un ritardo, ma la missione avrebbe comunque ottenuto lo scopo.

Torniamo alla Fig. 2. Il confronto con quella precedente ci dice che, per qualsiasi inclinazione dell’equatore della stella rispetto alla direzione stella-Super Kepler, è sempre possibile trovare una direzione in cui l’equatore si vede di taglio. Una soluzione ovvia, se ragioniamo in termini di piani inclinati di un angolo qualsiasi. Essi hanno sempre e comunque una linea dei nodi, ossia due punti in cui l’equatore viene visto di taglio.

Vi faccio notare un altro punto molto importante: finora abbiamo parlato solo di piano equatoriale della stella e direzione stella- Super Kepler o –se preferite- di una Terra che possa girare attorno alla stella. L’unico angolo importante è quello formato dall’equatore! Vedremo come sarà importante questo fatto quando arriveremo a Giove & Co.

Per completare una trattazione che è ormai diventata veramente banale e intuitiva, disegniamo anche la Fig. 3. Beh… qui siamo nel caso più fortunato possibile. Super Kepler non ha nessun bisogno di sprecare carburante. La stella ha il piano equatoriale proprio diretto verso di lui, ossia l’angolo tra equatore e direzione di vista è proprio zero. Senza nemmeno muoversi vediamo già il sistema planetario di taglio. Se costruissimo un’ipotetica orbita come quelle delle figure precedenti faremmo girare Super Kepler proprio nel piano equatoriale della stella. Qualsiasi direzione stella Super Kepler si comporterebbe come linea dei nodi. E’ ovvio: il piano orbitale e l’equatore coincidono!

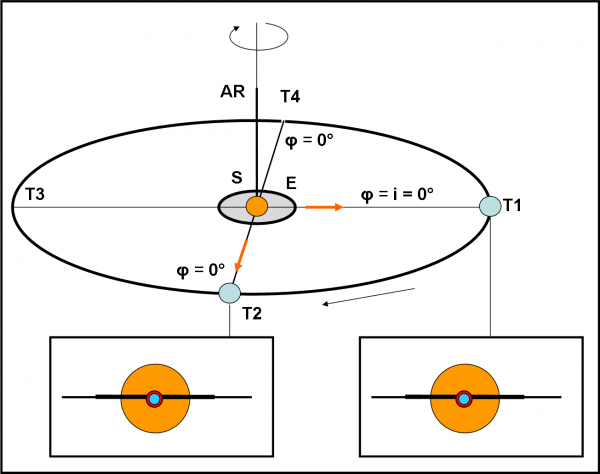
Prima di concludere questa prima parte, vi invito a riflettere su una constatazione molto importante (che interessa soprattutto lo studio delle curve di luce degli asteroidi: vedete quante applicazioni esistono se prendiamo un caso veramente generale?): per qualsiasi inclinazione tra due piani è sempre possibile trovare una direzione che mostri il piano equatoriale visto di taglio (la linea dei nodi). E’ invece unico il caso in cui si riesce a vedere il piano equatoriale “di fronte”, ossia perpendicolare alla direzione oggetto-osservatore. Ciò capita solo se l’asse di rotazione giace nel piano della pseudo-orbita. E questo fatto ci fa di nuovo pensare a Urano…

Possiamo chiudere qui. Vi invito a leggere e rileggere questa prima parte: se capite bene questa trattazione semplificata, non vi saranno più problemi per comprendere la più complessa geometria del sistema di Giove (o di Saturno o del pianeta che volete). Basterà cambiare la pseudo orbita di Super Kepler con un movimento che la Terra compie realmente. Impareremo, tra l’altro, che l’inclinazione dell’orbita di Giove riveste un’importanza del tutto trascurabile, contrariamente a quanto, a volte, si legge sul web.

Alla prossima e, sempre, con foglio e matita!