Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Prima di continuare nel nostro lento avvicinamento a Giove e ai suoi figlioli, fatemi ricapitolare quanto abbiamo appena imparato da Super Kepler.

1)      Indipendentemente dall’inclinazione esistente tra piano equatoriale del sistema stellare e linea di vista, se potessimo girare intorno a lei come fa Super Kepler, troveremmo almeno una configurazione che ci permette di assistere al transito dei pianeti davanti alla stella.

2)      Questa configurazione è però fin troppo fortunata, in quanto non solo permette di assistere al transito dei pianeti davanti alla stella, ma ci fa vedere il piano equatoriale proprio di taglio.

Imparate queste nozioni banalissime, lasciamo per un attimo da parte il nostro Super Kepler (SK) e torniamo al più concreto Kepler o, addirittura, alla Terra.

In altre parole, accontentiamoci, per adesso, del passaggio dei pianeti davanti alla stella nelle condizioni che la fortuna ci ha regalato, ossia la posizione relativa dell’ equatore della stella rispetto alla linea di vista. Come ben sappiamo, le condizioni di visibilità di un sistema planetario dipendono dall’ inclinazione sotto la quale vediamo l’equatore della stella, sempre sotto l’ipotesi che i pianeti rivolvano in quel piano.

Sì, giustissimo, ma ciò che veramente comanda tutto il gioco sono il diametro della stella e la sua distanza dai pianeti. Indipendentemente da dove si trovi l’osservatore (Kepler), cosa determina chi e come vede i transiti o eclissi, o quello che volete, dipende primariamente dalla geometria intrinseca del sistema stellare.

Avviciniamoci quindi alla stella e scopriamo le condizioni di osservabilità che essa e i suoi pianeti impongono a chiunque voglia assistere alla loro danza. Una semplicissima analisi grafica ci permette di scrivere le condizioni limite. Un gioco veramente da ragazzi che probabilmente avevo già trattato in articoli precedenti, ma che vale la pena riproporre per non obbligarvi a saltare di qua e di là. Disegniamo, allora, la Fig. 4. Niente si speciale… Al centro la stella A che ha un certo raggio r. Orizzontalmente ho tracciato il suo equatore (immaginiamo di vedere il tutto in un piano perpendicolare all’equatore, quello che ci permette di ottenere i parametri più importanti, come vedremo tra poco).

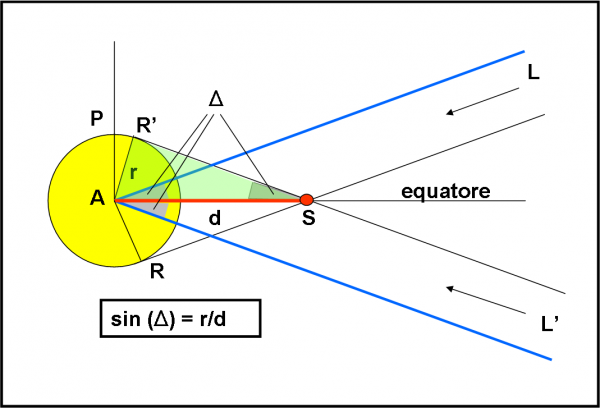
Basta conoscere il raggio della stella? Assolutamente no. E’ anche necessario sapere la distanza dei pianeti dalla stella. Per poter assistere ai transiti di ogni figliolo, consideriamo ovviamente quello più esterno (più lontano dalla stella), dato che è sicuramente lui quello che limita di più le condizioni di visibilità.  Chiamiamo questa distanza d. Abbiamo, adesso, tutti i parametri per scoprire chi e come può vedere i transiti planetari. Ci interessa ovviamente la soluzione limite, ossia quella che permette di vedere l’ultimo satellite sfiorare il bordo della stella. Un leggero spostamento (vedremo da che parte) annulla i nostri sforzi.

Non è difficile tracciare la direzione dell’osservatore L’ che vede questa condizione limite. Basta disegnare la linea che passa per il pianeta S ed è tangente alla stella, ossia R’S. Chi si trova lungo questa direzione assiste proprio a un contatto istantaneo del pianeta S con la stella A. Basterebbe inclinare un po’ di più questa direzione verso il basso e il pianeta S non toccherebbe più la stella e addio transito! Qual è allora l’angolo limite per il sistema stellare che vogliamo osservare? Facilissimo a dirsi e a disegnare: l’angolo Δ tra la direzione L’R’ e l’equatore della stella (dove risiedono per definizione tutti i suoi pianeti). Ovviamente, si ha una situazione del tutto analoga ribaltando la situazione nella parte alta. In questo caso la direzione è  individuata da RS ed è indicata da L. Da L vediamo il pianeta toccare la stella nel suo estremo inferiore; da L’ vediamo una configurazione identica, ma nella parte alta. Per noi, comunque, è la stessa cosa: non facciamo differenze tra alto e basso (che non esiste nell’Universo). L’angolo RAS  è, quindi, uguale a R’AS.

Per comodità di disegno, tracciamo le due linee azzurre che partono dal centro della stella A. L’angolo che esse formano rispetto all’equatore è, ovviamente, identico a Δ. Non fatemelo dimostrare… abbiamo di fronte angoli alterni interni tra rette parallele (L’R’ e L’A), tagliate da una trasversale (AS). Come ben sappiamo, essi devono essere uguali. So che è del tutto inutile, ma fatemi aggiungere un piccolo commento. Ho definito due rette parallele con un punto in comune (L’). Com’è possibile? Beh… ormai siete esperti! Quel punto L’ è un punto che può essere considerato all’infinito, dato che la distanza dell’osservatore è enormemente più grande della distanza pianeta-stella e del raggio della medesima. Possiamo, quindi, tranquillamente considerare parallele le linee che provengono da un osservatore lontanissimo. Avete visto come vengono utili le “lezioni” sul punto all’infinito del nostro piccolo corso di matematica?

Torniamo a noi e consideriamo il triangolo rettangolo verde AR’S (ma potevamo anche prendere ARS).  Di questo triangolo, che è rettangolo dato che R’ è il punto di contatto della tangente al cerchio e quindi forma un angolo retto con la direzione R’A, conosciamo un cateto (r) e l’ipotenusa (d). Che cosa vogliamo ricavare? Beh… semplicissimo: l’angolo limite di visibilità, ossia Δ.  Non ci spaventiamo di certo, dopo aver già introdotto le funzioni trigonometriche più semplici. Ricordate la definizione di seno di un angolo? Beh… ve lo ripeto: il seno dell’angolo Δ è dato dal rapporto tra ipotenusa e cateto opposto all’angolo. Possiamo quindi scrivere:

sin (Δ) = r/d

Conosciamo r e d e quindi è immediato calcolare l’angolo Δ. Conoscendo il seno, si sa anche qual è l’angolo il cui seno è il rapporto r/d. Al limite, potete usare un’obsoleta calcolatrice tascabile… ve lo concedo.

Guardiamo ancora, per un attimo, la Fig. 4, dove, come già detto, abbiamo tracciato le due rette azzurre che individuano le due direzioni limite da cui si riesce ancora a vedere (anche se al pelo) un transito del satellite più esterno. L’angolo tra equatore e le due rette è, per costruzione, proprio Δ. Cosa possiamo concludere con un semplicissimo ragionamento? Beh… se l’osservatore è meno inclinato, rispetto all’equatore, dell’angolo Δ non ha problemi a vedere i transiti. Se invece è inclinato di un angolo maggiore di Δ, non riesce assolutamente a vedere il transito del pianeta S.

Ovviamente, se abbiamo a disposizione Super Kepler, anche quest’ultima configurazione non ci spaventa: basta farlo girare e prima o poi arriverà nei famosi punti trovati la volta scorsa, ossia nei nodi della sua pseudo-orbita con l’equatore della stella. Ma basta anche molto meno. Avevo promesso, però, di non usarlo più (almeno per adesso) e quindi torniamo alla Fig. 4 e alle sue conclusioni.

Qualcuno potrebbe dirmi: “Ti piace vincere facile! E’ ovvio che hai risolto il problema. Sei partito sapendo sia il raggio della stella che la distanza dei pianeti. Ma Kepler queste cose non le sa assolutamente!”. Ovviamente, avrebbe ragione… ma a noi, per lo scopo dell’articolo, interessa fare il procedimento inverso rispetto a quello che esegue Kepler. Lui osserva i transiti (quando li osserva) e in base a ciò che vede riesce più o meno a calcolare la geometria del sistema stellare. Noi, invece, sappiamo in anticipo la geometria del sistema stellare e vogliamo scoprire dove si deve trovare l’osservatore per assistervi. Ricordiamoci, infatti, che siamo partiti dalle stelle, ma vogliamo arrivare a Giove (e magari anche agli altri pianeti) e ai suoi satelliti. In questo caso conosciamo perfettamente le configurazioni orbitali!

Prima di trasferirci nel Sistema Solare, cerchiamo di fare gli astronomi seri. Un passo in più (forse non del tutto necessario) che permette, però, una descrizione più gestibile e più vicina a quella che viene eseguita dai professionisti e poi data in pasto ai servi “calcolatori”. Noi vogliamo giungere a quel punto e non certo limitarci a quello che ci viene propinato dai programmini  a "scatola chiusa” che vogliono solo stupirci con effetti speciali, ma che non spiegano assolutamente niente. Proprio come i media, che ci assillano da tutte le parti, queste “pappe pronte” creano spesso molta confusione e molto siti web se ne cibano a occhi chiusi, senza capirne i concetti, commettendo così errori anche gravi (primo fra tutti proprio Wikipedia).

Cosa vogliamo fare esattamente. Non spaventatevi… una cosa che facciamo costantemente quando guardiamo il cielo. Considerare ciò che si vede come se fosse proiettato su una sfera, la sfera celeste. Ogni stella, pianeta, galassia, asteroide, satellite, ha una posizione ben precisa su di essa. Se usassimo un nome proprio o un “nickname” per ogni oggetto celeste sarebbe un bel caos. Molto meglio dare un nome e un cognome a ogni corpo celeste che si vede (con tutti gli occhiali possibili). Dalla geometria si sa benissimo che ogni punto di una sfera può essere individuato da un paio di coordinate, in un certo sistema di riferimento.

Lavorando su una sfera (e non su un piano) queste coordinate non sono segmenti rettilinei come la x e la y del piano cartesiano (che ormai conosciamo molto bene), ma degli archi di cerchio. Abbastanza semplice, in principio. Bisogna però definire il sistema di riferimento. Per le coordinate cartesiane si usava un punto origine e due assi perpendicolari tra loro. Per la sfera celeste si usano cerchi e punti di partenza particolari da cui misurare gli archi di cerchio. Non voglio farla troppo lunga e nemmeno introdurre tutti i sistemi di riferimento che si usano in astronomia (magari lo faremo in un articolo a se stante). Consideriamone quindi uno particolarmente favorevole per gli scopi dell’articolo. Dove stanno i pianeti (o i satelliti) di una stella (o di un pianeta)? Beh, lo sappiamo ormai bene: nel piano equatoriale dell’oggetto di riferimento. Consideriamo allora proprio l’equatore come cerchio fondamentale sulla sfera celeste. Una soluzione comunissima per descrivere il nostro pianeta e che porta alla definizione dei meridiani e dei paralleli. La conosciamo sicuramente molto bene. Usiamo, allora, la stessa strategia per rappresentare i risultati che abbiamo conseguito finora.

Più di tante parole vale la Fig. 5. Al centro mettiamo la stella A. Il piano di riferimento è il suo equatore (il cerchio rosso) che è stato disegnato orizzontalmente (ma potevo disegnarlo come volevo). Definito il piano equatoriale è immediatamente definito anche il polo P. Dato un punto qualsiasi Q sulla sfera celeste, esso può essere univocamente identificato attraverso due coordinate “sferiche”. La prima si ottiene tagliando la sfera con un piano passante per il polo e per l’ oggetto Q, perpendicolare all’equatore. I cerchi che si ottengono dall’intersezione di questo piano con la sfera vengono chiamati meridiani. La prima coordinata, chiamata declinazione e indicata con δ, è l’arco di circonferenza misurato sul meridiano corrispondente, che va dall’equatore al punto Q. La seconda coordinata si misura invece lungo l’equatore a partire da un punto che si può scegliere un po’ come si vuole. Per la Terra si usa spesso il punto di Ariete, quello relativo all’equinozio di primavera. Esso indica il passaggio del Sole da declinazioni negative a declinazioni positive. Per la nostra stella, potremmo scegliere uno dei nodi con la traiettoria apparente di Super Kepler.

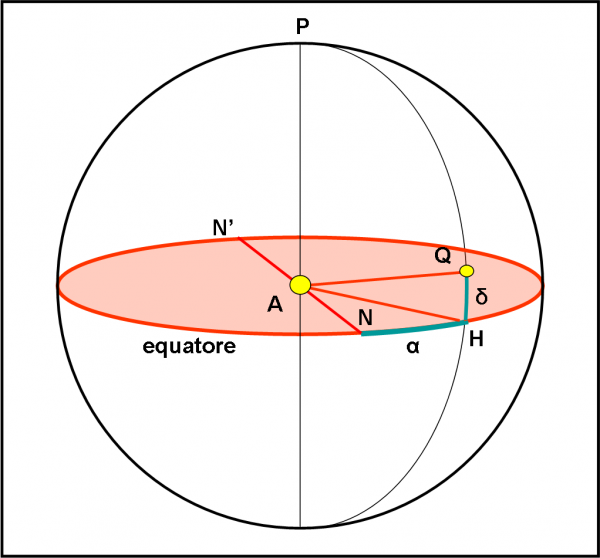
Tra breve lo faremo, ma, per adesso, non diamogli troppa importanza e consideriamo un punto N più o meno qualsiasi. L’arco di cerchio misurato lungo l’equatore da questo punto al meridiano di prima viene chiamata ascensione retta e indicata con α. Tuttavia, per adesso, poniamo l’attenzione solo sulla declinazione.

Prima di proseguire, sento di dover chiedere scusa a molti lettori  (magari a tutti). Aver descritto le coordinate equatoriali è forse stato un passaggio davvero inutile. Tuttavia, per non cadere in qualche trabocchetto nella sua applicazione più generale, ho pensato che non era male avere sottomano una definizione saputa e risaputa, ma magari mai analizzata con la dovuta attenzione. Insomma, al limite, cancellate la parte precedente…

Torniamo alla sfera celeste della stella A e alle sue coordinate equatoriali. E’ molto semplice disegnare la Fig. 6 che altri non è che la Fig. 4, “compattata” e visualizzata in tre dimensioni.  Analizziamola con la dovuta calma, dato che ci permetterà di arrivare fino a Giove e a tutti i pianeti che vorremo.

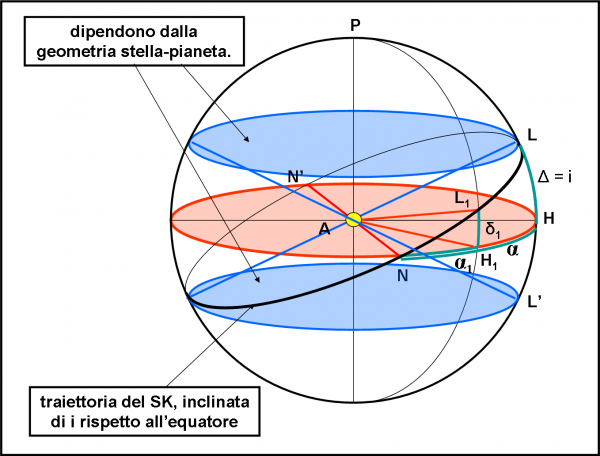
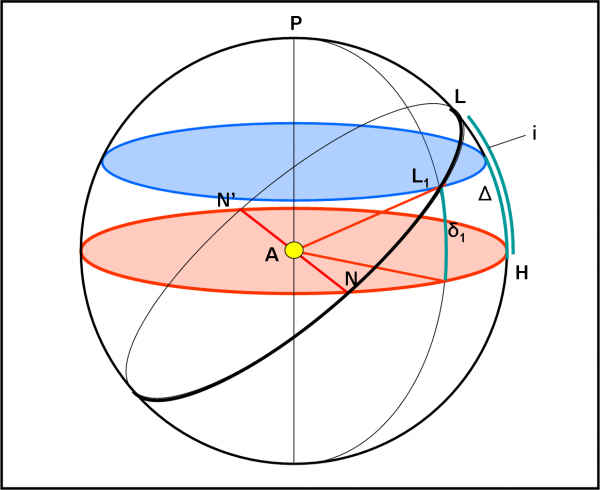
Tracciamo le due rette AL e AL’ nel piano del foglio. Esse individuano subito due “paralleli” azzurri, luogo dei punti che riescono a vedere i transiti nelle condizioni limite. Tutti questi punti hanno declinazione Δ. Limitiamoci, per semplicità, ad analizzare le direzioni L e L’, intuendo che la stessa cosa capita per ogni meridiano e per le sue intersezioni con i paralleli azzurri. E’ giunta l’ora di rimettere in moto Super Kepler e facciamolo partire dal punto L. Esso descrive un cerchio massimo, ossia un cerchio che ha centro nell’origine A. L’inclinazione i di questo cerchio nero rispetto all’equatore è esattamente uguale (per costruzione) all’angolo limite Δ. Essendo partiti da una posizione che, benché al limite, permetteva di vedere il transito più esterno “al pelo”, Super Kepler non fa che migliorare la sua osservazione (i transiti avvengono sempre più centrali). Ottiene il meglio del meglio quando arriva in N (e N’), ossia nei nodi della sua orbita rispetto all’equatore stellare. Queste considerazioni seguono perfettamente quanto descritto nell’articolo precedente. Una posizione L₁ intermedia lungo l’orbita di Super Kepler ha una certa declinazione δ₁. Avendo definito anche i nodi di quest’orbita (o pseudo-orbita come preferite), possiamo far partire l’ascensione retta α da N. L₁ ha, quindi, α₁ = NH₁ e L ha α = NH. Tanto per completezza… anche se per adesso ci interessano poco.

Direi che tutto è piuttosto chiaro. Ricapitolando: abbiamo inserito le condizioni di visibilità del transito del pianeta di un sistema stellare in un sistema di coordinate, adatto a qualsiasi trasformazione o calcolo che utilizzi la trigonometria sferica (nel caso volessimo cambiare sistema di riferimento). Ricordiamo inoltre un fatto fondamentale che non dobbiamo assolutamente dimenticare: il parallelo azzurro dipende solo e soltanto dalla geometria del sistema stellare (raggio dell’astro e distanza del pianeta più esterno) e non da altri parametri. Il cerchio massimo nero indica invece la traiettoria di SK, ossia la traiettoria di un oggetto celeste (anche se artificiale), che descrive un’orbita circolare attorno alla stella con un’inclinazione i data proprio da Δ. Questa traiettoria è molto particolare, dato che è quella che corrisponde a un caso limite, ossia a quello che vede i transiti planetari in ogni suo punto e che arriva al limite estremo (in L). Un’orbita di confine in altre parole.

Attenzione: i è un angolo fisso tra due cerchi massimi (equatore e traiettoria di SK), mentre δ è la coordinata del sistema di riferimento, variabile da punto a punto. In condizioni limite (L) la declinazione massima di visibilità Δ coincide proprio con l’inclinazione orbitale i. Ovviamente, la stessa cosa, ribaltata, capita nell’emisfero sud. Scusate la ripetizione, ma questo concetto è fondamentale per  il prosieguo dell’articolo. Ne vediamo subito una conseguenza nella Fig. 7, dove, per fare meno confusione, abbiamo eliminato la parte bassa, del tutto simile a quella alta.

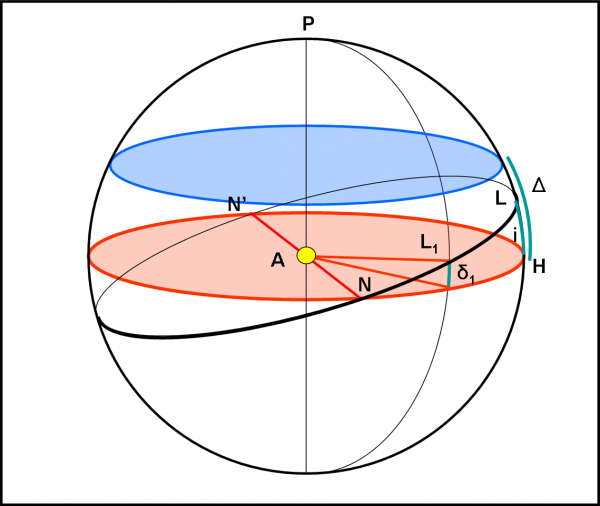
Il parallelo azzurro è rimasto tale e quale, dato che il sistema stellare è sempre lo stesso. Abbiamo cambiato, però, l’osservatore L. L’inclinazione della retta LA rispetto all’equatore è minore dell’angolo limite Δ. Questa inclinazione i è proprio quella dell’orbita di SK. Un’orbita che parte già da una posizione fortunata (benché sia la “peggiore” possibile), dato che L vede tranquillamente i transiti, essendo i (ossia la declinazione di L) minore dell’angolo limite Δ. A maggior ragione, tutti i suoi punti vedranno tranquillamente i transiti fino a ottenere il caso perfetto (equatore visto di taglio) in N. I nodi non sono cambiati rispetto a prima, dato che il nuovo L si trova sullo stesso meridiano del caso precedente.

Adesso, ridisegniamo in Fig. 8 la figura di prima (identico sistema e identico parallelo azzurro), ma per una direzione dell’osservatore L che formi una angolo i maggiore dell’angolo limite Δ (che dipende solo dal sistema stellare, ricordiamolo!). Ormai sappiamo bene come fare. La traiettoria di SK parte da un punto sfortunato (non vede i transiti), dato che i è maggiore di Δ, ma inizia a osservare il primo punto di contatto quando giunge in L₁. Non ci dobbiamo certo stupire che L₁ abbia declinazione δ₁ proprio uguale a Δ. Il parallelo azzurro, proprio perché è un parallelo, deve mantenere la stessa declinazione, essendo “parallelo” all’equatore.

Cari ragazzi, sto dicendo cose che potrebbero sembrare delle novità. Assolutamente no. Non faccio altro che descrivere meridiani e paralleli… Pensateci bene. Sto applicando ovvietà, conosciute da tutti, a una situazione particolare. Tutto qui… e senza nessun bisogno di Celestia o “pappe pronte” del genere… Eppure, abbiamo già in mano tutti i parametri che ci permetteranno di applicare la situazione al sistema di Giove e non solo. In particolare, le coordinate che abbiamo utilizzato ci forniscono i dati esatti affinché un computer ottenga risultati del tutto professionali.

Non pensate che ce l’abbia con certe rappresentazioni pseudo-tecnologiche per partito preso. Sono convinto che siano utilissime, ma solo dopo aver compreso come funzionano le cose. Purtroppo, spesso e volentieri, si utilizzano “invece di” e non “dopo”. Le conseguenze sono molte volte una grande confusione, varie inesattezze e l’idea che certe cose siano possibili solo agli addetti ai lavori. Continuerò a lottare per dimostrare che con un po’ di fatica mentale (sicuramente anche divertimento per la maggior parte di voi) la realtà è molto più semplice di quanto si pensi.

Torniamo a noi… Cosa dobbiamo fare per passare al nostro Sistema Solare? Cambiare il ruolo della stella e di SK. La stella e i suoi pianeti diventano Giove e i suoi satelliti, mentre SK non è altro che, nel primo caso che tratteremo, un oggetto celeste “naturale” molto ben conosciuto: il Sole!

Vi lascio soli… a riflettere e a provare di fare autonomamente il passo successivo, in attesa del prossimo articolo.

E sempre con foglio e matita  (e ragionamento), mi raccomando!