Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Qui, sulla Terra, siamo abbastanza contenti, ma ci dispiace un poco non aver visto direttamente i transiti. Come potremmo fare? Beh… si potrebbe usare la stessa Terra come Super-Kepler costringendola a girare attorno a Giove e ai suoi figlioli. Purtroppo, malgrado la tecnologia sia ormai eccezionale, spostare la Terra a piacimento rimane ancora un problema insolubile. Dobbiamo rassegnarci? Beh… non è detto. Anche il nostro pianeta potrebbe fare concorrenza al Sole. E’, in effetti, anche lui un Super-Kepler, anche se  un po’ indipendente e bizzarro.  Si comporta come se fossimo tornati ai tempi di Tolomeo, quando gli epicicli riuscivano a spiegare i moti dei corpi planetari. Accidenti, le cose si complicano e, forse, dovremmo iniziare ad affidarci ai programmi “a scatola chiusa”… Macché, state tranquilli: basta ancora il foglio e la matita, con l’aggiunta di un pizzico di attenzione e di voglia di capire.

Un Super Kepler irrequieto

Vediamo qual è la situazione relativa al magnifico terzetto Sole, Giove, Terra. Finora abbiamo sempre immaginato che sia il Sole a rivolvere attorno a Giove. Abbiamo sbagliato? Assolutamente no. Lo facciamo continuamente per la coppia Terra-Sole e quindi possiamo continuare a farlo, invertendo le posizioni. Il problema, come abbiamo visto prima, è che lo stesso stratagemma non possiamo farlo direttamente tra la Terra e Giove. Tuttavia, se il Sole gira attorno Giove e se la Terra gira attorno al Sole, possiamo dire che, in modo un po’ strano, anche la Terra DEVE girare attorno a Giove.

Il nostro pianeta si fa trascinare dalla stella nel suo moto “apparente”. Non è forse quello che fa la Luna? Anche lei gira intorno alla Terra, mentre la Terra gira intorno al Sole. E’ una situazione che conosciamo molto bene. In fondo, in fondo, anche la Terra può essere considerata un Super-Kepler dato che segue il Sole, pur danzandogli attorno. Molto meglio rappresentare queste banali considerazioni in Fig. 25.

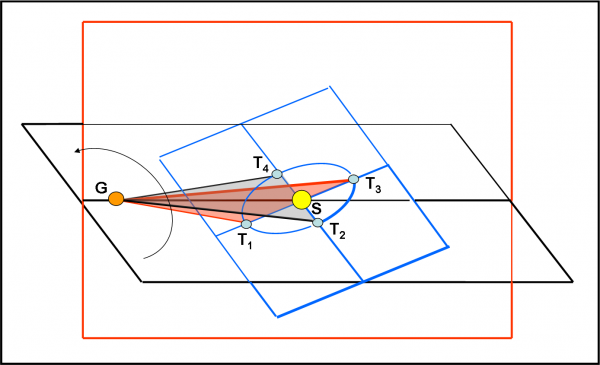
Ho disegnato i tre piani fondamentali. Quello nero (orizzontale) è il piano dell’orbita di Giove attorno al Sole, ossia del Sole attorno a Giove. Quello azzurro è il piano orbitale della Terra (eclittica), inclinato di un certo angolo rispetto a quello precedente (che è poi l’inclinazione del piano orbitale gioviano rispetto all’eclittica). Infine, quello rosso è perpendicolare al piano di Giove.

Blocchiamo con una bacchetta magica la situazione ad un certo istante della rivoluzione del Sole attorno a Giove. Lasciamo muovere solo la Terra e evidenziamo quattro punti particolari lungo la sua orbita: T₂ e T₄ non sono altro che i nodi tra l’eclittica e il piano dell’orbita gioviana; T₁ e T₃ sono invece i punti in cui si raggiunge la massima distanza angolare tra la Terra e il Sole, vista da Giove. Uno sarà “sopra” il piano di Giove e l’altro “sotto”. I due angoli non sono uguali, dato che in una caso la Terra si trova più lontana da Giove e nell’altro più vicina di quanto non sia ai due nodi. Questi due angoli sono sempre più piccoli dell’inclinazione del piano di Giove rispetto all’eclittica, dato che la distanza Terra-Sole è decisamente più piccola di quella tra Giove e il Sole.

Conoscendo le distanze dei due pianeti dal Sole e della Terra da Giove, esiste una formula trigonometrica che permette di ricavare l’angolo che ci interessa. Magari ne parleremo, ma per adesso sappiamo che si può calcolare facilmente.

Nella figura ho solo indicata con una freccia l’orbita del Sole attorno a Giove,  per non allargare  troppo il disegno.

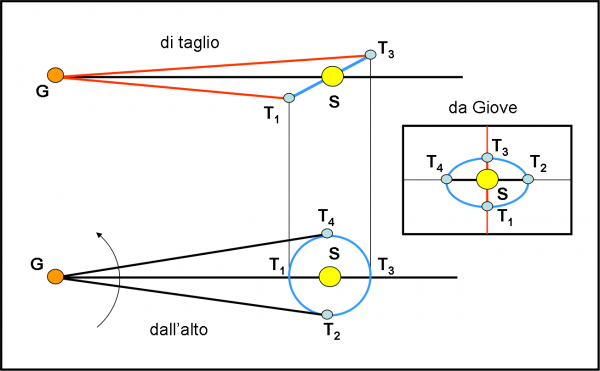
Nella Fig. 26 vediamo, adesso, la figura di prima proiettata nei due piani, quello rosso e quello nero, ossia quello perpendicolare all’orbita di Giove (sopra) e quello che contiene l’orbita di Giove (sotto). Possiamo anche dire che il primo fa vedere l’orbita della Terra (azzurra) di taglio e il secondo dall’alto (o dal basso, tanto è uguale…). Ancora più interessante è vedere la coppia Terra-Sole da Giove su un piano perpendicolare alla direzione Giove-Sole, come mostrato nel riquadro a destra. Beh… dovevamo aspettarcelo: la Terra descrive una specie di ellisse attorno al Sole che ha la distanza verticale superiore minore di quella inferiore (i famosi angoli differenti di cui abbiamo parlato prima), ma che si allontana verso destra e verso sinistra dello stesso valore (siamo ai nodi, ovviamente).  Questa danza attorno al Sole dura, ovviamente, un anno. L’importante è, però, che due volte all’anno la Terra si trova esattamente sullo stesso piano in cui il Sole gira attorno a Giove e questo fatto è molto importante. Come potete facilmente intuire, questo doppio attraversamento non dipende dall’inclinazione dell’orbita di Giove rispetto all’eclittica.

Purtroppo, questo punto è normalmente capito poco da chi cerca di spiegare in modo grossolano il fenomeno o fidandosi solo dei programmi “pappa pronta”. Mettiamoci pure nel caso più sfortunato possibile, ossia imponiamo che l’eclittica formi un angolo di 90° con il piano di Giove. Possiamo facilmente disegnare la configurazione in Fig. 27. Cosa cambia rispetto a prima. Sicuramente i due punti sopra e sotto l’orbita di Giove (T₁ e T₃) si vedono da Giove molto più distanti (prospetticamente) rispetto al Sole (se facessimo i calcoli troveremmo un valore di circa 13°), ma i punti T₂ e T₄ rimangono gli stessi, ossia continuano a coincidere con i due nodi.

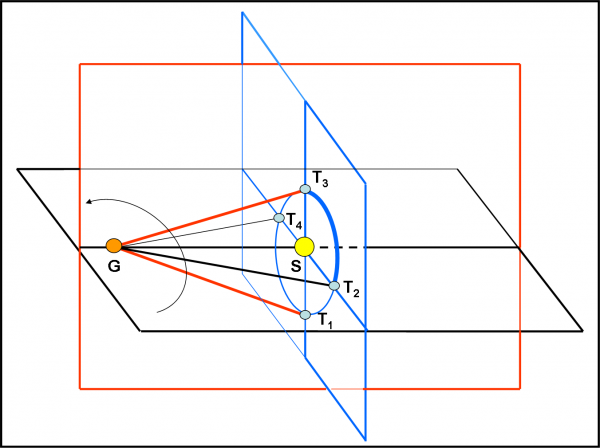
Tuttavia, è proprio ai nodi che la Terra si trova sul piano Giove-Sole e quindi in quei punti segue sicuramente le regole del Sole riguardo alla visibilità dei fenomeni tra satelliti: se il Sole vede i transiti, li deve vedere anche la Terra! Risulta chiaro che l’inclinazione dell’orbita del pianeta rispetto a quella terrestre conta ben poco ai fini della visibilità dei transiti “terrestri”. Il vero angolo fondamentale rimane sempre quello tra piano dell’orbita gioviana e piano equatoriale del pianeta gigante. Solo lui impone una visibilità dei transiti mutui (sia tra satelliti e Giove, sia tra i satelliti) più o meno continua (come abbiamo visto nei capitoli precedenti).

In ogni modo, ogni circa sei anni il Sole DEVE vedere il piano equatoriale di Giove esattamente di taglio (i nodi tra equatore e orbita). La terra segue il Sole nel suo moto, danzandogli attorno e ogni sei mesi si trova, come abbiamo visto poco fa, nel piano equatoriale di Giove. La conseguenza finale è abbastanza ovvia, ma la vedremo ancora meglio tra poco.

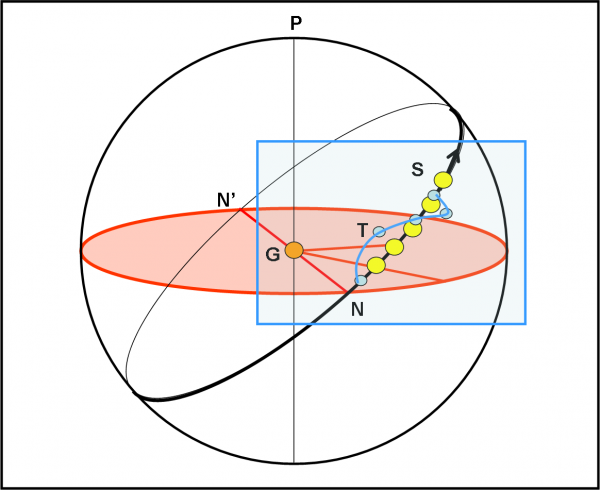
Adesso facciamo un passetto “professionale” in più e torniamo alla ben nota sfera celeste giovicentrica. La ridisegno ancora una volta (anche se ormai le diamo del “tu”…), aggiungendo solo un particolare decisamente interessante. In Fig.  28 vi è il solito cerchio massimo nero che rappresenta il percorso del Sole, che completa il suo giro in 11.86 anni. Le coordinate sono le solite declinazione e ascensione retta. L’unica differenza è che sappiamo ormai molto bene che abbastanza vicino al Sole deve sempre stare la Terra.  Come fatto precedentemente, immaginiamo che il Sole si fermi in  una certa posizione per almeno un anno. Cosa vedremo fare alla Terra se vista da Giove? Una piccola quasi-ellisse azzurra, proprio quella che abbiamo costruito poco fa.

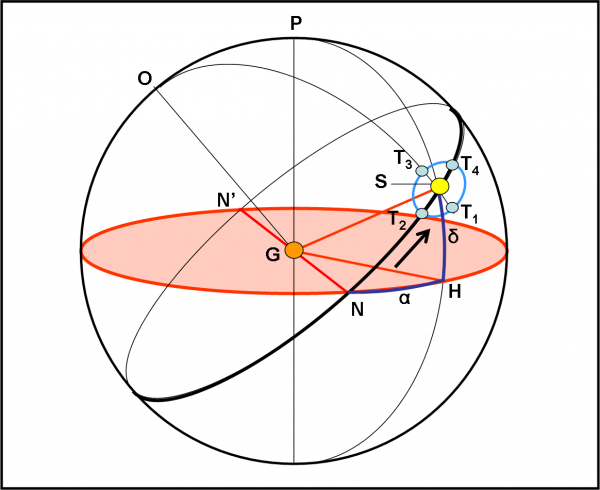
Attenzione: la possiamo costruire accuratamente e non solo qualitativamente. Infatti, gli angoli da cui Giove vede la Terra rispetto al Sole quando è nelle posizioni T₂ e T₄, li abbiamo già calcolati dai triangoli della Fig. 26. Basta disegnarli come archi lungo il cerchio massimo che passa per il Sole e per il polo O del suo piano orbitale, che è diretto, per definizione, perpendicolarmente al piano orbitale del Sole, ossia nel piano rosso della Fig. 25. Insomma, senza farla troppo lunga, è possibile calcolare perfettamente la quasi-ellisse che la Terra descrive attorno al Sole. Ovviamente, se la sappiamo descrivere nella sfera celeste giovicentrica, vuol dire che possiamo conoscere anche la declinazione e l’ascensione retta govicentriche di ogni suo punto.

Per riuscire a fare, matematicamente, questo piccolo “passo”, oltre che graficamente, è necessario applicare qualche semplice formula di trigonometria sferica. Per adesso, fidatevi di me, ma vi prometto che ci torneremo sopra e vedremo quanto è facile passare da un sistema di riferimento sferico ad un altro.

L’unico problema che abbiamo adesso dipende dal fatto che il Sole non ha nessuna voglia di stare fermo nel cielo, ma si muove costantemente, aumentando e diminuendo la sua declinazione rispetto all’equatore gioviano. Ebbene, non può certo spaventarci. Vuole dire che la Terra, oltre che descrivere la sua quasi-ellisse, si sposta di conserva con il Sole, descrivendo una specie di “sinusoide”, andando un po’ sopra e un po’ sotto alla traiettoria regolare della stella (questo fatto è veramente il punto fondamentale). A noi basta rappresentarla nella Fig. 29, in modo molto approssimato e qualitativo. Quanto basta, però, perché il solito “stupido” computer possa disegnare una traiettoria accuratissima: tutti i dati necessari glieli abbiamo già dati!

Che bello! Un’onda continua, a volte più ripida e a volte meno. D’altra parte pensate che per sei mesi la Terra viaggia nella stessa direzione del Sole, mentre per altri sei mesi si muove in direzione opposta. E’ ovvio che il risultato sia abbastanza “caotico”.

Prima di proseguire, immaginatevi questo movimento visto da Giove e mettetevi nei panni degli antichi scrutatori del Cielo. Se la situazione è così complicata quando si guarda da Giove, lo è anche quando si guarda dalla Terra e, quindi, non appare tanto strana l’introduzione degli epicicli per spiegare il moto planetario. Analogamente, potete rendervi conto della genialità di chi è riuscito, a spiegare tutto mettendo il Sole al centro e addirittura a scrivere le leggi orbitali. Non parliamo poi di chi ha capito che era tutto legato a una legge universale! Va beh… torniamo a noi.

Nella Fig. 29 ho disegnato un riquadro azzurro e lo riporto ingrandito nella Fig. 30, dove per diversi punti ho evidenziato le declinazioni e le ascensioni rette del Sole e della Terra. Inoltre, ho anche accoppiato le posizioni assunte dal Sole e della Terra nello stesso istante t. In tale modo, oltre alle coordinate giovicentriche, riusciamo anche a rappresentare il tempo che scorre. Non confondiamo, infatti, il tempo con l’ascensione retta. In un certo istante, Terra e Sole possono assumere, ovviamente, posizioni diverse. Analizziamole più attentamente, partendo dal basso a sinistra.

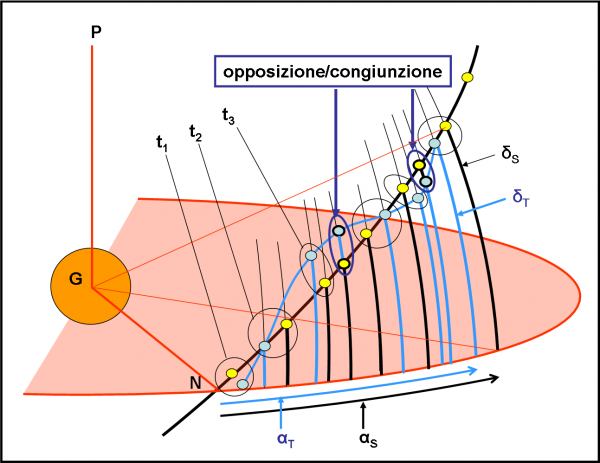
La prima coppia rappresenta il Sole la Terra poco dopo che il Sole è passato dal nodo ascendente N. Fortunatamente (state bene attenti a quello che dico!), la quasi ellisse del Sole è molto piccola e quindi la Terra deve sempre essere molto vicina al Sole, anche nel momento in cui lui è passato al nodo. Questo fatto implica che se i transiti sono visti dal Sole, lo sono anche dalla Terra. Il ogni modo, il Sole rimane abbastanza a lungo vicino al nodo, a sufficienza perché la Terra, anche con un’orbita più inclinata (ossia con una quasi-ellisse molto più allungata verso l’alto e verso il basso), riesca a passare nel suo moto attorno al Sole da declinazioni negative a positive e/o viceversa. Questo è il punto fondamentale! Passare da declinazioni negative a positive vuole dire attraversare l’equatore di Giove, ossia il piano dei satelliti e, quindi, vedere i loro piani orbitali di taglio (o quasi)!

In altre parole: condizione essenziale perché la Terra possa vedere i transiti dei satelliti su Giove (e tra di loro) è che la sua traiettoria apparente vista da Giove tagli il suo piano equatoriale. Dato che il Sole lo fa almeno una volta ogni sei anni e che la Terra gli gira attorno ne segue che anche il nostro pianeta è obbligato a farlo. Queste sono le uniche condizioni che permettono i transiti mutui tra satelliti! Pensateci bene e vi apparirà una conclusione di un’ovvietà quasi ridicola: altro che essere un problema per soli professionisti.

L’inclinazione piccola dell’orbita gioviana, rispetto a quella terrestre, implica soltanto che i transiti visti dal Sole e quelli visti dalla Terra capitino praticamente nello stesso periodo di tempo. Se l’orbita terrestre fosse più inclinata e/o descritta in un  periodo più lungo di un anno, i transiti solari e quelli terrestri potrebbero avvenire in tempi anche abbastanza diversi. Provate a pensarci sopra e vedrete che la faccenda è molto semplice. Vi do un aiuto. Se il periodo fosse più lungo, la sinusoide della figura precedente si allungherebbe e quando il Sole si trova al nodo N (o lì vicino), la Terra potrebbe trovarsi molto distante da quel punto e quindi non vedere i transiti. Idem, se si spostasse troppo verso l’alto o verso il basso. Tuttavia, lo ripeto ancora una volta, prima o poi la Terra sarebbe comunque obbligata ad attraversare l’equatore di Giove e assisterebbe tranquillamente ai transiti mutui dei satelliti. Tutta questa attenzione riguarda solo i transiti mutui tra i satelliti e non i transiti dei satelliti sul disco di Giove. In questo secondo caso i paralleli di visibilità sono molto più “permissivi” e permettono di allontanarsi molto di più dai nodi dell’equatore di Giove.

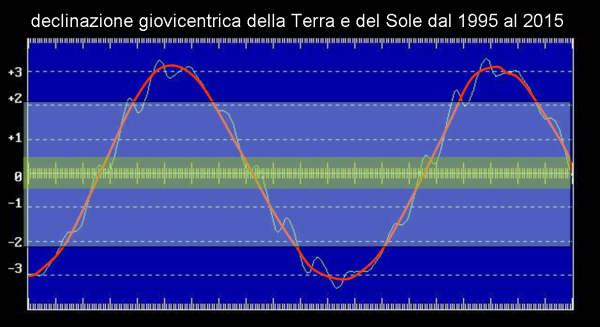
Potevamo risolvere la questione in modo ancora più sbrigativo, senza tante parole. Bastava che nella Fig. 29 avessimo disegnato i paralleli azzurri che limitano la visibilità dei transiti su Giove e tra satellite e satellite, ossia riportarci alle figure adottate negli articoli precedenti. E’ proprio quello che facciamo adesso. Anzi, andiamo oltre e consideriamo il diagramma che descrive la declinazione giovicentrica del Sole in funzione del tempo, aggiungendo alla declinazione del Sole anche quella della Terra, con la sua strana curva che continua a danzare attorno a quella regolare del Sole.

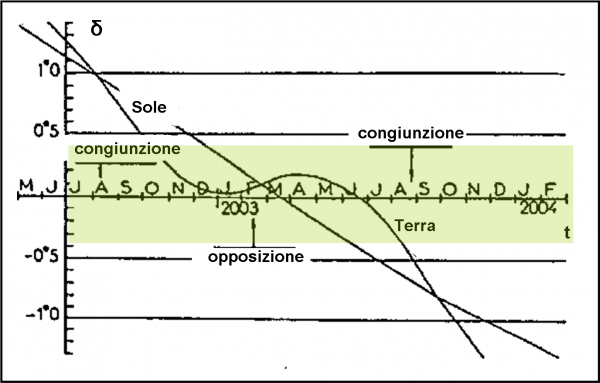
Lo rappresentiamo nella Fig. 31, dove abbiamo inserito sia la fascia azzurra (relativa alla visibilità di transito di tutti i satelliti su Giove) sia quella verde (relativa alla visibilità di almeno un transito mutuo tra i satelliti). Insomma, abbiamo ripetuto la Fig. 22,  aggiungendovi la traiettoria giovicentrica della Terra. Un gioco veramente da ragazzi che ci permette di stabilire subito quando e come si verificano sia i transiti rispetto al Sole “acceso” (eclissi se visti dalla Terra) sia rispetto alla stessa Terra (osservatore passivo).

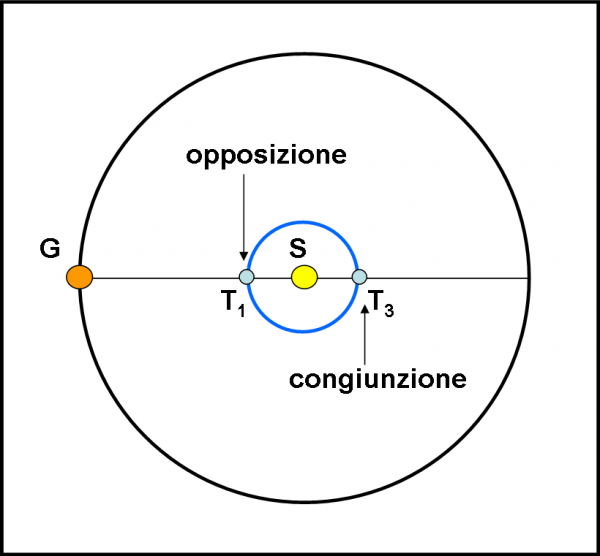
Torniamo ancora un attimo alla Fig. 30. Nella traiettoria Sole-Terra vi sono altri punti particolari. Li ho indicati come congiunzioni/opposizioni. Essi sono gli istanti  in cui l’ascensione retta del Sole e della Terra sono uguali. Ciò può essere possibile in due casi, che avevo già descritto nell’articolo sulle opposizioni… L’opposizione si ha quando il Sole e Giove si trovano a 180° l’uno dall’altro, La congiunzioni quando Sole e Giove sono entrambi nella stessa direzione. Viste da Giove entrambe le configurazioni danno, ovviamente, la stessa ascensione retta sia per la Terra che per il Sole. La situazione, molto schematizzata e vista dall’alto (non considerando, quindi, l’inclinazione orbitale) è riportata in Fig. 32. E’ facile intuire che per le osservazioni sono molto più convenienti le opposizioni, dato che Giove si vede di … notte.

Siamo proprio arrivati alla fine. Possiamo concludere con la figura più tecnica che nasce spontaneamente dal nostro lento avvicinamento. La Fig. 33 riporta il periodo dei transiti e delle eclissi mutue tra satelliti gioviani nel periodo 2003-2004. La zona verde è quella che già conosciamo bene ed è relativa alla visione di almeno il transito mutuo tra Io ed Europa. Come vedete per un certo numero di mesi sono visibili sia i transiti mutui tra satelliti (curva sinusoidale della Terra) sia le eclissi mutue (curva regolare del Sole).

Siamo riusciti, con carta e matita, a ricostruire un po’ alla volta il diagramma professionale che illustra le condizioni ideali per osservare, con gli strumenti più adatti (normalmente i fotometri fotoelettrici come fa Kepler), i fenomeni mutui tra i satelliti di Giove. Un diagramma è comunque sempre e solo un diagramma. Per pianificare le osservazioni bisogna riferirsi alle tabelle che danno con grande precisione gli istante di inizio e fine dei vari fenomeni. A produrre queste tabelle ci pensano, ovviamente, i soliti “schiavi” elettronici.

A questo punto, si può anche utilizzare celestia & co., per vedere sullo schermo la stessa cosa che noi siamo riusciti a disegnare da soli. Si può anche fare… ma non penso che possa più dare alcuna soddisfazione. Chi è interessato veramente a osservare gli eventi deve, comunque, riferirsi alle tabelle. Chi, invece, è interessato al come e perché, trova tutte le risposte solo attraverso il ragionamento e non certo con una “pappa pronta” che spiega poco o niente. Insomma, celestia e i suoi fratelli, o eventuali migliorie personalizzate, non servono a nessuno, né agli osservatori né agli amanti delle regole del Cosmo!

Concludo con una constatazione e un invito per chi avesse tempo e voglia. La trattazione che abbiamo seguito non vale certamente solo per Giove, ma per qualsiasi sistema satellitario. Basta cambiare i parametri orbitali e si ottengono TUTTE le figure ricavate per Giove. Anzi, vi dirò di più: i casi di Saturno e dei pianeti esterni (possiamo anche considerare l’ex Plutone) sono decisamente più favorevoli, dato che l’orbita della Terra, vista da loro, diventa ancora più stretta e gli angoli di vista diminuiscono. Inoltre, abbiamo il caso molto interessante di Urano. Il suo piano equatoriale forma un angolo di circa 90° con il piano orbitale. Qualche problema?  Nessuna paura: il Super Kepler Sole sa benissimo che anche in questo caso peculiare ci sono sempre e comunque due punti sempre sicuri, ossia i nodi… Divertitevi se volete…

Ancora una cosa… Non pensate che tutta questa lunga serie di articoli sia servita solo ai satelliti dei pianeti e ai loro fenomeni mutui. E’ servita a introdurre le coordinate sferiche e a spostarle da un oggetto a un altro, cambiando piano di riferimento.  Potrebbe essere arrivato il momento di spiegare nel modo giusto e con le dovuta accuratezza i vari sistemi di coordinate e la matematica che permette di eseguire le trasformazioni. L’astronomia ha assoluto bisogno della trigonometria sferica e ormai siete in grado di affrontarla (sempre che non la conosciate già). Se siete d’accordo lo faremo quanto prima. Ancora una volta vedrete che le vere difficoltà sono tutta un’altra cosa. Quindi, vi prego di digerire bene questi sei capitoli. Mi fido di voi…