In questa parte, veramente fondamentale, calcoliamo la prima derivata di una funzione che non sia una retta e ne diamo il significato geometrico. Lo scenario si amplia sempre di più.

Prendiamo subito di petto il calcolo di una derivata che non sia quella un po’ troppo banale della retta. Consideriamo l’equazione della parabola più semplice, ossia:

y = f(x) = x²

Calcoliamone il rapporto incrementale

(f(x + h) –f(x))/h = ((x+h)² – x²)/h = (x² + h² +2xh – x²)/h = h(2x + h)/h = 2x + h

E poi passiamo al limite per h che tende a zero:

y’ =  f ‘(x) = lim _h→0 (2x + h) =  lim _h→0 2x + lim _h→0 h = 2x + 0 = 2x    … (1)

Non abbiamo fatto altro che utilizzare il quadrato di un binomio e le operazioni sui limiti (cose già trattate…).

y’ = f ’(x) = 2x è una nuova funzione. Ma la conosciamo bene: è una retta! Attenzione non sarà sempre una retta e quindi non confondiamoci fin dall’inizio. E’ una retta nel caso della parabola. Tuttavia, ricordiamoci questo “strano” legame: la retta è un polinomio di primo grado e la derivata è una costante. La parabola è un polinomio di secondo grado e la derivata è di primo grado.

Sospendiamo questo discorso, lo riprenderemo presto. In ogni modo, possiamo dire che la derivata della parabola, al variare di x, descrive una retta, ossia cresce regolarmente al crescere di x. Ma la derivata non significa altro che la variazione di y al variare di x. Quindi, qualitativamente, il risultato ottenuto per la parabola (1) ci dice che, a mano a mano che x cresce, la variazione istantanea della y cresce anch’essa seguendo la legge rettilinea espressa dalla funzione derivata y’ = 2x.

Possiamo calcolare questa variazione istantanea punto per punto? Sicuramente sì, dato che abbiamo l’equazione della funzione che la rappresenta (in questo caso la retta y’ = f’(x) = 2x).

Basta, perciò, sostituire x con un valore particolare x₀ nella y’ = 2x e ottenere subito il valore della f’(x₀) = 2x₀. Ad esempio:

Per il punto di ascissa x₀ = 1/2                      f ’(1/2) = 2·1/2 = 1

Per il punto di ascissa x₀ = 1                         f ’(1) = 2·1 = 2

Per il punto di ascissa x₀ = 5                         f ’(5) = 2·5  = 10

E per il punto x₀ = 0                                      f ’(0)   = 2·0  =   0

Abbiamo dato solo dei numeri. Interessanti sì… ma solo dei numeri, senza alcun significato geometrico o fisico. Ma ne siamo proprio sicuri?  Torniamo un attimo indietro… Quando abbiamo trovato la derivata della funzione retta, abbiamo visto che la derivata è una costante, che è anche il coefficiente angolare della retta stessa.

In qualche modo, con l’operazione di derivazione abbiamo trovato il coefficiente angolare di una retta che, in quel caso, coincide con la funzione retta di partenza. E se fosse un caso ben più generale? In altre parole, e se la derivata calcolata in un punto di una qualsiasi funzione fosse proprio il coefficiente angolare di una certa retta legata a quel punto? Sarebbe bello, accidenti! Sì, ma che retta sarebbe?

Non è mica tanto difficile arrivarci… Basta riprendere in mano il metodo con cui abbiamo definito il rapporto incrementale e poi il suo limite per h che tende a 0, ossia per x che tende a x₀. Cerchiamo di costruirci questa retta veramente speciale attraverso la geometria. Usiamo, per una migliore spiegazione, proprio la nostra parabola. Consideriamo un suo punto P qualsiasi di ascissa x₀.

Spostiamoci un po’ rispetto a questa ascissa e disegniamo il punto Q che ha ascissa x = x₀ + h. La Fig. 77 ci indica chiaramente il rapporto incrementale attraverso il triangolo PQH. E sì, care ragazze e ragazzi, è sempre il vecchio e buon triangolo rettangolo che ci è servito un mucchio di volte. Il rapporto dei suoi cateti è proprio il rapporto incrementale e l’angolo opposto al cateto QH è l’angolo α la cui tangente trigonometrica è proprio il coefficiente angolare della retta individuata da PQ. Direi che su questa conclusione non ci sono dubbi. In caso contrario, andate a rivedervi rapidamente il significato di coefficiente angolare… ma ormai dovreste averlo capito molto bene.

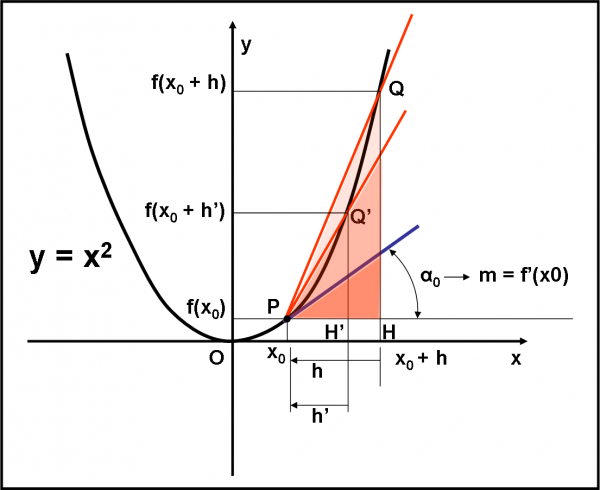
Bene, abbiamo stabilito un fatto importantissimo (che avevamo già visto nel caso particolare della derivata di una retta, ricordate?): il rapporto incrementale costruito per qualsiasi funzione (noi usiamo la parabola, ma potremmo usare qualsiasi altra funzione) è il coefficiente angolare della retta che passa per il punto P e per il punto corrispondente a x₀ + h, ossia Q. A questo punto non ci resta che passare al limite per h che tende a zero, ossia per x che tende a x₀.

Graficamente, questa operazione vuole dire spostare H (e quindi anche Q) verso P. Fermiamoci un attimo, ad esempio, quando siamo arrivati in H’ e Q’. Come previsto la retta PQ è cambiata e adesso è PQ’. Mentre nel caso della funzione retta questa operazione manteneva costante il rapporto incrementale, questa volta esso cambia perché è cambiato l’angolo α (adesso è diventato α’) e, quindi anche il coefficiente angolare. In poche parole, è cambiata la pendenza della retta PQ’ rispetto a quella di PQ.

Attenzione, ripetiamoci ancora:  qual è la differenza rispetto al rapporto incrementale della funzione retta? Solo e soltanto che in quel caso m non variava mai, dato che Q si muoveva proprio lungo la retta di partenza.

Torniamo a noi, dato che H (e Q) scalpitano e vogliono arrivare a coincidere matematicamente con P, ossia h vuole diventare ZERO. Lasciamoli liberi di agire, tanto ormai abbiamo capito cosa succede. La retta PQ’ cambia ancora e continuamente fino a che il “vecchio” Q coincide con P. A questo punto, che succede? la retta è sparita, volatilizzata? Neanche per sogno dato che il rapporto incrementale, ossia il coefficiente angolare esiste ancora e come! Anzi, quando Q tocca P esso diventa proprio la derivata in quel punto!  Ecco che cosa rappresenta la derivata di una funzione in un punto. Nient’altro che il coefficiente angolare m di una retta che forma un angolo α₀ con l’asse delle x. E’ facile tradurre tutto in una banale formula:

m = tan(α₀) = f ’(x₀) = 2x₀

Questa retta è, quindi, facilmente tracciabile, ma non sappiamo ancora dove disegnarla.

Sciocchezze! Deve per forza passare sia da P che da Q che ormai coincidono! Che retta particolare è mai questa? Attenzione al seguente ragionamento:

Essa è una retta che tocca la funzione parabola in P, ma che NON può avere altre intersezioni con la parabola nell’intervallo QP di partenza, altrimenti vorrebbe dire che h non è ancora arrivato a zero. Bene questa retta non è altro che la tangente alla curva parabola nel punto P.

Ne segue come ovvia conclusione che la derivata rappresenta il coefficiente angolare della tangente al punto P della curva. Meraviglioso, non credete? Vedrete che fantastiche applicazioni ha questo risultato geometrico!

Prima di proseguire nel mondo delle derivate che ormai ci ha aperto una porta enorme, fermiamoci a riflettere sulla tangente a una curva.

Tutti voi conoscete cos’è la tangente a una curva (fuggire per la tangente è un modo di dire di uso comunissimo), ma sapreste darne una definizione esatta? Sembrerebbe facile, ma non è così ovvio, anzi. C’è proprio voluta la geometria differenziale e il concetto di limite per poterla descrivere e definirla. Spesso si trova scritto che la tangente a una curva in punto P è la posizione limite, se esiste, della secante PQ al tendere di Q a P. In altre parole, esattamente ciò che abbiamo fatto poco fa per definire la derivata.  In effetti, proprio la definizione di derivata definisce la tangente a una curva qualsiasi. La tangente è quindi una retta che ha bisogno del concetto di limite. Non è quindi una figura veramente fisica, ma solo un concetto matematico.

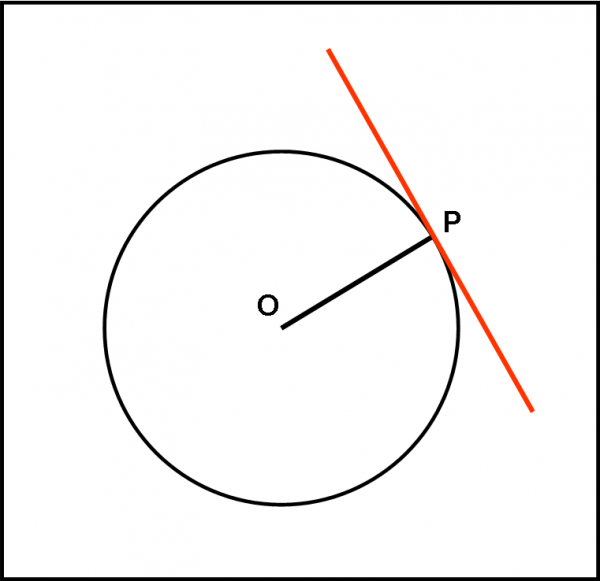
State bene attenti a quello che dico perché può sembrarvi un assurdità. In realtà, NON esiste la tangente a una curva, ma esiste solo la tangente a una circonferenza in P. Solo nel caso della circonferenza è facile definirla come la perpendicolare alla congiungente il centro della circonferenza con il punto P. Una definizione, quest’ultima, che porta a un’immediata soluzione senza bisogno di passaggio al limite o di un qualcosa di particolare. Preso un punto P qualsiasi, basta tracciare la congiungente OP e quindi disegnare la perpendicolare a questo segmento passante per P, come rappresentato in Fig. 78. La fisica, quindi, avrebbe bisogno di una circonferenza e non di un limite… Tuttavia, la faccenda si risolve abbastanza bene attraverso un compromesso che fa uso del cerchio osculatore.

Il cerchio osculatore a una curva in un suo punto P è quel cerchio che meglio approssima  la curva attorno al punto P. Quel “meglio” sa tanto di fisico. Permette, infatti di fermarsi nel momento che preferiamo, senza bisogno di usare microscopi sempre più potenti. A seconda di ciò che si vuole ottenere ci si può fermare ad un certo punto nell’approssimazione matematica di una curva nell’intorno di un punto.

Vi faccio un esempio. Disegniamo un cerchio e poi cerchiamo di approssimarlo con una figura lineare, ossia senza curve. E’ la famosa quadratura del cerchio di cui abbiamo parlato introducendo la spirale di Archimede. Se partiamo da un quadrato, il risultato sarà ben modesto e insufficiente. Molto meglio prendere un esagono. Meglio ancora un ottagono e via dicendo fino a considerare un poligono regolare con centinaia e centinaia di lati. In quest’ultimo caso si potrebbe dire che un archetto di cerchio è quasi perfettamente approssimato dalla corda che lo sottende. Spesso in fisica si fa così e si sostituisce un arco piccolissimo di cerchio con un segmento lineare, senza commettere errori importanti. Per la nostra curva è un problema simile.

In prima approssimazione, potremmo considerare proprio la tangente intorno al punto P come rappresentazione della curva. Ma, ancora meglio sarebbe utilizzare un cerchio che tocca la curva in P. Volendo si potrebbe anche utilizzare una curva ancora più elaborata, ma va al di là degli scopi normali. Mi basta anticiparvi un concetto che tornerà utile (e che in parte conosciamo). Per migliorare la curva che approssima una curva qualsiasi basta aumentare il grado di una funzione espressa come polinomio. Se il grado è uno, abbiamo la retta, se è due abbiamo la parabola o una sua sorella conica, se il grado è tre… va beh… lo vedremo più in là.  Tuttavia, abbiamo imparato che si ha un’approssimazione migliore facendo crescere il grado del polinomio che approssima la curva, e quindi si comprende anche la frase: “approssimazione di grado superiore”. Per quanto ci riguarda, accontentiamoci del cerchio osculatore.

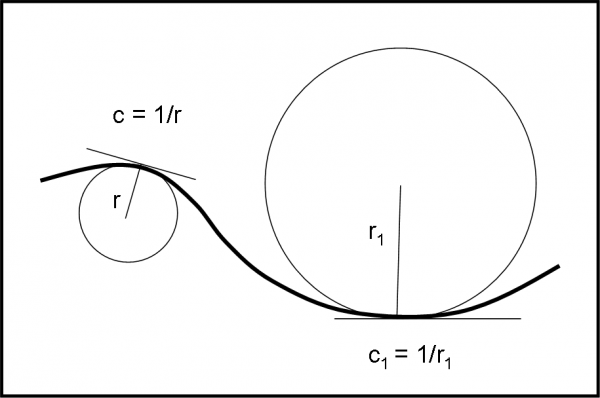
Ebbene, la tangente a una curva in punto P può definirsi anche come la tangente al cerchio osculatore nel punto P. Sembrerebbe un’inutile forzatura. E, invece, in fisica è molto importante. Non possiamo andare nei dettagli, ma pensate solo che introdurre un cerchio vuol dire sapere anche qual è il suo raggio e qual è la sua curvatura (l’inverso del raggio). Se pensate alle forze centripete e alla curvatura dello spazio, non vi sarà difficile avere una vaga idea dell’importanza del cerchio osculatore di una curva qualsiasi in un suo punto qualsiasi. Ne vediamo un esempio in Fig. 79.

Torniamo, però, alla nostra derivata, che ci ha svelato un suo risvolto eccezionale. Non ci resta che giocare assieme a lei e applicarla in tutti i modi possibile. Cerchiamo di farla diventare come il prezzemolo!

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica