Cominciamo a calcolare alcune derivate di funzioni particolari, rappresentate dai semplici monomi. Una rapida analisi dei risultati ci insegna che esiste una facile regola generale che evita il noioso passaggio attraverso il rapporto incrementale. Segue un’appendice per i più … volenterosi.

Iniziamo da una funzione che abbiamo già visto nei capitoli sulle coniche.

y = 1/x    (che è poi l’equazione più semplice di un’iperbole)

Costruiamo il rapporto incrementale:

(1/(x + h) - 1/x)/h = (x – x – h)/((x+h)x/h) = - h/(x+h)xh = - 1/(x+h)x

E poi facciamone il limite per h che tende a zero per ricavare la derivata y’:

y’ = lim _h→0 (-1/(x+h)x) = lim _h→0  (-1)/ lim _h→0 (x+h)x = -1/(lim _h→0 x + lim _h→0 h) lim _h→0 x =
= -1/(x + 0) x = -1/x² = - x^-2

Abbiamo fatto parecchia fatica… non c’è che dire e abbiamo anche dovuto ricordarci le operazioni con i limiti (niente di speciale dato che valgono le regole normali di somma, differenza, prodotto e divisione). Eh sì, calcolare sempre il rapporto incrementale rischia veramente di farci dimenticare qualcosa per strada o commettere qualche  errore di scrittura. Non parliamo poi di quando le funzioni si complicano ancora di più… Bisogna trovare una qualche regola più semplice per calcolare le derivate.

Facciamo ancora uno sforzo e proviamo con

y = x³

per ricavare questa derivata bisogna ricordarsi quanto vale il cubo di un polinomio. Se non ve lo ricordate, andate a rivederlo…

Scriviamo il solito e noioso rapporto incrementale:

((x + h)³ – x³)/h = ((x³ +3x²h + 3xh² + h³) – x³ )/h = (3x²h + 3xh² +h³)/h = (3x²+ 3xh +h²)h/h =
= 3x² + 3xh + h²

Non ci resta che passare al limite per h che tende a zero. Tuttavia, permettetemi di sveltire un po’ i passaggi, sapendo già che il limite di una somma è la somma dei limiti, il limite di un prodotto è il prodotto dei limiti e il limite di una costante (rispetto ad h) è la stessa costante:

lim _h→0 (3x²+ 3xh + h²) = 3x² + 0 + 0 = 3x²

Ce l’abbiamo ancora fatta abbastanza facilmente… ma che succederebbe se dovessi elevare alla quarta o quinta potenza la x? Mamma mia… sarebbe, se non altro, una bella noia. E se dovessi fare delle radici quadrate o cubiche? Meglio non pensarci…

Cerchiamo di usare il cervello e riscriviamo quelle poche funzioni di cui abbiamo ricavato la derivata. Poi ragioniamoci sopra

y = 1 = x⁰

y = x

y = x²

y = x³

y = 1/x = x^-1

In fondo, sono tutte funzioni composte da un monomio, in cui cambia solo il grado (ossia l’esponente della x). Anche la prima lo è, dato che possiamo scrivere 1 come x⁰.

Richiamiamo le loro derivate che abbiamo calcolato precedentemente. In realtà ci manca quella di x⁰, ma la possiamo ricavare immediatamente con un semplice ragionamento (non vi è bisogno di costruire il rapporto incrementale). Sappiamo che scrivere y = costante (1 è una costante) vuol dire scrivere l’equazione di una retta parallela all’asse x. Ma se è una retta, sappiamo già che la sua derivata è il coefficiente angolare della retta. Qual è il coefficiente angolare di una retta parallela all’asse x? Per definizione deve essere zero, dato che l’angolo α è zero e tale deve essere anche la sua tangente trigonometrica. Se ne conclude che la derivata di una costante deve essere ZERO. E lo è qualsiasi sia la costante… sia 1 che un qualsiasi numero n (perfino 0, dato che y = 0 è proprio l’equazione dell’asse x).

Ecco, allora, la tabella comparativa

y                            y’

x⁰                          0

x¹                          1

x²                          2x

x³                          3x²

x^-1                       - x^-2

Qualche strana corrispondenza c’è sicuramente. Ma la vediamo meglio se scriviamo le derivate in modo ancora più “completo”

y                            y’

x⁰                          0x^-1   (potevo scrivere qualsiasi cosa, dato che il risultato è sempre zero…)

x¹                          1x⁰

x²                          2x

x³                          3x²

x^-1                        -1x^-2

La relazione tra funzione e derivate è ormai evidente… mi posso permettere di scrivere subito la derivate di altre due funzioni dello stesso tipo:

y = x⁴

e

y = 1/x² = x^-2

La prima vale sicuramente:

y’ = 4x³

e la seconda:

y’ = -2x^-3

Come ho fatto? Semplicissimo! Ho capito come funziona la regola per passare da funzione a derivata (quando abbiamo a che fare con un monomio, ovviamente).

Cosa si deve fare? Prendere l’esponente a cui è elevata la x e moltiplicarlo per la x elevata all’esponente di prima meno uno, ossia abbassare di uno il grado del monomio e moltiplicarlo per l’esponente iniziale.

In parole matematiche e molto più chiarificatrici:

se

y = xⁿ

vale sempre:

y’ = n x ^n-1         … (1)

Questa regola vale anche per n negativo (come abbiamo già visto) e per n frazionario (ossia per le radici). Applicate la regola a tutte le funzioni di prima e vedrete che ho proprio ragione! Insieme scriviamo invece la derivata di una radice, ad esempio

y = √x = x^½

Scommetto che avete già capito tutto…

y’ = ½ x ^{(½ - 1)} = ½ x^{- ½}  = 1/2x^½= 1/2√x

il risultato sembra strano, ma avete visto che l’ho ottenuto esattamente con regola (1).

Siamo riusciti a trovare un unico metodo per calcolare le derivate di qualsiasi monomio, qualunque sia il suo esponente (grado). E il metodo vale anche se la x sta a denominatore (esponente negativo) o se è sotto radice (quadrata, cubica o quello che volete), ossia se l’esponente è frazionario.

Vi rendete conto di quello che abbiamo in mano? Per qualsiasi funzione di questo genere siamo in grado di calcolare la funzione derivata (come vedete è una funzione che può essere di qualsiasi grado) e, di conseguenza, sostituendo l’ascissa di un punto qualsiasi della funzione di partenza, ottenere la tangente alla curva in quel punto. Pensateci sopra e vi accorgerete che è una conquista matematica e geometrica enorme.

Fate pure tutte le prove che volete per prendere dimestichezza. Anzi, vi do qualche esercizio…

Calcolate la derivata delle seguenti funzioni:

y = x⁷

y = 1/x⁴

y = √x³

y = 1/(³√x²)

Le prime due sono facilissime… le ultime due, forse, vi impegneranno di più… ma la regola è sempre la stessa! Nell’ultima la scrittura “ ³√ ” vuol dire radice cubica. Potevo scriverla in altro modo, ma vi avrei già aiutato troppo…

Fermiamoci qui, ma vi annuncio che la prossima volta inizieremo a fare le operazioni con le derivate…

APPENDICE (per i più esperti e/o volenterosi): un aperitivo prima dello studio di una funzione

Anche se siamo solo all’inizio dello studio delle derivate, quanto sappiamo ci permette già di fare un “piccolo” studio di funzione o -quantomeno- di vedere come la conoscenza delle tangenti in un qualsiasi punto della curva ci permetta di capire l’andamento della funzione e di come si comporti all’infinito in modo più “raffinato”. Chi non se la sente, non abbia paura: ci torneremo sopra più lentamente e con spiegazioni più estese. Chi, invece, vuol provare, si divertirà sicuramente nel capire quante cose, ancora nascoste, la derivata può svelare.

Cerchiamo di disegnare due funzioni abbastanza semplici e comuni. Lo potremmo fare per punti (svuotare il mare con il cucchiaino), ma, invece, preferiamo calcolare la derivata in pochissimi punti (ossia definire la tangente alla curva in quei punti) per avere subito un’idea di massima delle funzioni.

Cominciamo con

y = x³

la cui derivata è:

y’ = 3x²

Prendiamo qualche punto sia dalla parte positiva che da quella negativa dell’asse delle ascisse e calcoliamo in quei punti sia la y che la y’.

x = 0                y = 0              y’ =  0

x = 1                y = 1               y’ = 3

x = 2                y =  8              y’ = 12

x  = +/- ∞       y = +/- ∞        y’ = + ∞

x = - 1              y = - 1            y’ = 3

x = - 2              y = - 8            y’ = 12

Con questi dati possiamo facilmente disegnare una figura in cui nei vari punti P(x,y)  appena identificati, si può tracciare la tangente relativa, ossia la retta che è tangente in quei punti alla curva e che ha come coefficiente angolare la derivata. Ricordiamoci che, sapendo il coefficiente angolare m di una retta, si disegna immediatamente la retta dato che la sua direzione è quella dell’ipotenusa di un triangolo rettangolo che abbia come rapporto dei cateti proprio il numero m, ossia:

Δy/Δx = m     … (2)

Praticamente, perciò, basta disegnare un cateto uguale a 1 e l’altro uguale a m. Infatti, se nella (2) poniamo Δx = 1, otteniamo immediatamente Δy = m. In parole ancora più povere, se m fosse uguale a 3 otterrei questo numero sia da rapporti come 72/24, 27/9, 9/3, … ma anche da 3/1. Dato m è immediato quindi disegnare la retta che ha quel coefficiente angolare senza bisogno di introdurre angoli e tangenti di angoli. Una volta trovata la direzione, basta spostarla parallelamente a se stessa fino a passare per il punto P. Tante parole, ma è tutto semplicissimo guardando la Fig. 80.

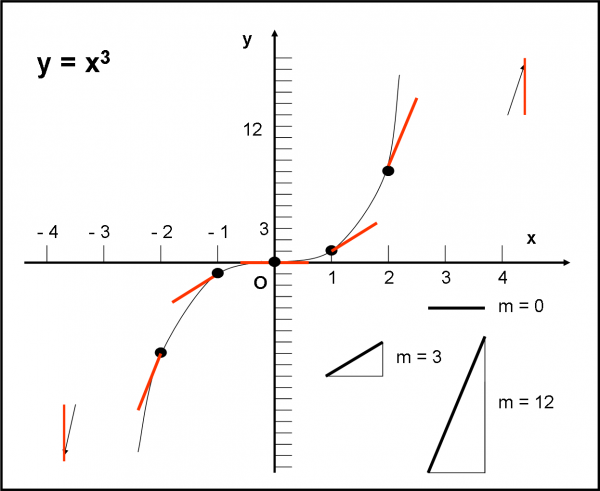
La prima cosa da fare è disegnare subito i punti P(x,y). Sono tutti immediati, compresi quelli all’infinito che indichiamo con una freccia. In basso, a destra, vi sono i triangoli rettangoli che ci servono a tracciare la direzione delle varie tangenti che hanno y’ come coefficiente angolare. Queste rette  le trasporto poi nei punti corrispondenti appena disegnati (rette rosse).

Permettetemi una piccola complicazione che serve solo a rendere più comprensibile la curva finale. Uso scale diverse per le ascisse e per le ordinate. Per non fare diventare la curva troppo “stretta”, l’unità delle x è cinque volte maggiore di quella delle y. Ossia se x =1 equivale a 1 cm, y = 1 equivale a 1/5 di centimetro. Abbiate pazienza, ma è uno sforzo aggiuntivo necessario…

La figura spiega da sola molte cose. La curva passa dall’origine degli assi e la sua tangente in quel punto è proprio l’asse delle x. Notate che bell’onda compie intorno a quel punto… Sembra proprio che si “fletta” … Più interessante ancora, anche se meno intuitivo, è ciò che capita ai punti all’infinito. Dalla funzione sappiamo che per x che tende a infinito anche la y deve tendere a infinito (più infinito a destra e meno infinito a sinistra). Tuttavia, sappiamo anche che la tangente alla curva nel punto all’infinito ha coefficiente angolare ∞. Cosa vuol dire questo risultato? Beh… il coefficiente angolare non è altro che la tangente trigonometrica dell’angolo che la retta forma con l’asse delle x. Dalla trigonometria sappiamo, però, che, per avere una tangente trigonometrica che vale infinito, l’angolo deve essere 90°, ossia la tangente del punto all’infinito della curva è parallela all’asse delle y. Attenzione, attenzione… ciò non vuol dire che la curva ha un asintoto per x che tende a infinito (in questo caso avremmo che per x che tende a infinito la y tende a un numero finito), ma dice qualcosa di veramente al di fuori del nostro modo di pensare. In quello strano mondo dei punti all’infinito, quello della nostra curva ha una tangente verticale… Un concetto non facile, ma che acquista importanza enorme nello studio del piano ampliato… Lasciamolo pure da parte, ma  ci da un segnale di quanto sia veramente “complessa” la matematica portata ai suoi militi estremi.

Passiamo all’altra funzione:

y = √x

la cui derivata è:

y’ = 1/(2√x)

Questa curva ha un gran vantaggio: esiste solo nella zona positiva delle x. Infatti, non esiste la radice quadrata di un numero negativo. Se ci fosse vorrebbe dire che il quadrato di un certo numero sarebbe negativo. E questa è un’assurdità (almeno se non si entra nel mondo dei numeri immaginari…). Inoltre, possiamo tranquillamente usare la stessa scala per le x e per le y, dato che i valori assunti sono comparabili. Calcoliamo, come prima, le coordinate di qualche punto e le derivate  corrispondenti.

x = 0               y = 0                 y’ = + ∞

x = 1               y = 1                 y’ = 1/2 = 0.5

x = 2               y = 1.41            y’ = 1/(2 · 1 .41) = 0.35

x = + ∞           y = + ∞             y’ = 0

Ho scritto 1,41 come valore della √2, anche se i decimali continuano… Tuttavia, per disegnare una figura, basta e avanza… Come per la figura precedente, calcoliamo la direzione delle tangenti utilizzando il solito triangolo rettangolo. Disegniamo i risultati nella Fig. 81.

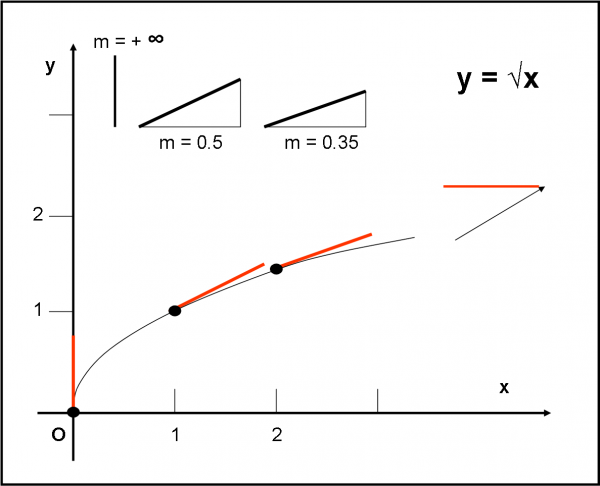
La derivata nell’origine degli assi vale infinito e quindi la tangente non è altri che l’asse delle y. Poi la tangente continua a diminuire la sua pendenza. Quanto vale al punto all’infinito della curva? Proprio zero, ossia è parallela all’asse delle x. Ma NON è l’asse delle x, dato che deve passare per il punto all’infinito, ossia per il punto che ha coordinate P(∞,∞), dato che sappiamo bene che per x che tende a infinito anche la y deve tendere a infinito. Tuttavia, in quel punto “assurdo” la tangente alla curva è orizzontale.

Confrontiamola con il caso precedente. Anche quella curva tendeva a un punto P(∞,∞), ma la sua tangente era parallela all’asse delle y. Qui, invece, la tangente è orizzontale. Come possiamo anche esprimere questo concetto un po’ complicato, a prima vista? Nel caso y = x³ la tangente alla curva (ossia la derivata) tende a diventare una retta parallela all’asse delle y, per x che tende a infinito. Nel caso y = √x, la tangente tende a essere una retta parallela all’asse x per x che tende a infinito. D’altra parte, non è un risultato tanto strano, dato che le due derivate y’ sono anch’esse funzioni di x e quindi è facilissimo calcolarne il limite per  x che tende a infinito.

Non abbiamo ottenuto niente di straordinario, ma ci siamo divertiti a vedere quanti giochi di prestigio si possono fare con le derivate (e siamo ancora alla derivata prima…). Ma sono giochi che hanno grandi applicazioni in fisica. Basterebbe pensare al campo gravitazionale e all’energia gravitazionale su un punto che tende a infinito.

Torniamo a cose più pratiche e “normali”…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica