Categorie: Meccanica Celeste Sistemi extrasolari
Tags: 55 Cnc esopianeti problema n-corpi stabilità
Scritto da: Vincenzo Zappalà
Commenti:22
La meccanica celeste diventa veramente celeste **
Facciamo un po’ di chiarezza sull’importanza di una recente scoperta relativa al sistema planetario di 55 Cnc. Sembrerebbe che tutto si riduca ad avere risolto il problema di un’apparente stabilità di due grandi pianeti troppo vicini alla stella e destinati, teoricamente, a scontrarsi tra loro o a essere ingoiati dall’astro centrale. Sicuramente, è sempre bello risolvere un mistero, ma la cosa più importante è, in questo caso, il MODO con cui si è risolto il problema.
Quando si scoprono i pianeti attorno ad altre stelle, i dati in possesso sono piuttosto limitati e si accetta, in prima approssimazione, che ogni pianeta rivolva attorno alla stella seguendo le leggi di Keplero. In altre parole, si considera il problema dei due corpi che ammette sempre una soluzione. Ovviamente, per risolvere il moto è necessario conoscere almeno la massa della stella e la distanza del pianeta, oltre ad avere a disposizione un certo numero di posizioni del pianeta rispetto alla stella. Ed è già un ottimo risultato.
Tuttavia, è solo una base di partenza e non è sicuramente un modello in grado di rappresentare la vera situazione dinamica del sistema. Una celebre stella, 55 Cancri, ha mostrato da diverso tempo di possedere vari pianeti (ciunque) attorno a lei e le osservazioni sono state talmente numerose da rendere finalmente possibile il passaggio da un problema dei due corpi a un problema degli n corpi. Ribadisco ancora che, in questo caso, la soluzione è ottenibile solo attraverso integrazioni numeriche, non avendo il problema una soluzione analitica. E’ la stessa identica cosa che si esegue sui corpi del sistema solare quando si passa a modelli globali. Ciò è stato possibile solo perché il numero di transiti e di altre osservazioni sia spettroscopiche che interferometriche, hanno permesso di avere una mole di dati in qualche modo confrontabile con quelli del sistema solare.
In particolar modo, ci si era accorti che attorno alla stella esistevano due pianeti molto grandi, estremamente vicini e, in seguito, anche una superterra ancora più vicina. Una situazione del genere non poteva essere stabile e quindi i casi erano due: o eravamo stati così fortunati a osservare il sistema in un momento fortunatissimo della sua esistenza oppure vi era un meccanismo di protezione che agiva sui pianeti. Un simile meccanismo poteva essere risolto solo passando al problema degli n corpi, ossia inserendo nei modelli le perturbazioni reciproche dei due giganti, della superterra e dei pianeti più esterni, tra cui un super “Giove” a una distanza circa pari a quella del nostro gigante.
La meccanica celeste è ormai in grado di eseguire calcoli così complicati, sempre che le osservazioni siano in grado di limitare in modo enorme il livello dell’errore ammesso nei calcoli al computer. 55 Cnc è molto fortunata dato che è visibile a occhio nudo e ha anche potuto avere una determinazione diretta del suo raggio. Inoltre, anche solo spostandosi da un osservatorio a un altro, è stato possibile valutare differenze non trascurabili nel moto dei pianeti e quindi informazioni decisive su variazioni orbitali rapide anche se estremamente piccole.
Cosa si è fatto in pratica? Si è imposto che il sistema fosse stabile e si è visto che tipo di interazioni dovevano esserci per ottenere questo risultato. Non è molto diverso dal fatto che nella risonanza 1/1 o 3/2 con Giove vi siano asteroidi stabili (i Troiani e il gruppo di Hilda). Essi sopravvivono solo perché librano attorno a quelle risonanze. Nel caso di 55 Cnc il problema è sicuramente più complesso e non bastano risonanze di moto medio per risolverlo. Tuttavia, si notano altre interazioni che danno luogo ad andamenti periodici coinvolgenti vari parametri orbitali. Nel sistema solare questo tipo di meccanismi protettivi ha permesso di studiare dinamicamente, in modo straordinario, la fascia degli asteroidi e l’evoluzione degli stessi pianeti, fino a tempi di miliardi di anni nel futuro.
Qualcosa del genere si è ottenuto per il sistema legato a una stella che non è il Sole. Il vero interesse della ricerca non è quindi tanto il fatto di avere scoperto che il sistema rimane stabile nel tempo (per almeno 100 milioni di anni), ma soprattutto di aver potuto, per la prima volta, applicare la dinamica degli n corpi a un sistema planetario che non è il nostro e spiegare le interazioni che agiscono. Un passo in avanti enorme, che stimola a ottenere sempre più osservazioni di esopianeti già ben noti, in modo da applicargli modelli a n-corpi come quello utilizzato per 55 Cnc.
Una prima volta è sempre un evento grandioso. Il fatto stesso che il lavoro sarà presentato a un Congresso a Namur, dove lavorano -e hanno lavorato- grandi maestri della meccanica celeste, mi lascia sperare in un qualcosa di rivoluzionario, in grado di aprire una nuova epoca per lo studio dell’evoluzione dinamica di sistemi planetari ben più complicati del nostro.
L’articolo originale (non facile) si trova QUI
Per saperne di più sulla stella 55 Cancri, QUI si parla del suo presunto “pianeta diamante” e QUI dell’atmosfera di quel pianeta
22 commenti
Affascinante, quindi altri sistemi solari potrebbero non per forza sottostare alle leggi di Keplero??? Ma se questi pianeti avessero orbite instabili, prima o poi dovrebbero per forza cedere e tendere all'equilibrio, oppure potrebbero essere ballerini per sempre?
NO, cara Giorgia. le leggi di Keplero vanno bene solo in prima approssimazione anche nel nostro sistema planetario. Se ci fosse solo un pianeta e il Sole, tutto andrebbe bene. Purtroppo non è così e ci sono n corpi che influenzano il moto dei loro amici. Ne segue che le leggi di Keplero sono SEMPRE una prima approssimazione della dinamica planetaria. Il problema è che quando si considerano già solo il Sole, Giove e un altro oggetto le leggi di Keplero non funzionano più e si devono tenere in conto le perturbazioni reciproche tra i pianeti. Purtroppo, il problema dei tre corpi (e a maggior ragione quello degli n corpi) non ha una soluzione analitica e bisogna risolvere la faccenda per mezzo di approssimazioni successive. che oggi, col computer, si possono svolgere in tempi rapidissimi. Per applicare questi metodi è necessario, però, che si conoscano perfettamente tutti i dati fisici e dinamici dei pianeti. Finora ciò era possibile solo per il sistema solare. Ma 55 Cnc ha aperto la strada anche per un altro sistema planetario. OK?
scusa enzo la domanda, ma cosa intendi precisamente dicendo che il sistema non ha una soluzione analitica? intendi dire che non e' possibile fare una previsione precisa a lungo termine?
e quando dici che sono necessarie approssimazioni ai computer cosa si intende? si ipotizza lo stato futuro piu' probabile del sistema e poi ci rifanno i calcoli sopra?
in quel caso li il discorso mi torna perche' piu' avanti nel tempo si va piu aumenta la componente probabilistica e conseguentemente la soluzione diventa solo una ipotesi...
Scusa Enzo,domanda sicuramente sciocca e senza senso, ma con questo calcolo ad n-corpi si può ipotizzare anche l'eventuale esistenza di altri Pianeti non individuati in altro modo?
caro Alex,
intendo proprio dire che il problema dei tre corpi non può essere risolto analiticamente, ossia non è possibile risolvere le sue equazioni come si può invece fare nel caso dei due corpi (orbita kepleriana). Si trovano solo casi particolari, come quelli descritti dai punti lagrangiani. In poche parole, dato un certo numero di osservazioni, anche infinite, non si può trovare una soluzione matematica. Si deve allora andare avanti per iterazioni successive. Ossia si calcolano le orbite come kepleriane per un certo intervallo di tempo. Poi si inseriscono le variazioni previste e si rifanno i conti per un altro dt e via dicendo. Un po' come quando si integra qualcosa di non descrivibile. Se hai una curva di cui non conosci l'equazione, ma solo i punti, puoi sempre considerare la curva come composta da piccoli intervalli lineari. L'intervallo di tempo diminuisce quando vi sono situazioni particolari, come passaggi ravvicinati e cose del genere. Inoltre si può tenere conto solo di Giove o di tutti i pianeti, a seconda di quello che si vuole ottenere e della precisione richiesta. Tutto ciò quando non vi è caos, se no bisogna fare centinaia di simulazioni e scegliere in base a una valutazione statistica. Vi sono, infine, anche processi puramente statistici ma di difficoltà spaventosa... ti assicuro.
Se qualcuno riuscisse a risolvere il problema dei tre corpi, dando una soluzione matematica avrebbe sicuramente una dozzina di Nobel!!!
caro Mario,
in via teorica sì: se quello che hai previsto attraverso i calcoli più raffinati presenta una differenza troppo grande rispetto alle osservazioni, vuol dire che c'è qualcosa da aggiungere. D'altra parte, Nettuno è stato proprio scoperto così. L'integrazione numerica era già nota ai grandi maestri della meccanica celeste, solo che, senza computer, dovevano limitarsi a tempi scala e a precisioni molto basse.
A me l'unica considerazione che viene da fare é che il problema vero che si pone é quello della natura della forza gravitazionale e del suo funzionamento. Evidentemente c'é ancora qualcosa che ci sfugge, altrimenti non penso che saremmo cosí in difficoltá
Alla fin fine la soluzione dei calcoli ci scorre sotto gli occhi, dobbiamo solo riuscire a leggerla
Non credo proprio Andrea... pensa a tutte le perturbazioni che derivano da altri corpi e come possano modificare una traiettoria. Lo stesso corpo perturbato perturba gli altri in modo tale che le loro perturbazioni cambiano di conseguenza e via dicendo, senza alcuna fine. E' come dire che il numero pi greco deve finire e invece assolutamente no. Quando siamo di fronte a equazioni trascendenti e non "finite" c'è poco da fare. la meccanica celeste che lavora solo e soltanto con la gravità e le sue conseguenze è uno dei campi di studio meglio conosciuti e analizzati da secoli. I più grandi scienziati dei secoli scorsi erano arrivati a descrivere strutture a n dimensioni. D'altra parte, se non fosse così, potresti pensare di mandare una navicella nello spazio (con tutte le perturbazioni che ha) e azzeccare il punto e il tempo di arrivo? La gravità potrebbe ancora avere dei segreti, ma non certo nella scala di grandezze del sistema solare. Dovresti leggere qualche testo di meccanica superiore con tutte le equazioni che si tirano fuori e tutte le soluzioni particolari per comprendere che poche cose sono così ben comprese e conosciute. Sembra semplice e invece c'è una infinita varietà di possibilità. E' un po' come la storia del granello di riso sulla scacchiera che diventa due sulla seconda casella e quattro sulla terza. Sembra impossibile, ma non esiste una quantità di grano sufficiente a darti quello contenuto nell'ultima casella. Insomma, a volte le cose impossibili a descrivere possono benissimo far parte della Natura. O, quanto meno, la matematica umana non riesce a descriverle. Ma questo non vuol dire che, allora, bisogna cambiarle. Forse dovremmo cambiare la nostra matematica...
Ok, mi hai ufficialmente incuriosito Enzo
Accetto la sfida! Spero pian piano di acquisire gli strumenti per poter affrontare un testo del tipo che mi hai suggerito
caro Andrea,
preparati... perché sono veramente massacranti!!!! tra Jacobiani e Lagrangiani ci si perde la testa...
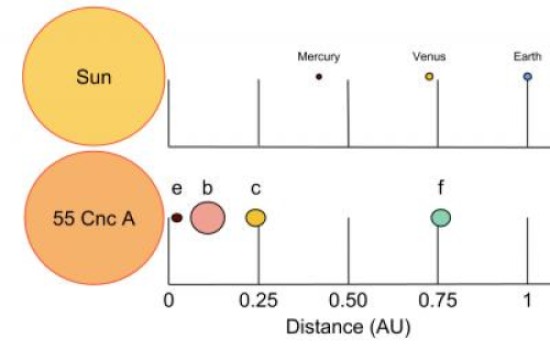
Io, invece, non mi smentisco ed esco dal discorso principale perché è da un po' che mi chiedo una cosa, e l'immagine in alto casca a pennello.
Le distanze di un Pianeta dalla sua Stella o di un Satellite dal suo Pianeta vengono considerate dal centro del corpo principale o dalla sua superficie?
grazie mille per la soiegazione aggiuntiva sulla soluzione analitica, e' stata molto preziosa e avvincente!
per Michael, credo che le distanze per fare i calcoli siano dal baricentro dei corpi anche se dalla figura pare che che sia dalla superficie...
« Inoltre, anche solo spostandosi da un osservatorio a un altro, è stato possibile valutare differenze non trascurabili nel moto dei pianeti e quindi informazioni decisive su variazioni orbitali rapide anche se estremamente piccole. »
Confesso di non aver MINIMAMENTE compreso il significato di questa frase. In che senso lo spostarsi da un osservatorio all'altro ha permesso di valutare differenze? Rammento che per definire il parsec si utilizzava come base trigonometrica il semiasse dell'orbita terrestre, se no non c'era verso di notare differenze di prospettiva dovute alla parallasse... Non mi riesce di vedere cosa possa mutare in senso diagnostico cambiando osservatorio, con distanze a voler essere generosi dell'ordine di sei-ottomila km... quindi non ho capito il punto.
caro Valerio,
mi sono espresso male.... intendevo dire che avendo usato molti telescopi per lo studio delle velocità radiali è stato possibile seguire il movimento e le sue variazioni con precisione estrema.
sulla distanza, Michael ha ragione... Non si dice mai chiaramente come si misurano. Da un punto di vista orbitale sarebbe giusto dare le distanze tra i baricentri dei due corpi o rispetto al baricentro comune. Nel caso di stelle e pianeti di solito si può anche usare la distanza tra i centri delle due sfere. Tuttavia, quando si dice che il Sole dista 8 minuti luce è ovvio che si intende la distanza dalla superficie, quella che emette la luce... ma in realtà si usano valori medi... Nel caso della figura sembra proprio che intendano dalla superficie, ma ... La Terra dista circa 150 milioni di chilometri dal Sole e il raggio del Sole è circa 700 mila chilometri, quindi una certa differenza ci sarebbe, non avvertibile in figura. Comunque sia, nei calcoli dinamici ti assicuro che usano le distanze dal baricentro del sistema....
Ammetto, ci vorrebbe maggior chiarezza...
Quindi il disegno del Sistema 55 Cnc non è in scala? Se così fosse, i primi tre Pianeti dovrebbero essere all'interno del loro Sole...
No, Michael! E' in scala solo per le distanze, ma non certo per le dimensioni tra pianeti e stella...
Ecco, appunto. ;) Grazie.
"Lo stesso corpo perturbato perturba gli altri in modo tale che le loro perturbazioni cambiano di conseguenza e via dicendo, senza alcuna fine".
ma questo si potrebbe già considerare come caos?
No Davide... non è caos, perché è qualcosa di determinabile anche se estremamente complesso. Al limite sai fino a che punto potrai ottenere una certa precisione. Il caos nasce quando una variazione infinitesima non deducibile dalla fisica del fenomeno porta a soluzioni completamente diverse (un cambiamento nell'ultimo decimale, cambiare computer,...)
grazie enzo,volevo chiedere un'altra cosa; riporto una tua risposta da un' altra discussione:
"la forza di gravità non ha limiti di distanza e quindi, teoricamente, se non ci fosse nessun altro oggetto nell'universo tranne due stelle, queste potrebbero orbitare attorno al proprio baricentro anche a distanza praticamente infinita. ne segue che ciò che limita l'interazione gravitazionale è la presenza degli altri oggetti e sistemi "
un sistema,quindi, è confinato a se stesso; se prendiamo ad esempio il sistema solare nel suo complesso (dal sole a tutta la nube di oort),questa "bolla" risente gravitazionalmente delle bolle confinanti? se per casi chessò ,di moto proprio, il sistema alfa centauri si avvicinasse a noi ben più di ora potrebbe influenzare i nostri meccanismi interni o il sistema solare "reagirebbe" nel suo complesso,mantenendoli inalterati? se si potesse stilare una sorta di "mappa" gravitazionale nello spazio interstellare,ci sarebbero confini di stato ben precisi?zone franche? spero di essermi spiegato
Bravissimo Davide,
. La gravità non ha limiti, ma possiamo considerare che fino a una certa distanza da una massa M giochi solo quella esercitata da quella massa. Una approssimazione, che funziona benissimo se ci si limita a studiare i fenomeni locali. Se, come dici tu, Alpha Centauri si avvicinasse troppo, dovremmo tener conto anche del suo campo gravitazionale (paragonabile a quello del Sole) e i moti planetari e quelli delle stesse due stelle dovrebbero cambiare. E' questo il caso delle comete della nube di Oort che sono legate (leggermente, data la distanza dal Sole) alla nostra stella, ma che risentono subito del passaggio relativamente distante di una stella vicina. Subiscono una variazione del moto e finiscono su orbite che possono portarle verso il Sole.
ti sei risposto da solo
In generale, se tenessimo conto di tutte le masse dell'universo, avremmo un intricato sistema gravitazionale a cui partecipano tutti gli oggetti. Proprio questo sistema è quello che cerca di controbattere l'espansione dello spazio. La forma dell'universo dipende proprio da come agisce un qualsiasi corpo soggetto alla gravità globale... e quindi cadiamo nella curvatura... Tutto è collegato nell'Universo.
Gli articoli che sto scrivendo sulla forza centrifuga (solo uno spunto, però) aiuteranno molto nel capire come si reagisce a un campo gravitazionale e può portarci al caso delle stelle doppie, dei punti lagrangiani e poi ancora agli ammassi globulari, agli ammassi aperti, agli ammassi di galassie e, infine, alla struttura a grande scala dell'Universo.
Bene, bene, sei proprio sulla strada giusta! Vedrai che ti piaceranno molto!!!
PS: sto lavorando duro, perché ogni cosa che scrivo mi spinge a un passetto più in là ed è difficile non scrivere un libro completo di fisica elementare... Insomma, pensavo di cavarmela con due articoli, ma sono già al terzo e so di dovere scrivere almeno il quarto...