Prima di iniziare, fatemi riassumere un concetto di massima che mi sembra non completamente digerito, normalmente: l’inerzia di un corpo. Abbiamo detto che possiamo considerare la massa come il segno più indicativo di questa caratteristica di ogni oggetto celeste (e non solo), ma il concetto ha una valenza estremamente generale e fondamentale. La richiamo ancora: ogni corpo tende a muoversi di moto rettilineo uniforme se nessun disturbo esterno lo viene a perturbare. In altre parole: ogni corpo cerca in tutti i modi di mantenere questo stato di PIGRIZIA, ossia di inerzia. Qualsiasi cosa si cerchi di fare a un corpo, vuol dire lottare contro la sua inerzia. Anche se alla fine cede e si adegua, la sua inerzia deve entrare in gioco. Non dimentichiamolo mai!

Una sfida all’ultimo sangue

Stavamo cercando il mandante del sicario accelerazione, l’unico capace di variare quella velocità costante che permetterebbe al corpo di accontentare la sua inerzia. Non è difficile risalire al mandante, una volta che conosciamo il sicario (almeno nella fisica). Basta fare uscire allo scoperto i due contendenti principali: la massa del corpo (l’inerzia) che tende a ribellarsi ai disturbi esterni e il mandante che cerca, invece, di andare contro la pigrizia del corpo. E’ una specie di braccio di ferro o di duello da Far West. La massa affronta il mandante e il duello ha inizio. Purtroppo, sappiamo già chi è il vincitore, dato che quasi tutti i corpi celesti non sono in moto rettilineo uniforme. Il mandante vince sempre, ma la massa riesce a limitare i danni. Una vittoria più o meno eclatante che dipende da quanto sia resistente la massa. Non è difficile avere un’idea della sfida: basta fare il rapporto tra mandante e massa. Fatemi chiamare il mandante forza e indicarlo con F. La sfida si può rappresentare quindi come:

F/m

A cosa è uguale questo rapporto (occhio che F è un vettore, dato che ha modulo, direzione e verso così come il suo sicario)? Beh, deve essere qualcosa che indichi chiaramente quanto la vittoria della forza sia netta e decisiva. Vi faccio un esempio banalissimo che ci tornerà presto utile. La Terra, intesa come pianeta, cerca di disturbare il Sole e fargli cambiare velocità (che possiamo immaginare, in prima approssimazione, come uniforme e diretta sempre lungo una retta). Lo scontro è tra la forza che la Terra esercita sul Sole e la massa del Sole. Anche in questo caso, la vittoria della Terra é sicura (come al solito), ma le costa molto cara e, praticamente, nessuno se ne accorge. Se invece io lascio libero un bicchiere  davanti a me, la battaglia avviene tra la forza esercitata dalla Terra sul bicchiere e la massa del bicchiere. Sapete tutti la conclusione di una sfida davvero impari. La vittoria è così netta che il bicchiere va in mille pezzi sul pavimento. Ci torneremo presto…

Il rapporto potrebbe quindi essere qualcosa di estremamente piccolo, ma anche di estremamente grande. Un lieve schiaffetto o un pugno massacrante. Che cosa esce fuori dallo scontro all’ultimo sangue? Beh… solo e soltanto il sicario che ha via libera di agire sulla povera velocità. La massa ha fatto il possibile, limitando i danni, ma poi deve accettare la sconfitta con grande cavalleria e umiltà. Ha vinto il più forte e il sicario è libero di andare a compiere la sua azione. La “violenza” del sicario è proprio ciò che esce fuori dalla sfida. Possiamo, perciò scrivere:

F/m = a

Potremmo anche scriverla così:

m = F/a

Il significato sarebbe: la massa indica quanto la forza del mandante è costretta a ridurre l’azione che il suo sicario può compiere sulla vittima. Più la massa è grande, più piccola è l’azione del sicario accelerazione, a parità di mandante. Potremmo anche dare un’altra definizione: se il mandante aumenta la propria forza verso un corpo di massa m, la sua accelerazione deve aumentare ma solo in modo che il loro rapporto, ossia la massa m, rimanga costante. In altre parole, per permettere al sicario accelerazione di aumentare la sua violenza sulla vittima deve anche aumentare la forza che comanda il sicario. La massa regola questo rapporto che non può cambiare, dato che essa è sempre la stessa, per un certo corpo.

Il secondo principio della dinamica

Potremmo scrivere un libro sul modo di interpretare il secondo principio della dinamica. Basta, però, con gli scherzi e scriviamo il principio nella sua forma più nota:

F = ma

Essa ci dice che l’accelerazione che agisce su un corpo è direttamente proporzionale alla forza che l’ha generata ed è inversamente proporzionale alla massa del corpo. Ben poco da aggiungere: Newton era proprio un GENIO, oltre che un detective fantastico. E’ riuscito con una banale formuletta a legare sicario e mandante, solo conoscendo l’inerzia della vittima.

Una vendetta cosmica

Non ci rimane che introdurre anche il terzo principio della dinamica, ossia il principio della … vendetta. Passatemi questa parola anche se siamo in un ambiente che non segue le squallide reazioni umane. State bene attenti al suo enunciato, perché può causare, a volte, confusione o false interpretazioni. Ecco, perché ho usato la parola “vendetta”. Se un corpo A agisce su un altro corpo B attraverso una forza F, il corpo B reagisce agendo sul corpo A con una forza uguale e contraria. Molta attenzione a chi agisce e dove agisce. Se un corpo A agisce su B, il corpo B deve agire su A. La forza è uguale e contraria, ma chi la subisce non è lo stesso corpo. Questa precisazione sarà utilissima nello spiegare la forza centrifuga.

Bene, abbiamo concluso la nostra … premessa. Se andavo avanti così avrei descritto tutta la meccanica classica. Meglio che mi fermi e torni alla Luna.

Sezioniamo il sicario

Tuttavia, non mi sento ancora tranquillo e in pace con me stesso. Avevo promesso di utilizzare le derivate per risolvere il problema dell’accelerazione. Sarebbe comodo girarci intorno come avevo fatto nella Fisica addormentata nel Bosco. Però, una promessa è una promessa. Allora, facciamo così: utilizzerò entrambi i metodi, quello più avanzato e professionale e quello approssimato e -forse- più intuitivo. In qualche modo, tutti avranno in mano la soluzione.

Riassumiamo, ancora una volta, la situazione a cui siamo arrivati. Un corpo celeste tende a mantenere per sempre il suo stato di moto rettilineo e uniforme. Se non vi riesce, qualsiasi sua azione appare identica se osservata da un qualsiasi sistema inerziale, ossia che si muova rispetto a un collega di moto rettilineo e uniforme. Ricordiamo che il moto inerziale si verifica SEMPRE quando non esiste nessun mandante (forza) e sicario (accelerazione) che agisce sul corpo.

Appena subentra questa situazione di disturbo, la massa (ossia l’inerzia del corpo a mantenere il suo moto rettilineo e uniforme) sfida a singolar tenzone la forza (il mandante) in modo da limitare l’azione violenta operata dal sicario (accelerazione). Tuttavia, la massa può solo limitare i danni ed è costretta ad accettare il cambiamento della situazione. Il modo più sicuro per capire se un corpo ha subito l’azione di un mandante è la variazione della sua velocità e, in particolare, della sua traiettoria. Se capita quest’ultima situazione siamo certi che sta agendo un’accelerazione. Se il moto continua a essere rettilineo bisogna controllare se la velocità aumenta o diminuisce il proprio modulo. Nel caso di una traiettoria curva abbiamo sicuramente un’accelerazione centripeta, normale alla tangente alla traiettoria nel punto P; nel caso che il moto resti rettilineo, ma non uniforme, abbiamo soltanto un’accelerazione tangenziale. Il caso più generale è ovviamente quello in cui cambia sia il modulo che la direzione della velocità, per effetto del sicario accelerazione.

Data un certa traiettoria curvilinea e una certa velocità, vogliamo calcolare l’accelerazione che subisce il corpo nel punto P. Abbiamo già descritto la situazione, ma adesso vogliamo eseguire il calcolo matematico. Vi sono due modi. Uno che sfrutta le derivate e uno che, sebbene approssimato, conduce allo stesso risultato. Li descrivo tutti e due, ricordando che il secondo è quello descritto nella Fisica addormentata nel Bosco. Chi non se la sente può saltare la parte che segue fino al prossimo paragrafo.

Facciamo un ulteriore passo avanti. Abbiamo visto che un vettore ha dentro di sé tre caratteristiche: il modulo, la direzione e il verso. In particolare, il modulo è un numero, vincolato, però, al vettore. Ne consegue che scrivere v è cosa diversa  dallo scrivere v. Su v posso eseguire calcoli matematici semplici, su v è più complicato.

Posso, però, utilizzare un piccolo trucco. Introdurre un vettore unitario, ossia un vettore che abbia modulo unitario (in relazione all’unità di misura usata) e moltiplicarlo per il modulo. Questo vettore unitario lo chiamo versore. Ho creato una specie di “chiocciola” che si porta dietro un “guscio”. La chiocciola è il versore che può girare e cambiare verso, il modulo è il guscio che viene trascinato senza poter agire direttamente. Chiamiamo u il versore. Posso allora scrivere che la velocità v è data da:

v = vu

Sono riuscito a separare il modulo dal versore, in modo da poterli trattare separatamente. Tuttavia, la velocità (o un vettore, in generale) non perde la sua identità.

Consideriamo la Fig. 4, in cui abbiamo una traiettoria curvilinea qualsiasi. Ovviamente, guardiamo la situazione da un sistema di riferimento inerziale, ossia tale che potrei sempre cambiarlo spostandolo di moto rettilineo uniforme. Un sistema, in particolare, che NON SUBISCE accelerazioni di sorta da nessun mandante inopportuno. Ciò che subisce il corpo P è visto nello stesso modo in uno qualsiasi di questi sistemi. Ricordiamolo sempre, mi raccomando!

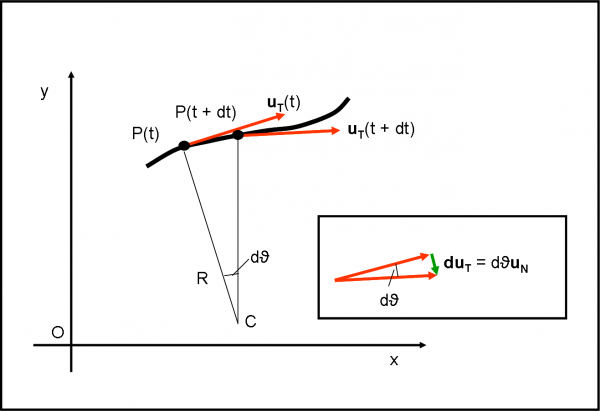
Il punto P(t) si sposta in P(t + dt) di una quantità piccolissima che, misurata sulla curva, è uguale a un certo ds. Ciò lo fa in un intervallo di tempo dt. Un ds talmente piccolo che può essere approssimato perfettamente dal cerchio osculatore in P alla curva. Ne segue che la distanza tra P(t) e P(t + dt) dal centro istantaneo C del cerchio osculatore è sempre uguale a R. Visto dal centro C il trattino ds, corrisponde a una variazione piccolissima dell’angolo ϑ. Posso scrivere tranquillamente che:

ds = R dϑ    …. (1)

Adesso disegniamo qualche vettore. Iniziamo con le velocità in P(t) e P(t+dt). Consideriamo solo il loro versore, dato che per adesso c’interessa solo la variazione di direzione. Il versore velocità in P(t) lo chiamiamo u_T(t) e quello in P(t + dt), u_T(t + dt). Sono, ovviamente entrambi funzione del tempo, hanno lo stesso modulo unitario, mentre l’indice T indica solo che essi devono essere diretti lungo la tangente alla curva. L’angolo dϑ, definito prima, è esattamente lo stesso formato tra le direzioni di u_T(t) e u_T(t + dt), dato che sono entrambe perpendicolari al raggio R.

Definito u_T posso immediatamente definire u_N, ossia il versore diretto verso il centro C che deve essere, per definizione, perpendicolare a u_T. Nel quadratino a destra eseguo la solita differenza di vettori, anzi di versori. I due versori che considero non sono altro che quelli relativi alle due velocità in P(t) e P(t + dt), che, come detto, formano tra di loro un angolo dϑ. Posso quindi scrivere senza problemi che (ricordando la (1)):

du_T= (dϑ ·1)u_N     (il modulo del versore u_T è uguale a 1)

Dovremmo avere tutti i dati per passare alla vera velocità e all’accelerazione che è stata in grado di trasformarla da quella che era in P(t) a quella che è adesso in P(t + dt). Come avete visto, finora non abbiamo parlato di moduli, ma abbiamo solo lavorato con versori, ossia solo con direzione e verso delle velocità.  Torniamo, quindi alla relazione:

v = v u_T   …. (2)

Ho scritto u_T perché so di sicuro che la velocità deve avere la direzione del versore tangente. Che cos’è l’accelerazione? Ormai lo sappiamo bene: essa si calcola facendo la derivata della velocità rispetto al tempo. Non ci resta, allora che fare la derivata della (2) rispetto al tempo. Compaiono dei vettori e degli scalari? Poco importa, basta ricordarsi che la derivata di un vettore rimane un vettore così come la derivata di uno scalare rimane uno scalare. Dopo tanta fatica, ecco che finalmente capite perché ho aspettato di descrivere la derivata di un prodotto. Infatti, devo eseguire:

a = dv/dt = d(v u_T)dt

Ossia scrivere la derivata di un prodotto (v u_T). Ormai sappiamo come fare:

a = d(v u_T)/dt = (dv/dt) u_T + v (du_T/dt)    …. (3)

(ricordate? y’ =  f ’(x)g(x) + f(x) g’(x)).

Avete sicuramente notato che la velocità v compare solo come modulo. Alla direzione e al verso ci pensa il versore.

La relazione di prima può essere elaborata, dopo tutto il lavoro che abbiamo svolto poco fa.

Abbiamo, infatti trovato che:

du_T= dϑ u_N  

e quindi anche:

du_T/dt= (dϑ/dt) u_N

Sostituendo nella (3):

a = (dv/dt) u_T + v (dϑ/dt) u_N

Avevamo, però, anche ricavato che:

ds = R dϑ,   ossia:    dϑ = ds/R

Sostituisco ancora e ottengo:

a = (dv/dt) u_T + (v/R)(ds/dt) u_N

Cos'è, però, ds/dt ? Lo sappiamo bene, fin dalla volta scorsa: non è altri che la velocità (in modulo). Infatti: v = ds/dt.

Ultima sostituzione e otteniamo infine la relazione fondamentale e generale per l’accelerazione agente su un corpo che si muove di moto curvilineo qualsiasi:

a = (dv/dt) u_T + (v²/R) u_N

Essa ci dice proprio che l’accelerazione si può scomporre lungo due direzioni perpendicolari tra di loro (tangenziale e normale o centripeta). La componente lungo la tangente (indicata dal versore u_T) ha modulo dv/dt, ossia proprio la variazione del modulo della velocità (possiamo chiamarla accelerazione tangenziale). Questo vuol dire che se la velocità non cambia in modulo passando da P(t) a P(t + dt), questo termine va a ZERO. In altre parole, non esiste accelerazione tangenziale.

La componente lungo la direzione normale alla tangente, ossia verso il centro del cerchio osculatore istantaneo, ha un modulo estremamente importante che vale v²/R. Esso indica l’intensità, dell’accelerazione centripeta. Se il moto è curvilineo questa componente esiste sempre. Ossia, come già detto precedentemente, un moto curvilineo ci assicura che esiste un’accelerazione normale alla tangente alla traiettoria.

Due precisazioni. Abbiamo usato la scrittura dy/dx per indicare la derivata. In questo modo l’abbiamo sempre indicata come un rapporto tra grandezze infinitesime. Il solo scrivere dy/dx, però, non indica solo un rapporto tra segmenti o tratti di curva o di tempo piccolissimi, ma indica già che  queste grandezze stanno tendendo a zero, ossia proprio il concetto di derivata. Tuttavia, la scrittura permette anche di sostituire, ai singoli intervalli piccolissimi, valori corrispondenti in cui appaiano altre grandezze.  Al posto di dϑ abbiamo potuto, ad esempio, scrivere ds/R. Un grande aiuto nel calcolo, pur non variando assolutamente il concetto e il risultato della derivata. In parole matematiche lo scrivere:

a(t) = dv/dt

significa:

a(t) = lim _dt→0 (v(t + dt) – v(t))/dt

La seconda precisazione è un po’ più complessa. Nel calcolo precedente abbiamo fatto la derivata di un versore, ossia di un qualcosa che ha sempre modulo costante e unitario. Alla fine abbiamo trovato che (a parte le costanti numeriche che l’hanno moltiplicato) si è trasformato in un versore normale a quello di partenza. Questo fatto ci permette di concludere che la derivata di un versore è un versore perpendicolare al primo. Potremmo parlare per ore di versori e dimostrare questa conclusione in altri modi, ma direi di non esagerare… non vorrei che la forza centrifuga resti un sogno irraggiungibile.

Aggirare un ostacolo non è sempre dignitoso, ma a volte semplifica la vita

Ammetto che le derivate di vettori non sono un esercizio molto facile, anche perché bisognerebbe prendere dimestichezza con i versori e con le componenti lungo di essi del modulo. Vi ripropongo, allora, il metodo usato nel libro, anche perché a noi, in fondo, interessa solo il valore finale della accelerazione centripeta. Fate, però attenzione che è valido solo nel caso che il modulo della velocità non vari col tempo.

Consideriamo la Fig. 5, in cui il modulo della velocità resta costante (varia solo la direzione). Il triangolo isoscele PP’C è simile al triangolo formato dalle due velocità in P e P’. La differenza delle velocità e data da dv.

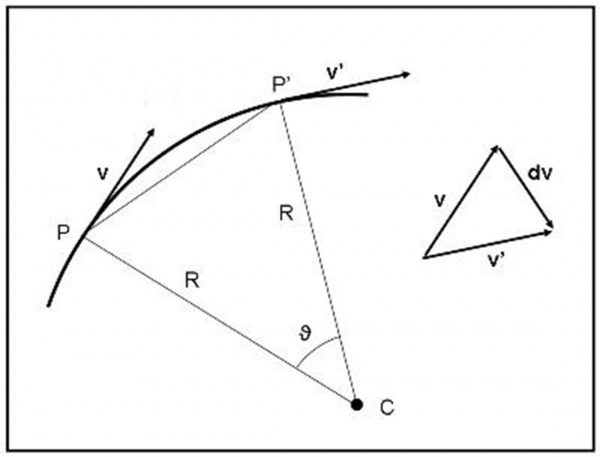
Dai triangoli simili posso scrivere (in modulo):

dv/v = PP’/R

A questo punto possiamo assumere, in prima approssimazione, che PP’ diviso per dt tenda al modulo della velocità v.  Ossia:

PP’ = v dt

E quindi:

dv/v = v dt/R

Attenzione: dv è il modulo della differenza di velocità e non la differenza dei moduli che sarebbe uguale a 0, per definizione di velocità a modulo costante. E’ immediato che:

dv = v² dt/R

Ma dv/dt è il modulo dell’accelerazione centripeta e, concludendo, si ha che:

a_C= v²/R

Il risultato è lo stesso ottenuto precedentemente. Non abbiamo usato vettori e versori, ma solo moduli, ossia scalari. Tuttavia, si sono fatte approssimazioni che diventano trascurabili solo se si fanno tendere a zero certe quantità, il che ci porta nuovamente al concetto di derivata. Teniamo anche presente che questa modo di agire è valido solo se la velocità ha modulo costante.

Dato che è proprio questo il caso che c’interessa, l’importante è che, in un modo o nell’altro, siamo stati capaci di ricavare l’accelerazione centripeta in un punto P.

La determinazione dell’accelerazione centripeta ci permette di entrare, finalmente, nell’argomento che volevamo trattare, ossia nel moto circolare uniforme, proprio quello che ci aiuta a capire se la Luna cade oppure no. Vi invito già a pensare a quello che sarà il problema fondamentale legato alla forza centrifuga. Un moto circolare uniforme non è un moto rettilineo uniforme. Se uso un sistema di riferimento inerziale, la descrizione del fenomeno deve essere diversa rispetto alla descrizione fatta in un sistema di riferimento che segue il moto circolare. Questo è un obbligo per far sì che il fenomeno fisico resti identico.

Direi che l’ho fatta lunga… mi dispiace, ma dovrete aspettare ancora un po’ per toccare con mano la forza centrifuga. Ho preferito, però, essere, come al solito, lungo e ripetitivo per cercare di farvi arrivare al nocciolo della questione in condizioni ottimali. Tra parentesi, vi assicuro che non vi sarà più bisogno di derivate….