Una simpatica filastrocca di Sergio Endrigo ci aiuta ad affrontare di petto le quattro dimensioni. Non solo parlandone e cercando di spiegarne il significato e le ripercussioni, ma proprio provando a DISEGNARE in quattro dimensioni. Lo faremo in due modi: uno come conseguenza degli articoli sull’aberrazione relativistica, dove le quattro dimensioni saranno espresse in un disegno che permette di leggerle contemporaneamente, anche se in modo simbolico; l’altro come puro e semplice esercizio di matematica e geometria. Cominciamo da quest’ultimo. Ragazzi… che faticaccia… spero sia comprensibile e interessante!

Oltre alla canzoncina del titolo, vi sono almeno due libri che possono servire molto per la comprensione di questo articolo (sia se letti prima o dopo). Uno è il celebre Flatlandia di Edwin Abbott del 1884, l’altro è un divertente racconto di fantascienza di quel geniale autore che è Robert Heinlein, La Casa Nuova. Lo scopo di entrambi è di arrivare a descrivere, in modo romanzesco, una figura a quattro dimensioni.

Andiamo avanti in parallelo tra matematica e rappresentazione grafica. Vedremo che la prima ci porta a un risultato positivo senza alcun problema concettuale, mentre la seconda ha bisogno di molta fantasia e immaginazione. D’altra parte, ricordiamo che la matematica non ha alcun problema a entrare in mondi inaccessibili alle nostre caratteristiche fisiche, mentre il disegno è vincolato alle due dimensioni del foglio o, al limite, alle tre della scultura, ma non può certo permetterci di entrare nella quarta. Un confronto impari che abbiamo già studiato all’inizio del nostro piccolo corso di matematica.

La matematica non ha problemi a definire concetti come zero, infinito e cose del genere. La fisica e la geometria si trovano, invece, di fronte a ostacoli insormontabili. Prendiamo l’esempio del punto all’infinito. La matematica lavora tranquillamente nel piano ampliato, mentre la geometria ha bisogno di un artificio prospettico: le due rotaie che sembrano incontrarsi guardando sempre più lontano. La fisica ci dive che non è vero, ma l’escamotage grafico rende molto bene un concetto che la matematica non ha problemi ad affrontare compiutamente. Per potere disegnare un oggetto a quattro dimensioni dovremo quindi usare artifici prospettici e proiettivi che daranno solo una rappresentazione parziale di ciò che la matematica definisce con una semplicità quasi irrisoria.

Per non complicare troppo le cose, consideriamo una delle figure più semplici e simmetriche della geometria a tre dimensioni: il cubo. Si potrebbe fare con qualsiasi altra sua “sorella” ma ci complicheremmo inutilmente la vita. Accontentiamoci del caro e vecchio cubo.

Come sempre capita nello spazio, iniziamo con il punto, un nostro vecchio amico, che pone la fisica di fronte a un limite insuperabile: le dimensioni nulle. La matematica non ha titubanze e lo definisce tranquillamente. Bene, il nostro primo cubo lo chiamiamo 0-cubo, ossia una figura (qualsiasi e quindi anche un cubo) in uno spazio a zero dimensioni. Non abbiamo bisogno di nessuna figura, dato che il punto non ha né altezza, né lunghezza e nemmeno lunghezza. Il punto rappresenta il niente, non ha dimensioni e quindi ha zero lati, zero facce, zero spigoli, zero volume, zero superficie e via dicendo… Niente di “speciale”, ma necessario per sapere da dove iniziare il nostro viaggio verso le n dimensioni.

Il primo salto quantitativo è disegnare il cubo a una dimensione, ossia l’1-cubo. Tutto lo spazio sta, per definizione, su una linea che possiamo tranquillamente considerare una retta (quante volte l’abbiamo fatto per descrivere l’espansione dell’Universo…). Cosa si deve fare? Prendere un punto P sulla retta e spostarlo di una certa quantità L. Otteniamo un altro punto P’. Il segmento tra i due punti può essere definito come il cubo di dimensione uno. In realtà, dovendo stare su una retta, non possiamo certo fare di più. Comunque, possiamo già concludere che l’1-cubo è delimitato da due punti e ha una lunghezza (l’unica dimensione che abbiamo a disposizione) L. Le “cose” geometriche che delimitano lo spazio considerato le chiamiamo facce F, mentre lo spazio compreso tra di loro lo chiamiamo volume V. Ossia V = L.

Attenzione: ho assegnato dei nomi che conosciamo bene per il loro significato molto più particolare, ma facciamo questo sforzo che si dimostrerà molto utile tra non molto.

Disegniamo quanto detto a parole nella Fig.1(a). Vi è lo spazio-retta (1-dimensione), i due punti P e P’ (le due facce) e la lunghezza L (il volume). L’1-cubo è proprio PP’, punti compresi.

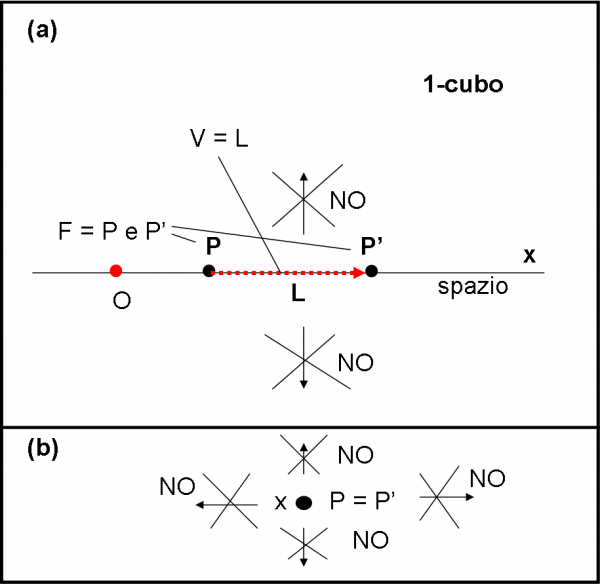
Attenzione di nuovo: abbiamo disegnato lo spazio-retta su un piano, ma questa è una visione che usiamo noi che abbiamo la fortuna di vivere in un mondo a tre dimensioni e di disegnare su un piano a due dimensioni. Tra non molto, questa fortuna sparirà. Non illudiamoci più di tanto.

E’ cosa saggia, per prepararci a ciò che succederà tra poco, immedesimarci in un abitante dello spazio a 1-dimensione (ossia in chi vive sulla retta x). Cosa vedremmo? Solo un punto sia davanti che dietro. Come potremmo rappresentare il nostro 1-cubo in un disegno, se fossimo in O? Niente da fare, solo con una delle sue due facce P e/o P’, a seconda di dove ci troviamo. Potendo muoverci, però, passeremmo da P a P’ e, usando il cervello e il tatto, potremmo calcolare il nostro movimento e dire che abbiamo percorso un tratto PP’, ossia ci renderemmo conto dell’esistenza dell’1-cubo e di come è fatto. Ricapitolando, vivendo in una dimensione, riusciamo a vedere in zero dimensioni, ma a intuire e calcolare un 1-cubo. Ciò che vede l’abitante O, dello spazio a una dimensione, è rappresentato nella Fig. 1(b). Gli spostamenti verso destra, sinistra, sopra e sotto, sono, ovviamente, vietati! Non commettiamo, subito, un errore fondamentale. Per poter descrivere l’1-cubo sotto vari punti di vista bisognerebbe poter girare attorno a lui, ossia muoversi in due dimensioni e noi non possiamo farlo.

Facciamo il passo successivo e costruiamo lo spazio a due dimensioni (ad esempio un piano). Basta aggiungere anche l’asse y e avere il nostro ben noto sistema cartesiano. Cosa avevamo fatto per passare da uno 0-cubo a un 1-cubo? Avevamo fatto muovere il punto P, lungo il suo unico mondo, di una lunghezza L.

Non ci resta che fare la stessa identica cosa sfruttando la seconda dimensione (l’asse y) nella Fig. 2(a). Prendiamo il nostro 1-cubo (il segmento PP’) e spostiamolo lungo la direzione y (la nuova dimensione). Lo spostiamo di una lunghezza pari a L. Uniamo gli estremi corrispondenti dei due segmenti e otteniamo il cubo a due dimensioni, ossia il 2-cubo. Lo conosciamo bene e lo chiamiamo, di solito, quadrato.

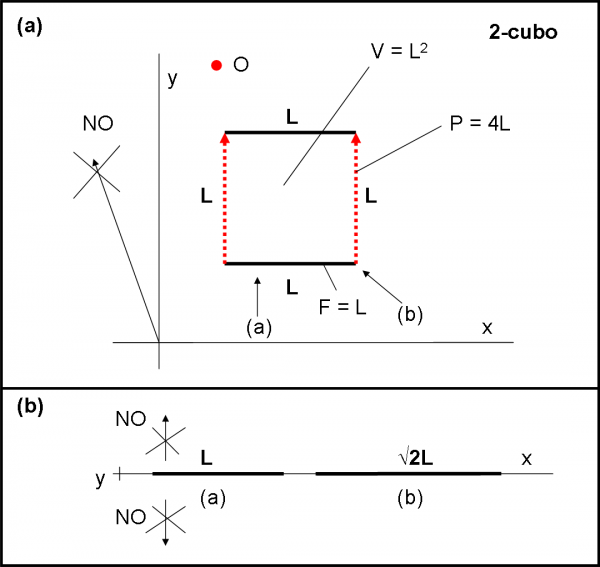
Cosa è successo matematicamente? Una lunghezza L si è trasformata in 4 lunghezze L. Le facce F, che prima erano i due punti P e P’, sono adesso i quattro lati del quadrato. Le quattro facce delimitano una parte di spazio, ossia un volume V = L², ossia L volte la lunghezza L.  Riassumiamo il tutto in modo un po’ più rigoroso e matematico:

1-cubo:  due facce (P e P’) e un volume L, delimitato dalle due facce.

2-cubo:  quattro facce (PP’, PQ, QQ’, Q’P’), un volume V = L² , delimitato dalle quattro facce.

Possiamo già scrivere una formula semplice semplice che schematizza il passaggio da una a due dimensioni. Per costruire il quadrato abbiamo avuto bisogno di spostare un lato PP’ fino a QQ’. Ossia siamo partiti da due facce di partenza (due segmenti). Per avere il numero totale di facce (lati) non abbiamo fatto altro che eseguire la banale moltiplicazione:

2 facce x 2 dimensioni = 4 facce

Questa relazione valeva anche nel passaggio da zero a una dimensione? Beh avevamo un punto P e lo spostavamo in P’. Le facce di partenza (punti) erano 2 e le dimensioni 1. Si può anche scrivere:

2 facce  x 1 dimensione = 2 facce

Insomma, potremmo anche pensare che per conoscere il numero totale di facce che delimitano l’n-cubo basta moltiplicare il numero di facce di partenza (sempre e comunque due: due punti, due lati, ecc.) per il numero delle dimensioni. In poche parole, il numero di facce è sempre il doppio del numero delle dimensioni. Vedremo se continua a funzionare…

Anche la Fig. 2(a) è tipica di un osservatore fortunato. Stiamo, infatti, guardando uno spazio a due dimensioni “dall’alto”, ossia utilizzando una terza dimensione. Immergiamoci, nuovamente, nel mondo a due dimensioni, il piano xy. Cosa vedremmo? Solo e soltanto segmenti, ossia figure a una dimensione. Un osservatore O che guarda il 2-cubo, lo vede come segmento. L’unico vantaggio che ha, rispetto allo spazio precedente, è che un quadrato visto da varie angolazioni cambia la sua lunghezza. Può andare da una minima uguale a L, fino a una massima pari alla diagonale del quadrato, ossia √2 L (teorema di Pitagora), come mostrato nella Fig. 2(b).

Chi vive nello spazio a due dimensioni non può vedere la forma del quadrato. La può però intuire proprio dalla variazione della lunghezza del segmento. Infatti, questa volta, gli è permesso di muoversi nel piano xy. Con il cervello e il tatto (ma anche con l’ombra se esiste un Sole), può, allora, anche calcolare qualcosa che può chiamare “area”, un qualcosa che è contenuta all’interno dei quattro lati (facce), ossia il volume V. Basta che segua una faccia (un segmento), poi si giri di novanta gradi e vada avanti per un altro tratto L, nuova deviazione di 90° e così via fino a tornare la punto di partenza. Sì, può costruirlo, ma non vederlo direttamente. Lui vive nelle due dimensioni, può intuirle entrambe, tracciare un percorso, ma vederne solo una. Ovviamente, non può spostarsi sopra o sotto il piano xy.

Siamo pronti ad aggiungere un’altra dimensione, la terza? Sembrerebbe di sì: non ci resta che inserire l’asse z. La matematica sta scalpitando… ma la geometria e la vista ci impongono qualche riflessione.

Noi aggiungiamo l’asse z nel piano del foglio, ossia in uno spazio a due dimensioni! La nostra vista, infatti, lavora essenzialmente su due dimensioni. Solo il cervello, il calcolo e/o la manipolazione ci permettono di capire e stabilire la terza. Siamo nelle stesse condizioni del quadrato di prima. Anche chi vive nel piano del foglio, può immaginarsi un quadrato girandogli attorno e costruirlo attraverso il calcolo e la “manipolazione”, ma non può mai vederlo. Così capita a noi se guardiamo una figura a tre dimensioni. Solo la mente, la visione stereoscopica, le ombre, il tatto, riescono a farci capire che esiste la terza.

Il procedimento è, comunque, sempre lo stesso. Prendiamo un quadrato (2-cubo) e lo spostiamo di una certa lunghezza L lungo la terza dimensione (Fig. 3). Fermiamoci subito…

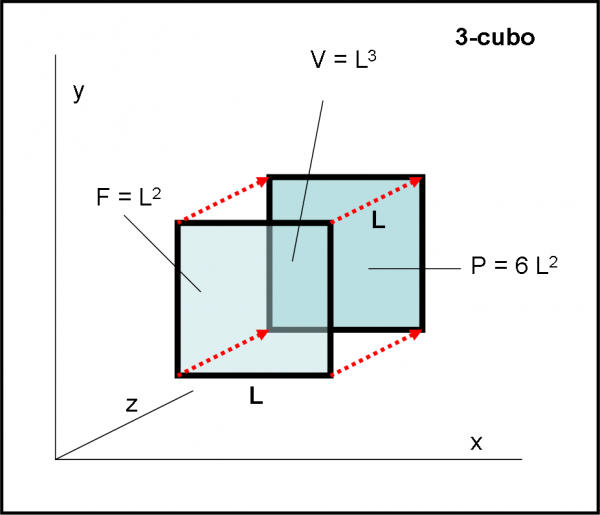
Questa volta non posso vedere la figura “dall’alto”, ossia dalla dimensione superiore, come fatto finora. Dovendo disegnare su due dimensioni, devo utilizzare procedimenti grafici come la prospettiva o l’assonometria. Ossia, qualcosa che simuli la terza dimensione su un foglio a due dimensioni. Il risultato è, quasi sempre, interpretabile facilmente, dato che noi siamo abituati a vivere e a costruire nelle tre dimensioni. Questa limitazione è spesso trascurata, ma va tenuta bene in conto. Solo il fatto di vivere in uno spazio a tre dimensioni ci permette di comprendere una sua proiezione nelle due dimensioni. Nello stesso identico modo in cui un abitante dello spazio a due dimensioni può disegnare solo nella dimensione singola e interpretare e riconoscere una figura a due dimensioni attraverso accorgimenti speciali (colori diversi per ogni lato, ombreggiature,…). Tuttavia, ricordiamo ancora che chi vive nelle due dimensioni sa costruire nelle due, così come chi vive nelle tre sa costruire nelle tre (una scultura, qualsiasi manufatto, ecc., ecc.).

Un piccolo commento “artistico”. Come ormai abbiamo compreso molto bene, l’uomo costruisce in tre dimensioni, ma disegna (ed essenzialmente vede) nelle due e quindi può rappresentare solo “una parte” di ciò che esiste nelle tre dimensioni. Se ha davanti a sé una figura a tre dimensioni, ha gli stessi problemi di un abitante dello spazio a due dimensioni. Malgrado tutti gli accorgimenti proiettivi e prospettici, una parte della forma gli è nascosta e la può solo intuire. Pensate quindi alla genialità di un artista come Picasso. Egli ha cercato di rappresentante graficamente una figura inserendo contemporaneamente tutte le sue “facce” anche quelle nascoste alla vista… Ecco perché è stato un Grande, anche se a prima vista sembra aver dipinto solo quadrati e triangoli messi a caso!

Ci stiamo accorgendo di una cosa: cercare di esprimere a parole e anche graficamente la struttura reale e apparente dei vari spazi è impresa abbastanza laboriosa, piena di risvolti segreti e/o ambigui. Quando invece passiamo alla descrizione matematica tutto diventa rapido e banale.

E’ facile dimostrarlo. Prima di discutere il risultato dello spostamento del 2-cubo per ottenere il 3-cubo, cerchiamo di prevederlo con le regole “matematiche” precedenti:

Quante facce ci saranno nella nuova figura?

Beh… le facce originarie (quadrati in questo caso) sono sempre due. Le dimensioni sono 3 e quindi:

3 x 2 = 6 facce totali.

Funziona! Il 3-cubo ha proprio sei facce quadrate, ossia sei 2-cubi. Abbiamo ottenuto proprio quello che siamo abituati a chiamare cubo. Il risultato è chiarissimo (malgrado l’ausilio delle proiezioni) anche nella Fig. 3.

All’interno di questa nuova figura vi è adesso uno spazio V che è proprio dato da L³. Come si calcola la parte interna alle facce? Nel caso dell’1-cubo era la lunghezza del segmento tra le due facce (P e P’), ossia L. Nel caso del quadrato era L volte il lato (la faccia) L, ossia L². Adesso sarà L volte la faccia L² (il quadrato), ossia proprio il volume L³. La matematica è meglio di tante parole…

Riportiamo uno schema ancora più rigoroso e sintetico, aggiungendo un altro parametro P, l’estensione totale delle facce. In altra parole, i due punti dell’1-cubo, il perimetro del 2-cubo e la superficie del 3-cubo.

Dimensioni  Nome comune   Tipo di faccia    No di facce     V          P

1                         segmento                  punto                       1 x 2 = 2         L      2 punti

2                         quadrato                 segmento                  2 x 2 = 4         L²       4L

3                            cubo                      quadrato                   2 x 3 = 6         L³       6L²

La matematica non ha avuto alcun problema… La geometria e il disegno qualcuno in più, ma ancora risolvibili abbastanza facilmente.

La Figura 4 ci fa vedere molti cubi proiettati su un piano. Come già detto e ridetto, ogni volta si è costretti a sacrificare qualcosa, anche se, vivendo nelle tre dimensioni, riusciamo a comprendere facilmente cosa rappresentano quelle strane figure. E’ il nostro cervello che permette di legare ciò che esiste realmente nelle tre dimensioni e capire subito quello che abbiamo raffigurato nel piano del foglio. Così come è solo il ragionamento a permettere di riconoscere un quadrato a chi vive nelle due dimensioni e può rappresentarlo solo su una dimensione. E così pure per chi vive nella singola dimensione.

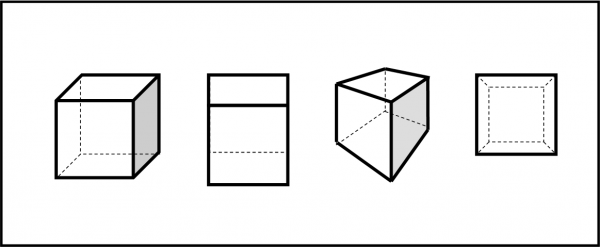
Possiamo usare, tra le tante, una prospettiva centrale (ultima immagine a destra della Fig. 4), nel caso che si abbia una faccia (quadrato) vista proprio di fronte. Si disegna il secondo quadrato (la faccia opposta) più piccola (tenendo conto che le distanze appaiono più piccole se si allontanano da noi).  e si uniscono di nuovo gli spigoli. Questo tipo di rappresentazione può “apparentemente” semplificare il prossimo passaggio.

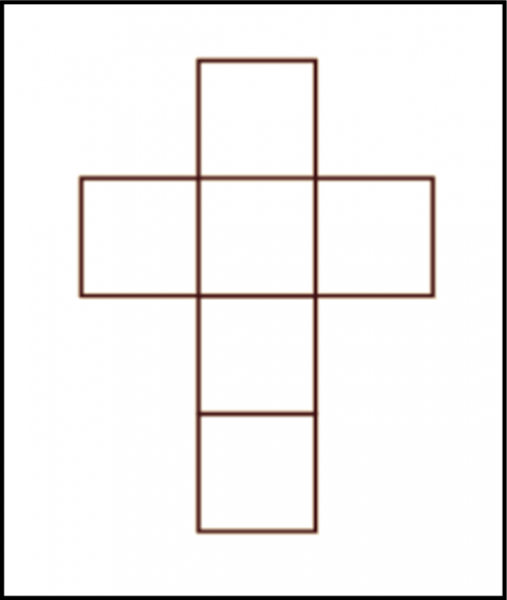
Esiste, poi, un altro sistema per rappresentare un 3-cubo nelle due dimensioni. Basta distendere o -meglio- sviluppare completamente la sua superficie esterna sul piano. D’altra parte, ogni faccia del 3-cubo è un 2-cubo (un quadrato) e, quindi, facilmente rappresentabile nel piano. Otteniamo la Fig. 5, ben conosciuta da tutti! Il 3-cubo si è aperto e, usando forbici e colla, la figura può permettere di ricostruire il 3-cubo nelle sue tre dimensioni. Beh… abbiamo fatto un po’ come Picasso, anche se in modo molto “freddo” e schematico. Questa figura ci permetterà di chiacchierare a lungo sulla casa a quattro dimensioni…

Adesso viene il bello. Lasciamo da parte le impressioni visive e pensiamo alle regole matematiche che abbiamo dedotto precedentemente. Attenzione. Stiamo per introdurre la quarta dimensione, ma non pensatela come “tempo”. Pensiamola solo e soltanto come una dimensione in più. Ci basta e avanza. Riprendiamo la tabella riportata prima e aumentiamo tutto di una dimensione. Ci vuole ben poca fantasia per scrivere le grandezze previste:

Dimensioni   Nome comune  Tipo di faccia   No di facce        V           P

1                         segmento                  punto                   2 x 1 = 2               L         2 punti

2                         quadrato                segmento               2 x 2 = 4               L²           4L

3                             cubo                    quadrato                2 x 3 = 6               L³           6L²

4                          ipercubo                   cubo                     2 x 4 = 8               L⁴           8L³

Il 4-cubo ha otto facce, ciascuna formata da un 3-cubo. Il suo volume V è L volte il volume L3 della singola faccia. Il perimetro P è dato dall’estensione di una faccia moltiplicata per sei.

La matematica ha risolto il problema delle 4 dimensioni con un facilità irrisoria e non avrebbe problemi a passare anche alle cinque o n-dimensioni…

n                            n-cubo                   n-1cubo                2 x n = 2n            Lⁿ         2nL^n-1

Non è nemmeno difficile calcolare, attraverso semplici formule e con la stessa facilità, come varia il numero totale degli spigoli, dei segmenti, dei quadrati, dei cubi, di volta in volta. Meraviglia della matematica! Con questi dati saremmo in grado di sviluppare tutta una serie di operazioni, di proiezioni, di confronti con qualsiasi spazio. Capite perché non vi è nessun problema a far girare programmi al computer in cui si ipotizzano spazi a n-dimensioni? Tutto si basa su una regola ripetitiva e ben conosciuta.

Potremmo anche fermarci qui, dato che abbiamo risolto matematicamente il problema. Tuttavia, siamo tutti un po’ come San Tommaso e vorremmo vedere e/o toccare con mano, finché, ovviamente, i nostri sensi riescono ad aiutarci. In particolare, dobbiamo ancora far vedere come ottenere graficamente un 4-cubo… seguendo la solita procedura. Ahi, ahi, qui casca l’asino…

Innanzitutto, dobbiamo ammettere che non siamo in grado di girare attorno a una figura a quattro dimensioni. Il tatto e altre cose del genere sono inutili. Dobbiamo affidarci completamente al cervello e alle sue intuizioni. Seguendo la strategia utilizzata finora dovremmo, infatti, prendere un cubo (la faccia del 4-cubo) e disegnarlo (e fin qui niente di veramente difficile). Poi, però dovremmo spostarlo lungo la quarta dimensione. E qui veramente andiamo in completa crisi. Dov’è e qual è la quarta dimensione? Non esiste prospettiva o proiezione che ci possa aiutare.

L’unica cosa che possiamo fare è costruire una proiezione del 4-cubo nelle tre dimensioni. Ossia cercare di vedere quello che si può vedere girando nelle spazio a tre. Inoltre, dato che sappiamo disegnare ogni forma del mondo a tre dimensioni in uno spazio a due, potremmo addirittura disegnare, in uno spazio a due dimensioni, una proiezione a tre dimensioni di una figura a quattro dimensioni. E’ proprio quello che cercheremo di fare!

Tenetevi forte e cominciamo. Innanzitutto, è meglio mostrare il procedimento, tornando allo spazio a due dimensioni e vedere come i suoi abitanti (pallini rossi) potrebbero intuire una figura a tre dimensioni, ossia una figura con una dimensione in più della loro.

Accidenti. Hanno già problemi a rendersi conto del quadrato e vogliamo fargli “intuire” il cubo? Sì, in qualche modo è possibile.  La Fig. 6(a) ci mostra un 3-cubo, disegnato in uno spazio a due. Per gli abitanti rossi la visione di questa figura non è altro che un normale quadrato: si vedrebbe solo la sezione del 3-cubo con lo spazio a due. Due osservatori rossi, posti a 90° tra loro, ossia lungo le due uniche dimensioni possibili, lo inquadrerebbero abbastanza bene. Adesso facciamoli lavorare nel loro piano e facciamogli applicare la solita strategia che porta a una figura con una dimensione in più. E’ come se proiettassero,  in qualche modo, la costruzione del 3-cubo nelle due dimensioni, dove esistono solo quadrati.

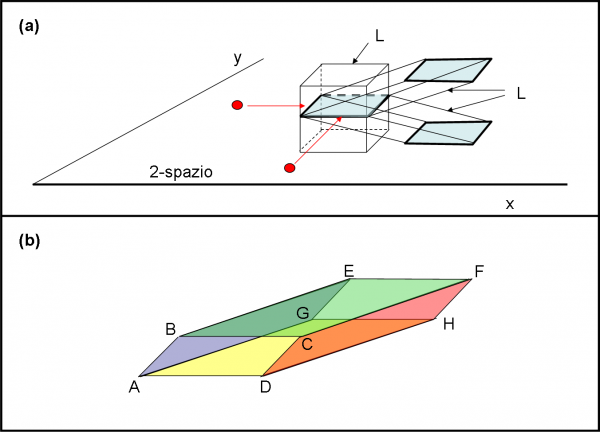
I nostri pallini rossi spostano il quadrato, che intuiscono abbastanza chiaramente, di una certa distanza L (sempre la solita). Per non pasticciare troppo la figura, permettetemi di allungare un po’ questa L, se no i quadrati si sovrappongono ed è più difficile capirci qualcosa. Vediamo nella figura due casi di questo tipo. State attenti che ogni nuovo quadrato azzurro giace sempre nel piano xy. Dopo aver eseguito lo spostamento, risulta abbastanza semplice unire con delle linee i corrispondenti spigoli dei due quadrati.

Ebbene, se i pallini rossi sono intelligenti hanno capito di avere ottenuto una proiezione del cubo con tutte le sue caratteristiche misurabili! Guardiamo meglio l’unione di due quadrati azzurri nella Fig 6(b). Ho usato colori diversi e indicato i vertici dei due quadrati. Ebbene, si possono riconoscere, sempre e soltanto nel piano xy, le sei proiezioni dei quadrati (facce) che compongono il 3-cubo. Essi sono ABCD, EGFH, ABEG, BEFC, FHCD, GHAD. Abbiamo ottenuto una rappresentazione (ossia una proiezione) di un cubo a tre dimensioni in un piano a due dimensioni. La stessa cosa, in modo grafico un po’ più confuso, potrebbe essere fatto per descrivere un 2-cubo nello spazio a una dimensione. Provateci, non è certo difficile…

Perché abbiamo fatto questo lungo discorso? Perché a questo punto possiamo applicare lo stesso procedimento anche per una figura dello spazio a quattro dimensioni. Senza bisogno di conoscere dove sia la quarta dimensione, possiamo trovare una proiezione, con tutte le caratteristiche più evidenti, nello spazio a tre. Basta imitare i pallini rossi dello spazio a due dimensioni. Anche loro non conoscevano la terza dimensione, ma sono riusciti ad avere una completa (o quasi) rappresentazione del 3-cubo nel loro mondo ultra limitato. La forza del cervello… quando è usato bene!

Consideriamo la Fig. 7. Immaginiamo che essa sia proprio uno spazio a tre dimensioni, come quello che ci circonda. Sarebbe, infatti, molto meglio costruire un 3-cubo e spostarlo fisicamente, ma noi ci accontentiamo di rappresentare il tutto nelle due dimensioni del foglio, utilizzando le ben note regole prospettiche e/o proiettive. Disegniamo un 3-cubo e spostiamolo lungo una dimensione (o una qualsiasi combinazione delle tre dimensioni conosciute). Nuovamente, dovremmo spostarlo della lunghezza L, ma noi la esageriamo per chiarezza di figura.  Otteniamo una bellissima figura, magari un po’ complicata (sarebbe meglio vederla proprio scolpita in tre dimensioni), ma interpretabile abbastanza bene con un po’ di pazienza. E’ inutile che provi a colorarla o a indicarne gli spigoli. Con un po’ di ragionamento e di riflessione si riescono a scorgere gli otto 3-cubi che delimitano il 4-cubo. Ovviamente, due di questi hanno ancora la forma del cubo che conosciamo, mentre gli altri sono profondamente deformati. D’altra parte stiamo rappresentando, in due dimensioni, una proiezione nelle tre dimensioni di una forma a 4 dimensioni!

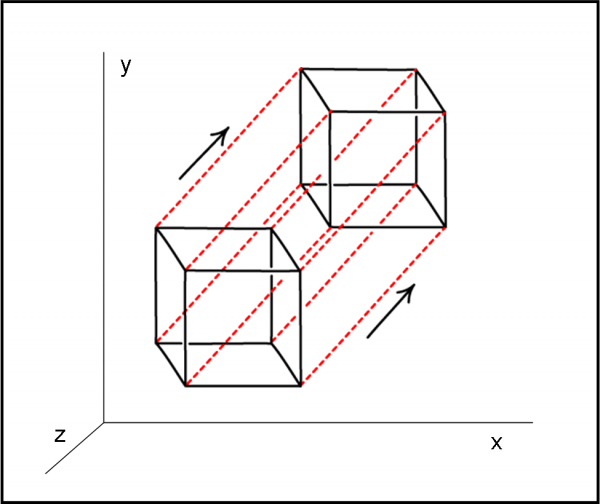
Possiamo, però, usare direzioni di vista molto diverse: vivendo nello spazio a tre dimensioni, è ammesso spostarci in alto e in basso, a sinistra e a destra, verso l’osservatore e in direzione opposta. Inoltre, abbiamo a disposizione varie tecniche proiettive. Una delle rappresentazioni migliori del 4-cubo si ha usando una specie di prospettiva centrale. Consideriamo la Fig. 8. Prendiamo un cubo e spostiamolo verso il suo interno facendolo diventare più piccolo. Poi uniamo i vertici corrispondenti. Oltre ai due cubi originali, si notano abbastanza bene i sei cubi “deformati” (facce) che sono raffigurati come tronchi di piramidi quadrate (ad esempio ABCDEFGH), che circondano da ogni parte i due cubi di partenza.

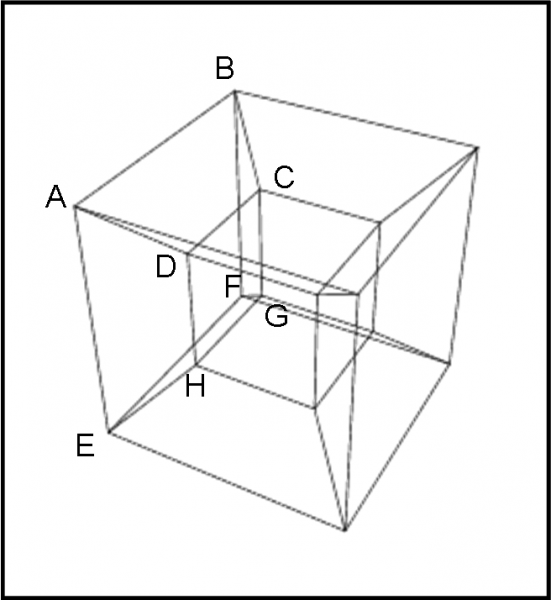
Malgrado le ovvie deformazioni subite, possiamo concludere di aver capito che un 4-cubo o ipercubo (o anche tesseratto) è una figura a quattro dimensioni che ha, come facce che lo delimitano, otto cubi a tre dimensioni.  Inoltre -e soprattutto- siamo riusciti a disegnarlo. La matematica ce l’avevo detto in modo semplicissimo, la geometria e il disegno hanno dovuto lottare molto di più.

“Cosa” sia contenuto all’interno di queste otto facce cubiche va al di là della nostra immaginazione. E’ uno spazio a quattro dimensioni e non possiamo pretendere di “vederlo”. Siamo stati, però, in grado di disegnarne (in due dimensioni) le facce (a tre dimensioni) che lo contengono. Non è certo stata operazione da poco.

Possiamo anche usare un differente approccio che ci verrà utile tra poco. Vi ricordate la Fig. 5? Bene, non ci resta che “aprire” un ipercubo nello spazio a tre dimensioni e poi proiettarlo nel piano del foglio. Ottengo la Fig. 9. Gli otto cubi che formano la “superficie” esterna dell’ipercubo sono perfettamente quantificabili e visibili. Non possiamo però chiedere a qualcuno di ritagliarli e di ricostruire la figura a quattro dimensioni. Accontentiamoci, comunque, di questa rappresentazione.

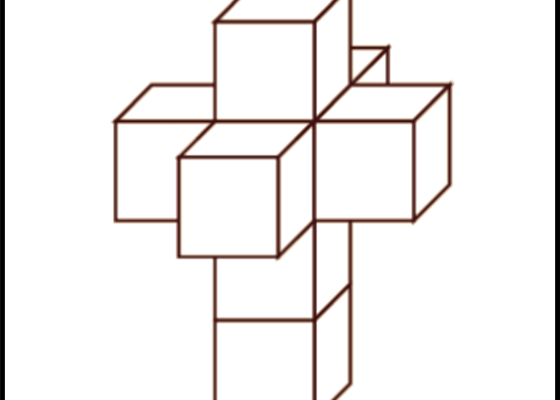
In realtà, sarebbe facile costruire una scultura o un edificio che permetta di toccare direttamente la “superficie” esterna dell’ipercubo (un solido in questo caso, dato che le superfici esterne sono composti da cubi).  Salvator Dalì lo ha rappresentato in sua celebre Crocifissione (Fig. 10). Torneremo su questo discorso tra pochissimo.

Cari ragazzi, ho usato un metodo abbastanza personale per arrivare a una conclusione che spero “sufficientemente” comprensibile. Ci sono altri metodi, ma questo mi sembrava il migliore. Se qualcuno, però, chiedesse di vedere le cose in altro modo, potremmo sempre cercare di aggiungere un’altra strategia operativa.

Adesso, però, cerchiamo di divertirci un po’, richiamando i due libri di cui ho parlato all’inizio. Molti dei problemi affrontati dagli abitanti degli spazi a varie dimensioni sono descritti umoristicamente in Flatlandia. In quel caso, gli abitanti delle due dimensioni hanno anche avuto l’aiuto di un abitante delle tre che gli ha fatto scorrere un cubo (e non solo) lungo la “sua” terza dimensione, mostrandogli come variavano le sezioni bidimensionali che loro potevano vedere o intuire. Un modo molto simpatico, ma non facile a rappresentare graficamente. Leggetelo, quindi, e vi aiuterà a comprendere ancora meglio questo articolo o -magari- il viceversa.

Voglio invece concludere riallacciandomi alla Casa Nuova di Heinlein.

Iniziamo da lontano… immaginiamo che un abitante dello spazio a due dimensioni voglia stupire il suo mondo e costruire una casa a tre dimensioni. E’ un ricco magnate e affida l’impresa a un architetto di grande intuizione e immaginazione. Ovviamente è impossibile costruirla fisicamente, ma si può sempre costruire una sua proiezione, come quella di Fig. 6(b) o ancora meglio quella di Fig. 5. Il riccone avrebbe a disposizione una banale casa a due dimensioni che però rappresenterebbe la proiezione di una casa a tre dimensioni.

Nessun problema ad abitarci: in fondo è sempre e soltanto un edificio steso sul piano xy. Le porte di uscita potrebbero essere, ovviamente, solo lungo i lati (segmenti), dato che non si può uscire dalle facce quadrate perché vorrebbe dire andare verso l’alto o il basso ed è vietatissimo! Non è proprio comodissima, ma la novità e l’unicità impongono qualche sacrificio pratico. Alcune stanze sono raggiungibili solo attraversando altre stanze, ma va beh… l’inconveniente sarebbe ampiamente compensato dal pensiero di vivere “ipoteticamente” in una abitazione di dimensione superiore.

Pensate adesso se, per una qualche magia, il cubo così aperto nelle due dimensioni si richiudesse su se stesso nelle tre. Proprio come se lo ritagliassimo e ricomponessimo il 3-cubo. Il nostro povero abitante continuerebbe a vivere in un mondo a due dimensioni, ma “ripiegato” nelle tre. In altre parole, potrebbe muoversi solo sulle facce del cubo. Facce che restano abitabili perché a due dimensioni. Non potrebbe, però, uscire verso il loro interno o esterno. L’esterno rappresenterebbe la terza dimensione che gli è proibita. Egli può solo uscire attraverso i segmenti che racchiudono i quadrati (facce). Ma, adesso, non esiste alcun segmento verso un esterno a due dimensioni: ognuno porta in un’altra faccia! La Fig. 11 riassume la tragica avventura.

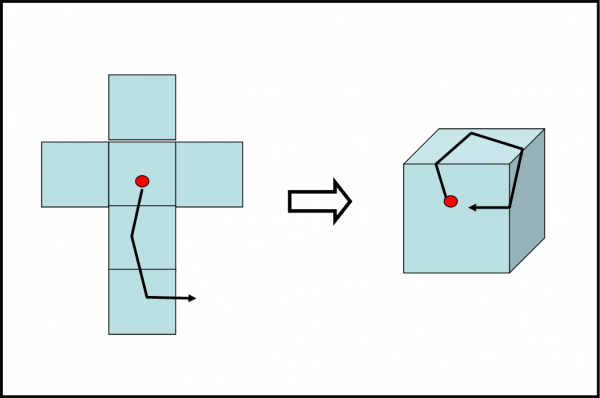
Vi ricorda qualcosa? Magari lo spazio disegnato su una superficie sferica che, all’interno e all’esterno, ha una dimensione come il tempo… una dimensione che non si può toccare e nemmeno calpestare, ma solo rappresentare con la matematica o con l’immaginazione…

Torniamo al nostro riccone in piena crisi. Ogni lato “agibile” porta solo e soltanto in un’altra stanza. Non esistono più porte di uscita. Vivrebbe per sempre sulla superficie esterna di un tre-cubo, senza potere più uscirne fuori!

La stessa cosa, in tre dimensioni, capita al nostro amico del racconto di Heinlein. L’architetto costruisce lo sviluppo su tre dimensioni del 4-cubo. Proprio come la Fig. 9. Otto stanze con comunicazioni e uscite attraverso le pareti quadrate delle singole stanze 3-cubiche (facce). Beh… molto interessante anche se un po’ scomoda: quattro piani e quattro stanze gettate verso l’esterno. Scomoda, forse, ma un’opera d’arte che nessuno ha mai posseduto. La casa, però, si trova in California, terra di terremoti. Ne basta uno leggero e la casa si richiude nelle quattro dimensioni! Ogni quadrato che delimita le facce dell’ipercubo coincide, adesso, con un altro che appartiene a un’altra faccia-stanza. La situazione è simile a quella del riccone a due dimensioni. L’occupante può spostarsi da stanza a stanza attraverso i quadrati che delimitano le stanze (le facce), ma non può più uscire all’esterno o all’interno. Per farlo dovrebbe muoversi nella quarta dimensione. Insomma, ragazzi, un racconto da leggere: il divertimento è assicurato!

Mamma mia… che fatica! Ho cercato di non dimenticare niente e di immedesimarmi in chi legge questo tipo di proiezione per la prima volta. Se vi fossero punti oscuri, mi raccomando… ditemelo subito. Sarebbe un peccato non riuscire ad afferrare in pieno le varie strategie operative e il concetto nel suo insieme. Mi devo riposare un po’…

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI l'approfondimento dedicato alla Relatività Generale

QUI un viaggio nelle n-dimensioni da Dante Alighieri ad Albert Einstein, passando per Bernhard Riemann