A furia di tirar pietre

Mettiamoci, quindi, sul corpo O e proviamo a lanciare la nostra pietra P. Per lanciarla, dobbiamo, ovviamente, impartirle una certa velocità, che è l’unica cosa che riesce a far muovere una massa m. Per fare ciò impartiamo con il braccio una forza F alla pietra che si trasforma in un’accelerazione che, a sua volta, origina una velocità. Infatti, la pietra parte con velocità zero, ma, a seguito dell’accelerazione che le abbiamo dato, passa a una velocità v diversa da zero. Ricordiamo che l’accelerazione crea una differenza di velocità dv in un certo intervallo di tempo dt. Acquistare una velocità vuol dire permettere al corpo P di spostarsi di uno spazio ds in un intervallo di tempo dt, anche se lungo una traiettoria rettilinea (accelerazione tangenziale). Otteniamo, praticamente, un moto.

Ovviamente, l’accelerazione dura un attimo, quello che basta per regalare la velocità v (costante) alla pietra P. A questo punto il sasso si sta muovendo di moto rettilineo uniforme, cercando disperatamente di allontanarsi dal corpo O. La faccenda non è certo semplice, dato che P è costretto a muoversi all’interno della ragnatela creata da O. Cosa succede, in pratica? La pietra è soggetta a una velocità che è obbligata a deviare la sua direzione e a cambiare il modulo sotto l’azione dell’accelerazione di gravità. Se disegnassimo una figura simile a quelle descritte nella puntata scorsa, avremmo una soluzione drammatica: la pietra cadrebbe su O, in breve tempo (Fig. 12).

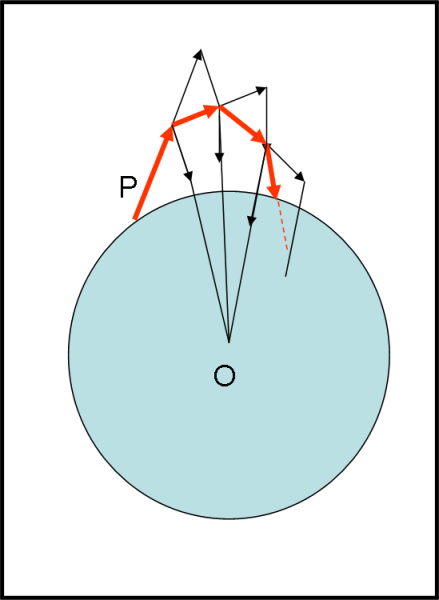
Non sarebbe difficile descrivere questa traiettoria, dato che è una parabola come quella descritta da un proiettile sparato da un cannone. Proprio attraverso un cannone molto più potente, potremmo aumentare la velocità della pietra. In questo modo ritarderemmo la sua caduta. Non basta ancora? Beh… perché non usare una rampa di lancio per missili e sparare il sasso nello spazio? Potremmo ottenere una velocità tale che la pietra si metta in condizioni di stallo rispetto alla ragnatela. Non è certo difficile ricavare la velocità necessaria: l’abbiamo già visto la volta scorsa.

Quando raggiungiamo questa velocità, l’accelerazione diventa puramente centripeta, dato che la velocità è sempre tangente a un cerchio di centro O. Agendo dal “di dentro”, abbiamo, perciò, ottenuto lo stesso stallo dell’altra volta, descrivendolo in modo diverso. Siamo riusciti a lanciare una pietra che continua a girare attorno a O. In realtà, essa continua a cadere verso di lui (la velocità si piega verso il basso), ma non lo raggiunge mai. Magnifico!

Per farvi capire la semplicità e profondità di questo processo mentale, basta inserire la Fig. 13, disegnata proprio da Newton per spiegare il concetto generale. Se spariamo con le modalità giuste, la pietra raggiunge la giusta velocità e la caduta non si verifica più. La pietra resta sospesa a galleggiare ruotando nella ragnatela di O. Il caso riportato da Newton usava proprio la velocità tangenziale fin dalla partenza. Essendo su una montagna altissima si poteva sparare in direzione orizzontale ed essa era già quella giusta per entrare in orbita.

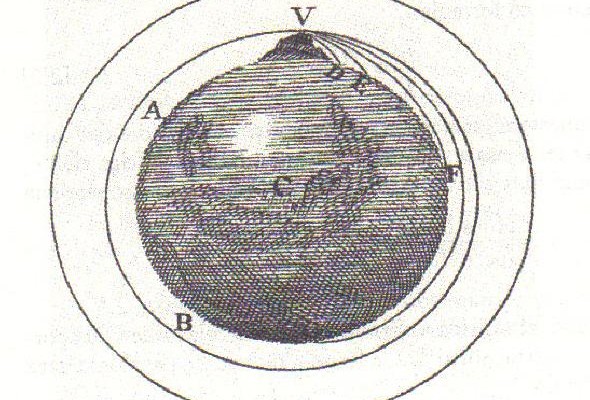
Quando si lanciano i satelliti si spara verso l’alto e quindi la velocità necessaria  si ottiene dopo che l’accelerazione della ragnatela l’ha costantemente deviata fino a che non sia diretta perpendicolarmente alla direzione PO. In parole più tecniche si parla di orbita di trasferimento (Fig. 14), ma lasciamo perdere se no Lampo ci picchia! Sciocchezze, comunque, per i “cannoni” di oggi. Resta il fatto che la Fig. 13 è un vero capolavoro. Pensate che è stata ideata senza ancora conoscere la legge di gravitazione universale. Anzi è stata proprio usata per dimostrarla!

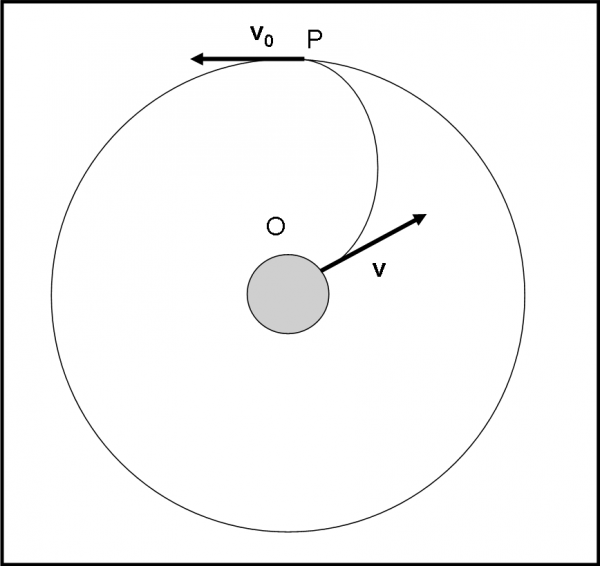
Qualcuno potrebbe chiedermi: “Sì, sì, tutto molto bello… ma cosa cambia rispetto alla volta scorsa? Abbiamo ottenuto le identiche formule del moto circolare uniforme!”. Avrebbe sicuramente ragione (d’altra parte volevamo proprio quello), ma siamo NOI questa volta a cercare di dare alla pietra la velocità giusta e non sperare solo che il corpo che viene da fuori riesca ad ottenerla per puro caso. In poche parole, abbiamo scelto NOI la velocità necessaria a mettere sicuramente la pietra-satellite in orbita e anche all’altezza che vogliamo raggiungere. Non abbiamo aspettato che la lotta tra la velocità di un corpo esterno e la ragnatela decida se e dove il corpo P può mettersi in moto circolare uniforme. Abbiamo preparato a tavolino la nostra difesa!

Come appena detto, non solo abbiamo la sicurezza della riuscita della missione, ma possiamo anche scegliere l’altezza che vogliamo raggiungere: basta, infatti, cambiare la velocità! Se la v, tangente al cerchio, cresce, la formula ci dice che anche la distanza r da O deve crescere. E tutto ciò lo otteniamo, qualsiasi sia la massa che mandiamo verso lo spazio. Un attimo, un attimo. L’unico momento in cui la massa da inviare gioca un ruolo decisivo è all’atto della forza da imprimere al sasso-satellite per farlo muovere alla giusta velocità. La forza necessaria a dargli la giusta accelerazione, e quindi velocità e spostamento, dipende (e come!) dalla massa m da inviare nello spazio (é o non è F = ma, secondo principio della dinamica?).

OK, OK, siamo capaci di inserire in orbita tutte le pietre che vogliamo, ma cosa c’entra con la Luna? Ebbene, una Luna che viene “da fuori” avrebbe una velocità “di crociera” frutto del suo passato. Una che viene “da dentro” sarebbe composta da materiale (tante pietre) che partono da O con velocità molto diverse tra loro. Molte ricadrebbero perché la velocità è troppo bassa. Altre se ne andrebbero nello spazio perché la velocità è troppo alta. Ma moltissime si sistemerebbero su orbite circolari, avendo raggiunto la giusta velocità per ottenere lo stallo a una certa distanza. Insomma, si creerebbe un disco di materia, come il disco che si è formato attorno al Sole. A quel punto giocherebbe la velocità relativa (piccola) tra le varie pietre ed esse inizierebbero a scontrasi tra loro diventando un corpo sempre più grande. La gravità della prossima Luna riuscirebbe a vincere quella del lontano corpo O. Due insetti innamorati, intrappolati in due punti molto vicini della ragnatela, non riuscirebbero a scappare, ma potrebbero muoversi quel poco che li farebbe sopravvivere uniti nella loro configurazione di stallo. Ricordiamo, infatti, che pur aumentando la massa della proto Luna non cambierebbe assolutamente l’accelerazione-ragnatela di cui è vittima.

Ricapitoliamo: lavorando dal “di dentro” potremmo non solo scegliere volontariamente la velocità necessaria allo stallo (satelliti artificiali), ma anche aspettarci che le pietre, scappate in modo naturale dopo un impatto catastrofico, riescano a coprire un intervallo di velocità tale da contenere anche quelle giuste per avere un moto circolare uniforme. Non una sola velocità decisa “da fuori”, ma un “range” enorme di velocità tra cui selezionare quelle adatte a sopravvivere per sempre nella ragnatela.

In questo secondo caso, molto più realistico, potremmo proprio dire che la Luna continua a cadere verso la Terra, ma ritarda all’infinito il momento dell’impatto.

Abbiamo quindi risposto alla domanda iniziale: la Luna continua teoricamente a cadere verso la. Terra, ma la stessa ragnatela, che cerca di trascinarla verso di noi, le permette di non cadere mai. Tutto ciò sempre, e comunque, senza attriti, perturbazioni ed effetti mareali dovuti a corpi non perfettamente rigidi. Ma questo è tutto un altro discorso che abbiamo già affrontato varie volte.

La reazione c’è ma non si vede

Come avete visto abbiamo ottenuto un moto circolare uniforme senza mai fare entrare in ballo altre forze che non siano quella di gravitazione universale, che si traduce nell’unica accelerazione esistente, quella centripeta. Escludiamo, infatti, quella necessaria a lanciare il corpo nello spazio, dato che agisce solo per un istante e poi scompare immediatamente.

Tutto questo giallo ha un finale essenzialmente positivo per entrambi i contendenti. La massa O riesce a non farsi scappare il corpo P e quindi la sua ragnatela funziona. Il corpo P riesce a non essere inghiottito e a trovare una situazione di pacifica sopravvivenza. Tutti felici e contenti. Non potendo ottenere il massimo, ci si deve accontentare di una via di mezzo che in fondo regala soddisfazione a entrambi gli avversari, ossia al mandante e alla vittima.

Tuttavia, immaginiamo che l’intero dramma (o meglio commedia…) sia vista da un alieno di passaggio (che si tiene a debita distanza dalla ragnatela, che non guarderebbe in faccia nessuno). Cosa conclude? Un corpo P è riuscito a girare attorno a un corpo O di massa ben più grande sotto l’effetto di un’unica forza, quella che cerca di attirarlo verso O. Una forza che dà luogo a una sola accelerazione. L’accelerazione è centripeta e tale è anche la forza che la crea.

Ma dov’è finito il terzo principio della dinamica? Dov’é la reazione uguale e contraria che la massa m deve esercitare per ribellarsi alla forza della massa M? Insomma, non esiste nessuna “vendetta”? C’è, c’è, non preoccupiamoci. E, a questo punto, bisogna leggere bene il terzo principio. Esso dice che se P subisce una forza, si vendica applicando a O una forza uguale e contraria. Capito il concetto fondamentale? La reazione non si applica a P, ma a O.

In realtà, O subisce una forza uguale e contraria a quella che esercita su P, ma l’accelerazione che cerca di smuoverlo, e quindi il suo spostamento, è troppo piccolo per essere notato. Infatti, l’accelerazione di O nasce dalla stessa forza di gravità che agisce anche su P, ma deve essere divisa per M. Ciò che resta è, quindi, un’accelerazione ridicola e praticamente invisibile. In altre parole, anche P crea la sua piccola ragnatela, ma il corpo O se ne ride bellamente e non ci pensa nemmeno.

Ciò non è più vero quando le masse diventano comparabili, dato che la reazione diventa ben visibile e misurabile. Il moto circolare si complica (apparentemente, perché lui resta sempre lo stesso), facendo girare entrambe le masse attorno a un punto particolare, un punto che è come la Svizzera durante i conflitti mondiali, un punto del tutto neutrale, capace di proseguire nel suo moto rettilineo uniforme rispetto al sistema inerziale degli alieni. Parliamo, ovviamente, del baricentro… ma evitiamo di approfondire la questione, se no saremmo obbligati a introdurre energie, momenti angolari e … tutta la meccanica classica. Torniamo alla nostra pietra che gira attorno alla Terra. Ne abbiamo a sufficienza di cose da dire!

Una forza che non esiste! Parola degli alieni…

Ricapitoliamo il pensiero degli alieni. La pietra è soggetta solo e soltanto alla forza o –meglio- all’accelerazione centripeta. Non vi sono altre accelerazioni e, di conseguenza, nessun’altra forza in gioco (ricordiamo ancora una volta che l’esistenza di una forza implica un’accelerazione e l’esistenza di un’accelerazione implica l’esistenza di una forza: non possono mai esistere separate!). E’ solo lei che causa una variazione nel moto di una pietra qualsiasi, che altrimenti se ne andrebbe tranquillamente secondo il primo principio della dinamica, ossia con un pacifico e inoffensivo moto rettilineo uniforme.

Insomma, cari ragazzi, non esiste nessuna forza centrifuga. Non ce n’è assolutamente bisogno. Tutto è stato spiegato perfettamente e lei non ha mai fatto la sua comparsa. Essa NON è certamente la reazione alla forza gravitazione (ossia centripeta) che attrae il corpo P verso O. La reazione, sempre esistente, ma praticamente invisibile nel caso Terra-pietra,  viene applicata su O e deve essere considerata anch’essa una forza centripeta diretta da O verso P.  Tenete ben presente questo concetto per non fare confusione quando parleremo di forza centrifuga. Sì, ne parleremo, anche perché non possiamo certo far finta di niente e cancellarla da tutti i libri!

Senza peso, ma non senza forza

L’ affrontiamo in modo indiretto, in modo da sfatare un altro possibile fraintendimento, che, a volte, viene proprio creato da qualche professore…  Immaginiamo che la nostra pietra sia una navicella vuota al cui interno vi sia una pietra più piccola o -se preferite- un  astronauta. Che bello vederlo galleggiare nella capsula senza peso. Beh…. ovvio… è talmente distante dalla Terra che non risente della sua gravità. Mamma mia, che errore grossolano! (E la Luna, allora, che è ancora più distante?). Se fosse così, come mai la capsula spaziale continua a girare attorno alla Terra in balia della sua accelerazione gravitazionale? No, no, la ragnatela c’è ancora, statene certi. La mancanza di gravità non è assolutamente dovuta alla distanza. Ci vorrebbe ben altro.

Il fatto è che l’astronauta ha la stessa velocità della capsula e quindi rispetto a lei non si muove: subiscono entrambi, astronauta e capsula, la stessa accelerazione. In altre parole, ancora: se l’astronauta si sente senza peso, la stessa cosa sente anche la navicella (potesse parlare, lo direbbe!). Se la corda di un ascensore si rompe, siete o non siete costretti a cadere insieme a lui. Restate sempre al vostro posto rispetto all’ascensore, ma alla fine vi schianterete come lui! Se il satellite dovesse improvvisamente ridurre a zero la sua velocità orbitale, il povero astronauta sentirebbe, e come, l’accelerazione centripeta che lo porterebbe tragicamente verso la Terra.

L’assenza di gravità per un astronauta è quindi un fenomeno apparente che ci introduce molto bene verso la forza centrifuga. Ricordate, però, che, benché la descrizione fatta dall’astronauta e quella fatta dall’alieno siano nettamente diverse, il fenomeno fisico che avviene è lo stesso. Due modi diversi per raccontare la stessa identica storia. In un caso c’è bisogno di introdurre un certo “mago” per far tornare le cose (ossia per usare sempre le stesse leggi della dinamica), nell’altro assolutamente no. Questa apparente discrepanza ha un solo colpevole, come già detto fin dall’inizio: il sistema di riferimento inerziale! Lui ha le sue regole e non tutti possono seguirle.

Chi gira non è in moto inerziale!

Non ci resta che prendere anche noi una navetta spaziale e raggiungere l’astronauta in orbita. Pensavamo di aver capito perfettamente la situazione e di essere freddi e logici fino in fondo e, invece, ci sentiamo confusi. Accidenti, siamo proprio senza peso e vediamo la Terra girare laggiù sotto di noi. In altre parole, noi ci sentiamo completamente fermi ed è il resto che si muove.

Ma come facciamo a stare fermi se subiamo un’accelerazione centripeta? No, niente da fare. Per stare fermi vuol dire che su di noi agisce un’accelerazione uguale e contraria a quella centripeta. Attenzione però. Non abbiamo bisogno di una reazione uguale a contraria alla forza che ci spinge vero la Terra, ma una forza che annulli quest’ultima. Non è il terzo principio della dinamica di cui abbiamo bisogno, ma solo e soltanto di una forza magica che annulli quella centripeta. Entrambe devono essere applicate su di noi.

In altre parole, per mantenere la nostra posizione immobile, devono agire due forze (o due accelerazioni) che si annullino tra di loro. Solo così possiamo descrivere il nostro stato di quiete (apparente) completa. Questa forza la devo introdurre assolutamente e la chiamo forza centrifuga. Se non lo facessi dovrei stravolgere i principi della fisica e questo non posso farlo.

Va bene, va bene, ma esiste davvero o è solo una nostra invenzione dovuta alla scarsa preparazione fisica? No, signori miei, esiste e come. Ma esiste solo e soltanto nel sistema di riferimento che ruota insieme alla navicella. Per descrivere il nostro moto dobbiamo usare una descrizione diversa da quella dell’alieno. Ma non dobbiamo stupirci più di tanto. E’ una conclusione ovvia: siamo su un sistema di riferimento che non è inerziale, in quanto è soggetto a un’accelerazione e la nostra velocità, benché sia costante come modulo, non è assolutamente costante come direzione. La forza centrifuga ci permette di descrivere in modo diverso un fenomeno che deve essere lo stesso sia per noi che per l’alieno!

Ciò che avviene è esattamente la stessa cosa e anche la legge fisica che lo governa.

Seguitemi in questa dimostrazione “matematica”, poco sfruttata, ma che per me è la migliore possibile. Per mostrarla uso formule che abbiamo già ricavato e usato. Facciamo parlare prima l’alieno e poi l’astronauta.

Alieno: l’astronauta ruota attorno alla Terra con una velocità tale da permettergli di mantenere un moto circolare uniforme. Io sto assistendo direttamente a questo spettacolo e non posso sbagliarmi. Il fatto stesso che la sua traiettoria sia curvilinea e sia descritta con velocità costante mi dimostra che esiste un’accelerazione centripeta che agisce su di lui e questa accelerazione è data da:

a = v²/r

Basta un po’ di cinematica per ottenerla. Se esiste un’accelerazione deve, però, esistere anche una forza che la origina. Essa può essere scritta, in base al secondo principio della dinamica, come

F = ma = mv²/r

dove m è la massa dell’astronauta

Potrei fermarmi qui se non conoscessi Newton e la sua legge. Ma, sono ben preparato e, quindi, so benissimo che questa forza non è altra che la forza di gravità che vale

F = GMm/r²

Posso permettermi di uguagliare le due espressioni precedenti e ottengo:

GMm/r² = mv²/r    …. (1)

Adesso non ho altro da dire, dato che ho espresso ciò che capita con una formula completa che tiene in conto tutte le grandezze in gioco.

Astronauta: Che bella la Terra laggiù in basso! Mi sono addormentato già prima della partenza e non so come sono arrivato fin quassù, ma è veramente una meraviglia. Non sono un grande esperto di fisica, ma ho imparato che a questa altezza (r, come dice la strumentazione di bordo) dovrei subire la forza di gravità della Terra e invece mi sento completamente fermo. Non posso certo essere uscito dal suo campo gravitazionale: se guardo dall’oblò vedo la Luna molto più distante e se lei subisce la gravità della Terra, devo subirla anch’io. Fatemi scrivere la forza di gravità. Fino a lì c’arrivo anch’io:

F = GMm/r².

Insomma, dovrei cadere verso di lei a velocità incredibile e, invece, sono fermo, immobile. C’è una sola spiegazione! In questa navicella in cui mi trovo deve esistere qualche marchingegno che mi permette di non cadere. Da quel poco che ho letto di fisica, so che per poter stare fermo esistono solo due modi: o non sono soggetto ad alcuna forza o la somma di tutte le forze che agiscono su di me deve essere uguale a ZERO. Il primo caso non può andar bene, dato che ho la certezza che esiste la forza di gravità che mi attira verso la Terra. E’ quindi assolutamente necessario che esista un’altra forza, che chiamo F’, che sommata a F dia come risultato ZERO. Non c’è bisogno di essere Einstein per arrivarci. Sono o non sono immobile nello spazio? Tutto è risolto e posso scrivere:

F + F’ = 0

O, tanto per far vedere che non sono poi così ignorante:

GMm/r² + F’ = 0     …. (2)

Ho cercato dappertutto, ma non ho trovato nessun razzo e nemmeno cavi che mi leghino a qualche astronave. Boh … qualcuno prima o poi mi dirà che mistero è mai questo. Magari sono sotto l’effetto di una magia. In un modo o nell’altro, però, sono felice che ci sia. Se guardo verso la Terra mi vengono i brividi a pensare di cadere in picchiata fino a laggiù.

La chiamerei forza della salvezza, qualcosa, insomma, che riesce a non farmi cadere sulla Terra. No, troppo poco scientifico. Un attimo, un attimo… so che la forza gravitazionale è anche una forza centripeta, che vuol dire diretta verso un centro, la Terra o qualsiasi altra massa. E, allora, dato che questa forza è proprio il suo opposto, la chiamerò forza centrifuga, ossia che si allontana dal centro.

Gli astronauti ci scuseranno se li abbiamo presi un po’ in giro, ma era solo per farci raccontare la situazione da uno che non aveva assolutamente idea di ciò che stava capitandogli.

Tocca a noi adesso far vedere che sia l’astronauta che l’alieno hanno detto la stessa identica cosa. Beh… non è certo difficile. La (2) si scrive anche:

GMm/r² = -F’    …. (3)

Affinché la (3) sia uguale alla (1) basta che si abbia

F’ = - mv²/r

La stessa identica legge si ottiene nei due casi (meglio dire “punti di vista”) accettando che la forza centrifuga sia veramente una forza che agisce sull’astronauta, uguale e opposta alla forza centripeta.

Una forza “vera”, perciò, o -quantomeno- realmente avvertita dall’astronauta. Essa è però, in realtà, anche “fittizia” perché serve a spiegare all’astronauta come può stare fermo, immobile, apparentemente senza subire la gravità. L’alieno non ne ha bisogno per spiegare la situazione che vede, l’astronauta invece sì. Se non esistesse  questa forza il povero astronauta cadrebbe sulla Terra. Tuttavia, in questo caso, la legge espressa dalla (1) non si applicherebbe anche al viaggiatore spaziale. Alla fisica non piacerebbe e ancor meno a Newton!

Se leggendo le righe precedenti vi siete sentiti presi in giro, dato che ho detto delle banalità e ho girato sempre attorno alla stessa formula, non arrabbiatevi. E’ il primo passo per capire la differenza tra sistema inerziale e sistema non inerziale. Nel secondo sistema la descrizione deve essere diversa, ma si continua a parlare dello stesso fenomeno.

Capisco, comunque, che, pur avendo seguito e capito i passaggi e i ragionamenti precedenti, alla prima occasione ci si possa trovare nuovamente spiazzati. Vedremo meglio la prossima volta, con casi più “pratici” questa situazione apparentemente assurda nella sua semplicità. Parleremo di giostre, di curve pericolose, di ruote di von Braun e non solo. Magari anche di Coriolis (chi era costui?). E perché non del peso variabile che ha prospettato giustamente Alberto? Nel frattempo, vi lascio un problemino per farvi divertire un po’.

Sapete benissimo quanto vale la velocità necessaria per restare in orbita a una certa distanza r dalla Terra. Sapete anche quanto vale il periodo di rotazione della Terra (24 ore). Vi chiedo, allora: a che altezza deve stare un satellite in modo da rimanere fermo rispetto alla Terra, ossia sempre sopra allo stesso punto della superficie terrestre? Tecnicamente, qual è l’altezza per avere un satellite geostazionario? Avete tutti i dati (rileggete l’articolo precedente) e l’unica incognita è proprio la distanza r… Buona fortuna! Se proprio non ci arrivate… chiedetelo a Caronte, lui è proprio un satellite geostazionario di Plutone… (o è meglio dire plutostazionario?). I “fan” di Plutone non possono non saperlo!

P.S.: mi accontento anche solo della formula risolvente e non del valore numerico. In ogni modo, la costante G vale 6.674 · 10^-11 m³/(kg sec)² e la massa della Terra è = 6 ·10²⁴ kg.