Direi che ormai abbiamo introdotto e capito il vero significato della forza centrifuga, una vera e propria “pezza” che si deve inserire per fare in modo che un fenomeno fisico rimanga se stesso sia in un sistema di riferimento inerziale che in uno rotante. Abbiamo anche capito il ruolo fondamentale dell’inerzia di un corpo, inerzia che si traduce nella sua ferrea volontà di mantenere una velocità costante e un moto rettilineo. La lotta tra ragnatela formata dall’accelerazione di gravità e l’inerzia di un viaggiatore solitario finisce a volte in pareggio. Più facile è ottenere lo “stallo” lavorando dal di dentro, ossia scegliendo come lanciare il viaggiatore. Abbiamo anche imparato che l’assenza di gravità di un astronauta è solo una piccola magia che compie la forza centrifuga o -se proprio non vi piace- la forza centripeta e la velocità che abbiamo dato alla navicella che lo ospita. In fondo è la stessa identica cosa che capiterebbe in un ascensore che venga fatto cadere verso il suolo, tagliando magari le corde. Vi sentireste senza peso, dato che cadete insieme all’ascensore, alla stessa velocità, ma al momento dell’arrivo al suolo vi accorgereste che era solo una impressione e che la gravità esisteva e come!

In generale, però, abbiamo risolto questa doppia faccia della forza centrifuga in un modo che forse ha lasciato un po’ di amaro in bocca. Abbiamo usato formule, facilissime, ma sempre formule matematiche. Come San Tommaso, molti preferirebbero toccare con mano. Dato che non è facilissimo andare direttamente nello spazio a provare l’apparente assenza di gravità vediamo di trovare qualche esempio terra-terra (nel vero senso della parola) che ci metta veramente di fronte a questa “strana” forza che, per chi è in moto circolare, esiste e agisce, ma non per un alieno che assiste da  un’astronave in quiete. Adesso che sappiamo che, in fondo, non esiste, ma è una specie di trucco, saremmo magari convinti di riuscire a farne a meno, o di riconoscere il vero dal falso o -meglio- dal “fittizio”. Rimarremmo molto delusi! Se ci immergiamo in un sistema rotante, la sentiremmo e come! E ne subiremmo anche le conseguenze. Le formule ci sembrerebbero dei ciarlatani che parlano, parlano, ma non sanno quello che realmente capita.

Ho scelto tre esempi, che dicono esattamente la stessa cosa, ma che differiscono nel modo in cui agisce la forza centripeta (l’unica vera forza per l’alieno). Essa, a volte, si nasconde molto bene e lascia spazio libero alla sua amica-nemica forza centrifuga.

Il caso più semplice è quello del lanciatore di martello o  di quelle giostre a seggiolini volanti che fanno ruotare gli audaci (almeno per me) attorno a un palo centrale. Prima di vedere con un semplice schema la situazione, vi faccio una domanda: “Cosa direbbe il “martello” se gli chiedeste dove si sente trascinato?” Sicuramente non avrebbe dubbi: “Verso l’esterno. Meno male che c’è la corda che mi tiene vincolato al lanciatore”. La stessa domanda si può rivolgere a chi sta sul seggiolino della giostra. “Verso l’esterno, accidenti! Verso l’esterno… E non lo dico solo io che sono qui seduto con una paura pazzesca, ma anche il gattino che mi sono messo su una spalla. Le sue unghie piantate profondamente nella carne la dicono lunga: non ha nessuna voglia di essere lanciato verso la folla che ci circonda”.

C’è poco da fare, la forza centrifuga esiste e come! Il caro alieno ha un bel dire che non esiste. Per semplicità annulliamo la forza di gravità che tende a far cadere verso il basso i seggiolini o il martello del lanciatore. In fondo, è solo questione di velocità di rotazione che bisogna imporre all’attrezzo o alla giostra. Caro alieno, dove sarebbe la forza centripeta che comanda la situazione generale? Noi vediamo solo un gatto che cerca di non essere sbattuto fuori dalla giostra!

La Fig. 15 non ha problemi a dare ragione ancora una volta all’alieno, anche se il gatto non si convincerà mai! Il seggiolino ha una certa velocità di partenza che lo porterebbe ad andarsene di moto rettilineo e uniforme, come tutti i corpi di questo magnifico Universo. Chi è che lo costringe a girare come un matto? Solo e soltanto la corda di lunghezza finita. E’ proprio la corda che impartisce la forza centripeta. Una corda non usa la forza gravitazionale che sa lavorare anche a distanza e quindi deve “toccare” il seggiolino. Essa viene applicata direttamente a lui attraverso un contatto diretto che avviene nel punto P. La forza centripeta tende a trascinarlo verso il palo di rotazione. Questa forza genera una reazione uguale e contraria sul palo che si sente tirato verso l’esterno. Nel caso del lanciatore di martello chiedete alla sua mano che strattone subisce! La forza centripeta c’è e basta e avanza per far girare il seggiolino e chi è seduto su di lui (che però si tiene ben stretto), modificandone istante per istante la direzione della velocità.

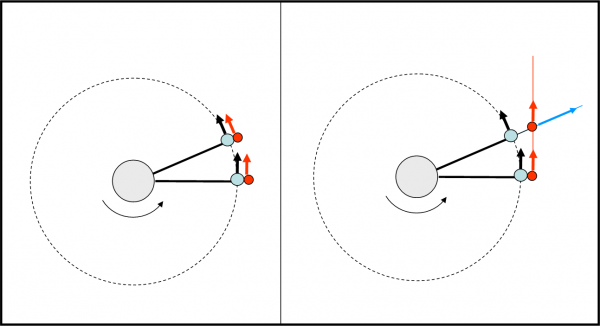
La pallina rossa potrebbe essere il gattino, ma non voglio nemmeno pensarci! Lo sostituiamo con una vera pallina rossa (che ammettiamo, sempre, non subisca la forza di gravità che la farebbe cadere velocemente a terra). Se la teniamo stretta in mano lei viaggia con noi e segue il moto della giostra (a sinistra). Immaginiamo, adesso di lasciarla andare (destra). Per uno che gira sulla giostra la pallina sembra proprio andarsene sempre più lontana, in senso radiale. Può anche misurare in qualche modo la distanza tra lui e la pallina, magari con uno spago o un elastico. Ormai è più che sicuro. La forza centrifuga esiste sicuramente ed è proprio diretta in senso radiale. L’alieno ha torto marcio! Se si slegasse farebbe la stessa fine anche lui. E’ la stessa cosa che succederebbe se qualcuno tagliasse la corda. Il passeggero sarebbe in balia della forza centrifuga dato che è stata abolita la forza centripeta che riusciva a tenerla a freno.

E, invece, l’alieno ha ancora ragione. Per lui, infatti, è successo proprio quello che immaginava. Lasciando la pallina rossa o tagliando la corda, la pallina o tutto il seggiolino (occupante compreso) sono finalmente liberi di andarsene seguendo il tanto amato moto rettilineo uniforme, ossia vanno dritti seguendo la tangente al cerchio che prima la forza centripeta li obbligava a descrivere. D’altra parte, il martello dell’atleta scappa proprio secondo la tangente. Chi assiste all’impresa sportiva allo stadio ne è più che sicuro. Tutti gli spettatori, in quel caso, sono alieni!

Cosa possiamo concludere ancora una volta? E’ il sistema di riferimento che decide se esiste o no la forza centrifuga, ma per chi sta ruotando essa diventa una forza a tutti gli effetti capace di agire direttamente su chi la subisce. Se l’occupante della giostra avesse una borsa al suo fianco sentirebbe e come la forza che cerca di strappargliela di mano! Così come il lanciatore di martello sentirebbe la forza della sfera che cerca di andarsene. L’inerzia è una lottatrice impavida anche quando si trasforma in forza centrifuga!

Il secondo esempio è quello forse più comune: basta andare in automobile su una strada a curve. Nel sedile posteriore c’è sempre qualcosa che può scivolare (magari la solita pallina rossa). Durante una curva verso sinistra il guidatore sente ben poco (è seduto e stringe il volante), ma la pallina inizia ad andarsene verso destra fino a sbattere contro la portiera. Il guidatore sarebbe più che sicuro: la pallina si è mossa perpendicolarmente alla direzione del moto. E invece, il solito alieno, direbbe di no. La pallina ha solo proseguito il suo moto rettilineo uniforme, ossia ha obbedito solo e soltanto alla sua inerzia. La Fig.16 fa capire la situazione molto bene. A sinistra, ciò che “vede” il guidatore; a destra, ciò che realmente succede per un alieno che osserva da un sistema inerziale. Chi ha ragione? Tutti e due, ancora una volta. La forza centrifuga ha agito molto bene sulla pallina (potesse parlare lo direbbe anche lei che è sbattuta violentemente contro la portiera). Qual è in questo caso la forza centripeta, l’unica vera forza osservata dall’alieno? L’attrito delle ruote con il terreno. E’ proprio questo che vieta all’automobile di andare dritta e la obbliga a curvare. Se, infatti, ci fosse del ghiaccio sulla strada vedremmo benissimo come sparirebbe la forza centripeta e … addio curva!. La ruota, ovviamente, si ribella screpolando l’asfalto (il solito terzo principio della dinamica).

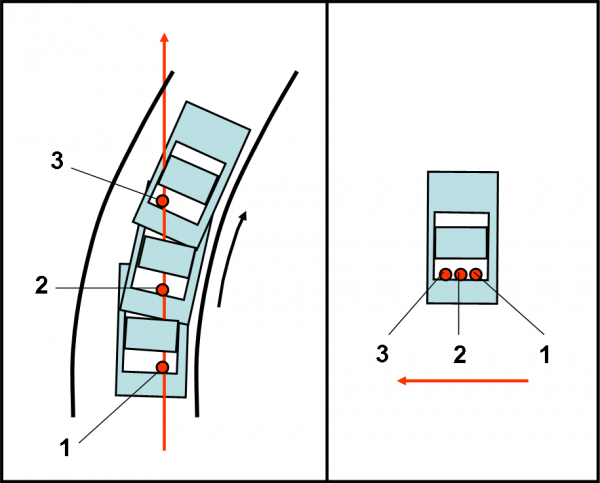
Facciamo attenzione che in questo caso la vettura non esegue effettivamente un moto circolare uniforme (le curve non sono cerchi perfetti) e, quindi, ci sarà anche una componente tangenziale dell’accelerazione che fa variare il modulo della velocità e non solo la sua direzione. In generale, dobbiamo dire che vi è un sistema di riferimento inerziale (alieno) e uno accelerato (non solo ti tipo circolare uniforme) in cui gli stessi fenomeni vanno trattati in modo diverso. Pensate, ad esempio anche solo a un moto rettilineo che subisce un’accelerazione o una decelerazione solo nel senso della traiettoria. Non avremmo curve, ma la velocità cambierebbe continuamente. La pallina rossa non andrebbe di lato, ma avanti e/o indietro, dato che la sua inerzia tenderebbe a farla proseguire di moto uniforme. Perché mai usiamo le cinture? Proprio per evitare gli effetti “locali”, ma ultra reali, di una improvvisa decelerazione. La velocità che avevamo acquisito prima della brusca frenata ci farebbe andare, per accontentare l’inerzia, contro il vetro!

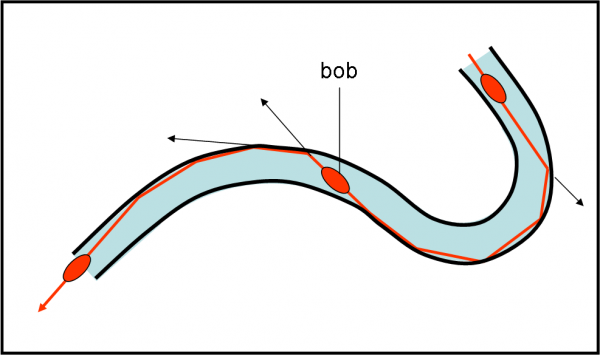
Il terzo esempio riguarda uno sport invernale (ma non solo, ovviamente): il bob o lo slittino. La velocità di discesa è data normalmente dalla spinta e dalla gravità terrestre. Ma, immaginiamo, come al solito, per non complicare la trattazione, che sia solo dovuta a una spinta che riesce a far viaggiare il bob con velocità rettilinea uniforme. Si para davanti una curva a sinistra. Il bob andrebbe tranquillamente dritto, ma la parete della pista lo ferma e piega il bob che -a furia di continui scontri con il ghiaccio- esegue la curva e torna al moto rettilineo uniforme per un breve tratto (magari brevissimo). Altra curva e altro muro di ghiaccio che blocca l’uscita del bob e così via fino alla fine. L’alieno non ha problemi: per lui l’unica cosa che ha evitato la fuoriuscita del bob e gli ha permesso di eseguire le curve è stata la forza centripeta. Basta e avanza. Il muro ghiacciato impartisce la forza centripeta al bob e lo costringe a curvare. Il bob lascia il segno sul muro attraverso delle belle strisciate (tanto per cambiare, per il terzo principio). Chiedete al bobbista una volta che è arrivato in fondo, soprattutto se non è molto bravo ad assecondare le curve con lo sterzo e ad agire sul freno, se si è sentito tranquillo e riposato. Vi dirà, magari ancora balbettando, che ha sentito a ogni curva una forza terribile che cercava di farlo uscire di pista. Forza centrifuga e molto forte anche! Meno male che il muro l’ha annullata.  La Fig.17 mostra la situazione vista dall’alieno. In questo caso è il muro inteso come ostacolo a fare la parte della fune del lanciatore di martello e dell’attrito sulle ruote dell’automobile.

Quest’ultimo esempio ci porta sulla ruota di von Braun, illustrata in Fig. 18. Immaginiamo che sia lontano da pianeti e da stelle, nel vuoto più vuoto che c’è. Tutto è immobile o -più realisticamente- viaggia di moto rettilineo uniforme. Nessuna forza, nessuna gravità e nessun peso. Al suo interno si galleggia liberamente. Non è bello, però, vivere così. Meglio sfruttare la forza centrifuga come una specie di gravità artificiale. Sappiamo benissimo che chi vive all’interno del sistema la sentirebbe sicuramente. Mettiamo in rotazione l’intera ruota fino a che la forza centrifuga (che dipende come sappiamo bene dalla velocità che abbiamo impartito alla ruota) non sia sufficiente a spingere le persone contro la parete esterna. Non poco, ma  nemmeno troppo, se no sai quante “sardine” spiaccicate sulle pareti (e poi dicono che è una forza fittizia!). Si potrebbe benissimo fare in modo di ottenere una gravità uguale a quella che ci regala la Terra, basta agire sulla velocità.

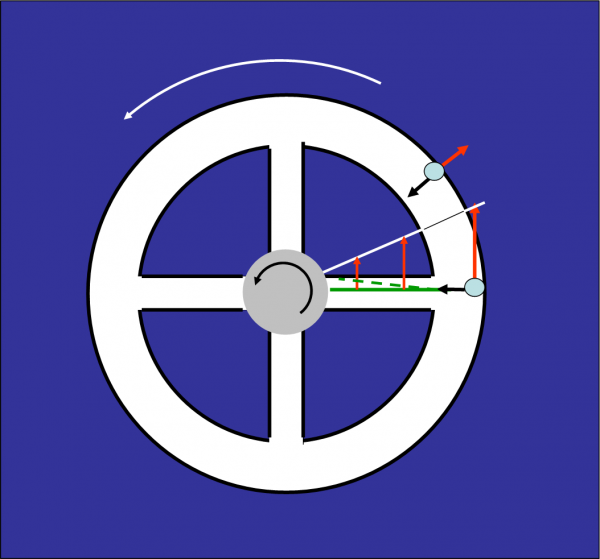
In realtà, l’alieno, che ormai ci perseguita, dice che le persone all’interno della ruota non fanno altro che sbattere contro la parte come il bob di prima. Solo la parete evita che vengano lanciate nello spazio lungo la tangente alla ruota. Le persone, all’interno, invece, si sentono pesanti come a casa loro. Tutto bene? Non tanto, in verità. Immaginate che uno voglia recarsi verso il centro della sfera lungo uno dei quattro raggi-corridoio (magari ci sono i bagni…). Poverino, sarebbe sbattuto contro la parete laterale. Non se lo sarebbe aspettato, dato che non conosceva un’altra forza fittizia (ma per lui MOLTO reale): la forza di Coriolis. Non posso illustrarvi anche questa (vi invito veramente, se siete interessati, ad acquistare la Fisica addormentata nel Bosco…), ma posso solo dire che, andando verso il centro, l’individuo cambierebbe la propria velocità tangenziale (diminuisce la distanza dal centro). La sua inerzia lo porterebbe a continuare come prima e un bella facciata contro il muro del corridoio non glielo toglierebbe nessuno! Meglio prevedere qualche bel cartello che indichi: “Attenzione, Coriolis in agguato!”

Forza fittizia? Sì, sì, ma che dà luogo a un fenomeno che deve esistere anche se visto dal di fuori. Pensate solo ai cicloni terrestri e alle correzioni che deve fare un pilota di aereo che parte da alte latitudini e deve raggiungere basse latitudini. A mano a mano che viaggia, cambia la velocità tangenziale terrestre e nasce … Coriolis.

Volete un esempio più indicativo? Mettetevi su una piattaforma girevole e cercate di giocare a golf. Davanti a voi, sempre sulla piattaforma, c’è la buca. E’ lì, la vedete benissimo, e gira assieme a voi, sempre nella stessa posizione.  Pronti, via, ed ecco un bellissimo tiro. Ma che succede? Siete  sicuramente un vero asso del golf, ma non di fisica. La pallina non va verso la buca, ma compie una curva allontanandosi dalla meta. Che figura! Purtroppo, fareste una figuraccia anche se visto dall’onnipresente alieno. Voi, grande campione, avreste lanciato in modo perfettamente rettilineo, ma mirando un punto ben lontano dalla buca. Che schiappa!

La spiegazione non è proprio banale, ma quasi. Se proprio non volete comprarvi il libro, prima o poi ve la spiegherò… oppure cercate di arrivarci da soli. I mezzi per farlo, in effetti, ce li avete tutti.

Anche vivendo sulla Terra e stando tranquilli in poltrona, siamo soggetti a una forza centrifuga. Non dimentichiamoci, infatti, che il nostro pianeta oltre che a creare la ragnatela gira come una trottola attorno al suo asse. E anche in modo piuttosto veloce, dato che all’equatore percorre ben 40 000 km in sole 24 ore. Bene o male questo fatto implica che, essendo in un sistema rotante, dobbiamo subire una forza centrifuga. Da che cosa è causata? Beh… ormai lo sapete benissimo: per annullare la forza centripeta che ci spinge verso il centro della Terra.

Meno male che la Terra è solida e si rifiuta di accoglierci. Noi, nel nostro piccolo, però, la schiacciamo al massimo delle nostre possibilità. Quanto riusciamo in questo ingrato compito dipende solo e soltanto dalla nostra massa e dalla forza di gravità. Attenzione, non sto parlando di accelerazione, ma proprio di forza e quindi chi ha più massa deve risentire di più della forza di gravitazione.

Essa vale, infatti:

F = GMm/r².

Al variare di m varia la forza che ci attira verso il centro della Terra e quindi anche la forza che noi applichiamo sul suolo. Stiamo, infatti, bene attenti che la forza di gravità sa agire anche a distanza, ma dato che noi calpestiamo il suolo, in questo caso agisce nel punto di contatto con il pavimento, dove lui si ribella e non ci fa passare (terzo principio, come sempre). La forza che noi esercitiamo sul pavimento è proprio la forza di gravità o forza centripeta. Normalmente la chiamiamo anche forza peso p e indica il peso di ciascuno di noi. Attenzione, quindi: il peso p è una forza. Se è una forza dipende dalla massa m, ma può cambiare indipendentemente dal suo valore, dato che compare anche la massa M e la distanza r. Anzi possiamo dire che il rapporto tra peso e massa di un corpo è proprio l’accelerazione di gravità. Infatti:

p/m = GMm/mr² = GM/r² = g

Chiamiamo l’accelerazione di gravità al suolo g, dato che è una costante se il corpo che la genera (g è un’accelerazione e quindi fa parte della ragnatela) è perfettamente sferico e omogeneo. Diciamo, normalmente, che g è una costante anche per i corpi che cadono al suolo, dato che le altezze raggiungibili dalle cose terrene sono ridicole rispetto al raggio r della Terra. Il peso diviso per la massa è quindi proprio g.

La massa è sempre la stessa, ovunque si vada nello Spazio, mentre il peso dipende dal corpo che ci attira verso di sé.

Per definire questa forza non c’è assolutamente bisogno che la Terra ruoti. La gravità esiste, comunque, insieme a tutta la sua bella ragnatela di accelerazione, che al suolo vale proprio g. Ripetiamo ancora:  un corpo che poggi sulla superficie di un pianeta (la Terra, ad esempio) è soggetto alla forza di gravità e alla sua accelerazione e quindi vorrebbe proseguire verso il baricentro del pianeta, ma ne è ostacolato dal terreno, una materia troppo dura per essere perforata. Il corpo spinge verso di lui e il terreno si ribella seguendo la terza legge della dinamica e ci fa sentire il peso che abbiamo. In realtà, il peso si sente proprio per la reazione che il terreno applica su di noi.

Immaginate una mela che ci cade in testa (tanto per non dimenticare il signor Newton). La mela ha un suo peso, ossia, una sua forza peso che è quella che l’attira verso il centro della Terra, regalandogli la famosa accelerazione di gravita che la fa cadere verso il basso. Se la nostra testa si frappone a questa caduta, agisce come il terreno agisce su di noi: ferma la caduta della mela. La forza peso della mela si trasferisce sulla nostra testa che “sente” il peso della mela  e dà luogo a un bel bernoccolo. Se la reazione della testa  (o del suolo) non è sufficiente a bloccare il movimento della mela, il suolo si deforma (si forma un buco, ad esempio) e/o la testa si rompe.

Con queste idee ben chiare, guardiamo cosa succede sul nostro pianeta. Immaginiamo che esso sia una sfera perfetta e che non ruoti. Qualsiasi abitante della Terra è soggetto alla stessa accelerazione di gravità. Per trovare il suo peso basta moltiplicare la massa per una costante tipica della Terra, l’accelerazione g. Se due corpi hanno la stessa massa hanno anche uguale peso, dovunque si trovino.

Mettiamo, adesso, in rotazione il pianeta e lo facciamo ruotare attorno a un asse che passa per il centro. Gli abitanti sono adesso soggetti a una rotazione che li trascina insieme al terreno. Conviene risolvere il problema relativamente alla persona che ruota. Sappiamo benissimo che, pur dovendo inserire una forza fittizia, il fenomeno rimane sempre lo stesso. Cosa succede alla persona P che si trova a una certa latitudine? Lui sente nettamente una forza centrifuga che lo spinge verso l’esterno. Noi sappiamo che è una “fittizia” reazione a una forza centripeta, ma sappiamo anche che essa è una forza reale per l’osservatore che ruota. Che cos’è che riesce a fare stare fermo la persona P? Ovviamente la reazione alla forza centrifuga che è una forza centripeta. Tuttavia, la forza centripeta che può agire è la gravità terrestre. Essa, però, è diretta verso il centro della sfera e non è perpendicolare all’asse di rotazione. Dobbiamo, allora, scomporre questa forza di gravità in due componenti: Una è quella centripeta che pareggia la forza centrifuga, l’altra è ciò che rimane della forza di gravità, ossia della forza peso della persona.

In Fig.19, basta fare il solito diagramma vettoriale e trovare la risultante di questa somma di forze. Una, quella centrifuga è diretta in direzione perpendicolare all’asse di rotazione, l’altra, quella di gravità è diretta verso il centro della Terra, Non ci resta che sommarle e troveremo ciò che resta della forza di gravità a cui è soggetta la persona P. Ricordiamoci, infatti, che una parte della forza peso è servita a compensare la forza centrifuga e fare sentire FERMA la persona P. La forza di gravità finale non è più diretta verso il centro della Terra ed è diminuita come modulo. Cosa succede all’equatore? Beh… la forza centrifuga è diretta in direzione opposta alla gravità. La forza peso si ottiene proprio togliendo al modulo della forza di gravita il modulo della forza centrifuga. Il peso è quindi minimo.

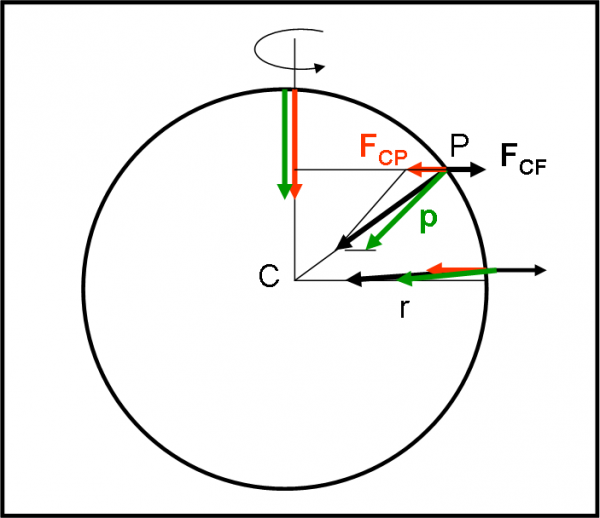
Dato che la massa è sempre la stessa, possiamo dire che a causa della rotazione la g non è più costante sulla Terra, dato che essa è proprio il rapporto tra forza peso e massa del corpo. E se la forza peso cambia, deve cambiare anche g, ricordando che:

p/m = g

Il peso di un corpo è massimo ai poli, dove la forza centrifuga è uguale a zero e quindi il peso è esattamente uguale alla forza di gravità, diretta proprio verso il centro della Terra.

Solo un cenno ulteriore al fatto che quanto abbiamo raccontato vale per un corpo perfettamente rigido. In realtà la Terra è composta soprattutto da acqua che può spostarsi, ossia non è vincolata al terreno. Capita, allora, che una goccia d’acqua a grandi latitudini tende a essere spostata verso l’equatore. Abbiamo infatti visto che la direzione della forza di gravità NON è perpendicolare alla tangente alla sfera terrestre nel punto P. Ciò vuol dire che esiste una componente che applica un’accelerazione diretta verso il basso e trascina la goccia con sé (la goccia può scorrere sulle altre, essendo un liquido). In poche parole, le gocce tendono a concentrarsi verso l’equatore dove si devono fermare perché in quel punto sparisce la componente della gravità che non è perpendicolare alla tangente. Ai poli la Terra si schiaccia e all’equatore si gonfia. Chi ha giocato questo scherzetto? Nuovamente la forza centrifuga che ha comandato la variazione della direzione della forza di gravità risultante e ha fatto subire un’accelerazione diretta verso l’equatore (freccia azzurra). La situazione è riassunta nella Fig. 20.

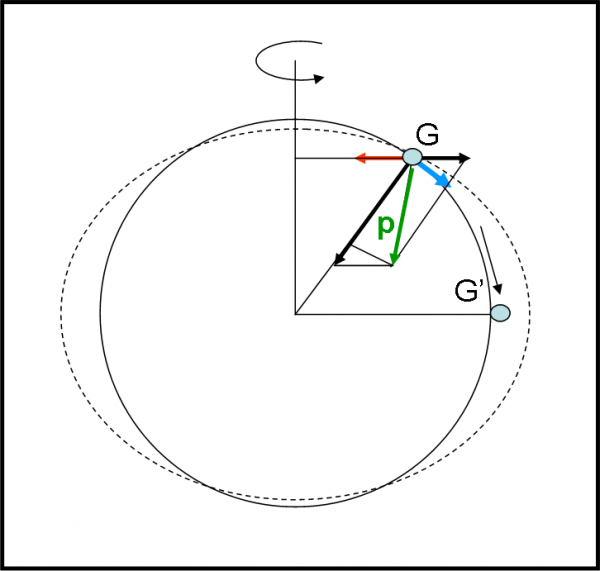
Se non avete capito bene come si può scorrere verso il basso, pensate a una discesa asciutta e a una discesa ghiacciata. Nel primo caso, se qualcuno vi spinge leggermente verso il basso riuscite, comunque, a stare fermo; nel secondo caso, invece, scivolate senza speranza,  Siete, in pratica, svincolati dal terreno. Qualcosa di simile a quanto abbiamo visto con l’automobile sul ghiaccio… Questa forma ellittica della Terra gioca ulteriormente sul peso di un corpo, dato che la gravità cambia anche a causa della variazione del raggio r della Terra che è massimo all’equatore e minimo ai poli.

Non voglio girare il coltello nella piaga… ma una goccia che scivola su una superficie rotante è soggetta anche a un’altra forza “fittizia”, quella di Coriolis, come già accennato prima. Vi faccio un ultimo esempio su Coriolis. Immaginate di essere su un autobus. Come già visto, quando è in curva sentite la forza centrifuga che vi spinge verso il finestrino. Provate, adesso, a muovervi lungo il corridoio. State facendo come la pallina da golf sulla piattaforma rotante. Non sarà facile camminare perché alla forza centrifuga si aggiunge anche quella di Coriolis… Insomma, voglio proprio farvi venire voglia di acquistare il libro…. ah ah ah… Tra parentesi, dopo le lezioni sulla matematica non dovreste più vere paura delle formule…

Va bene. Abbiamo concluso la nostra lunga disquisizione sulla caduta della Luna che ci ha portato ben più lontani. La risposta più giusta alla domanda di partenza è allora: “Sì, la Luna continua a cadere verso la Terra, ma la sua inerzia, ossia la sua velocità che cerca di mantenerla un moto rettilineo uniforme, ritarda indefinitamente il momento della caduta”. Vale , però, anche l’altra risposta: “No, la Luna se se ne sta andando per la sua strada, ma è attirata istante per istante verso la Terra e riesce a non scappare e a girare indefinitamente intorno al pianeta”. Insomma, avete capito il succo dell’intero discorso? Ciò che conta nella descrizione è solo e soltanto il sistema di riferimento. La Luna non fa altro che seguire lo stesso identico fenomeno: un moto circolare uniforme attorno alla Terra. A questo punto, il suo moto si potrà anche spiegare, e discutere, attraverso altre grandezze fisiche, come il momento angolare e l’energia…