L'articolo sull'aberrazione relativistica, spiegata in modo molto semplicistico, mi ha fatto pensare a una rappresentazione più generale che descriva sia la stessa aberrazione, ma anche il redshift relativistico e, per finire, la dilatazione del tempo. Insomma, un disegno a quattro dimensioni che rappresenti abbastanza bene cosa si vede quando si viaggia a una velocità v comparabile con la velocità della luce. Un esercizio semplice che necessita solo ricordare il famoso fattore di Lorentz che già avevamo introdotto QUI. Ricordiamo solo che questo fattore, ricavato in modo geometricamente banale, è la quantità che permette di calcolare sia la dilatazione del tempo che la contrazione delle lunghezze nella teoria della relatività. E dico poco!

A questo punto potrei costruire subito lo spazio a quattro dimensioni relativo a un viaggiatore spaziale in rapido movimentato. Preferisco, però, farvi prima vedere come si riesce ad arrivare a una rappresentazione che penso sia estremamente istruttiva per molte applicazioni. Ed è anche una delle poche che, senza bisogno di metriche speciali e di formule complesse, riesce a dare tutte le informazioni sullo spaziotempo e calcolare direttamente tutti i parametri ad esso relativi.

Iniziamo, allora, riprendendo il concetto di aberrazione relativistica affrontata pochi giorni fa e vediamola sotto un diverso punto di vista. In quell’articolo abbiamo fatto muovere la stella e abbiamo visto come il movimento influenzi la luce che giunge sulla Terra. Il sistema di riferimento è quello terrestre e si considera fermo il nostro pianeta. Si è, però, accennato a come il cielo sembrerebbe restringersi andando a grandi velocità. Bene. Partiamo proprio da lì, più o meno.

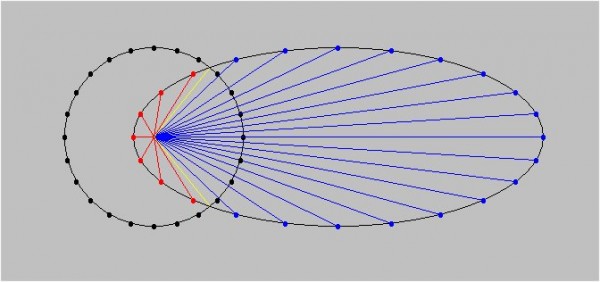
Consideriamo, in Fig. 1, la nostra astronave A immobile in un certo punto dell’Universo.

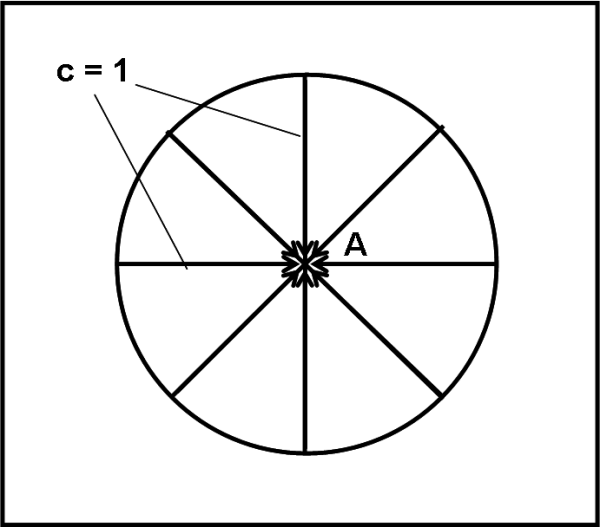
Verso di lei piovono i fotoni provenienti da ogni parte della sfera celeste. Fatemene considerare solo otto, ma più che sufficienti per comprendere la situazione. La circonferenza attorno all’astronave A è relativa a un attimo prima che i fotoni la colpiscano e consideriamo il suo raggio proprio uguale alla velocità c della luce, o meglio allo spazio relativo a un secondo prima dell’arrivo. In tali condizioni lo spazio diviso il tempo, che è uguale a uno, è proprio la velocità. I vettori che hanno lunghezza uguale al raggio della circonferenza hanno quindi come modulo (ossia valore assoluto) proprio c.

Fin qui direi che non ci sono problemi. E’ quello che capita a un osservatore che guarda il cielo attorno a lui. In ogni momento arrivano i fotoni delle stelle ed essi giungono da ogni direzione con velocità uguale a c. Pensateci prima di mettere l’occhio nel telescopio o nel binocolo di ultima generazione. In ogni momento siete soggetti a una pioggia continua di fotoni che arrivano da ogni direzione e che vi colpiscono tutti assieme, proprio come se stesse piovendo luce. Piovendo… ho detto piovendo. Proprio la pioggia ci era servita  per spiegare l’aberrazione annua… Tenetelo ben presente, può aiutare molto.

E’ il momento di mettere in moto la nostra astronave. Immaginiamo di raggiungere immediatamente una velocità di crociera v abbastanza elevata, pari a 0.6 volte quella della luce. Non è male, anche se si può fare di meglio. Non ho considerato una velocità proprio uguale a c, dato che il disegno diverrebbe meno intuitivo e più difficile da rappresentare. Tuttavia, una volta compreso il meccanismo, lo potete fare da soli o almeno comprendere come si deformerebbe.

L’astronave viaggia verso destra. Il che vuol dite che i fotoni che giungono verso di lei sono anche soggetti a una velocità uguale e contraria (ossia a una – v, diretta verso sinistra) disegnata come segmento azzurro. E’ esattamente ciò che capitava con l’aberrazione “normale”, quando combinavamo la caduta della pioggia con la nostra corsa per metterci al riparo.  Costruiamo allora, in Fig. 2, la somma vettoriale delle velocità per ognuno degli otto fotoni che stanno raggiungendo l’astronave.

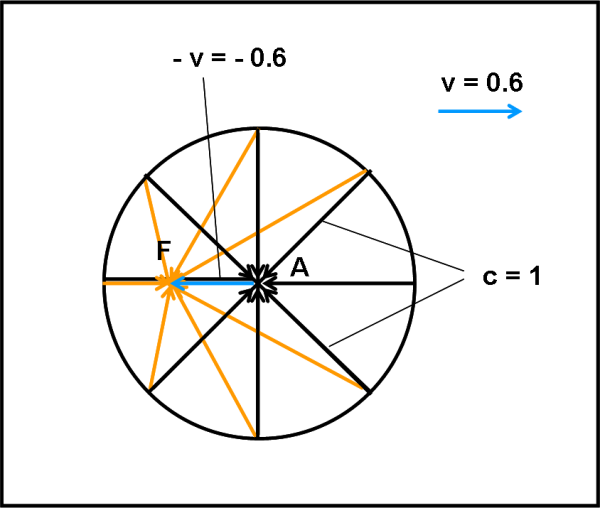
Ovviamente essi cambiano direzione apparente e i vettori risultanti sono rappresentati dai segmenti arancioni. Quello che è veramente interessante è, però, che i fotoni si dirigono tutti verso uno stesso punto, che ovviamente non coincide più con l’astronave (anche nell’aberrazione annua il telescopio doveva essere puntato verso una direzione diversa da quella teorica). Non era comunque difficile prevederlo da come si è costruita la somma di vettori…

Prima di proseguire, fatemi richiamare un punto essenziale. Tutto ciò che stiamo per fare è relativo al sistema di riferimento dell’astronave in movimento (non per niente la teoria si chiama della relatività). Se cambiassi astronave cambierebbe il risultato. In altre parole, non è l’Universo che cambia, ma solo ciò che vede l’astronave. O, ancora, le lunghezze e i tempi cambiano perché ci riferiamo a un oggetto in movimento. Un oggetto fermo vedrebbe le cose in modo ben diverso.

Il punto F è il punto di raccolta degli otto fotoni. Ciò che vede realmente l’astronave è la situazione relativa proprio a questo punto F. In realtà, potrei tracciare dal punto A le parallele alle linee che convergono in F e mi accorgerei dell’effetto dell’aberrazione in quanto le linee si concentrerebbero verso la direzione del movimento, in modo analogo a quanto fatto nell’articolo sul pianeta appena scoperto. Tuttavia, avrei una rappresentazione corretta della situazione apparente, ma la limiterei solo all’effetto di aberrazione. Molto meglio deformare la Fig.2 in modo da visualizzare tutto insieme lo spaziotempo e gli effetti dovuti alla velocità dell’astronave.

A questo punto entra in scena il fattore di Lorentz che già conoscete. Esso, se ricordate bene, permette di calcolare la dilatazione del tempo e la contrazione delle lunghezze per un sistema di riferimento in moto con una velocità comparabile a quella della luce. Dovete, però, credermi sulla parola. L’esatta motivazione della deformazione che sto per fare può essere spiegata analiticamente attraverso le formule. Ma noi non le vogliamo e allora vediamo solo quali sono i risultati pratici della trasformazione che introduce il fattore di Lorentz.

Cosa dobbiamo fare praticamente? Non molto. Innanzitutto considerare il punto F come il fuoco di un ellisse che abbia il semiasse minore uguale al raggio della circonferenza iniziale. Questo vincolo si può capire abbastanza bene, pensando che la direzione perpendicolare alla direzione del moto dell’astronave deve essere in qualche modo non soggetta a particolari deformazioni. Ma capiremo meglio la situazione, applicano la trasformazione fondamentale.

Dobbiamo, adesso, “stirare” il cerchio originario fino a farlo diventare un’ellisse di cui F è il fuoco. Il fattore di “stiramento” è proprio il fattore di Lorentz γ. In parole più tecniche, il semiasse maggiore dell’ellisse deve essere proprio il fattore di Lorentz, considerando uguale a 1 il raggio della circonferenza (ossia la velocità della luce è posta uguale a 1 e γ viene espresso in funzione di questa scelta semplificativa).

Quanto vale questa dilatazione? Basta ricordare la formula che descrive il fattore di Lorentz (che avevamo ricavato in modo semplicissimo) e inserire al posto di v e c i valori attuali, ossia c = 1 e v = 0.6. Per la proprietà dell’ellisse la distanza del fuoco F dal centro dell’ellisse C è dato da vγ. Ai più preparati non è sfuggito il fatto che la distanza tra fuoco e centro di un’ellisse è il prodotto tra il semiasse maggiore e l’eccentricità. Dato che γ è proprio il semiasse maggiore della nostra ellisse ne segue che la velocità v dell’astronave è l’eccentricità. D’altra parte se essa tende a zero, C coincide con F e torniamo alla circonferenza iniziale. Se, invece v aumenta può arrivare al massimo a 1, ossia a c (che abbiamo posto uguale a 1). L’ellisse diventa una parabola che definisce le condizioni estreme della deformazione dello spazio tempo. Non complichiamoci le cose (chi se la sente può proseguire tranquillamente) e torniamo alla nostra velocità di 0.6. Il fattore di Lorentz è facilmente calcolabile, ricordando la formula che lo definisce:

γ = 1/(1- v2/c²)^1/2 = 1/(1 – 0.6²/1)^1/2 = 1.25

Notate che se v = c, γ è ∞ e quindi l’ellisse non si chiude, diventando una parabola.

La Fig. 3 ci mostra l’ellisse finale, che ci permette di leggere tutti i più importanti parametri che definiscono lo spaziotempo relativo all’astronave in movimento.

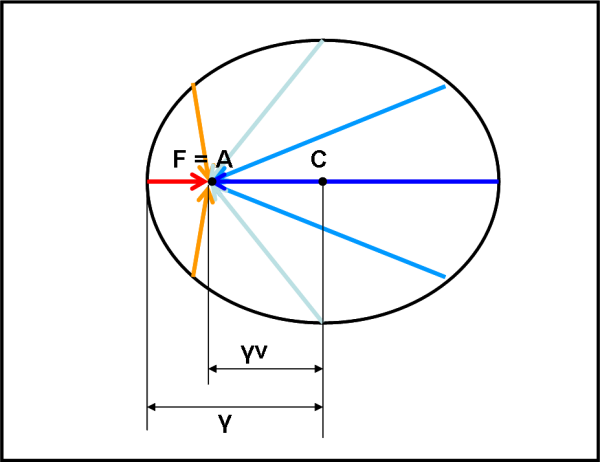
Vediamoli uno per uno e cerchiamo di capire quanto sono stati geniali i signori Einstein e Lorentz. Il tutto diventa semplicissimo e ovvio, anche se per arrivarci, passo dopo passo, bisognerebbe entrare in una matematica non certo banale. Noi possiamo gustarci il risultato finale e la sua geniale semplicità o -se preferire- semplice genialità.

Innanzitutto, notiamo benissimo che la situazione che appare all’astronave A è aberrata relativisticamente, ossia lo spazio si concentra davanti a lei e si allarga dietro. Lo stesso fenomeno che avevamo visto per il “pianeta Einstein”. Tuttavia, nell’ellisse possiamo proprio calcolare i valori corretti delle deformazioni. Le lunghezze delle linee dei fotoni che raggiungono l’astronave a partire dall’ellisse rappresentano esattamente l’energia che posseggono, o -meglio ancora- la frequenza (e quindi la lunghezza d’onda). E’ immediato colorare le linee del colore corrispondente: davanti all’astronave i segmenti sono più lunghi e quindi è maggiore la frequenza e minore la lunghezza d’onda. In parole povere, siamo nel blu (e oltre) e assistiamo al fenomeno del blueshift relativistico, dovuto al fatto che gli oggetti di fronte all’astronave si avvicinano a lei a grande velocità. Dietro all’astronave i segmenti s’accorciano e quindi aumentano le lunghezze d’onda e si va verso il rosso e oltre. E’ il redshift relativistico dovuto alla grande velocità di allontanamento degli oggetti posti alle “spalle” dell’astronave.  Notate che lungo l’ellisse vi saranno due punti in cui la lunghezza del segmento che unisce ellisse e fuoco è uguale al raggio della circonferenza di Fig. 1. E’ l’unica direzione in cui la luce non subisce spostamento di lunghezza d’onda e mantiene le condizioni iniziali. E’ lì che bisogna guardare se non si vuole essere travolti dagli effetti spaziotemporali!

Ho detto “temporali”? Sì, esattamente. Le lunghezze dei segmenti indicano anche quanto il tempo si dilati o si accorci nelle varie direzioni. D’altra parte il fattore di Lorentz è come il “prezzemolo” e (ricordate?) ci permette proprio di stabilire la dilatazione del tempo per un viaggiatore spaziale.

Insomma, muniti di un righello e di un goniometro da poco prezzo (e niente di più), siamo in grado di misurare direttamente l’energia dei fotoni, la loro frequenza, la dilatazione del tempo e delle lunghezze legata all’angolo di deformazione sotto cui l’astronave vede lo spazio attorno a lei. Siamo anche in grado, perciò, di disegnare la deformazione di una qualsiasi figura sia posta in un certo punto dello spazio.

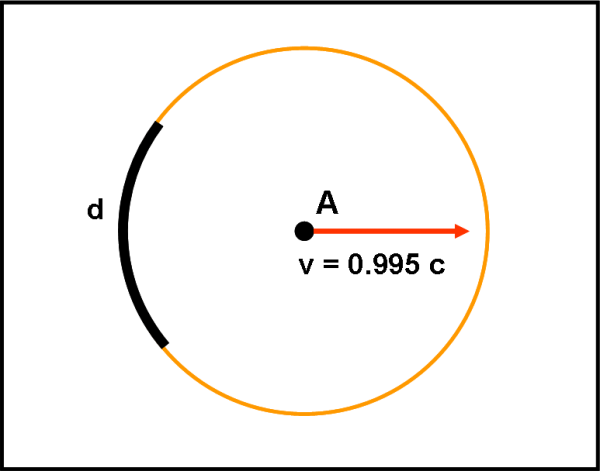
Poniamo, ad esempio, un bel “disegno” dietro l’astronave (è il posto migliore per vedere effetti veramente speciali…) e deformarlo secondo quanto descritto prima.

Basta seguire le lunghezze dei segmenti fuoco-ellisse a partire dalle condizioni iniziale in cui il disegno era posizionato sulla circonferenza ad astronave ferma, come mostrato in Fig. 4, dove il disegno è d.

Dato che stiamo parlando di risultati di geni della fisica, voglio proporvi un esempio basato su un capolavoro di un altro genio: Leonardo da Vinci. Anch’egli amava e capiva la Natura come forse nessuno è mai riuscito a fare. Mi sembra quindi ovvio usare un suo celebre dipinto. Sono riuscito a scovare la deformazione subita dall’Adorazione dei Magi (il disegno fantastico di preparazione al quadro, Fig. 5) sia vista proprio nella direzione del movimento dell’astronave sia nel piano dell’ellisse di Fig. 3. Le Fig. 6 e 7 ci regalano le due rappresentazioni. Come vedete il disegno è posto DIETRO l’astronave, ma, per il fenomeno dell’aberrazione, si vede benissimo anche davanti e, magicamente, si colora da solo. La deformazione è relativa a una velocità veramente prossima a quella della luce, ossia v = 0.995.

Chi ha voglia di pensare, troverà un sacco di similitudini tra la traiettoria orbitale di un corpo celeste  e la variazione della luce dei fotoni visti dall’astronave in movimento. Troverà la legge delle aree che si lega perfettamente alla variazione causata dall’effetto Doppler e alla dilatazione delle lunghezze e del tempo. E molte altre cose. Insomma, un articolo che può essere solo un punto di partenza per viaggi sempre più avventurosi. Ad esempio, non stupitevi se avessimo davanti il Sole e partissimo verso di lui accelerando fino a raggiungere la velocità della luce: all’inizio sembrerebbe allontanarsi, dato che tutti i raggi luminosi si concentrerebbero verso la direzione del moto e vedremmo la nostra stella rimpicciolire e sempre più oggetti davanti a noi (un po’ come abbiamo visto succedere per Orione nell’articolo sul pianeta Einstein).

Prima di concludere, vorrei ancora ribadire che la Fig. 3 è una perfetta rappresentazione delle quattro dimensioni e siamo riusciti a disegnarla sul piano di un foglio. Si potrebbe facilmente anche portarla nelle tre dimensioni spaziali, utilizzando un ellissoide a due assi (a > b = c). In ogni modo, essa descrive completamente le variazioni di tutte e quattro le dimensioni dello spaziotempo. Possiamo quindi consideralo un vero e proprio disegno a quattro dimensioni, dove, se qualcuno volesse, potrebbe anche divertirsi a inserire masse aggiuntive e vedere le deformazioni spaziotemporali dovute a queste intruse. Per il sito, però, è meglio fermarci qui…