Vorrei cominciare con un appello. Vi prego fortemente di leggere e seguire questa serie di articoli, non solo sono molto semplici e divertenti, ma fondamentali per delineare nel modo migliore la MQ e le sue conquiste. Qualsiasi estrapolazione ai confini della conoscenza, deve  poggiare saldamente i piedi sulla QED.

L’elettrodinamica quantistica (QED) studia sostanzialmente le interazioni tra gli elettroni e il campo elettromagnetico. Essi interagiscono tramite lo scambio di fotoni e di varie particelle virtuali, proprio quelle che nascono attraverso le fluttuazioni quantistiche. In parole più semplici e generali, la QED è la teoria più completa ed esauriente delle interazioni tra luce e materia. Lo scopo di questa serie di articoli è proprio quello di cercare di descriverla con le parole e i diagrammi più semplici possibili. Spesso definita come “gioiello della fisica”, essa riesce a spiegare una serie infinita di fenomeni e può essere considerata una delle teorie più esatte anche se rimane … incomprensibile.

Inizio questo arduo compito ringraziando colui che ha permesso, anche al mio modesto cervello, di riuscire a capire l’armoniosa semplicità che domina questo argomento, fondamentale per entrare completamente nel mondo della MQ. Mi riferisco, ovviamente a Richard Feynman e al suo corso di lezioni sull’elettrodinamica quantistica. Ringrazio, inoltre, tutti voi che cercherete di seguire il mio umile tentativo di imitare tale maestro. In ogni modo, sappiate che se risulterò comprensibile il merito è solo e soltanto del grande Richard.

Prima di prendere per mano un fotone e seguirlo nella sua vita così avventurosa e, spesso, inaspettata, fatemi sintetizzare un concetto che Feynman amava ripetere spesso e che io ho fatto mio (come spesso leggete nelle mie esternazioni). La maggior parte delle persone si interessa e vuole conoscere le ultime novità, relative ad argomenti che ancora non si conoscono. Poche volte si limita a cercare di sapere quello che si conosce con sufficiente sicurezza. Feynman diceva che la gente preferisce mangiare un cibo mezzo-cotto piuttosto che gustare manicaretti preparati a regola d’arte. Bene, l’elettrodinamica quantistica (QED) è un arrosto cotto al punto giusto, eppure è quasi sconosciuta ai più, che preferiscono cibarsi di teorie aleatorie ancora ben lontane dalla giusta cottura. Vi assicuro che parlare di una cosa ben stabilita come la QED è tutto fuorché noioso e/o difficile e riserva sorprese impreviste.

Il succo di tutto questo ramo della MQ è descrivere i rapporti tra la luce e la materia. Il che può ancora essere sintetizzato nelle interazioni tra fotone ed elettrone. In realtà, questo incontro è il primo e fondamentale abbraccio che avviene tra luce e materia. La QED non si ferma all’esterno del nucleo atomico, ma ha tutte le potenzialità per entravi dentro ed essere applicata a una folla di “particelle” ben diverse dagli elettroni, siano essi quark o gluoni. L’importante è seguire lo stesso "stile" quantico. A noi, comunque, basterà limitarci alla periferia atomica: c’è già abbastanza carne al fuoco e -soprattutto- ben cotta!

Non è male ricordare un altro requisito fondamentale necessario per seguire questi articoli. Un requisito evidenziato perfettamente da Feynman: l’importante è accettare di non capire cosa si sta studiando. Sembra un’assurdità, che però non è più tale entrando nella MQ. Quando Feynman iniziava a spiegare i concetti dell’elettrodinamica quantistica, di cui è stato il vero maestro sia scientifico che divulgativo, diceva chiaramente al suo pubblico che non avrebbe capito assolutamente cosa gli avrebbe spiegato. In effetti, erano le stesse cose che insegnava all’Università. Tuttavia, non vi erano problemi di preparazione e di istruzione, dato che i suoi studenti, per primi, non riuscivano a capire le sue spiegazioni. Erano quindi in buona compagnia. Ai volti dubbiosi e stupiti dell’uditorio, se non peggio, il grande scienziato aggiungeva subito che la ragione di quella incomprensione era una e una sola: lui stesso non capiva niente di quell’argomento!

Come già sappiamo, le motivazioni di questo discorso un po’ insensato sono insite nella MQ. Essa descrive la Natura in un modo del tutto estraneo al senso comune della logica e della razionalità. La meraviglia è che tutti gli esperimenti la confermano. Ne segue che se si vuole accettare la Natura bisogna anche accettare la sua assurdità. Il non capire qualcosa è il primo passo per la conoscenza delle leggi quantistiche che governano l’Universo.

Una strana particella

Vi sembrerà sciocco o inutile, tuttavia fatemi definire cosa intendiamo per fotone. Esso è una particella che trasporta l’informazione luminosa. A ognuna di loro è associata una “nota” o se preferite un codice numerico, che può essere grande o piccolo e che viene chiamato frequenza o colore. Sappiamo bene che per parlare di frequenza bisognerebbe considerare la luce come un’onda, ma per i nostri scopi possiamo benissimo limitarci ad associare a ogni  "tipo" di fotone  un certo numero (frequenza o colore) che lo caratterizzi.

Questo codice o nota si può sentire ogni qual volta un fotone colpisce un rivelatore. Il “tac” corrispondente sarà più o meno "forte" a seconda del codice del fotone. Ricordiamo anche che se un fotone colpisce un rivelatore non può colpirne anche un altro. In poche parole, non possiamo dividere il fotone in modo che metà colpisca un rivelatore e un’altra metà ne colpisca un altro. O tutto o niente. Il fotone è una particella indivisibile.

La luce (e quindi i fotoni) causa un numero incredibile di fenomeni che fanno parte del mondo “normale” e razionale. La luce si scompone in colori; si muove lungo una retta; si piega quando entra nell’acqua; si riflette quando colpisce uno specchio e l’angolo che la retta di arrivo fa con la perpendicolare al piano dello specchio è uguale a quello fatto tra quest’ultima e quella della luce riflessa; una lente concentra la luce; ecc., ecc.

Ebbene, tutti questi fenomeni “logici” e “comuni”, possono essere descritti,  in modo assurdo e non comprensibile, con la MQ, in particolare con l'elettrodinamica quantistica.

Riflettere o non riflettere, questo è il problema

Dedichiamoci a un fenomeno che ha ispirato molti pittori e che ha sempre affascinato le persone più romantiche: la riflessione parziale della luce da parte del mare o di un lago. Se si guarda all’interno dell’acqua si vede ciò che sta sotto la superficie (la luce deve quindi penetrare), ma, nello stesso momento, si vede anche il riflesso di qualche cosa che illumina la superficie (la Luna o il vostro volto o lo stesso Sole). Si può quindi facilmente concludere che parte della luce viene riflessa e parte viene rifratta, ossia penetra nell’acqua, anche se con un percorso "piegato" rispetto a quello con il quale l’aveva colpita.

La stessa cosa capita se accendete una lampada in casa in pieno giorno e guardate il vetro della finestra: vedreste sia ciò che sta succedendo all’esterno, ma anche il riflesso della lampada. Un’ulteriore prova che la luce è capace sia di attraversare il vetro sia di essere riflessa. Questo è un fenomeno che si può facilmente descrivere con l’ottica geometrica e con la fisica classica. Tuttavia, ben più generale (e assurda) è la spiegazione che si può dare attraverso la QED.

Innanzitutto, facciamo una semplificazione, che correggeremo più tardi: assumiamo che la riflessione sia dovuta solo alla superficie dell’acqua o del vetro. In realtà, dovremmo già iniziare a pensare che un pezzo di vetro è un sistema estremamente complesso, in cui una quantità incredibile di elettroni si agitano continuamente. Se vogliamo entrare nel mondo della QED, un pezzo di materia deve essere considerato in questo modo. Quando un fotone entra nel vetro interagisce con gli elettroni e compie una specie di frenetica danza. Tuttavia, il risultato finale è del tutto simile a quello che si ottiene considerando solo ciò che capita sulla superficie. Lo vedremo meglio successivamente.

A questo punto siamo pronti a fare un esperimento ideato da Feynman. Ciò che ci occorre è un pezzo di vetro, due rivelatori di fotoni e qualche fotone con lo stesso codice, ossia con la stessa frequenza o colore. Un rivelatore R1 aspetta i fotoni che rimbalzano indietro e l’altro, R2, viene “inserito” dentro al vetro in modo da catturare quelli che entrano. L’esperimento è rappresentato in Fig. 1.

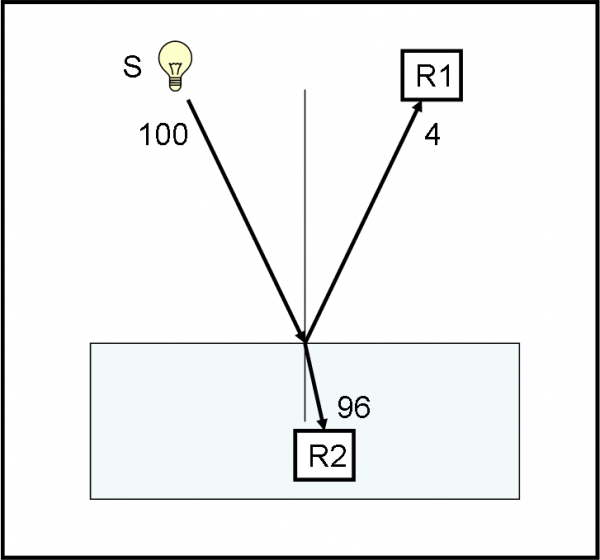
Lanciamo 100 fotoni dalla sorgente S. Poi andiamo a controllare cosa hanno ricevuto i due rivelatori R1 e R2. Il primo solo 4 e il secondo 96. Possiamo facilmente concludere che 96 fotoni sono penetrati nel vetro e 4 sono stati riflessi. Niente di speciale? Ebbene no. Già questo risultato, dall’apparenza ovvia per quanto sappiamo dall’esperienza di tutti i giorni, impone una domanda imbarazzante: “Come fa un fotone a scegliere se andare in R1 o in R2?” Sembrerebbe una domanda assurda, che non merita una risposta. Ma, riflettendoci sopra, è invece essenziale e molto seria. Potremmo riformularla più correttamente: “Perché qualche fotone (4) finisce in R1 e molti altri (96) finiscono in R2?”. I fotoni sono per definizione perfettamente uguali e hanno anche lo stesso numero che li identifica (la stessa frequenza). Non ha alcun senso che si comportino in maniera diversa. La QED va a nozze. La domanda è assurda? Perfetto. Si può tranquillamente dare una risposta altrettanto assurda, ma attraverso una teoria ineccepibile. Iniziamo il grande gioco della MQ e seguiamo Alice, ops… i fotoni!

Prima, però, cerchiamo con un ultimo tentativo disperato di azzardare qualche altra teoria che rimetta le cose su un piano normale. La domanda è assurda, ma la risposta potrebbe rimetterla nel senso comune. Ad esempio, potremmo pensare che il vetro è formato, per la maggior parte, da buchi (il 96%) che permettono alla luce di infilarsi all’interno. Solo il 4% è solido ed è quello che riflette qualche fotone. La teoria è facilmente distruttibile, soprattutto dopo aver pulito e levigato perfettamente la superficie del vetro. Niente cambia e i fotoni continuano a comportarsi in modo diverso. No, la faccenda non può risolversi con una strana struttura del vetro. Se la colpa non è del vetro, può darsi che sia dei fotoni. Loro sembrano identici e invece hanno una qualche caratteristica intrinseca diversa. Come fare a provarlo? Facile: basta inserire prima del blocco di vetro, alcuni “filtri” anch’essi formati da superfici riflettenti. Se un fotone è del tipo “che passa”, quelli che arrivano sulla nostra superficie devono essere solo quelli che riescono a entrare. E, invece, capita tutto esattamente come prima. Di 100 fotoni che arrivano, 96 fotoni attraversano il pezzo di vetro, ma 4 continuano a essere riflessi.

La scelta del fotone

Non ci rimane che entrare nel mondo dell’assurdo e dire che è impossibile conoscere cosa decide di fare il singolo fotone. Può “scegliere” di andare dritto o rimbalzare, ma è una decisione tutta sua che non potremmo mai conoscere. Tuttavia, qualcosa può essere conosciuto, ossia la percentuale di fotoni che tornano indietro rispetto a quelli che avanzano. Non possiamo prevedere quale fotone fa una scelta o l’altra, però possiamo dire che il 4% torna indietro e il 96% va avanti. Vi rendete conto di quello che abbiamo detto? La fisica, quella scienza che descrive e spiega in modo esatto, è costretta a calcolare soltanto la probabilità di un evento. In altre parole, ancora più pesanti, la Natura ci permette solo di calcolare una probabilità. Assurdo, veramente assurdo!

Tuttavia, questo risultato è ancora niente rispetto a quello che ci attende, complicando un poco l’esperimento. Al posto di una sola superficie riflettente, ne prendiamo due. Ciò si ottiene con una lastra di spessore molto piccolo in cui la superficie superiore e quella inferiore siano perfettamente parallele.

Sappiamo già molto bene che alcuni fotoni si riflettono sulla superficie d’entrata, ma altri possono riflettersi su quella di uscita (ricordiamoci che, per il momento, abbiamo considerato  che la riflessione avvenga solo su una superficie). Poniamo il rivelatore R2 al di sotto della lastra sottile, come rappresentato in Fig. 2. Facciamo un po’ di conti, accettando l’assurdità che i fotoni possano scegliere e che noi ci si possa limitare solo a un calcolo delle probabilità. Dunque, la prima superficie rifletterebbe solo 4 fotoni e 96 dovrebbero passare (ne abbiamo avuto conferma diretta). I 96 che entrano colpiscono la seconda superficie e dovrebbero subire lo stesso fenomeno. Il 4% dei 96 dovrebbe nuovamente essere riflesso. Senza voler andare troppo nel sottile, i fotoni o sono uno o zero e non frazioni dell’unità: ci dobbiamo aspettare che sul rivelatore R1 arrivino o 7 o 8 fotoni dei 100 inviati.

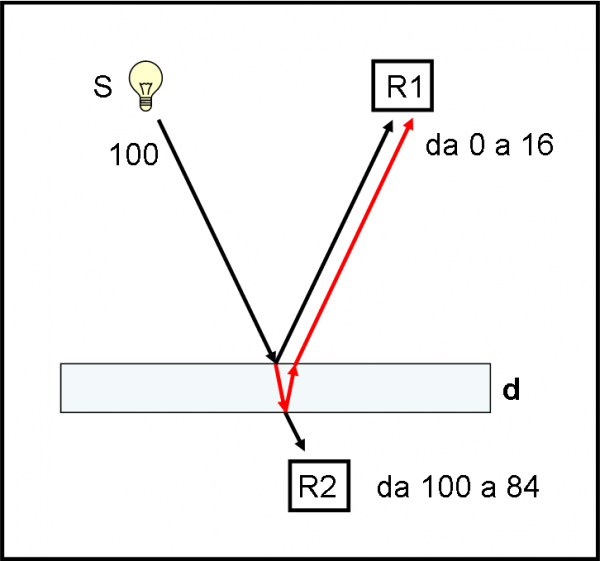
Già in questo modo abbiamo dovuto fare uno sforzo di illogicità, accettando di ragionare solo in termini di probabilità di fronte a un fenomeno fisico che la Scienza dovrebbe poter spiegare e calcolare perfettamente. No, non saltate sulla sedia, c’era da aspettarselo: i fotoni ricevuti da R1 sono molti di più, ben 16! Ciò è ulteriormente confermato dal fatto che R2 ne riceve solo e soltanto 84. Non si può nemmeno sperare che i fotoni si siano, in qualche modo, moltiplicati. Vi rendete conto che stiamo azzardando sempre più risposte fuori dalla logica comune? Bene, bene… vuol dire che stiamo seguendo Alice.

Tuttavia, quel 16% ci mette veramente in crisi, pur con tutti gli sforzi che stiamo facendo. Non solo dobbiamo continuare a parlare in termini di probabilità, ma dobbiamo anche accettare il fatto che la seconda superficie sembra amplificare l’attesa probabilistica.

Non basta ancora, però. Proviamo a cambiare la lastra di vetro con delle altre del tutto simili come materiale. I numeri sembrano prenderci in giro. A volte in R1 arrivano solo 1 o 2 fotoni in totale. Altre volte non ne arriva nessuno. Mamma mia, non ci capiamo più niente! Cerchiamo di ragionare e di dare  regolarità ai nostri esperimenti. Sì, in effetti, qualcosa è cambiato da una volta all’altra. Anche se di pochissimo, lo spessore della lastra è variata. Possiamo tentare di concludere che il numero di fotoni riflessi dalle due superfici dipende essenzialmente dalla loro separazione. Piano, piano... va bene accettare tutto, ma cerchiamo di fare un po’ di ordine ed eseguire ulteriori esperimenti mirati allo scopo.

Cominciamo con una lastra sottilissima, il cui spessore possa considerarsi praticamente zero. R1 riceve mediamente soltanto 1 fotone. Aumentando lo spessore, appena appena, ci sentiamo un po’ meglio: R1 riesce a ricevere proprio 8 fotoni, il numero che ci saremmo aspettati all’inizio. La speranza è di breve durata. Se inseriamo una lastra più spessa, dell’ordine di 10^-7 metri, ossia 10^-4 millimetri, o, ancora, un decimo di micron (chiamiamola spessa!), il risultato torna a sbigottirci e i fotoni tornano a essere 16. Un valore massimo però. Aumentando ancora lo spessore il numero inizia a decrescere per tornare nuovamente a 1 o addirittura a zero. Continuando ad allargare la lastra, si ripete il ciclo e via dicendo. Insomma, lo spessore della lastra cambia la probabilità di avere un certo numero di fotoni riflessi e lo fa in modo perfettamente periodico. Anche la probabilità comincia a farci vedere cose assurde.

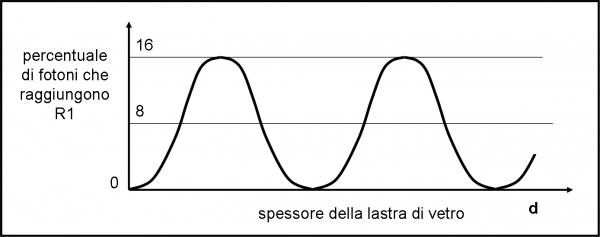
Possiamo, però, cercare di estrarre una qualcosa di comprensibile o -meglio- di logico in questo fenomeno: andando da un valore minimo a un valore massimo dei fotoni riflessi, il valore medio è proprio quel numero 8 che sarebbe stato plausibile per un ragionamento normale. Beh… è già qualcosa. Tuttavia, il valore 8 si ottiene , in realtà, solo due volte per ogni ciclo, quando lo spessore raggiunge un ben determinato valore o un suo multiplo esatto.

Feynman dice, giustamente, che si comporta come un orologio, dato che le lancette segnano una certa ora solo due volte in 24 ore. Questo risultato ha un certo senso matematico e può essere rappresentato attraverso la Fig. 3, dove in ascissa mettiamo lo spessore della lastra di vetro e in ordinata la percentuale di fotoni  che raggiungono R1. Come, ormai, ci aspettavamo, data la periodicità del risultato, la curva è una sinusoide, composta da una serie ininterrotta di massimi e minimi (vedete come serve lo studio delle funzioni?).

Decidere dopo... ciò che si sta facendo prima

Restiamo però con i piedi per terra (finché ci riusciamo). Stiamo accettando come logico e matematico un qualcosa che è di per sé un fenomeno completamente assurdo. Il numero di fotoni riflessi dovrebbe dipendere dalle caratteristiche intrinseche dei fotoni o, al più, dalla composizione del vetro. Il fatto che, aumentando o diminuendo la distanza tra le superfici parzialmente riflettenti, cambi la capacità delle stesse superfici di riflettere i fotoni, resta una vera assurdità nella logica comune. Ma la cosa è ancora più assurda. La seconda superficie riesce ad annullare ciò che dovrebbe comunque succedere nella prima.

Infatti, se accettiamo che la prima ne rifletta sempre il 4%, l’aggiunta della seconda superficie, qualsiasi sia la distanza dalla prima, potrebbe aumentare oppure no il numero dei fotoni riflessi (e già questo è alquanto strano), ma non certo riuscire ad annullare quelli della prima. Sembrerebbe che i fotoni della prima riflessione non solo scelgano dove andare, ma decidano in base a ciò che capiterà ai loro fratelli nella seconda riflessione. In altre parole, ciò che capita nella seconda superficie sembra influire su ciò che capita nella prima, anche se avviene dopo. Questo fatto è veramente all’altezza del mondo di Alice e scombussola tutte le nostre convinzioni scientifiche di causalità e di freccia del tempo. Pensiamoci bene e ci troveremo veramente molto frastornati.

E’ il momento di inserire il coltello nella piaga ancora più a fondo. Come? Basta aggiungere una terza superficie e vedere i risultati. I numeri cambiano di nuovo e sembra dover accettare sempre di più il fatto che, per sapere come comportarsi nella prima superficie, i fotoni debbano sapere come si comportano gli “altri” nel passaggio di tutte le superfici. Un caos terribile, degno di un pazzo. E invece, tutto ciò è esprimibile e spiegabile matematicamente. Questa è la QED e questo vuol dire che è assolutamente incomprensibile anche per un genio come Feynman!

Fatemi ancora ripetere il concetto di base: “la scelta di un fotone quando incontra la prima superficie dipende da quali saranno le decisioni degli altri fotoni di fronte alle altre superfici”. Una decisione corale che sembra non tener conto del tempo e del suo scorrere.

Attenzione. Uno potrebbe facilmente rispondere a queste assurdità, considerando la luce come onda e scartando l’ipotesi delle particelle. Purtroppo le prove giocano a sfavore di questa scappatoia: se diminuiamo progressivamente l’intensità della luce, ci rendiamo conto che i rivelatori continuano a ricevere segnali della stessa intensità (ossia con lo stesso codice di frequenza se il colore è uno soltanto). Ciò che cambia è il numero di segnali ricevuti nell’unità di tempo. Ciò dimostra, al di fuori di ogni dubbio, che si stanno misurando particelle che o esistono o non esistono. Possono diminuire di numero ma non cambiare la loro caratteristica.

Non pensiate che tra poco capiremo perché capita tutto ciò. Nessuno è in grado di farlo. Tutto ciò che si riesce a fare è calcolare esattamente, attraverso una teoria perfetta, la probabilità che la luce sia più o meno riflessa da una superficie. Nessuno è ancora riuscito a spiegare perché e come un fotone decide di comportarsi. La QED ci permette, però, di calcolare esattamente la probabilità di ottenere un certo risultato a seconda delle condizioni in cui siamo.

Feynman dà particolare risalto all’esempio della riflessione parziale (un perfetto esempio per spiegare come agisce la teoria), ma lo stesso tipo di trattazione e di spiegazione si applica a TUTTI i fenomeni in cui vi è interazione tra luce e materia. Questo fa della QED un gioiello fisico assoluto, assurdo -se volete- ma preziosissimo!

Per potere effettuare il calcolo dell’esatta probabilità (l’unica cosa possibile) è necessario introdurre una semplice freccia, di direzione e lunghezza variabili, e munirsi di un foglio di carta. Se poi riuscissimo a scovare anche un cronometro, non sarebbe male, ma può anche bastare un semplice orologio calibrato adeguatamente. La semplicità delle scoperte eccezionali!

La prossima puntata passeremo anche noi all’azione, proprio con questi mezzi a disposizione di tutti. Non vi è bisogno di supercomputer, di formule complicatissime (si possono evitare tranquillamente), di costruzioni geometriche da far girare la testa. No, solo tanta umiltà, attenzione e voglia di sapere.

Il giallo continua… e sarà sempre più avvincente. Credetemi!