Ricapitoliamo

Cosa abbiamo imparato fino ad adesso? Riassumiamo brevemente i concetti fondamentali. Innanzitutto abbiamo stabilito che la luce viene trasportata da particelle. La prova? Decisiva! Quando la luce di un solo colore (monocromatica) colpisce un rivelatore, si “sentono” nettamente i fotoni che la colpiscono. Inoltre, diminuendo la luminosità, ciò che si ottiene è la riduzione dei segnali che arrivano, ma la loro singola “intensità” non cambia.

Abbiamo poi stabilito, con non poco imbarazzo, che se la luce colpisce una superficie di vetro, alcuni fotoni vengono rimandati indietro, mentre altri (la maggioranza) proseguono all’interno del vetro. Comunque si cerchi di spiegare questo fatto non si riesce a capire perché qualche fotone scelga di rimbalzare e altri no. Soprattutto, non si riesce a stabilire chi di loro prenda una o l’altra decisione.

Se si aggiunge una seconda superficie riflettente, a breve distanza dalla prima, le cose diventano ancora più misteriose. Il numero totale di fotoni che subiscono una riflessione, o sulla prima o sulla seconda, invece di essere il doppio di quelli osservati con una sola superficie possono variare da zero fino a un valore massimo, superiore a ciò che ci si poteva aspettare. Sembra proprio che i fotoni che rimbalzano sulla prima superficie debbano attendere cosa facciano quelli sulla seconda per prendere una decisione. Assurdo, veramente assurdo. Malgrado una situazione di totale incomprensione, siamo riusciti ad affrontare e a descrivere il fenomeno considerando solo la probabilità di rimbalzare dei fotoni e, addirittura, di calcolare il risultato finale con due o più superfici. Ci si è riusciti attraverso delle semplici frecce e un ottimo cronometro ultra rapido. Ovviamente, si sono dovute seguire alcune regole molto precise:

1) La probabilità che accada un evento è data dal quadrato della lunghezza di una freccia che abbiamo chiamato ampiezza di probabilità.

2) Per calcolare la probabilità finale di un evento che ammette più vie alternative, basta disegnare un’ampiezza di probabilità per ogni alternativa (ogni “scelta” ?) e combinarle insieme secondo lo stesso metodo che ci permette di sommare dei vettori.

Non dimentichiamo, però, che è necessario anche usare un cronometro che sappia scandire il movimento dei fotoni per determinare la direzione delle frecce. Un cronometro che gira in modo diverso a seconda del codice-colore del fotone. Più lentamente per il rosso e più velocemente per il blu.

Applicheremo, adesso, queste semplici regole ai principali fenomeni naturali che vedono la luce come protagonista. Lo faremo per i più comuni e conosciuti, ma Feynman ci assicura (e non possiamo fare altro che crederci) che il successo è garantito anche per fenomeni molto più complicati, come la diffrazione e anche “peggio”.

Uno specchio tuttofare

Iniziamo proprio con il fenomeno che ci è servito per introdurre le regole enunciate precedentemente, ossia la riflessione della luce. In poche parole, vogliamo descrivere come la luce si riflette su una superficie e perché  l’angolo di incidenza è uguale all’angolo di riflessione.

Ricordiamo brevemente cosa ci dice l’ottica geometrica “normale” e come si rappresenta la riflessione. Si considera una sorgente di luce S, uno specchio e un rivelatore R. Si traccia un bel raggio di luce che arriva sullo specchio in un certo punto M (non è un punto qualsiasi!), si calcola l’angolo tra la superficie e il raggio (o il suo complementare) e lo si riporta tale e quale dall’altra parte del punto. Il nuovo raggio finisce, ovviamente, sul rivelatore R. Lo vediamo nella Fig.14. Quante volte abbiamo disegnato questo semplice e logicissimo schema?

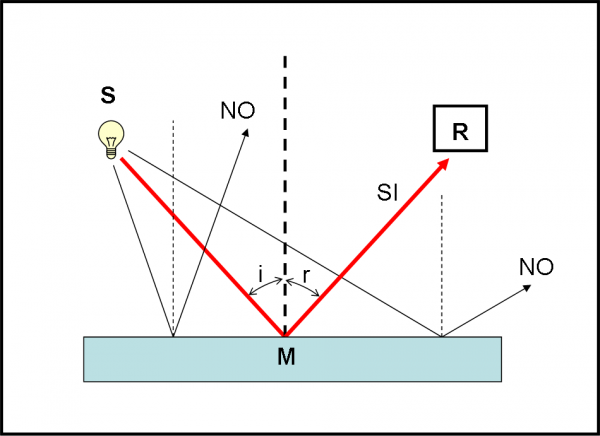
Ebbene, cerchiamo di cambiare un po’ il nostro modo di pensare, come potrebbe fare Alice. Per quale motivo abbiamo disegnato un solo raggio che lascia la sorgente S? In fondo, sappiamo benissimo che i fotoni possono andare in qualsiasi direzione. Perché scegliere solo la direzione che ci fa comodo? Perché trascurare tutte le altre? Un po’ alla volta questo modo di ragionare così “normale” comincia ad apparirci illogico. E’ come se avessimo fatto una scelta arbitraria che favorisce certi fotoni solo perché sappiamo il risultato finale, senza curarci della realtà dei fatti.

D’altra parte i rivelatori ci hanno dimostrato senza ombra di dubbio che i fotoni sono corpuscoli che sembrano viaggiare in linea retta e che quando arrivano sul rivelatore ci informano attraverso il loro “tac”. Dobbiamo trattarli così e analogamente dobbiamo accettare che essi vadano in ogni direzione. Ciò vuole anche dire che i fotoni che partono da una sorgente possono toccare qualsiasi punto dello specchio e non solo il punto M che ci mostra la riflessione di un SOLO raggio e che si trova per ovvi motivi geometrici proprio alla stessa distanza da S e da R.

Potremmo concludere che sì, è vero che vi sono molti altri raggi, ma nessuno di essi, riflettendosi, può raggiungere il rivelatore R e, di conseguenza, li possiamo tranquillamente trascurare e concludere che vale la pena disegnare solo quello che serve. In altre parole, potremmo concludere che i fotoni che colpiscono lo specchio vicino ai suoi estremi (più vicini a S e a R) non abbiano niente a che fare con quelli che hanno la possibilità di raggiungere R, come sembra indicare perfettamente la Fig. 14.

Se, però, questo ragionamento comincia a sembrarci troppo semplicistico, come se cercasse di mettere la polvere sotto al tappeto, vuol dire che abbiamo buone possibilità di seguire Alice nel suo mondo assurdo. La MQ ci ha ormai segnato e il dubbio che si stia sbagliando a vedere le cose in modo troppo “normale” diventa sempre più forte.

Serviamoci ancora della stessa Fig. 14, ma la ridisegniamo come Fig. 15. Non cambia la situazione, ma cambia il modo di affrontare il problema. La sorgente S “spara” un fotone alla volta, dello stesso codice, per esempio il codice “rosso”. Qualsiasi traiettoria dei fotoni che partono da S è possibile e nessuna va trascurata. In R mettiamo il solito rivelatore di fotoni.  Cosa dobbiamo fare per seguire gli insegnamenti della QED? Dobbiamo calcolare la probabilità di arrivare su R di qualsiasi fotone, dopo che ha toccato lo specchio. Nessuno è favorito a priori e lavoriamo in modo del tutto imparziale, come dovrebbe fare qualsiasi VERO arbitro di una partita di calcio.

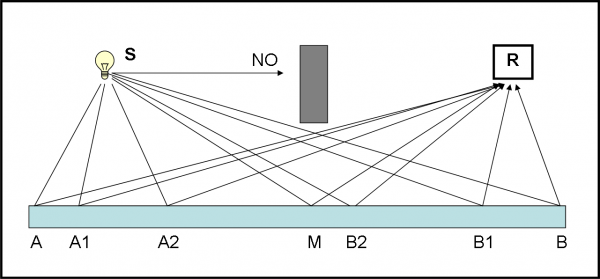
Per evitare che qualche fotone prenda una scorciatoia (i fotoni ne sanno una più del diavolo), mettiamo uno schermo tra sorgente e rivelatore, in modo che i “furbi” che volessero prendere la direzione diretta da S a R vengano bloccati. Liberata la mente da riflessioni troppo comuni e razionali, immergiamoci completamente in quello che ci ha insegnato, finora, la QED. Applichiamo, quindi, le regole che conosciamo.

La probabilità che un certo evento si verifichi è il quadrato della freccia finale che si ottiene combinando assieme tutte le frecce delle varie possibilità che possono portare all’evento finale. Non spaventatevi… è proprio quello che abbiamo fatto usando la lamina di vetro. In quel caso vi erano solo due possibilità per raggiungere R1: o attraverso la riflessione sulla prima superficie o sulla seconda. Ricordatevi che per calcolare la probabilità finale abbiamo proprio combinato due frecce relative a queste due possibilità di azione.

Nel “nuovo” esperimento le cose si complicano non poco (apparentemente), dato che vi sono milioni o miliardi, o il numero che volete, di possibilità per far giungere la luce di S in R. Il tragitto del fotone, infatti, non è assolutamente legato a ciò che noi vogliamo dimostrare (angolo di incidenza uguale all’angolo di riflessione), ma segue tutte le possibili vie che ha a disposizione. Non possiamo certo limitarne le possibilità sapendo qual è il risultato. Vale proprio il contrario: considerando tutte le vie di manovra dobbiamo dimostrare che l’angolo di incidenza è uguale a quello di riflessione. Il discorso è completamente diverso!

Accettiamo, quindi, stringendo i denti e annullando tanti concetti imparati a scuola, che i fotoni possano fare tutti i percorsi possibili, colpendo lo specchio in qualsiasi suo punto e poi giungere, comunque, in R, “fregandosene” bellamente delle regole dettate dal buon senso. Quanto detto è rappresentato nella Fig. 15, dove abbiamo disegnato solo qualche percorso possibile. Non sentiamoci “pazzi” perché stiamo accettando un qualcosa che sappiamo che non “dovrebbe” essere logico. Affidiamoci solo e soltanto alle probabilità.

Per essere ancora più chiari, eseguiamo una semplificazione che non cambia certamente il risultato (lo abbiamo imparato studiando la definizione di limite e cose del genere).  Consideriamo il nostro specchio sotto forma di striscia e dividiamolo in tanti tasselli quadrati tutti uguali tra loro. Accettiamo, inoltre, che per tutti i punti del tassello la luce si comporti in un solo modo, come descritto in Fig. 16. Spieghiamoci meglio. Sappiamo benissimo che ogni punto dello specchio colpito dalla luce dà luogo a una certa freccia probabilistica, ossia dà luogo a un comportamento diverso dai punti adiacenti. Per trattare, però, milioni e milioni di punti, con comportamenti diversi,   dovremmo fare uso, quantomeno, degli integrali. Molto meglio, dividere lo specchio in piccoli tasselli di dimensioni “finite” e assumere che ognuno di essi dia luogo a un certo comportamento.

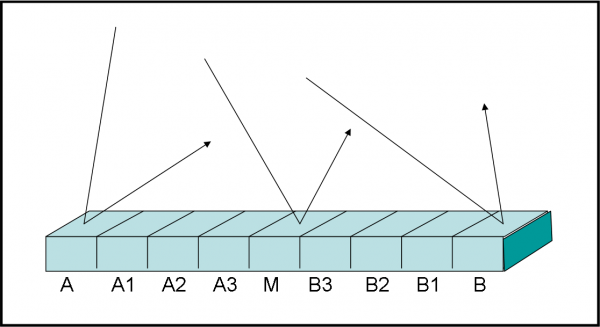
Il risultato che otteniamo è soltanto più approssimato, ma non cambia più di tanto. Sicuramente è più che sufficiente per i nostri scopi. Niente ci vieta, inoltre, di migliorare la rappresentazione riducendo sempre più le dimensioni dei singoli tasselli, facendoli un po’ alla volta tendere verso dimensioni nulle (e qui saltano fuori i concetti di limite e via dicendo…). Non lo faremo, proprio perché non vogliamo introdurre le formule molto “cattive”, ma perfette, che sono il punto di forza della QED. Accontentiamoci e non ce ne pentiremo!

Fatte queste premesse, possiamo concludere che ogni tassello è caratterizzato da un’unica freccia che ha una certa lunghezza e una certa direzione. Cominciamo con la lunghezza. Nuovamente non facciamo il solito errore a cui ci porta la logica comune. La lunghezza di una freccia indica, in pratica, la probabilità che ha un fotone che arriva su di esso di rimbalzare esattamente sul rivelatore R. Verrebbe da dire che la probabilità è sicuramente massima per il tassello (chiamiamolo pure punto) che sta a metà dello specchio, ossia in M. Ne dovrebbe seguire che la lunghezza di questa freccia debba essere la massima. Ovviamente, commetteremmo un errore, dato che partiremmo condizionati dal risultato che tutti conoscono nell’esperienza comune. Analogamente, saremmo portati a disegnare una lunghezza piccolissima per le frecce di A e B. No, no… dobbiamo seguire le regole imparate nell’articolo precedente. Un fotone che arriva in un qualsiasi punto ha “praticamente” sempre la stessa probabilità di dirigersi da qualsiasi parte esso voglia. Attenzione: in realtà una leggerissima differenza esiste, ma è talmente insignificante che possiamo trascurarla (parola di Feynman e delle sue formule). Possiamo perciò considerare costante la lunghezza della freccia relativa a ogni punto (o -meglio- tassello). Il che vuol dire che anche il suo quadrato rimane costante e quindi anche la probabilità del singolo evento. Questo concetto è veramente fondamentale per tutta la MQ: la probabilità relativa a una qualsiasi "scelta" fatta dal fotone è sempre la stessa. Il fotone ha  la stessa probabilità di raggiungere qualsiasi punto ( e anche -come vedremo- di seguire  qualsiasi traiettoria). Tutta la MQ si fonda su questo semplicissimo principio: la realtà si descrive così. Punto e a capo!

La stessa cosa, però, non succede certo per la direzione della freccia. La direzione dipende da quanti giri ha fatto la lancetta del cronometro tra la partenza del fotone da S e il suo arrivo in R. Tuttavia, i percorsi SR sono ben diversi a seconda del punto in cui il fotone tocca lo specchio. Maggiore o minore è il percorso e maggiore o minore è l’angolo della direzione finale della lancetta rispetto a una certa direzione di riferimento. Ricordiamoci che tutti i fotoni hanno lo stesso codice e quindi il cronometro gira alla stessa velocità per tutti.

Consideriamo la Fig. 17. Due fotoni seguono due percorsi differenti. Il primo tocca lo specchio in A e il secondo in M.  Entrambi devono poi arrivare fino a R. Beh, non c’è QED che tenga: il percorso SAR è sicuramente più lungo di SMR. Percorso più lungo vuole dire posizione diversa della lancetta del cronometro che ha dovuto compiere una frazione di giro in più (o magari anche molti giri completi più una frazione di giro). In altre parole, c'è voluto  più tempo per descrivere il percorso SAR che non quello SMR. La velocità del cronometro è sempre la stessa, ma il percorso ha lunghezza differente.

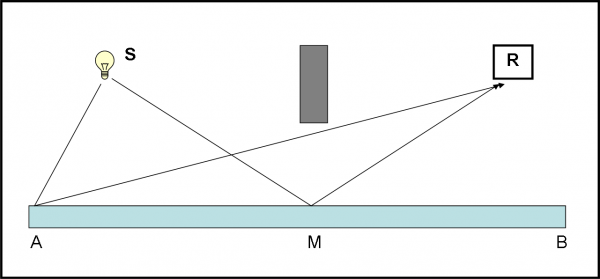
Introduciamo un nuovo tipo di figura decisamente comoda e comprensibile. Per ogni punto dello specchio colpito, il percorso SR ha lunghezza diversa e di conseguenza varia il “tempo” (giri e frazioni di giro) misurato dal cronometro dalla partenza all’arrivo del fotone corrispondente (la velocità è la stessa) . La Fig. 18a rappresenta schematicamente i percorsi eseguiti dai vari fotoni che abbiamo considerato (forse sarebbe meglio dire il percorso scelto da ogni fotone per arrivare in R), mentre la Fig. 18b descrive proprio la relazione tra posizione del punto colpito e tempo di percorrenza del tragitto relativo. In poche parole, inseriamo come ascissa la distanza di ogni punto dello specchio rispetto ad A (per esempio) e in ordinata il “tempo” impiegato dal fotone che ha colpito lo specchio in quel punto, per andare da S a R.

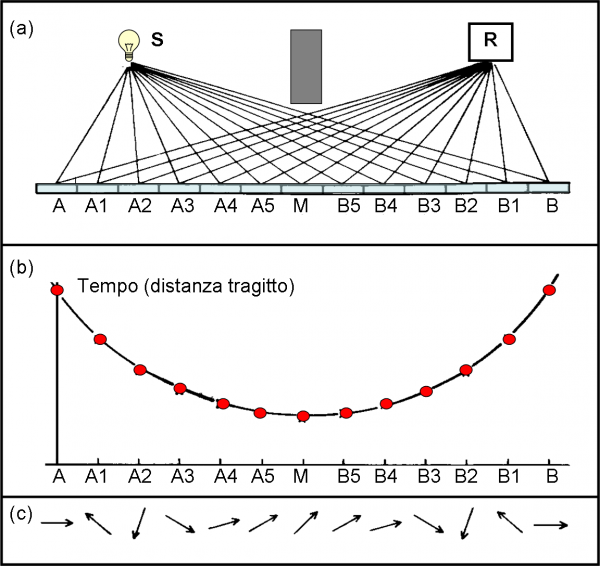
Otteniamo una specie di parabola (unendo i punti vediamo proprio una parabola disegnata a “scatti”, che sarebbe sempre più raffinata aumentando i punti). All’inizio (in A) il tempo è molto lungo. A mano a mano che il punto si avvicina a M il tempo diminuisce. Superato M il tempo ricomincia ad aumentare fino ad arrivare in B, dove è ovviamente uguale a quello di A per come è stato rappresentato lo specchio, la sorgente e il rivelatore.

Possiamo anche vedere (e questo fatto è veramente importante!) che spostandoci anche di poco rispetto ad A il tempo cambia sensibilmente, mentre avvicinandosi a M la variazione decresce sempre di più. L’andamento si ripete andando da M verso B. Conoscere bene le caratteristiche della funzione “parabola”, o quello che è, può servire moltissimo se volessimo scrivere le formule relative (ecco perché è importante lo studio delle funzioni…).

Quanto detto per i tempi si trasferisce immediatamente alla direzione della lancetta del cronometro. Vicini ad A la differenza di direzione della  freccia varia notevolmente da punto a punto, mentre vicini a M la lancetta cambia di poco la direzione, che si mantiene pressoché costante. Poi, ricomincia a variare sempre di più, giungendo in B con la stessa direzione di A, dato che il percorso SAR è uguale, per costruzione, a SBR. Possiamo, perciò disegnare al fondo della Fig. 18 (Fig. 18c) le frecce calcolate punto per punto, con lunghezza costante e direzione più o meno variabile a seconda del tempo impiegato o –meglio ancora- dello spostamento della lancetta.

Ovviamente, abbiamo scelto la direzione della freccia di A qualsiasi (poco importa). Quelle successive hanno però una stretta correlazione con la prima, seguendo quanto detto precedentemente.

Non ci rimane, adesso, che “sommare” tutte le frecce, ossia combinarle con le regole imparate la volta scorsa. Prima di farlo, devo fare un'importante precisazione. Nell’esperimento della lastra di vetro dell’articolo precedente, avevamo invertito il verso della prima freccia e non quello della successiva. La regola non vale più in questo caso, dato che la riflessione avviene nello stesso modo per tutti i percorsi. In altre parole, la freccia gira di 180° o non gira affatto, a seconda del materiale in cui avviene la riflessione. Ricordiamoci, infatti, che stiamo sempre usando la semplificazione che dice di considerare una riflessione come fenomeno che coinvolge solo la superficie. In realtà non è così, ma per essere più esatti dovremmo sapere fare interagire fotoni con materia. E questo lo faremo solo più in là. Accettiamo, quindi, queste rotazioni di mezzo giro che a volte si compiono e a volte no, come un piccolo atto di fede che risolveremo in seguito. Nel caso in esame, abbiamo la riflessione su vetro, provenendo da aria, per tutti percorsi effettuati dalla luce. Non vi è quindi bisogno di introdurre capovolgimenti di verso della freccia.

Un bel "lento" o un bel "tango"?

Torniamo al caso in oggetto e combiniamo le frecce mantenendo per tutte il verso della lancetta. Il risultato è oltremodo simpatico e intrigante, come mostrato in Fig. 19.

Non solo è simpatico, ma anche descrivibile molto bene. Le prime frecce, vicine ad A, cambiano drasticamente direzione e ciò vuol dire che in pratica la loro combinazione fa tanto fumo e poco arrosto: la freccia finale, relativa a loro, rimane piccola. Ricordate l’analogia con la “danza”? Ebbene, vicini ad A è come se ballassimo un lento. Ogni passo avviene in una direzione completamente diversa da quella precedente, ma alla fine si rimane sempre sulla stessa “mattonella”. Le cose invece cambiano drasticamente avvicinandosi a M. I vari passi sono, adesso, tutti diretti verso una direzione quasi costante. La combinazione di queste frecce così simili porta a uno spostamento non certo trascurabile. Poi, andando verso B le frecce tornano ad essere caotiche e “inconcludenti”. Ne segue che la freccia finale, dipende essenzialmente dalla direzione, quasi costante, delle frecce vicine al punto medio M. Vi prego di non prendere la figura come una disegno precisissimo: l’ho tracciata un po’ a occhio e con ovvie approssimazioni. Ricordiamoci, comunque, che la lunghezza delle singole frecce deve essere sempre uguale.

Non perdiamo di vista lo scopo di questo bel gioco di frecce e lancette. Ciò che volevamo trovare era proprio la direzione e la lunghezza della freccia finale, il cui quadrato indica proprio la probabilità di avere una riflessione sullo specchio e raggiungere R. Ci siamo riusciti e abbiamo visto che questa probabilità è alta (dipende dalla lunghezza della freccia finale) ed è essenzialmente legata alla somiglianza della direzione delle frecce vicine al punto di mezzo dello specchio. Attenzione: la direzione della freccia finale, in sé, conta poco; quello che conta è la lunghezza della freccia finale o, se preferite, dalla costanza della direzione delle frecce che permette di sommare veramente la loro lunghezza. In altre parole, ciò dimostra che per raggiungere il rivelatore M è molto meglio che il fotoni tocchino lo specchio vicino al punto di mezzo, dove l’angolo di incidenza è quasi uguale all’angolo di riflessione e il “tempo” impiegato è  quello minimo. Questa è la zona dello specchio che dà il massimo contributo alla probabilità totale  che l'evento (riflessione) avvenga.

Se guardiamo bene la Fig. 19, notiamo che il risultato finale non sarebbe cambiato di molto se avessimo eliminato il contributo delle prime frecce a sinistra e delle ultime a destra. In parole povere, chi comanda sono le frecce vicine a M. Questa conclusione può approssimarsi nella visione del mondo normale, che dice che i fotoni che partono da S, e si riflettono sullo specchio raggiungendo R, lo fanno colpendo lo specchio nella parte mediana, ossia con un angolo di incidenza uguale all’angolo di riflessione, impiegando il minor tempo possibile per andare da S a R.

Possiamo anche fare un’ulteriore considerazione: le probabilità che i fotoni che colpiscono lo specchio vicini ad A e a B, e poi raggiungono R, sono del tutto simili a quelle della parte mediana dello specchio, ma esse sono talmente “variabili” che le loro probabilità praticamente si annullano a vicenda , quando vengono combinate. Troppa agitazione porta, veramente, a poco o niente. La calma e la costanza delle frecce mediane, invece, premia, dato che le frecce si sommano dando luogo a una probabilità finale decisamente grande.

Solo dopo aver fatto questa riflessione possiamo dire di  escludere tranquillamente le parti laterali dello specchio e ottenere lo stesso risultato! Inoltre, ragionando in termini di probabilità, il fatto che la probabilità che capiti un evento composto da due eventi, possa essere minore o maggiore della probabilità di un singolo evento, diventa un risultato del tutto “normale”. L’esperimento della lastra di vetro della volta scorsa perde molto della sua assurdità, che sembrava mostrare che i primi fotoni decidessero qualcosa solo dopo che i secondi avevano fatto la loro scelta? Sembrerebbe di sì, dato che l’annullamento o la somma delle probabilità dipende solo dalla direzione delle frecce.

No, no, non cerchiamo di riportare Alice nel nostro mondo. Resta sempre il problema di partenza. Perché un fotone decide di andare in una direzione e non in un’altra, di attraversare o non attraversare il vetro? La QED ci permette di ottenere il risultato finale con estrema esattezza, ma non riesce assolutamente a spiegare il perché! Un po’ alla volta, iniziamo a capire che le particelle non possono sempre essere trattate come tali e che a ognuna di esse bisogna collegare o sostituire (o quello che volete) la probabilità e non la certezza di un fenomeno di fisica classica.

Insomma, abbiamo capito benissimo che tracciare la solita retta che parte da S, arriva in M e giunge, infine, in R è solo e soltanto un’approssimazione di un comportamento più complesso descritto dalla QED! Sembrerebbe un’inutile perdita di tempo, dato che si ottiene lo stesso risultato della fisica classica, ma studiando meglio la situazione, vedremo che è in realtà molto più corretto (e utile) accettare che tutta la superficie dello specchio concorre al fenomeno della riflessione. Troppo semplice e parziale limitarci a una sola direzione privilegiata. Entrando nella logica illogica della MQ, cominciano veramente ad apparire troppo limitativi gli espedienti usati nella fisica classica per spiegare certi fenomeni all’apparenza molto, anzi troppo, ovvi.

La prossima volta studieremo meglio la situazione, divertendoci a sezionare lo specchio… e anche a fare degli strani giri di danza (valzer, tango, ecc…).

Fermiamoci a riflettere e non picchiatemi

Un consiglio… mentre andiamo avanti con questa descrizione essenzialmente grafica e un po’ empirica, cercate di confrontare certi concetti (espressi in modo diverso) con quelli che avevamo “toccato” spiegando l’esperimento della doppia fenditura. Vi renderete conto che stiamo dicendo le stesse identiche cose… Uno sforzo non trascurabile, senza far uso di formule esatte, ma molto stimolante e fondamentale per capire quanto sia incomprensibile la MQ e quanto sia corretta e precisa nel descrivere la Natura. Invece di sprecare tempo e capacità mentale a immaginarsi stringhe, universi paralleli, buchi neri e buchi bianchi che si accavallano, tempi che rallentano, accelerano e/o invertono la loro freccia, dedichiamoci PRIMA a capire le basi della MQ, ormai perfettamente descrivibili con esempi semplicissimi. Senza di esse qualsiasi sproloquio sulle ultime teorie dell’Universo diventa un falso Picasso…

Non odiatemi per la ripetizione di questo concetto che sembra negare la fantasia e l’immaginazione. Lo faccio sia per voi che per me stesso. La fantasia è meravigliosa solo se poggia su una conoscenza completa di ciò che vogliamo estrapolare e inventare. Altrimenti è solo e soltanto un gesto di arroganza e di superficialità…