Divertiamoci un po’ con il nostro specchio e le sue frecce vagabonde. Impareremo molte cose interessanti. Molte altre le intuiremo soltanto non potendo scendere troppo nei dettagli. Abbastanza, però, per far venire voglia a qualcuno di procedere da solo.

A che servono i bordi dello specchio?

Innanzitutto, vogliamo dimostrare, in modo assoluto, quanto abbiamo detto un po’ vagamente, ossia che le parti laterali dello specchio non danno praticamente contributo alla riflessione della luce, dato che le frecce si eliminano una con’altra. Non ce ne sarebbe bisogno, dato che è già abbastanza intuitivo, ma prendiamolo come un “gioco” distensivo in vista di qualcosa di un po’ più impegnativo.

Per giungere a una conclusione veramente efficace, eliminiamo letteralmente (coprendolo con un cartone) tutto lo specchio tranne una zona molto vicina ad A (Fig. 20).

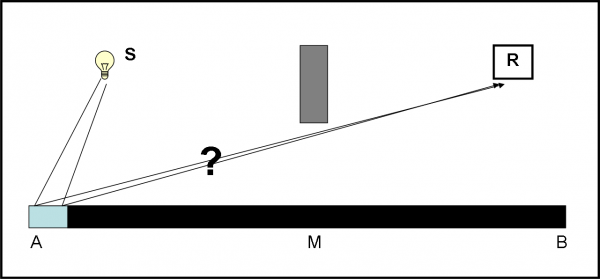
Per essere ancora più precisi diciamo che teniamo quella parte di specchio dove il tempo di arrivo su R varia di molto ma pressoché linearmente con la distanza da A (Fig. 18b). Non ci tragga in inganno la Fig. 18a. La freccia è indicata solo in alcuni punti. Tra uno e l’altro la direzione varia molto, quando si è vicini ad A. Tuttavia, non pensiamo che tra SAR e  SA1R, ad esempio, la freccia abbia solo fatto una frazione di giro. Il cronometro è talmente veloce che ha probabilmente fatto molti giri più una frazione… Basta un piccolo spazio in più da percorrere e la freccia gira molte volte. Vicini ad M, invece, la freccia non è riuscita proprio a girare, dato che i percorsi sono veramente simili tra loro.

Per vedere bene la reale situazione bisogna indicare molti più punti lungo lo specchio. Fatte queste dovute precisazioni, vediamo in dettaglio cosa capita se lasciamo scoperto solo un pezzetto di specchio vicino ad A. Questa volta, possiamo assumere che tra un punto e quello successivo la freccia abbia veramente girato di una frazione di giro in più. E lo ha anche fatto in modo abbastanza uniforme (ecco perché ho detto di rimanere nella zona in cui la parabola coincide praticamente con una retta).

Nella Fig. 21, i punti indicati stanno quindi in un intervallo molto piccolo di specchio, tutti compresi, per esempio, tra A e A1. Nella parte alta vediamo come variano le direzioni delle frecce. Come previsto, la differenza, da punto a punto, rimane, comunque, molto grande dato che il tempo tra partenza e arrivo cambia sempre abbastanza. Aumentando i punti e diminuendo la distanza fra loro è molto più facile, però, seguire come varia veramente la direzione della freccia. Sotto alla parte dello specchio usato, sono state disegnate le frecce relative.

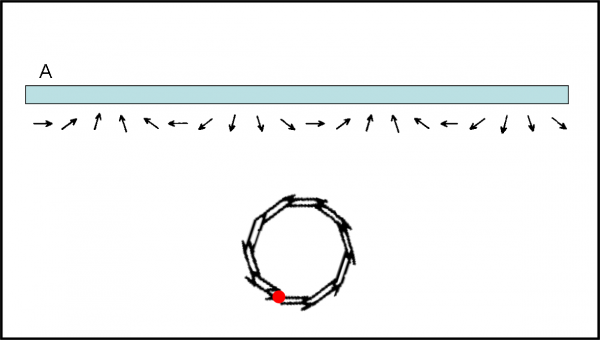
E’ immediato vedere che tra una e l’altra, lo spostamento angolare rimane quasi costante (il tempo -e, quindi, il percorso- varia linearmente). Diventa un gioco da bambini combinare le frecce tutte assieme secondo la ormai famosa regola, come fatto nella parte bassa della figura. Ci dobbiamo stupire se esse girano in tondo per due volte, tornando al punto di partenza? Direi proprio di no, c’era da aspettarselo! Questo simpatico girotondo di frecce cosa ci dice? Che la freccia finale, combinazione di tutte quelle del nostro pezzo di specchio, ha una lunghezza esattamente uguale a ZERO. In altre parole, la probabilità di avere una riflessione della luce in grado di raggiungere R è nulla. Potevamo eliminare questo pezzo di specchio e niente sarebbe cambiato.

Qualcuno mi dirà: “Che scoperta! Era veramente assurdo aspettarsi che la riflessione potesse arrivare in R attraverso uno specchietto posto sotto alla sorgente, con R molto più spostato verso destra. Bastava tracciare poche linee e l’ottica geometrica ce l’avrebbe detto subito”. In effetti, sembrerebbe proprio di aver perso un mucchio di tempo a far girare inutilmente una freccia la cui “somma” ha dato zero. Bastava limitarsi alla zona vicino a M e cercare la traiettoria di minore lunghezza  (quella che il fotone ha percorso in minor tempo) per dire che lì ci sarebbe stata la massima probabilità di riflessione.

Ecco che la logica “normale” cerca di riprendere il sopravvento e ci sta convincendo che non vi è nessun bisogno di parlare “solo” in termini di probabilità. E’ molto meglio tornare alla vecchia e sicura fisica classica e all’ottica geometrica.

Il gioco dei tre… cartoni

Datemi, però, un’altra possibilità, sempre con la parte di specchio che sembra del tutto inutile. Faccio una cosa abbastanza strana, ma molto, molto interessante. La “maschero” ancora di più, ma stando bene attento alle parti che copro con il cartone. La figura è sempre la Fig. 20, ma, questa volta, con alcune zone, del residuo di specchio, rese impossibilitate a riflettere. Vedo già il sorriso di qualcuno: “Povero illuso! Se tutto lo specchietto non era capace di riflettere la luce su R, come puoi pensare minimamente che riesca a farlo lo stesso specchietto mascherato in più parti. Se  tutto non ci riesce, non ci riesce, a maggior ragione, la sua metà o anche meno, anche se mascherata a strisce…”. Io rispondo soltanto: “Vogliamo provare?” e disegno la Fig. 22.

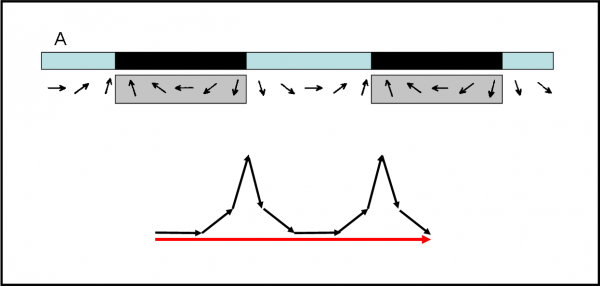
Sono stato, ovviamente, molto attento a quale parte nascondere e quale lasciare libera, ma alla fine ottengo la parte alta della Fig. 22. Coprendo alcune parti dello specchietto, sempre più piccolo, ho eliminato le frecce che corrispondono alle zone ora nascoste. Se queste sono coperte dal cartone, la probabilità di riflettere non può che essere zero: va bene dire assurdità, ma un pezzo di cartone non può riflettere nemmeno nella QED.

Non mi resta allora che prendere le frecce che mi rimangono e combinarle assieme, sempre secondo la celeberrima regola vettoriale. Il risultato è mostrato nella parte bassa della figura. Vi sembra una probabilità nulla? Assolutamente no, anzi è decisamente alta! Quello che non era riuscito a fare uno specchietto messo nella posizione sbagliata è riuscito a farlo coprendone ancora qualche parte. Se non è assurdo questo… Eppure, non ho fatto altro che descrivere il funzionamento (probabilistico) di un reticolo a diffrazione. E dico poco… Tutto ciò solo e soltanto con quelle piccole frecce che sembravano non servire a niente.

Facciamo subito una constatazione che ci serve a “spiegare” anche l’esperimento della doppia riflessione. Nello specchio mascherato di Fig. 22 abbiamo eliminato, in pratica, solo le frecce che puntano verso sinistra e abbiamo tenuto quelle che puntano verso destra. Potevamo fare il viceversa e avremmo ottenuto lo stesso identico risultato. Si può quindi facilmente concludere che lo specchio perde le sue capacità, dando probabilità finale nulla, quando si combinano assieme le frecce che puntano a sinistra e quelle che puntano a destra. L’analogia con la doppia riflessione è perfetta. Se le frecce delle due riflessioni vanno nello stesso verso la probabilità finale si amplifica, ma se vanno in verso opposto la probabilità si annulla del tutto.

Toniamo al nostro personale reticolo di diffrazione e vediamo quale altra cosa sa fare. Innanzitutto dobbiamo ammettere che quello che abbiamo appena descritto è stato costruito su misura per la luce rossa. Se usassimo la luce blu (per la quale il cronometro gira più velocemente) dovremmo modificare le zone di specchio libere di agire. In particolare, dovremmo diminuire la distanza tra le strisce riflettenti, dato che il ciclo probabilistico del blu è più rapido.

Tuttavia, potremmo anche usare il reticolo del rosso, spostando il rivelatore R. La geometria cambia e così pure i percorsi che deve fare la luce. Troveremmo che, per una certa posizione, il reticolo rosso funziona perfettamente anche per il blu, come mostra la Fig. 23.

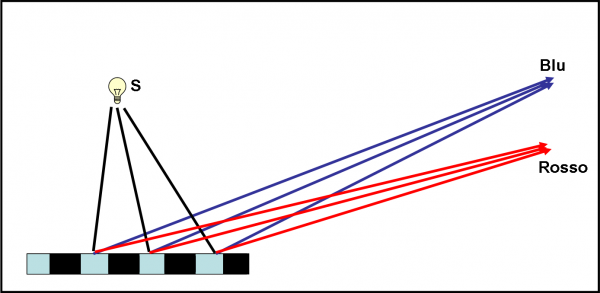
Analogamente, potremmo anche inviare luce bianca, quella solare, e vedremmo che spostando verso l’alto il rivelatore scorgeremmo prima la luce arancione, poi quella gialla per concludere con la verde e la blu. Insomma, proprio i colori dell’arcobaleno. Capite immediatamente che invece di spostare il rivelatore, potremmo benissimo costruire un rivelatore in grado di ricevere tutti i “codici” luminosi. La stessa cosa che fa un prisma a dispersione.

Ha senso, però, anche un’azione leggermente diversa: invece di spostare il rivelatore o allungarlo in qualche modo, possiamo lavorare sullo specchio, eseguendo moltissime scanalature vicinissime una alle altre. Capita che uno specchio del genere può dar luogo a riflessioni multicolori a seconda di dove viene colpito. E’ difficile da costruire? Nemmeno per sogno… pensate a un disco microsolco o a un “compact disc” come quello di Fig. 24.

Se vi dicessi che da questa semplice descrizione si arriva, con qualche difficoltà leggermente superiore, ai raggi laser e agli ologrammi e molto altro, vi stupireste ancora? No, penso proprio di no. Peccato non poter entrare nei dettagli, ma se analizzassimo tutti i fenomeni legati alla luce, non finiremmo mai. Resta il fatto, però, che la QED non ha alcun problema a descriverli tutti.

I reticoli naturali

Anche la Natura, però, ci sa fare e sfrutta lo stesso principio. Pur rischiando di andare un po’ oltre, vale la pena parlare del sale. Sì, proprio il sale da cucina. Sappiamo tutti benissimo che è composto da un mix di atomi di Sodio e di Cloro, legati saldamente tra loro secondo una struttura ben definita. Insomma, è uno dei tanti composti che hanno una struttura “cristallina”. Le distanze tra gli atomi sono quindi ben codificate.

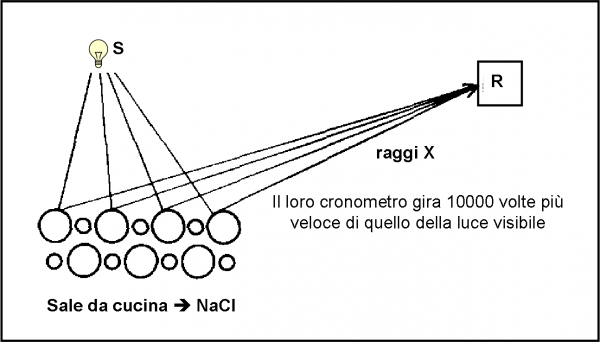
Capita così che gli atomi si comportino come zone riflettenti di uno specchio e formino un reticolo di diffrazione quasi perfetto. In particolare, esso è particolarmente utile per i raggi X, luce che normalmente non si vede e che ha un cronometro che viaggia ben 10 000 volte più velocemente di quelli della luce visibile. Possiamo, però, costruire un rivelatore per questi raggi e, attraverso la risposta che viene data spostandolo in posizioni diverse, stabilire la distanza tra gli atomi, ossia il “passo” del reticolo.

Ciò è già stato possibile nel lontano 1914, quando si è studiata per la prima volta la struttura dei cristalli, senza dimenticare che è stata una prova fondamentale per dimostrare che i raggi X fanno parte della radiazione elettromagnetica, ossia della luce. Ciò che avviene è descritto sommariamente in Fig. 25. Dobbiamo ammettere che alla natura piace proprio la QED, anche se la rende un po' più pazza e un po' meno comprensibile.

L’unione fa la forza… ma anche la debolezza

Concludiamo questa quarta parte con una constatazione di grande importanza per tutta la QED e la MQ. Avere dimostrato che qualsiasi parte di uno specchio contribuisce al fenomeno della riflessione ci dice che ogni parte dello specchio ha una sua freccia per qualsiasi evento possa avvenire, ossia qualsiasi possibilità ha una sua (ampiezza di) probabilità di verificarsi. In breve: tutto ciò che può capitare, prima o poi capita…

In altre parole, ancora, la singola freccia di ogni parte dello specchio ha una sua ampiezza di probabilità e quindi una probabilità di avvenire. Queste probabilità sono tutte uguali, perfettamente uguali. Non è quindi la probabilità di un singolo elemento a condizionare il risultato finale, ma la loro combinazione.

Abbandoniamo gli specchi e immergiamoci nella rifrazione. “Immergersi” è proprio il verbo adatto, in quanto studieremo come la luce passa dall’aria all’acqua. Il “giallo” continua, con buona pace del nostro amico pescatore (ricordate?).