Categorie: Meccanica Celeste
Tags: andamento rettilineo luce elettrodinamica quantistica La QED di Feynman percorso di minima distanza percorso di tempo minore probabilità QED rifrazione
Scritto da: Vincenzo Zappalà
Commenti:19
Feynman e la QED. 5: un bagnino esperto e degli ottimi vicini di casa **
Smettiamo di … “riflettere” e affrontiamo quel fenomeno che solitamente chiamiamo rifrazione. Lo spieghiamo o -meglio- lo descriviamo solo attraverso la QED e le sue regole. Ci aiuta in questa operazione un bagnino non solo impavido, ma anche calcolatore. Vi è, inoltre, un piccolo esercizio per tutti…e la spiegazione semplicissima del perché la luce SEMBRA andare in linea retta: basta scegliersi dei vicini di casa che collaborano volentieri. Forse l’uomo dovrebbe imparare a convivere con il suo prossimo, proprio come insegna la MQ. Mamma mia, quanta carne al fuoco!
Non aspettatevi niente di straordinario. Ormai la cosa veramente straordinaria l’abbiamo fatta nostra, utilizzando le frecce di probabilità -e la loro combinazione- per calcolare come e dove si ha la massima probabilità di ottenere un certo risultato. Passare dalla riflessione alla rifrazione non ha, quindi, bisogno di leggi diverse e di parametri particolari (come invece avremmo bisogno con l’ottica geometrica). Il succo di tutto è disegnare la direzione della freccia di ogni tragitto del fotone. Ma questo dipende solo e soltanto dalla lunghezza del percorso (o dal tempo impiegato a percorrerlo, misurato con il cronometro).
L’ampiezza di probabilità (freccia) relativa a ogni tragitto è, infatti, sempre la stessa, ma cambia di più o di meno la direzione della lancetta del cronometro, ossia la direzione delle singole frecce. Il tragitto che viene scelto (ossia che ha maggiore probabilità di verificarsi) è quello intorno al quale la lancetta resta praticamente nella stessa direzione, ossia quello di minima distanza tra sorgente e rilevatore e, ovviamente, anche di minimo tempo di percorrenza. Ma non sempre minimo tempo e minima distanza coincidono.
Queste frasi, ormai banali, ci dicono qualcosa di veramente importante che non deve scapparci e che è l’essenza stessa della MQ. Qualsiasi direzione prenda un fotone uscendo da una sorgente, la “particella”(continuiamo a chiamarla così) ha la stessa probabilità intrinseca di colpire un bersaglio. Insomma, può andare dove vuole e può arrivare comunque a segno. Tuttavia, la direzione dell’ampiezza di probabilità (freccia) varia in funzione del tempo che il fotone impiega per raggiungere la meta. Solo la combinazione delle frecce decide qual è la direzione favorita. In alcuni casi le frecce si arrotolano tra di loro e annullano la loro intrinseca probabilità o, al limite, la diminuiscono. In altri casi le frecce si distendono lungo una direzione quasi costante e la probabilità finale cresce decisamente. Solo studiando questo comportamento si può calcolare quale sia il tragitto più probabile, senza aver bisogno di sapere niente a priori. Nel caso della riflessione è anche il tragitto di minima distanza.
E’ o non è una conquista fantastica? Tutti i fenomeni luminosi vengono trattati con lo stessa identica e banale regola. Basta solo fare attenzione e applicarla correttamente. Ne consegue che dobbiamo continuare a usare sempre e comunque lo stesso tipo di procedimento utilizzato finora: niente di meno e niente di più.
Fatemi fare un esempio di tipo “politico”: due gruppi di persone vogliono unirsi per cercare di governare saggiamente la loro Nazione.
Il primo gruppo ha molta passione e volontà, ma ciascun individuo ha le proprie idee su come ottenere un certo risultato. Possiamo anche dire che ognuna ha una sua validità, ma troppo particolare. Bisognerebbe formulare una linea di condotta unitaria, fatta di piccoli compromessi, ma con una direzione ben precisa nella mente di tutti. Niente da fare. Il loro tempo viene sprecato a discutere e a cercare di distruggere le idee dei compagni piuttosto che unire gli sforzi. Il gruppo lavora moltissimo ma, alla fine, non ottiene niente e si sfalda: il loro partito non nascerà mai.
Il secondo gruppo ha idee altrettanto valide e anche personali, ma mette la singola convinzione in libero confronto con quelle degli altri. Cerca di estrarre le linee guida più unitarie possibili. Si accettano dei piccoli compromessi, non vince una sola idea, ma una combinazione di molte idee, abbastanza vicine tra loro. Dopo un tempo relativamente breve si forma il partito che riesce facilmente a convincere la popolazione a votarlo.
Fermi tutti! Non ridete… non è certo un esempio che calza con la politica odierna… è solo un sogno di fantapolitica al servizio di una Nazione, ma penso renda bene l’idea di base. In fondo, in fondo, per avere risultati corretti e condivisibili da tutti, basterebbe che anche le menti e i desideri dell’uomo seguissero le leggi della MQ . Le leggi della MQ sono improntate alla più larga libertà di azione, sapendo, però, che solo l’unità di intenti porta alla soddisfazione vera e completa. Se ogni mente umana seguisse le regole della QED (del buon senso e della ragione?), come fa un cristallo di sale, vivremmo in un mondo libero, felice, aperto e democratico!
Un uomo in mare!
Torniamo alla QED e dimostriamo subito come lo stesso procedimento usato per la riflessione funzioni perfettamente anche per la rifrazione della luce. L’esperimento consiste in un fotone che parte da una sorgente situata nell’aria e deve arrivare a un rivelatore posto in fondo a un lago, a un fiume o a un mare. In parole povere, la luce passa dall’aria all’acqua. Vi prego di non dirmi: “il rivelatore smetterebbe subito di funzionare!” Lasciatemi costruire un rivelatore indistruttibile!
Disegniamo velocemente la Fig. 26. In alto vi è il nostro “lago” o “mare”, con la sorgente S e il rivelatore “subacqueo” R. Come al solito, i tragitti che prende il fotone possono essere qualsiasi. Poi, arrivati sulla superficie dell’acqua, si dirigono tutti verso R. L'evento da studiare è : raggiungere R partendo da S. Bisogna calcolare dove si ha la massima probabilità di riuscita.
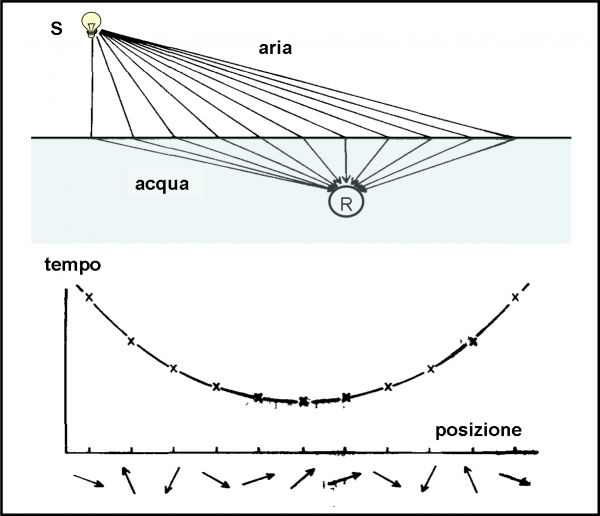
Attenzione, qualcuno potrebbe dirmi: “Perché dobbiamo considerare il cammino del fotone sempre rettilineo? E’ vero che sta andando dove vuole, ma potrebbe anche andarci seguendo linee curve…”. Avrebbe completamente ragione. E non potremmo nemmeno dire che il raggio è perpendicolare a un’onda circolare (è severamente vietato!). Tuttavia, nessuna paura: la QED ci mostrerà tra non molto che è proprio lei che descrive il moto rettilineo. Ne sa veramente una più del diavolo…
Torniamo alla Fig. 26. Sotto alla nuova configurazione, utilizzando sempre solo la luce rossa e il prezioso cronometro, riusciamo facilmente a tracciare la ben nota curva posizione del punto d’incontro con l’acqua-tempo di percorrenza e, conseguentemente, le ampiezze di probabilità (le frecce) per ogni punto considerato, con la loro direzione. Sembra di ripetere pari pari quanto fatto per la riflessione. Il risultato sembra anche lo stesso. Basta infatti combinare le frecce e otteniamo, in Fig. 27, la freccia finale che indica la probabilità di raggiungere il ricevitore. Ancora una volta, questa è piuttosto alta e il suo massimo contributo l’ottiene dalle frecce vicino al minimo della curva posizione-tempo, dove tra un punto e l’altro la lancetta del cronometro cambia di poco.
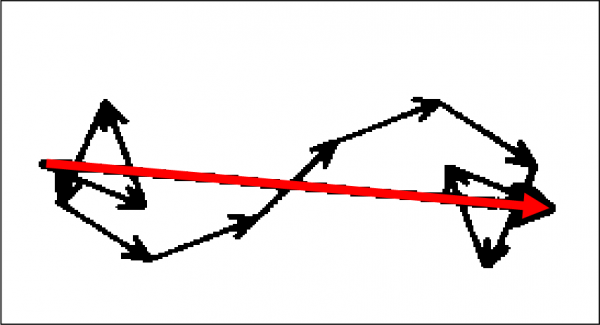
Attenzione, attenzione. Non concludiamo troppo frettolosamente! Finora abbiamo sempre detto che il tragitto percorso nel tempo minore è anche il tragitto di minima distanza. Vale ancora questa relazione? Siamo costretti a dire di NO. Questa uguaglianza vale solo nel caso che la velocità del cronometro sia sempre la stessa. Nella riflessione ciò è vero: l’intero percorso viene effettuato nell’aria, ossia in uno stesso tipo di “materiale” (lo specchio viene solo toccato…). Adesso, invece, il percorso viene effettuato parte nell’aria e parte nell’acqua. Dobbiamo accettare che cambi la velocità del cronometro nel completare il suo ciclo probabilistico. In altre parole, sembra proprio che la velocità della luce sia diversa. Non preoccupatevi. Non ci lasciamo convincere da parole e basta. Tra non molto descriveremo anche questo fatto! Per adesso accettiamo che il percorso minore non coincida con il tempo minore. A noi, però, interessa quest’ultimo, perché è proprio lui che comanda la direzione costante della lancetta. Ciò non capita dove il percorso é minimo, ma dove è minimo il tempo di percorrenza (è il cronometro che fa girare la lancetta). Scusate le ripetizioni, ma il concetto è troppo importante per non farlo nostro.
Per comprenderlo ancora meglio, facciamo un esempio veramente “estivo” in Fig. 28: tutti al mare, tutti al mare... Siamo in una spiaggia famosa e intasata (proprio ciò che io detesto, pazienza…), in cui vigila dalla sua torretta un bagnino B. In mezzo a tanta ressa, ecco che qualcuno o qualcuna (N) si spinge troppo al largo o, magari, ha avuto un crampo. La situazione può diventare tragica e il bagnino si lancia velocemente in acqua per effettuare il salvataggio. Anch’egli, come un fotone, ha davanti a sé molte possibilità.
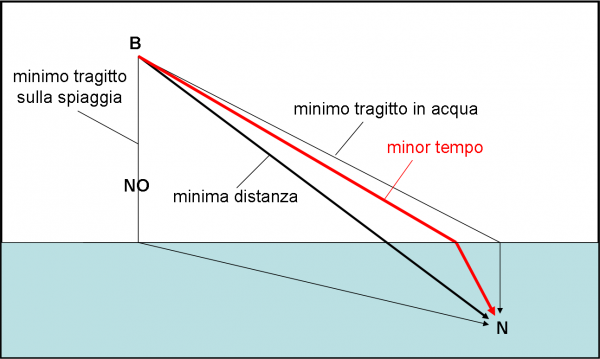
Di certo non sceglie una direzione opposta al mare! Tuttavia, la decisione non è del tutto banale. Anche se lui è un ottimo nuotatore sa benissimo che corre più velocemente di quanto non nuoti. Anch’egli è costretto a rallentare una volta entrato in acqua. Quale percorso dovrebbe scegliere per raggiungere N? Sicuramente non va dritto verso il mare, dato che poi avrebbe un tratto di nuoto eccessivamente lungo. Le scelte si restringono a due possibilità più ragionevoli: o sceglie il percorso di distanza minima, il più corto “in linea d’aria”, ma con un tratto di nuotata abbastanza lungo oppure sceglie di ridurre al minimo il percorso da effettuare in acqua, anche se comporta un tragitto più lungo da fare a piedi (ma correndo va più veloce).
Possiamo già notare che molto dipende dalle capacità del bagnino: se è un gran corridore sceglie la seconda opzione, se , invece, è un fantastico nuotatore può scegliere la via più corta. O, magari, anche dalle condizioni del mare (quanto rallenta il cronometro). In ogni modo, la decisione rimane sempre compresa tra queste due possibilità. L’importante è che impieghi il minor tempo per soccorrere N. Ovviamente non possiamo pretendere che il bagnino si fermi a fare i calcoli e quindi lui sceglierà più rozzamente. Noi, invece, conoscendo le sue potenzialità e avendo misurato i tratti di spiaggia e di acqua, sappiamo calcolare esattamente (con la solita regola probabilistica della QED) il percorso che viene effettuato nel minor tempo possibile.
Esso sarà quello rosso, una specie di compromesso tra quello con meno acqua e quello di minore distanza. Notate che il tragitto più probabile, deciso dalla QED, ci mostra un fatto non certo sconosciuto: il fotone-bagnino cambia la propria direzione una volta entrato in acqua. Vi dice niente il fenomeno della rifrazione luminosa? La Natura, cari amici, segue le regole della QED e fa piegare il raggio in modo da salvare lo sfortunato bagnante. E tutto ciò, utilizzando solo e soltanto le regole probabilistiche della MQ.
Un piccolo esercizio
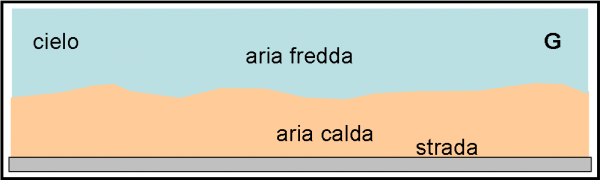
Si potrebbe considerare un altro fenomeno molto interessante, di cui avevo già abbondantemente parlato nelle “lezioni” di ottica (QUI). Parlo del “miraggio”. Esso si manifesta, ad esempio, quando si guida lungo una strada in una caldissima giornata di luglio e la strada appare come se fosse bagnata. In realtà, ciò che si vede è il … cielo. Noi pensiamo immediatamente che la strada sia bagnata, dato che “normalmente” si vede il cielo in terra solo quando vi è uno strato d’acqua che lo riflette parzialmente (leghiamo, più o meno inconsciamente, un effetto alla causa più “comune” che può averlo prodotto). Tuttavia, il cielo si riesce a vedere per terra anche quando la strada NON è bagnata e il fenomeno prende il nome di miraggio. Per risolvere il problema con la MQ, bisogna solo sapere che la luce viaggia più lentamente (il famoso cronometro) dove l’aria è più fredda e che il guidatore si trova in uno strato d’aria più fredda rispetto a quella vicinissima all’asfalto. Il discorso è esattamente lo stesso del bagnino… e lo lascio a voi. Divertitevi e mettete alla prova le capacità raggiunte nell’applicare la QED a fenomeni spiegabili con l’ottica geometrica. Per aiutarvi inserisco la Fig. 29 che rappresenta la situazione, con il guidatore posto in G.
Andare dritti conviene
Come vi avevo promesso, affrontiamo, ora, il problema del tragitto rettilineo della luce. Sembrerebbe un “atto di fede” e, invece, la QED non ha problemi a spiegare che è un risultato spiegabilissimo (con le sue regole). In altre parole, dimostriamo perché possiamo tranquillamente utilizzare percorsi rettilinei dei fotoni in qualsiasi mezzo stiano viaggiando.
Cosa ci dice la visione altamente democratica della QED? Un fotone è libero di andare dove vuole e come vuole. La probabilità di ciascuna di queste “scelte” è sempre la stessa. Esso può benissimo muoversi attraverso linee curve e strane quanto volete. Disegniamo la Fig. 30. Consideriamo dapprima le linee continue che uniscono la sorgente S e il rivelatore R. Non abbiamo niente tra di loro, solo un mezzo. Come dicevo, tutte e tre le linee hanno la stessa probabilità di essere percorse. Tuttavia, noi siamo interessati a sapere qual è quella che viene veramente scelta. I fotoni sono liberi, ma non … stupidi!
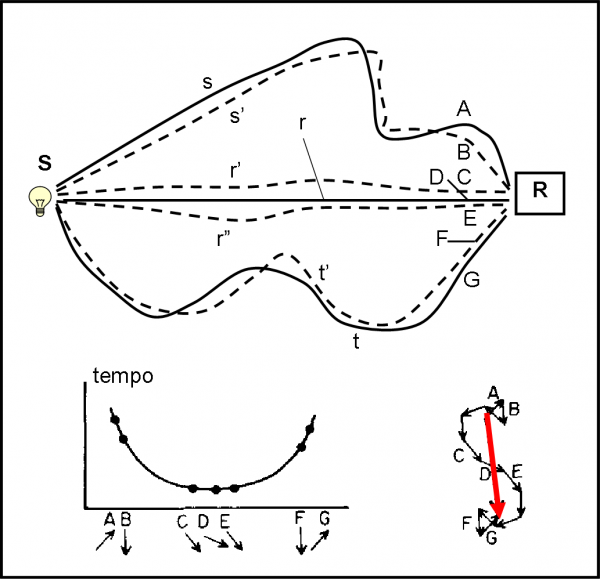
Immaginiamo, quindi, che i tragitti abbiano uno scambio di pensieri e di idee con quelli a loro più vicini. Anzi, è meglio dire che ogni traiettoria possibile tiene sotto controllo quelle vicine. Queste ultime siano rappresentate dalle linee tratteggiate. A questo punto è “ovvio” introdurre la solita regola della combinazione di ampiezze di probabilità. Se è vero che le strane traiettorie s e t hanno vicino delle altrettanto strane traiettorie s’ e t’ che differiscono di poco da loro, è anche vero che le traiettorie r’ e r’’ differiscono molto meno dalla traiettoria rettilinea r.
Il tempo impiegato a percorrere le varie traiettorie segue perfettamente quanto fatto finora per la riflessione e rifrazione. Se disegniamo il grafico tempo-posizione del percorso otteniamo la solita “parabola” che ben conosciamo. Come posizione, possiamo tranquillamente prendere quella misurata lungo una qualsiasi retta verticale che taglia le linee. Come le altre volte, ciò che conta è, però, che per traiettorie molto elaborate e decisamente più lunghe, una leggerissima variazione comporta, alla fine, una differenza di tempo impiegato significativamente diverso da quello della traiettoria vicina di casa.
Cosa vuol dire questa constatazione? Dovrete ormai saperlo molto bene: la lancetta del cronometro forma un angolo decisamente grande con quella vicina (siamo nella parte alta della parabola). Se invece consideriamo linee che si avvicinano al minimo percorso (quello rettilineo) le differenze in direzione della lancetta si fanno piccolissime, dato che i tempi per effettuare questi tragitti sono praticamente uguali. Non ci resta allora che combinare le frecce relative a tutti i tragitti per avere la solita conferma: le frecce lontane dal tragitto minimo si attorcigliano e la loro combinazione non porta a niente. Solo quelle vicino alla traiettoria rettilinea si sommano in modo costruttivo. La massima probabilità totale è merito loro, ossia sono proprio loro a descriverla e renderla alta. La probabilità massima si ha scegliendo una traiettoria rettilinea.
E’ importante notare ancora una volta (se ce ne fosse bisogno) che non è la probabilità della singola traiettoria (anche se è quella perfettamente rettilinea) a decidere il percorso di massima probabilità che ha la luce per andare da S a R, ma solo e soltanto l’insieme di molti percorsi talmente simili da far sì che le loro ampiezze si sommino effettivamente, raggiungendo tutte assieme un valore decisamente più alto di quelle frecce che perdono il loro tempo girando in tondo senza concludere niente.
Permettetemi un’analogia un po’ azzardata: è come se il fotone che va in linea retta “odorasse” le traiettorie vicine (come se fossero percorse anch'esse da fotoni "virtuali") e si muovesse all’interno di una piccola fascia di amici, stando bene attento a non allontanarsi troppo da loro. L’unione fa la forza! Possiamo, perciò, concludere che la luce NON va in linea retta per chissà quale strana legge fisica, ma solo perché è la traiettoria che le permette di combinare nel modo migliore e più redditizio le frecce vicine. E’ lo stesso identico risultato che avevamo trovato per la riflessione!
Vicini amichevoli, ma non troppo pochi
Un’ulteriore constatazione che ci verrà estremamente utile tra poco. Affinché l’unione di frecce con la stessa direzione faccia sentire il suo “peso” probabilistico, e necessario che la traiettoria abbia attorno a sé un numero sufficiente di amici, ossia di frecce da sommare. Se lo specchio, ad esempio, fosse troppo piccolo, la probabilità totale che riesce a formarsi potrebbe non differire molto dalla probabilità finale di un gruppo di traiettorie completamente strambe, ma molto vicine tra loro. Insomma, lo specchio non funzionerebbe molto bene e ben poca luce raggiungerebbe il rivelatore.
Tuttavia, dovremmo cambiare la conclusione che siamo abituati a trarre nella vita normale. Invece di dire: “Lo specchio è troppo piccolo e non riesce a riflettere” si deve dire: “Il fascio di traiettorie che colpisce lo specchio non riesce a costruire una probabilità finale di ampiezza sufficiente a superare quella di altri fasci vicini diretti in direzioni qualsiasi”. Pensateci bene e noterete una differenza sostanziale!
Quello che vale per uno specchio, però, vale anche per il suo esatto contrario (o quasi): un foro in cui la luce può passare tranquillamente.
Questo facile esperimento, che può diventare veramente importante, lo studieremo in dettaglio la prossima volta, dove toccheremo -senza nemmeno volerlo- il principio di indeterminazione di Heisenberg. Anzi, ci renderemo conto che lavorando con la QED diventa un’ovvia conclusione, di cui si può anche fare a meno… Si fa per dire, ovviamente…
Una considerazione abbastanza importante. Non è assolutamente vero che i fotoni che rimbalzano sul primo specchio devono sapere cosa fanno quelli del secondo specchio. Basta ragionare in termini di probabilità finale (ossia con le regole della QED) e tutto diventa logico. In parole semplicissime: ciò che noi vediamo come fenomeno fisico non è altro che un gioco eseguito da traiettorie che camminano vicinissimi tra loro. Il fenomeno SEMBRA avvenire in un solo modo, ma è più vero dire che il fenomeno avviene dove la probabilità è massima, seguendo regole perfette e perfettamente descrivibili. Vi stupirete di come sarà semplice descrivere una lente…
Cominciamo, però, a pensare alle assurdità che stanno scomparendo come neve al Sole.






19 commenti
Caro Enzo, che bella spiegazione!
Prima di passare al test che proponi, vorrei fare alcune considerazioni per vedere se ho davvero afferrato i concetti.
Prima di questo articolo le frecce delle probabilità erano in funzione della distanza da percorrere, poiché la velocità si presumeva uguale (dunque a percorso più breve corrispondeva un tempo di percorrenza più breve e viceversa).
Ora questa eguaglianza viene meno, poiché il tempo di percorrenza del tragitto non coincide più con la lunghezza del percorso (potremmo dire che la velocità non è più costante, ma che un mezzo più denso rallenta la velocità).
Dunque, ora conta solo se ci si mette meno tempo o si ci mette più tempo per giungere dalla sorgente al rilevatore.
Vorrei provare anch'io ad usare una racconto metaforico (sole per vedere se ho capito).
In un antico villaggio di montagna, un giorno arriva uno scalatore ipertecnologico, armato di mappe, telefono satellitare e quant'altro.
L'ingenuo visitatore sfida gli abitanti del villaggio a raggiungere la vetta nel tempo minore possibile. E gli abitanti sorridono.
Lui traccia una linea retta che unisce il villaggio alla vetta (la tecnologia non può far nulla contro l'ignoranza), sicuro che quello sia il percorso più breve.
Gli abitanti del villaggio, conoscono gli infiniti sentieri che conducono alla vetta e decidono di seguirne diversi, giusto per dare un piccolo vantaggio all'ignaro visitatore.
Ebbene nonostante lo sfoggio di tecnologia, anche l'ultimo degli abitanti, una volta arrivato sulla vetta tende una mano all'ipertecnologico visitatore per aiutarlo a raggiungere la vetta.
Eppure era il percorso più breve! Peccato che le amate carte non riportavano l'ubicazione dei rovi, delle rocce, e degli ostacoli che avrebbe dovuto superare, cosa che invece i sorridenti abitanti del villaggio conoscevano assai bene.
Una domanda mi sorge spontanea: il nostro fotone sembra già possedere la saggezza del villaggio, ossia sembra conoscere tutti i percorsi possibili, prima di effettuare la sua scelta “ponderata” (poi si sa che ci sono anche fotoni ostinati che seguono scelte diverse da quelle più comode, in fin dei conti anche a loro, prima o poi, va concessa una possibilità).
Ho provato partendo da questi presupposti (sgombrando la mente da indici di rifrazione, o angoli di riflessione, che non ho considerato minimamente) a svolgere il piccolo esercizio che hai proposto (ho usato Photoshop, giocherellandoci con pochi strumenti, poichè disegno malissimo), considerando alcune tra le tante possibilità di scelta, solo in funzione del presunto tempo impiegato per raggiungere il guidatore.
Nella figura sottostante ho provato a tracciare 4 diverse traiettorie:
http://www.astrobin.com/full/108209/J/
la linea nera rappresenta il percorso più breve in termini di distanza da percorrere;
la linea verde rappresenta il percorso più comodo, ossia quello che avviene per la maggior parte nella meno densa aria calda;
la linea gialla rappresenta il percorso che probabilmente permette al fotone di raggiungere l'automobilista nel più breve tempo possibile, considerando distanza e ostacoli (quantità di percorso in cui si deve attraversare l'aria fredda);
l'ultima linea, è rossa (nelle parti in cui attraversa l'aria fredda) e blu nelle parti in cui attraversa l'aria calda (ho voluto considerare anche una situazione in cui i raggi solari non sono perpendicolari al terreno, ma obliqui) e rappresenta il percorso più beve con raggi solari obliqui rispetto al terreno.
La figura sottostante mostra le stessa situazione di prima, cambia che è solo una porzione di strada che “riflette” il cielo e non tutta la strada.
http://www.astrobin.com/full/108209/K/
Prima di porre alcune domande, penso sia necessario verificare se ho compreso bene ciò che accade, oppure no, a partire dalla soluzione proposta (è corretta? È errata?).
Paolo
caro Paolo,
complimenti e grazie per la partecipazione!
1) perfetto riguardo alla linea che impiega meno tempo: è il tempo che comanda il cronometro e quindi è giusto che la probabilità sia massima dove si impiega meno tempo, dato che è proprio lì che siamo al minimo della curva e le variazioni della direzione delle frecce è molto piccola, ossia le frecce vicine si combinano costruttivamente.
2) Va benissimo l'esempio, dato che lo scalatore straniero percorre un tragitto più dispendioso come tempo. Ha fatto come il bagnino che si è gettato subito in acqua e poi ha dovuto nuotare troppo a lungo, oppure (per seguire il tuo esempio) che ha scelto la linea diretta.
3)Ti consiglio di cercare di non vedere il fotone che sceglie una strada, ma rimanere attaccato al concetto che il fotone segue qualsiasi strada, ma l'ampiezza di probabilità associata a certi tragitti porta alla probabilità finale più alta. Non voglio fare il pignolo, ma bisogna digerire bene il concetto che non è associata una freccia di probabilità al fotone, ma alle sue possibili traiettorie. Ecco perché parlavo di fotoni virtuali... Quando parte la luce, un fotone è dappertutto e vi sono tante frecce che segnano la probabilità di raggiungere la meta. Ovviamente, alla fine, la combinazione delle ampiezze dice quale è il percorso che è seguito preferibilmente. E' una differenza quasi impercettibile, ma che potrebbe complicare le cose quando si arriva all'interferenza e alla doppia fenditura... Comunque ci torneremo ancora sopra...
4) Riguardo all'esercizio, quello che hai fatto è un di più. Tu hai già risposto in anticipo... dicendo che la traiettoria più probabile è quella che impiega meno tempo e quindi è meglio che penetri, per quanto possibile, dentro all'aria calda dove il cronometro va molto più veloce ...
Tieni presente che la luce del cielo NON è obbligata a riflettersi sulla strada. Nessuno l'ha imposto e quindi può benissimo andare direttamente fino al guidatore senza abbassarsi verso la strada. Tuttavia, la zona calda sopra la strada offre possibilità di impiegare un tempo minore anche se la linea non è rettilinea. Non hai bisogno di riflessione, ma solo di entrare dentro... l'acqua, almeno per un po'. Ricorda sempre di definire bene l'evento che si vuole descrivere. In questo caso l'evento è: partire dal cielo e arrivare al guidatore. Non c'è bisogno di inserire una riflessione...
La risposta è molto più semplice e i percorsi più costruttivi non devono per forza toccare la strada... Non bisogna nuotare troppo anche se si è ottimi nuotatori. Meglio scegliere una via di mezzo... ma tra la linea retta e corta e una più lunga ma più veloce. Tuttavia, l'aria calda sveltisce il cronometro, ma non si può nemmeno esagerare con lo spazio percorso.
Anche i tuoi alpinisti locali, pur andando molto meglio sui sentieri che non su una parete verticale o tra rovi e cespugli, non possono permettersi di prendere strade troppo lunghe: Sentieri sì, ma non autostrade !
Comunque, sei perfettamente in sintonia!!!!
caro Paolo,
aggiungo un paio di considerazioni per non crearti inutili confusioni e per aiutarti un po'...
1) Ho parlato di cielo e non di Sole, che è qualcosa di limitato e posto in una certa posizione. In altre parole, qualsiasi parte di cielo può fare il giochino che vogliamo.
2) La riflessione che hai studiato tu andrebbe bene nel caso ci fosse dell'acqua sulla strada. Qui non c'è e quindi conta solo la rifrazione... Devi cambiare le tue linee per simulare il bagnino... Con l'acqua non sarebbe più un... miraggio ma una riflessione pura e semplice.
Spero, comunque, che la QED non rimanga una discussione fra noi due

Speriamo sia solo questione di ferie... Comunque è meglio che rallenti un po' l'uscita degli articoli e che poi faccia una bella e lunga sosta prima di passare veramente alla materia e agli elettroni, i grandi compagni di gioco dei fotoni...
Spero di aver capito come fare il disegno, vediamo se così va meglio
http://www.astrobin.com/full/108209/M/
In questo caso le linee gialla e rossa rappresentano quelle dove il tempo di percorrenza è minore, la linea nera il percorso più breve ma più impervio (tutto il tratto è nell'aria fredda), quella verde il percorso più lungo ma meno irto di ostacoli (quasi tutto nell'aria calda). Il blu è una via di mezzo fra nero e giallo, mentre il viola rappresenta uno dei possibili percorsi casuali, più lungo e con scarsi vantaggi rispetto agli altri.
Quindi l'ampiezza di probabilità sarà più elevata in prossimità dei possibili percorsi gialli e verdi (minor tempo impiegato), lì le frecce dovrebbero mantenere una direzione simile, per cui le probabilità si ampliano, mentre il percorso viola probabilmente sarà caratterizzato da frecce che assumo direzioni diverse, per cui le probabilità dovrebbero tendere ad annullarsi a vicenda.
Paolo
caro Paolo,
Direi che la conclusione è giusta. Tuttavia non è necessario, in questo caso, disegnare molte traiettorie come fai tu. Prendi due punti nel cielo, uno piuttosto alto (1) e uno piuttosto basso (2), vicino all'aria calda. L'evento è sempre dello stesso tipo: raggiungere G partendo da (1) o da (2). Tuttavia, le soluzioni sono diverse e quindi separiamo i due eventi: da (1) a G e da (2) a G. La traiettoria migliore per (1) continua a essere la linea retta nell'aria fredda, dato che qualsiasi curva o percorso che vada a finire nell'aria calda (puoi disegnarla come vuoi piegando all'inizio, alla fine o in mezzo), è sempre decisamente più lunga (temporalmente) da percorrere: quello che si guadagna quando finalmente si può viaggiare nell'aria calda si perde per il tempo impiegato a raggiungerla e a uscirne. (1) ha la massima probabilità di raggiungere G andando dritto e il cielo (1) si vede dov'è.
(2), invece, è talmente vicino all'aria calda che alla traiettoria conviene fare un passetto verso il basso e viaggiare nell'aria calda. Pensa a una traiettoria curvilinea che parte da (2) scende verso l'aria calda e poi lentamente torna verso G (su G deve arrivare per forza). Se teniamo conto che, inoltre, l'aria è sempre più calda andando verso il basso, la traiettoria che impiega meno tempo è proprio una specie di parabola che parte da (2) scende dentro all'aria calda e poi risale verso G. La luce di (2) arriva in G "dal basso" (con la traiettoria più probabile) e quindi sembra che il cielo sia sulla strada.
Poiché la nostra mente associa un riflesso del cielo a uno specchio o a una superficie bagnata, ecco che diciamo che ci sembra di vedere una strada bagnata, mentre quello che vediamo è il cielo di (2) che ha seguito la traiettoria più breve (come tempo) e quindi anche più probabile.
A questo punto possiamo dire che di cento fotoni che partono da (2) una buona parte raggiunge G seguendo la linea curva... mentre di cento fotoni che partono da (1) la maggior parte raggiunge G lungo la linea retta.
OK?
Una situazione cosi ?
http://www.astrobin.com/full/108209/N/
Dove per coprire la traiettoria tracciata in rosso dal punto 1 fino all'automobilista (nonostante sfrutta per buona parte del percorso l'aria calda e molto calda, risulta troppo lunga) serve più tempo della traiettoria diretta (linea nera).
Al contrario, la traiettoria verde dal punto 2, riesce ad esser leggermente più veloce di quella diretta, sfruttando l'aria calda e molto calda.
Spero che così vada meglio e lascio spazio ad altri che spero intervengano.
Paolo
caro Paolo,


so che non dovrei (per lasciare spazio anche ad altri) ma non posso farne a meno: PERFETTO!!!!!!
Penso che tra un po' ti divertirai parecchio con la QED e ... salutami il cappellaio matto, ormai sei uno degli amici di Alice (nel senso buono ovviamente!)
Ciao Enzo,
per questioni di tempo mi limito a leggere gli articoli per cui chiedo scusa se l'argomento è già stato trattato.
Ho capito che abbiamo un cronometro e che lo facciamo partire quando il fotone parte dalla sorgente e lo fermiamo quando arriva al rilevatore.
quello che non mi è chiaro è come faccio a determinare per ogni percorso la direzione della freccia quando "si stoppa" il cronometro.
Esiste un metodo?
caro Piero,
la freccia gira con il cronometro e quindi quando si ferma il cronometro la direzione è proprio quella della lancetta.
ciao enzo.
forse non sono stato troppo chiaro. quello che non capisco è come faccio a stabilire quando si deve fermarare il cronometro e quindi stabilire dove punta la freccia. per esempio nel caso della riflessione non capisco come si faccia a stabilire che i percorsi più lontani hanno le frecce che praticamente danno contributo nullo. lo devo prendere come un dato di fatto o esiste un procedimento?
caro Pietro,
lo stabilisce la curva tempo-posizione. E' una questione di pura geometria (quando siamo nell'aria): due percorsi lunghi che finiscono vicini nello specchio hanno una differenza di lunghezza tale da permettere alla freccia di girare sensibilmente tra uno e l'altro. Intorno al punto di mezzo, invece, due percorsi che finiscono in due punti vicini hanno percorsi quasi uguali e la freccia si è spostata di pochissimo da uno all'altro. E' una caratteristica della parabola o di curve simili: più si va lontani dal vertice e più, a parità di dx, aumenta dy. Il contributo nullo significa proprio che frecce vicine, ma che hanno fatto percorsi lunghi, sono orientate con angoli molto diversi tra loro. Tutto lì...
Ciao Enzo, sto seguendo con passione questa serie di articoli e le risposte che dai a Paolo mi aiutano a mettere a fuoco alcuni dubbi.
sto seguendo con passione questa serie di articoli e le risposte che dai a Paolo mi aiutano a mettere a fuoco alcuni dubbi.
Mi permetto solo di dire che non e' assolutamente una questione tra te e Paolo
Quando leggo questi articoli ripenso spesso alle tue riflessioni sulla MQ e "Dio" e alla grandezza della Natura.. Approfondire questi concetti ci fa davvero entrare in sintonia con il Tutto ...qualsiasi cosa esso sia ;)
grazie Zeneize...
lo immaginavo, ovviamente, ma vorrei istigare a sollevare ogni dubbio senza paura, dato che quando si affrontano i diagrammi di Feynman bisogna aver digerito perfettamente le regole e soprattutto essere entrati nel nuovo mondo. I principi fondamentali devono essere chiari...
certo che spiegato cosi mi sono trovato molto meglio rispetto alla spiegazione in astronomia.com fatta qualche tempo fa, grazie mille...
E grazie mille anche a Paolo per il contributo con l'esercizio, mi ero fatto un'idea simile ma non ne ero per niente sicuro!
riflettevo ancora sull'articolo e l'esercizietto...
Mi è venuto un dubbio, ma se il tempo di percorrenza della luce varia al variare del mezzo, o della temperatura del mezzo, vuol dire in sostanza che varia la sua velocità.
Conseguentemente non è folle ritenere che la velocità della luce nell'universo primordiale sia stata più veloce di quella di adesso, ai tempi l'universo era molto più caldo...
Dove sbaglio?
beh... Ale, sappiamo benissimo che la velocità della luce diminuisce attraversando un mezzo. Quella massima è nel vuoto, dove caldo e freddo non hanno senso. L'esercizietto si riferisce all'aria che certo vuoto non è...
Tuttavia, se riuscirò ad andare fino alla fine della QED vedremo che non vi è nessun problema ad andare più veloci della luce e verso il passato, su spazi e tempi molto piccoli.
Buongiorno,
sto leggendo QED di Feynman ma devo dire che senza il supporto di questi vostri articoli che seguono passo passo il libro non riuscirei a venirne a capo.
Però... c'è un però... anche qui sul vostro blog trovo una cosa che non capisco e quindi ho pensato di porvi questa domanda.
Faccio riferimento alla figura 30 dell'articolo "Feynman e la QED. 5: un bagnino esperto e degli ottimi vicini di casa" il cui link è
http://www.infinitoteatrodelcosmo.it/2014/07/27/feynman-e-la-qed-5-un-bagnino-esperto-e-degli-ottimi-vicini-di-casa/
(l'articolo qui sopra se leggete questo commento nel punto in cui l'ho lasciato)
La frase che vorrei discutere è la seguente:
"Se è vero che le strane traiettorie s e t hanno vicino delle altrettanto strane traiettorie s’ e t’ che differiscono di poco da loro, è anche vero che le traiettorie r’ e r’’ differiscono molto meno dalla traiettoria rettilinea r".
In sostanza, per come l'ho capita io, siccome le traiettorie più o meno rettilinee differiscono tra loro (per quanto riguarda lo spazio percorso dal fotone) meno di quanto differiscono tra loro le traiettorie "strane", le prime sono rappresentate da frecce che si sommano e quindi aumentano la probabilità di essere quelle più seguite dai fotoni mentre le traiettorie "strane", in virtù della loro maggiore differenza tra le loro lunghezze, sono rappresentate da frecce che si elidono (quasi) a vicenda e quindi diminuiscono la loro probabilità di essere quelle più seguite.
Io però penso si possa dire che per qualsiasi traiettoria t (vale sia per quelle "strane" che per quelle quasi rettilinee) è possibile immaginare una traiettoria t' la cui lunghezza differisca da t di un valore "epsilon" piccolo a piacere. Se così non fosse vorrebbe dire che lo spazio delle possibili traiettorie avrebbe dei "buchi", non sarebbe continuo.
Ma se è così allora per qualunque traiettoria (che sia "strana" o quasi rettilinea) esiste un gruppo di traiettorie di lunghezza così vicina alla sua che le frecce da queste rappresentate si sommano a quella della traiettoria data, invece di elidersi.
Ovvero (2) che la traiettoria rettilinea non è l'unica che abbia delle vicine così "amiche" da collaborare con lei nell'essere tra quelle con la probabilità più alta di essere scelte dai fotoni ma che queste traiettorie "gentili" le hanno tutte le traiettorie e quindi che tutte le traiettorie fanno parte di un gruppo che ha un'alta probabilità di essere scelto da un fotone.
Ovvero (3), se per ogni traiettoria esistono infinite traiettorie che differiscano da lei per un valore "epsilon" piccolo a piacere, allora di ogni traiettoria immaginabile possiamo dire che ne esistono altre "talmente simili da far sì che le loro ampiezze si sommino" (cito dall'articolo) non solo dei percorsi vicini alla traiettoria rettilinea.
Spero di essere stato chiaro nella mia esposizione.
La domanda è: posto che effettivamente la luce sembra muoversi secondo quanto indicato dalla QED, ovvero che effettivamente sembra prediligere le traiettorie vicine a quella rettilinea, dov'è l'errore nel mio ragionamento?
Un cordiale saluto e un ringraziamento per l'aiuto che mi state dando a capirci qualcosa in questa teoria.
Massimiliano
caro Massimiliano,
purtroppo sto passando un periodo difficile e non ho tempo per commentare nel modo voluto. In linea di massima ti posso dire che bisogna pensare anche al tempo minimo. Nello scambio di commenti avuti con Paolo puoi forse trovare maggiore aiuto. Magari, se avesse tempo, lo stesso Paolo potrebbe seguirti meglio in questo frangente... Chiedo scusa, ma anche tanta pazienza nei miei confronti.
Caro Vincenzo non scusarti, ti auguro di metterti presto alle spalle questo brutto periodo che stai passando.
Un caro saluto, anche se non ci conosciamo.