Abbiamo imparato a calcolare la probabilità di un evento che può verificarsi attraverso varie vie alternative. Come? Tracciando per ogni possibile percorso una freccia (secondo certe regole) e “sommandole” vettorialmente, in modo da ottenere una freccia finale. La freccia è stata chiamata ampiezza di probabilità e il suo quadrato è proprio la probabilità che l’evento si verifichi. Attenzione: abbiamo considerato tutte le vie possibili che un fotone può seguire, partendo da una sorgente S e raggiungendo un rivelatore R. Ripeto ancora: sono traiettorie alternative, indipendenti l’una dall’altra, che, però, finiscono nello stesso punto, o -meglio ancora- che soddisfano l'evento.

In questo modo, abbiamo considerato ogni possibile percorso della luce senza alcun favoritismo o preconcetto sul risultato finale (sia che lo conosciamo o no attraverso la realtà quotidiana). Solo la freccia finale ci dice con quale probabilità l’evento può avvenire e quali sono i percorsi che contribuiscono in modo preponderante alla sua riuscita. Possiamo, allora, concludere che questa è la strada che il fotone percorre con maggiore probabilità.

Abbiamo visto che, in molti casi, il percorso che dà la massima probabilità di riuscita è quello di durata minima. Se l’evento avviene con la luce che attraversa solo un mezzo (aria, ad esempio), il percorso di minima durata è anche quello di minima distanza. Nel caso della riflessione semplice, ad esempio, questo percorso è quello di un fotone che rimbalza con un angolo di incidenza uguale all’angolo di riflessione, proprio come ci mostra la realtà di tutti i giorni. In realtà, sarebbe meglio dire che le traiettorie più probabili sono quelle che stanno abbastanza vicine a questa configurazione.

Le cose cambiano un po’ con la rifrazione e il percorso più probabile è sempre quello in cui si impiega il minor tempo, ma non coincide con quello di minima distanza (spaziale), dato che i fotoni devono passare da un mezzo (aria) a un altro (acqua o vetro).

Sfruttando questa caratteristica della luce, siamo anche riusciti a far arrivare su un unico punto, e con la stessa probabilità, tutte le traiettorie che in aria avrebbero impiegato tempi diversi. E’ bastato inserire un pezzo di vetro sagomato (lente) in modo che il tempo finale impiegato da un fotone fosse sempre lo stesso, indipendentemente dal punto del vetro colpito. Il fotone può toccarlo in qualsiasi punto, ma converge sempre sul fuoco contribuendo alla probabilità finale nello stesso identico modo che avrebbe fatto se avesse seguito il percorso più corto. Un risultato che conosciamo molto bene nel mondo comune e che viene usato per la costruzione dei cannocchiali e dei telescopi.

Ci siamo, però, anche accorti che se limitiamo troppo il fascio di traiettorie percorribili, può accadere che traiettorie più dispendiose in termini di tempo e distanza abbiano la stessa probabilità di essere seguite da un fotone, di quelle favorite intuitivamente (minima distanza e tempo). Un risultato contro intuitivo nella vita di tutti i giorni, ma che descrive, senza nemmeno averlo cercato, nientemeno che il principio di indeterminazione di Heisenberg. Non solo però… i più preparati possono vedere in questo risultato il punto di partenza per ottenere il celebre esperimento della doppia fenditura, proprio quello che dà la migliore rappresentazione dell’assurdità e della genialità dell’intera MQ. Potete anche provare a ottenerlo da soli, dato che tra non molto ci arriveremo con grande scioltezza.

A questo punto, possiamo eseguire (quando  diventa utile per non creare troppa confusione) una semplificazione che ormai ci possiamo permettere: consideriamo come traiettoria seguita dalla luce solo quella che dà il massimo contributo alla probabilità che l’evento si verifichi. Questa è, quasi sempre, proprio la traiettoria descritta normalmente dall’ottica geometrica. Non ditemi: “Ma allora perché abbiamo fatto tanta fatica e usato tanti artifici incomprensibili e solo calcolabili e non comprensibili?”. La ragione è una e una sola: trattare TUTTI i fenomeni legati alla luce e alla sua interazione con la materia è possibile solo attraverso una visione puramente probabilistica, perfettamente quantificabile, ossia attraverso la QED. Noi stiamo applicandola a fenomeni semplici e abbastanza intuitivi, ma la sua unicità diventa ben più visibile solo quando le difficoltà aumentano. Senza dimenticare, poi, la strana doppia natura della luce, che solo la MQ e la QED riescono a descrivere senza cadere nella pazzia. Forse, proprio perché sono teorie “pazze” e assurde per definizione…

Semplifichiamo

Torniamo a noi e descriviamo meglio cosa stiamo per iniziare a fare. Vogliamo studiare eventi che possono essere scomposti in due o più eventi. In altre parole, vogliamo calcolare la probabilità finale di un certo evento attraverso le probabilità dei singoli sotto-eventi che lo costituiscono. Tanto per fare un esempio, che tratteremo in dettaglio, pensiamo alla semplice riflessione di uno specchio. Nei capitoli iniziali abbiamo considerato tutte le possibili traiettorie con la loro singola probabilità e poi siamo riusciti a trovare quelle che davano il massimo contributo alla probabilità finale. Adesso, invece, consideriamo la traiettoria come stabilita e vediamo come la probabilità si trasforma ad ogni singolo passo dell’intero fenomeno.

Dobbiamo essere sinceri. Questo procedimento è un po’ più complicato di quelli adottati finora. Complicato, però, non vuol dire maggiore difficoltà concettuale, ma solo possibile confusione nella serie di operazioni da svolgere. Niente di tragico, ma è necessaria molta attenzione e pazienza. Capiremo subito il perché della semplificazione di cui abbiamo appena parlato e che è meglio ribadire ancora per non creare ulteriore confusione.

Quando facciamo partire la luce da una sorgente sappiamo benissimo che essa può andare in ogni direzione e molte traiettorie giungono sullo specchio, ciascuna con la propria freccia. In altre parole, abbiamo una dispersione della luce e non certo un solo raggio luminoso. Tuttavia, solo uno (o meglio solo un certo gruppo abbastanza stretto, ma non troppo) raggiunge il rivelatore dando origine alla massima probabilità.  Possiamo permetterci di disegnare solo quello, come, in fondo, abbiamo fatto all’inizio di tutto con l’esperimento della doppia riflessione? Sì, perché, ripetiamo ancora, ormai sappiamo benissimo come calcolare questa traiettoria. Praticamente è come assumere che ogni fotone che parte dalla sorgente arriva sul rivelatore attraverso un solo percorso, quello più probabile. Ciò è quello che ci direbbe l’ottica geometrica, ma noi sappiamo che è invece un’approssimazione che ormai ci possiamo permettere.

Un dovuto riassunto preparatorio

Luce, fotoni, raggi luminosi. Facciamo, ancora una volta, un po’ di chiarezza sul concetto che stiamo seguendo e che può confondersi con uno molto simile. Quando, normalmente, pensiamo a una sorgente luminosa, non ci è difficile immaginare che la luce vada in ogni direzione. Disegniamo questa configurazione spesso e volentieri attraverso i raggi luminosi. Tuttavia, in questo caso, ogni raggio può essere considerato un fotone singolo, ossia una vera e propria particella. Noi, invece, facciamo una cosa concettualmente molto diversa (e fondamentale per la MQ). Lo possiamo fare, solo perché lavoriamo in termini di probabilità e non di realtà fisica. Quando diciamo che la luce parte da S e che ogni direzione è possibile, intendiamo che un singolo fotone può andare in ogni direzione, dato che non abbiamo modo di sapere la sua traiettoria. Solo alla fine, attraverso il calcolo delle probabilità, potremo dire quale è la più conveniente e probabile. Solo alla fine, ossia solo quando esso si comporta sicuramente come una singola particella, come ci dimostra il “tic” del rivelatore.

La conclusione può essere la stessa (prendere cento fotoni particelle e mandarle in molte direzioni o prendere un solo fotone di carattere ambiguo e tracciare le sue possibili direzioni), ma concettualmente la cosa è ben diversa e porta, alla fine, a una visione completamente diversa della Natura.

Nel primo caso diciamo che abbiamo tanti fotoni, ognuno su una direzione, e questa direzione può essere qualsiasi; nel secondo caso diciamo, invece, che il fotone, pur essendo una singola entità, può trovarsi ovunque! Nel primo caso facciamo fisica classica e leghiamo un’entità con un ben definito percorso, benché possa essere qualsiasi; nel secondo caso facciamo MQ in quanto ammettiamo che l’entità possa trovarsi ovunque, lungo qualsiasi direzione rispetto alla sorgente. Ecco perché mi sono permesso all’inizio di rappresentare questa “ubiquità” con l’idea delle particelle “virtuali”.

Capiamo, allora anche perché, nel primo caso siamo obbligati, per spiegare certi fenomeni, come l’interferenza, a sostituire il termine particella con il termine onda e accettare un bimodalità inquietante. Una situazione veramente assurda, ma senza via d’uscita, dato che il rivelatore ci dimostra che il fotone è una particella mentre l’interferenza ci dimostra che deve essere un’onda. Nel secondo caso, basta, invece, un'unica entità, capace di essere ovunque e di cambiare la propria natura al momento opportuno. In questa logica, la MQ è molto meno assurda della realtà!

Tanti passi per un solo risultato

Torniamo a noi con la  Fig. 35 e cominciamo, finalmente, con una descrizione del tutto generale del procedimento, proprio per meglio spiegare le operazioni da svolgere, che chiamiamo prodotto di frecce. Non entro nei dettagli, ma la parola ha un senso profondo perché si riallaccia proprio alla nascita di questa operazione fin dai tempi più antichi.

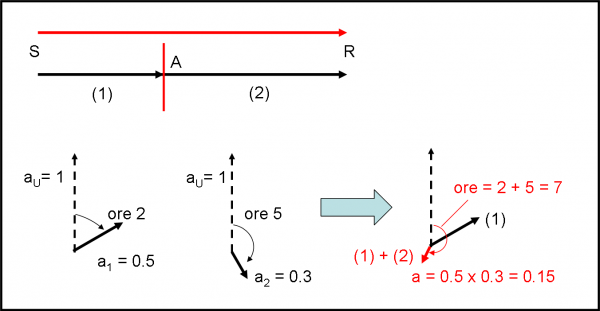
Consideriamo un evento che può essere scomposto in due eventi successivi (il numero, però, può essere qualsiasi). Ognuno di questi eventi ha una sua freccia di probabilità. Come poter passare dalla prima fino a quella conclusiva? Ecco il nostro problema. Disegniamo separatamente i due “passi” dell’evento, (1) e (2). Nel primo, la luce parte da una sorgente S e arriva fino a un certo punto A. Cosa succede durante il tragitto c’interessa poco, per il momento. Di sicuro la luce alla partenza ha una freccia di ampiezza UNITARIA con una direzione qualsiasi.

Scegliamo come direzione di partenza quella verticale, ossia con la lancetta del cronometro che indica mezzanotte. Questa è la posizione di angolo uguale a ZERO. Alla fine del primo tragitto ci dobbiamo aspettare che la freccia sia cambiata. Ha subito, infatti, due trasformazioni: un accorciamento e una rotazione. Questo fatto lo conosciamo benissimo. La freccia si accorcia perché la probabilità di arrivare fino ad A è minore di quella unitaria di  partenza (la luce può essersi riflessa, rifratta o qualsiasi cosa vogliate). La sua direzione è anche variata rispetto alla mezzanotte. Il cronometro, infatti, è partito subito e quando la luce arriva su A, la lancetta ha percorso un certo angolo. In basso disegniamo la freccia che si ottiene. Ad esempio, essa si è ridotta del 50% (in termini di unità vale, quindi, 0.5) e la sua direzione è quella delle ore 2 (60°).  La luce continua con il secondo passo e va da A a R. Assumiamo, a questo punto, che A sia una nuova sorgente e calcoliamo come la freccia unitaria si trasformi nel secondo passo dell’evento. Ad esempio, la freccia unitaria si è accorciata fino a diventare 0.3. Inoltre, il tempo impiegato per passare da A a R è stato più lungo di quello del primo passo e la lancetta (ossia la direzione della freccia) si è portata da mezzanotte fino alle ore 5. Anche questo risultato è riportato nella parte bassa della figura.

Ciò che vogliamo calcolare adesso, conoscendo le singole trasformazioni della freccia, è la trasformazione finale, ottenuta combinando in qualche modo le due trasformazioni. Questo procedimento non è altro che il prodotto delle frecce, ossia delle ampiezze di probabilità.

La prima freccia ha lunghezza 0.5 alla fine del primo passo. Questa lunghezza si è poi ulteriormente accorciata. Di quanto? Proprio del prodotto tra 0.5 e 0.3, ossia la sua lunghezza finale vale 0.5 x 0.3 = 0.15. Perché posso fare semplicemente il prodotto delle lunghezze? Proprio perché esso mi indica di quanto la lunghezza della prima freccia si è ulteriormente accorciata dopo il secondo passo. Se, infatti, il secondo passo ha ridotto la freccia unitaria fino a 0.3, ha ovviamente ridotto una freccia di ampiezza 0.5 a un’ampiezza di 0.5 x 0.3, ossia 0.15. Guardate che sto dicendo cose veramente elementari. Praticamente sto spiegando il prodotto di due numeri. Il secondo accorciamento che fa passare  da 1 a 0.3, fa passare da 0.5 a 0.15, che è il prodotto dei due accorciamenti.

Ancora più semplice è il calcolo della posizione della lancetta finale. Basta sommare le ore: 2 + 5 = 7. Infatti, la seconda trasformazione ha ruotato la freccia unitaria di 5 ore. Questo vuol dire che se la freccia ottenuta alla fine del primo passo era diretta verso le ore 2, l’orologio ha ancora percorso 5 ore prima di fermarsi definitivamente alle ore 7. Perché tutto questo “pasticcio”? Perché non cercare di semplificare la trattazione parlando solo di ciò che succede, di volta in volta, alla freccia dopo ciascun evento parziale? La ragione è semplice: per poter trattare ogni sotto-evento come evento scollegato dagli altri. Solo dopo, a seconda di ciò che vogliamo ottenere, possiamo eseguire la trasformazione completa. Il risultato finale della freccia, andando da S fino a R, è rappresentato nella parte destra della figura, dove vi sono sempre, in bell’evidenza, la freccia unitaria e la direzione di partenza

Non preoccupatevi se la faccenda vi è sembrata un po’ difficile. Adesso l’applicheremo a casi già trattati e i dubbi rimasti scompariranno. Comunque, questo processo di trasformazione è troppo importante e quindi, senza vergognarvi e senza curarvi di farmi troppe domande, chiedetemi tutti i chiarimenti per essere padroni di quanto ho cercato di descrivere. Ho cercato, infatti, di semplificare ancora di più quanto descritto da Feynman, ma non vorrei che due semplificazioni portino a una difficoltà maggiore (soprattutto se una delle due è la … mia!).

Posso, però, cercare di semplificare ancora (anche se va un po’ contro lo spirito guida). Ogni passo dell’evento complessivo porta a una freccia ridotta e ruotata. In pratica, basta considerare la freccia finale del primo passo, accorciarla di quanto dice in percentuale il secondo passo e continuare a far girare il cronometro. Idem con i passi successivi e alla fine si ottiene il risultato voluto. Insomma, accorciare, di volta in volta, una freccia, in base a quanto dice ogni singolo passaggio. Per la direzione della freccia, basta continuare a farla girare da dove era arrivata il passo prima. Insomma, scegliete il modo che preferite, ma tenete conto che l’importante è saper rendere indipendenti i singoli passaggi.

Riassumendo:

(a) Quando vogliamo calcolare la probabilità di un evento ottenibile con molte vie alternative bisogna sommare le frecce (ampiezze) di ogni via.

(b) Quando vogliamo calcolare la probabilità finale attraverso i vari passi di un evento, bisogna moltiplicare in successione le frecce (ampiezze) di ogni passo

Riflessione semplice

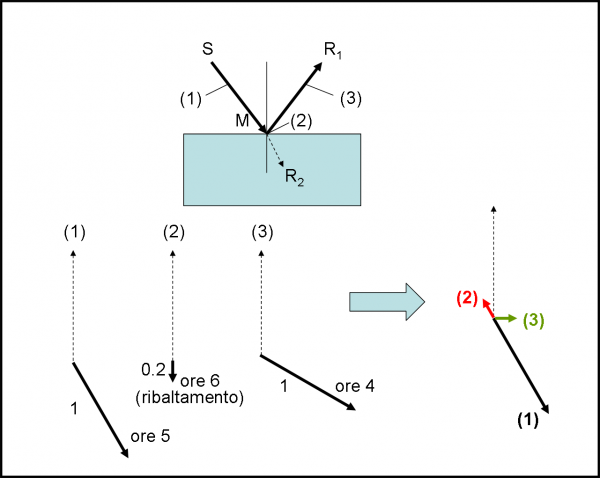
Prendiamo come esempio proprio l’evento forse più semplice trattato finora: la riflessione semplice. La “spezziamo”, nella Fig. 36,  in tre eventi singoli: 1) dalla sorgente allo specchio; 2) la riflessione; 3) dallo specchio fino al rilevatore R₁.

Voglio farvi notare che la riflessione in sé determina un  risultato che è legato al tipo di sostanza coinvolta (aria, vetro, acqua, ecc.). Per adesso accettiamo il risultato relativo senza chiederci “perché”. La motivazione la vedremo in seguito…

Il primo passo non comporta alcuna riduzione della lunghezza della freccia in quanto abbiamo assunto che tutti i fotoni che partono da S raggiungano R₁ o R₂ (una semplificazione che possiamo fare, dato che sappiamo bene come trattare le vie alternative) attraverso il percorso più probabile. La lancetta, però gira, dato che il tempo passa. Ad esempio, essa raggiunge le ore 5. Questo valore dipende solo e soltanto dalla distanza tra la sorgente e lo specchio.

Il secondo passo comporta (accettiamolo come un dato di fatto) una decisa riduzione di ampiezza che diventa 0.2. Accettiamo anche il risultato che la freccia faccia mezzo giro (si ribalti), ossia la lancetta segni le ore 6.

Il terzo passo è simile al primo: l’ampiezza non cambia, ma la lancetta potrebbe anche girare di più o di meno a seconda della distanza tra specchio e rivelatore R₁. Poniamo, ad esempio, che sia un po’ più corta e la lancetta del cronometro si fermi sulle 4.

Applichiamo la nuova regola di moltiplicazione e otteniamo che l’ampiezza finale è il prodotto delle tre ampiezze relative a ogni passo, ossia 1 x 0.2 x 1 = 0.2. La rotazione finale del cronometro è la somma delle rotazioni, quindi: 5 + 6 + 4 = 15 = 3. In pratica, è la somma dei due passi (1) e (3), a cui si aggiunge un capovolgimento del verso, dovuto alla riflessione aria-vetro.

L’ampiezza finale, quindi, vale 0.2 il che porta a una probabilità di 0.04, ossia il 4% della luce viene riflessa e raggiunge R₁. Il risultato è ovviamente uguale a quello che abbiamo descritto all’inizio delle lezioni.

Ricordiamoci sempre che tutte queste belle operazioni portano a risultati esatti delle probabilità finali, permettendoci di calcolarle con estrema precisione e, quindi, sapere come si comporta la Natura. Tuttavia, resta sempre incomprensibile il fatto che quattro fotoni su cento decidano di rimbalzare!

Nell’esempio precedente (riflessione semplice) possiamo anche seguire l’evento complementare, ossia quello che descrive la traiettoria che arriva fino al rivelatore R2, posto dentro al vetro. Anche questo è composto da tre passi: (1) tragitto sorgente-specchio; (2) passaggio attraverso la superficie del vetro; (3) tragitto, dentro al vetro, dalla superficie fino al rivelatore R₂. L’abbiamo rappresentato in Fig. 37.

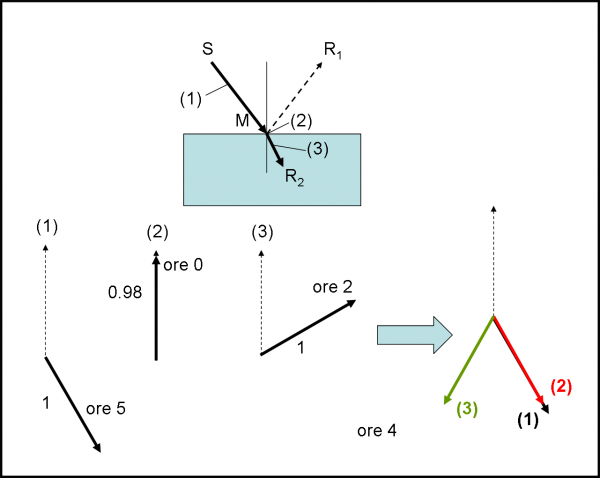
Il primo passo è identico a quello precedente, ossia ampiezza immutata e lancetta sulle ore 5. Il secondo passo causa una piccolissima riduzione della lunghezza della freccia unitaria portandola a 0.98. La lancetta, invece, non si muove. Il terzo passo è nuovamente analogo a quello della riflessione, ma avviene all’interno del vetro. La freccia unitaria resta quella che è e la lancetta gira, ad esempio, fino alle ore 2 (dipende essenzialmente da quanto è vicino il rivelatore alla superficie).

Il prodotto delle frecce ci dice che l’ampiezza finale è 1 x 0.98 x 1 = 0.98; la rotazione finale è 5 + 2 = 7.  La probabilità di questa strada complementare a quella della riflessione è, quindi, 0.98 ² = 0.96, ossia il 96%.

Non ci meravigliamo certo che la somma delle due probabilità sia proprio uguale al 100% (erano le sole due vie possibili). Attenzione, però, a non cercare di combinare le ampiezze dei due percorsi per ottenere quella finale del 100% con il metodo della somma dei vettori! Questo si può fare solo se le vie alternative portano allo stesso rilevatore e non a due diversi. Anzi, ancora meglio, le due vie non sono vie alternative di un solo evento, ma sono vie che si riferiscono a eventi del tutto diversi. Mi raccomando…

Fermiamoci qua, ma nella prossima lezione continueremo a esercitarci con la moltiplicazione delle frecce di probabilità, scomponendo gli eventi che già conosciamo in vari passi. Dobbiamo acquistare una grande dimestichezza: le frecce devono diventare come il pane quotidiano…