Per affrontare meglio questo concetto ci serve  un’ulteriore applicazione della moltiplicazione di ampiezze di probabilità (ossia le ben note frecce). Negli articoli precedenti abbiamo detto che questo procedimento si applica per descrivere come “evolve” la freccia di probabilità durante i passi successivi in cui può essere scomposto un evento.

Uno o l’altro per me pari sono

La regola della moltiplicazione si applica, però, anche a un evento che consiste di “cose” che accadono in concomitanza, indipendentemente tra loro e magari nello stesso momento.

Passiamo subito a un esempio: supponiamo di avere due sorgenti X e Y e due rivelatori A e B. Vogliamo calcolare la probabilità di un evento così definito: dopo che un fotone è uscito da X e uno da Y, sia A che B vengono raggiunti da un fotone. I due fotoni non si riflettono né attraversano qualche mezzo diverso. No, vanno senza problemi dove vogliono o -meglio- possono. Per studiare questo evento, che sembrerebbe di una banalità irrisoria, possiamo smettere di fare semplificazioni come quelle usate per la riflessione semplice o doppia, dove avevamo considerato solo una traiettoria, quella in qualche modo più probabile. Adesso, consideriamo veramente il fotone come un qualcosa che può andare ovunque (pur limitandoci alle linee rette, dato che sappiamo perché si può fare). Sembra una cosa semplice, ma finalmente affronteremo di petto la vera essenza del fotone e della QED. Un fotone esce da X e un fotone esce da Y, ma entrambi hanno a disposizione l’intero spazio e niente può disturbarli prima di arrivare (se arrivano) in A e B.

Se continuassimo a confondere una singola traiettoria con un singolo fotone, potremmo dire con grande sicurezza: l’evento capita sempre! Infatti, vi è sempre almeno un fotone che va da X ad A e uno che va da Y a B. L’errore di questo ragionamento è pensare che per ogni traiettoria esista un fotone. Invece, la situazione è ben diversa concettualmente: ogni traiettoria è un possibile percorso di un singolo fotone, ossia esso può trovarsi in una qualsiasi di esse, con una certa ampiezza di probabilità. In queste condizioni non è così sicuro che i due fotoni lanciati da X e Y debbano veramente arrivare su A e B o –quantomeno- molto dipende da “come” ci arrivano. In altre parole, studiamo la probabilità di arrivarci.

L’evento deve tener conto sia del fotone di X che di quello di Y. In altre parole, i fotoni che partono da X e Y non sono mai veramente indipendenti ai fini dell’evento. L’evento ci dice, in fatti, che sia il fotone di X sia quello di Y devono arrivare a destinazione e quindi è giusto e “logico” adottare la regola della moltiplicazione.

Spieghiamo meglio le cose attraverso la semplicissima Fig. 43. Prima di farlo, però, indichiamo con esattezza e senza alcuna semplificazione, cosa è necessario e sufficiente conoscere per rappresentare la luce che esce da una sorgente: (1) l’angolo della freccia segnato dalla lancetta del cronometro che gira in relazione al colore della luce; (2) la lunghezza della freccia che, però, dobbiamo considerare variabile NON perché incontra qualche ostacolo, ma solo perché percorre uno spazio crescente.

La seconda caratteristica ci è nuova, dato che finora non aveva importanza per i fenomeni studiati. Per essere pronti a entrare nel mondo della materia, però, non possiamo più trascurarla. In particolare, la lunghezza della freccia, ossia l’ampiezza della probabilità che il fotone ha di viaggiare su quella traiettoria, è inversamente proporzionale alla distanza dalla sorgente. Questa regola si traduce facilmente nella nozione che tutti abbiamo imparato a scuola e che dice: “l’intensità della luce emessa da una stella o da una sorgente qualsiasi diminuisce con il quadrato della distanza”. Nella QED la probabilità è proprio il quadrato dell’ampiezza di probabilità e quindi la probabilità diminuisce con il quadrato della distanza. Questa è la vera regola della Natura… Possiamo quindi applicare la nuova regola, sapendo che è verificata in Natura.

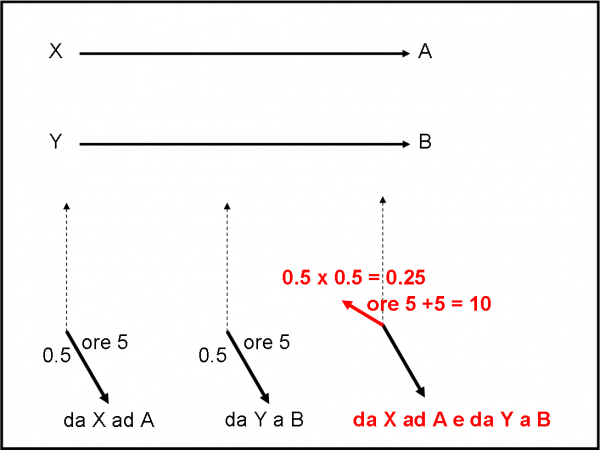
Torniamo allora al nostro evento di Fig. 43 e assumiamo, ad esempio, che la lunghezza della freccia alla distanza A da X si sia ridotta a 0.5. Assumiamo anche che la lancetta si fermi sulle ore 5. La stessa identica cosa succede per il tragitto YB. Anche la freccia relativa alla luce di Y che giunge in B si è ridotta a 0.5 e la lancetta segna le 5. La luce è monocromatica e le distanze XA e YB sono identiche. Posso concludere che la probabilità dell’evento è il 100%? Assolutamente no, dato che, come già ripetuto fin troppe volte, la traiettoria ha una freccia con una certa probabilità, che abbiamo appena calcolato. Bene, per conoscere la probabilità finale dell’evento dobbiamo moltiplicare tra loro le due frecce. Il metodo lo conosciamo bene: si moltiplicano “aritmeticamente” le ampiezze e si sommano le rotazioni della lancetta dei due percorsi. In conclusione, l’ampiezza di  probabilità (la freccia) finale dell’evento è dato da 0.5 x 0.5 = 0.25 e la sua direzione segna le ore 10.

Attenzione: non devo sommare vettorialmente le due frecce, dato che non sono vie alternative (o una o l’altra), ma sono proprio strade indipendenti che portano ognuna al “successo” di una parte dell’evento. In questa ottica, è proprio come se fossero passi successivi di un singolo evento.

Ma siamo sicuri di avere agito bene? Non ci siamo, forse, dimenticati qualcosa? Direi proprio di sì. Quella descritta è solo una delle vie possibili perché si verifichi l’evento. Ne esiste, infatti, un’altra: il fotone di X può raggiungere B e quello di Y può raggiungere A. Nessuno lo vieta, dato che il fotone è descritto da tutte le sue possibili traiettorie. In parole povere, può capitare la situazione di Fig. 44.

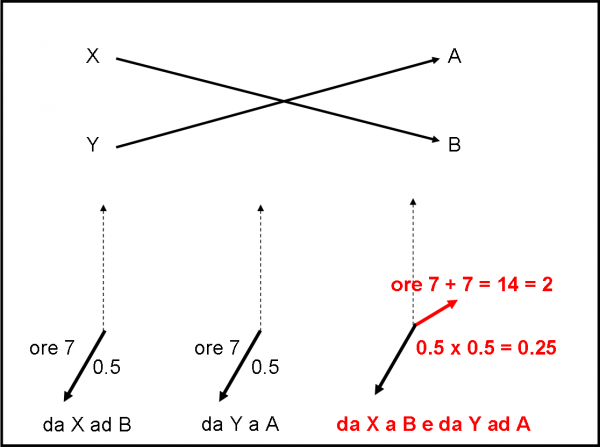
A questo punto dobbiamo fare una riflessione (mentale non sul vetro!). Le distanze XA e XB (così come YA e YB) sono veramente molto simili, quasi perfettamente uguali (la sorgente è molto distante dai rivelatori). Possiamo quindi tranquillamente dire che restano invariate nella via alternativa che dà luogo all’evento. Ciò vuole anche dire che le relative ampiezze di probabilità (le frecce) hanno anche loro un valore di 0.5. Non possiamo, invece, dire lo stesso per la lancetta del cronometro. Anche una piccolissima differenza di distanza fa girare notevolmente la lancetta. Ricordiamoci, infatti, che essa compie 1.440.000 giri per ogni metro. Ne segue che anche una infinitesima variazione di distanza fa variare la direzione della lancetta in modo significativo (un po’ quello che succedeva con lo spessore della lastra di vetro…).

Ne consegue che la seconda via per verificare l’evento comporta una freccia finale di pari ampiezza di quella precedente (0.5 x 0.5 = 0.25), ma con una direzione diversa. A questo punto abbiamo due strade alternative per verificare l’evento. Due strade alternative vogliono dire che dobbiamo combinare le due frecce finali (ottenute con la moltiplicazione) attraverso la somma vettoriale, come illustrato in  Fig. 45.

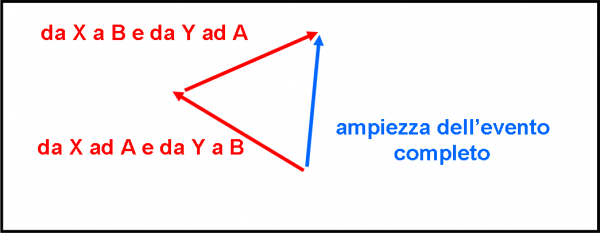
Basta variare di poco la distanza relativa di A e B  o di X e Y (spostando un poco un rivelatore o una sorgente o quello che preferite) e cambiano anche le direzioni delle due frecce ottenute con la moltiplicazione. La somma vettoriale può quindi portare al caso che le due frecce siano perfettamente concordi o perfettamente opposte. Analogamente al caso della doppia riflessione, possiamo, quindi, amplificare al massimo la probabilità finale o annullarla del tutto. Questo fenomeno, che sembra un po’ troppo teorico, a prima vista, ha un suo nome: effetto Hanbury-Brown-Twiss e permette, spostando adeguatamente i rivelatori, di distinguere tra una radio sorgente singola e una doppia, anche quando le due sorgenti sono estremamente vicine tra loro. Non ci vuole molta fatica per dire che siamo di fronte a un fenomeno di interferenza...

Qualcuno potrebbe pensare che abbiamo considerato solo traiettorie rettilinee e quindi due sole alternative.  Ormai sappiamo bene perché si possono considerare solo loro per rappresentare tutte le traiettorie possibili. In ogni modo, non vi è nessun problema. Si potrebbero anche disegnare tutte le traiettorie più strambe che possono verificare l’evento che stiamo analizzando. Il succo non cambierebbe. Possiamo stare tranquilli che le traiettorie strambe darebbero luogo a frecce che girano in tondo e servirebbero ben poco alla probabilità finale!

Ricordiamo, però, sempre, che la freccia finale NON è associata a un fotone, ma all’ampiezza di probabilità della riuscita di un evento. Un fotone parte, fa qualcosa e arriva a destinazione: che probabilità ha di riuscirsi?

Cari amici, alla QED non la si fa… ha una risposta a tutto e sa descrivere come nessuno la Natura. Peccato che non riesca a capirne le regole…

Aspettando la materia

Prima di iniziare il passo successivo verso la materia, mi sembra doveroso parlare del celebre esperimento della doppia fenditura che è uno dei capolavori di Richard. Chi ha letto la descrizione che ne avevo dato a suo tempo (primi capitoli della MQ su astronomia.com) si ricorderà che era  stata un’esposizione abbastanza faticosa, in quanto si era partiti da una visione “normale” delle caratteristiche della luce e, quindi, la contrapposizione particella-onda sembrava veramente un’assurdità senza speranza. Adesso, che abbiamo “capito” come funzionano le regole della QED, vedremo che diventa quasi un gioco da ragazzi, privo di vere difficoltà. Anzi, ci meraviglieremmo se le cose non funzionassero così.

Non solo però, e qui sta la parte più importante dell’esperimento. Saremo anche in grado di “spiegare” tecnicamente perché guardando o -meglio- rilevando il punto di passaggio di un fotone attraverso un foro, il fenomeno d’interferenza scompare. Per fare questo è fondamentale saper definire esattamente un evento e non mischiare tra loro eventi completamente diversi. Le tante parole precedenti sono proprio servite a questo.

Rileggete ancora una volta come si definisce un evento e quali caratteristiche deve avere, tenendo conto che una cosa è sommare vettorialmente due ampiezze (strade alternative per ottenere uno stesso evento), un’altra è moltiplicare le ampiezze (passi intermedi di un evento o passi indipendenti che fanno comunque parte di un solo evento), e un’altra ancora è sommare “normalmente” le probabilità finali (due eventi del tutto separati… ricordatevi la luce che può essere riflessa su R₁ o rifratta su R_2, nella lastra di vetro).

Per non rendere troppo pesante questo articolo, già abbastanza “duro” come concetto, rimando alla prossima lezione la doppia fenditura. In tal modo avremo raggiunto 10 articoli 10 (mamma mia!), dedicati alla luce e alle regole che usa la QED per descriverla.

Poi, faremo veramente entrare in scena gli altri attori. Apriremo la porta che ci introduce all’interazione dei fotoni (e delle loro assurde caratteristiche) con la materia (composta anch’essa da particelle…). Finalmente “capiremo” il perché di certi atti di fede, come l’ampiezza 0.2 della riflessione, il rallentamento subito passando dall’aria al vetro o all’acqua, e via dicendo.  Anzi, capiremo che i fotoni fanno ben poco! Vedremo che non sono loro che si riflettono o attraversano una superficie. No, loro danno solo degli “ordini”. In parole più “tecniche”, i fotoni si spostano solo da un elettrone a un altro. Tocca a questi ultimi catturare e riemettere i fotoni che li colpiscono. Insomma, l’attraversamento e la riflessione sono in realtà operazioni che compiono gli elettroni, i veri “manovali” delle interazioni luce-materia. Vedremo anche che ci verrà utile il concetto di spazio-tempo descritto dal cono di luce (su cui ho sempre battuto “duramente”).

Insomma, ne vedremo proprio delle belle!

P.S. Volevo aggiungere un’annotazione. Vi sarete resi conto che certi concetti base li ho ripetuti quasi in ogni articolo. Forse, qualcuno avrà anche “sbuffato”: “Basta, abbiamo capito!”. Tuttavia, ho pensato che il richiamare quasi costantemente a cosa stiamo realmente applicando la QED fosse troppo importate per non tenerlo sempre a mente, rischiando di perderlo di vista… Ormai mi conoscete e mi dovete accettare con tutte le fissazioni e ripetizioni…