Finalmente ci siamo! Abbiamo un bagaglio sufficiente per affrontare (piano, piano) lo studio completo di una funzione, ossia determinare i punti particolari di essa in modo da schematizzare il suo andamento grafico (e non solo). Tutto ciò che abbiamo imparato finora ci servirà, anche se all’inizio sembrerà che si sarebbe potuto fare meno fatica. Per facilità di descrizione (mia e anche vostra) ricomincio la numerazione delle figure. Si apre un mondo matematico del tutto nuovo e affascinante.

Consideriamo una certa funzione. Sia, come al solito, del tipo: y = f(x) Ammettiamo che essa sia descritta da una curva come quella rappresentata nella Fig. 1

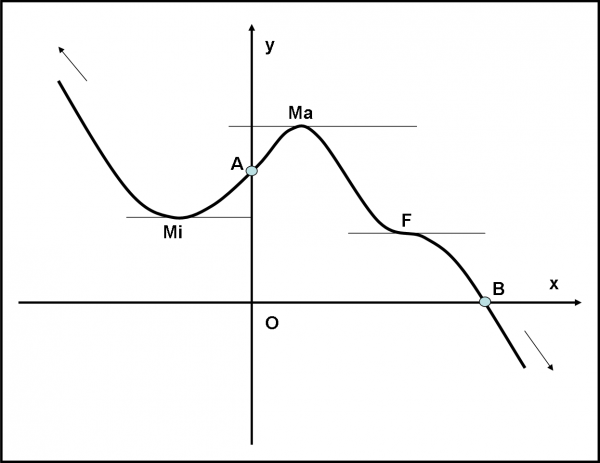
A questo punto ci facciamo una domanda: “Quali sono i punti della curva che la identificano meglio?”. Beh … innanzitutto i punti all’infinito, quelli che ci dicono verso dove sta andando la funzione per valori di x che tendono a meno e più infinito. Ma questo problema l’abbiamo già discusso varie volte. Nel caso in oggetto la y tende a più e meno infinito, rispettivamente.

Escludendo questi “punti” estremi, ne vediamo altri particolari? Sì, sicuramente. Qualcuno è quasi ovvio: le intersezioni con gli assi, B e A. La curva, infatti, taglia sia l’asse delle x che quello delle y. Sarebbe bene determinare questi punti particolari, sempre che esistano, fin dall’inizio. Comincerebbero a darci un’idea di dove si piazzerà la curva. Non trascuriamo il fatto che potrebbero essere anche più numerosi. Vi è qualche difficoltà a determinare immediatamente queste intersezioni? Assolutamente no! Ormai, conosciamo abbastanza bene le funzioni per poter dire che le intersezioni con l’asse delle y si trovano ponendo nella funzione x = 0. Se, infatti, un punto ha l’ascissa uguale a zero vuol dire che la funzione tocca l’asse y proprio in quel punto. Analoga situazione per l’asse x. Per trovare le intersezioni con l’asse x, basta inserire zero al posto della y, ossia scrivere y = f(x) = 0.

Ho detto finora cose semplicissime. Prendiamo, ad esempio, la retta y = ax + b. Qual è l’intersezione della retta con l’asse y? Basta scrivere zero al posto di x, ossia: y = a 0 + b = b Ne segue che il punto intersezione con l’asse y è dato da P(0,b). Qual è, invece, l’intersezione con l’asse x? Basta inserire zero al posto di y. Si ha: 0 = ax + b ax = -b x = -b/a L’intersezione Q con l’asse delle x è, quindi: Q(-b/a,0). Ovviamente, il caso della retta non necessita veramente di trovare le intersezioni con gli assi, dato che per disegnarla basta determinare due suoi punti qualsiasi. Il discorso cambia se avessimo una funzione più complicata. Ci ritorneremo più avanti, ma, intanto, cominciate a notare che per trovare questi “zeri” potrebbe esserci bisogno di risolvere equazioni di secondo grado o anche di grado superiore. Ecco perché le ho richiamate recentemente.

Torniamo alla Fig. 1. Punti particolari ve ne sono ancora e sicuramente molto più interessanti. Ne vediamo tre. I primi due sono facilmente descrivibili. Il primo è un minimo (Mi) e il secondo è un massimo (Ma). Potremmo descriverli in vari modi, come, ad esempio, dire che è un punto in cui la curva smette di scendere e comincia a salire (minimo) o che smette di salire e inizia a scendere (massimo).

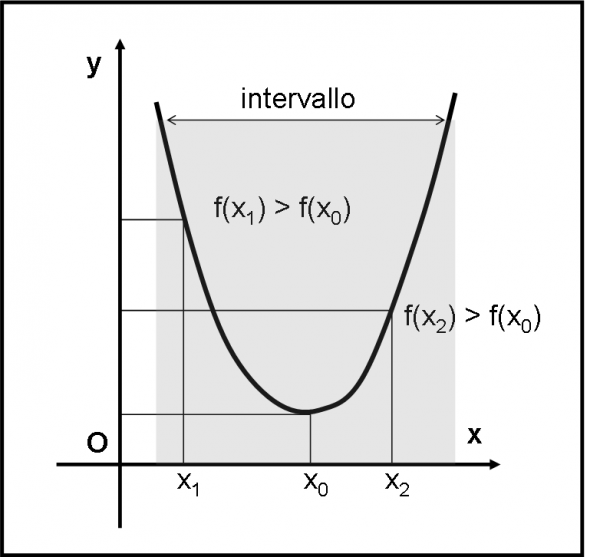
Tuttavia, è meglio utilizzare un linguaggio puramente matematico (se no che matematica staremmo facendo…?). x₀ è l’ascissa di un punto di minimo se, in un intervallo attorno a x₀, vale sempre f(x₀)< f(x). In altre parole, se la y relativa a x₀ è il valore più basso in un certo intervallo di x attorno a x₀. Possiamo fare i raffinati e mostrare la definizione attraverso la Fig. 2. Come avete visto, sono partito, nuovamente, con discorsi di una banalità disarmante. Non facciamoci, però, ingannare dalla matematica. Parte sempre con la massima semplicità e poi si complica via via senza quasi accorgersene. E’ meglio, quindi, non lasciarsi mai andare a troppa “sufficienza”. Anzi, quando sembra eccessivamente elementare è proprio il momento in cui bisogna porre la massima attenzione. Ad esempio, stiamo attenti al concetto di “intervallo”. Non ho detto niente su quanto può essere grande. Infatti, l’importante è che esista un intervallo maggiore di zero, pur piccolo a piacere, in cui vale quanto detto prima.

Il secondo punto particolare è del tutto analogo al minimo, ma inverte completamente la situazione. In esso la funzione smette di crescere per cominciare a decrescere. Potete facilmente ricavare da soli la definizione matematica di massimo: x₀ è l’ascissa di un punto di massimo se, in un intervallo attorno a x₀, vale sempre f(x) < f(x₀).

Attenzione! Quando inseriamo i segni > e <, ricordiamoci che stiamo lavorando con numeri sia positivi che negativi e che qualsiasi numero negativo è sempre minore di un numero positivo. Non solo, ma anche che un numero negativo di valore assoluto piccolo è maggiore di un numero negativo di valore assoluto più grande. So che è una banalità, ma non dimentichiamocelo… In poche parole, -3 > -5, così come 2 > -3. Non facciamo confusione, mi raccomando…

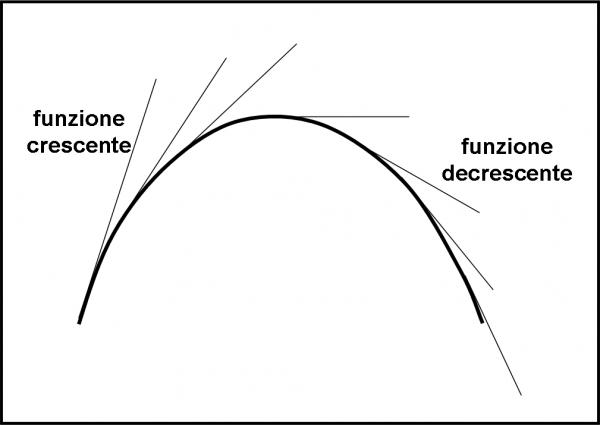
Prima di andare avanti, mi permetto di essere un po’ noioso e darvi anche la definizione di funzione crescente e decrescente. Capisco che è qualcosa di ovvio, ma la matematica impone le sue regole formali. Una funzione è crescente in un certo intervallo se per ogni punto dell’intervallo per cui x₁ < x₂, vale anche f(x₁) < f(x₂). Una funzione è decrescente in un certo intervallo se per ogni punto dell’intervallo per cui x₁ < x₂, vale anche f(x₁) > f(x₂). Se nell’intervallo scelto ci fosse un massimo o un minimo non varrebbero, ovviamente, le definizioni di prima e quindi i massimi e minimi non sono altro che cambiamenti drastici tra situazione di funzione crescente e funzione decrescente (e viceversa).

A questo punto, cominciamo a diventare un po’ più seri. Una funzione crescente ha anche un’altra caratteristica fondamentale: in ogni suo punto la derivata, ossia il coefficiente angolare della tangente, è positivo, ossia la tangente tende verso “l’alto”. In caso di funzione decrescente avviene il contrario.

Non è difficile concludere che nei punti di massimo e di minimo, dovendo passare da fase crescente a fase decrescente (e viceversa), la tangente deve essere parallela all’asse delle x, ossia avere coefficiente angolare uguale a zero, ovvero, la derivata calcolata nei punti di massimo e minimo deve essere uguale a zero.

Ridendo e scherzando abbiamo dedotto un risultato strabiliante per lo studio delle funzioni. Come si può fare per trovare i punti di massimo e minimo di una funzione? Mi vergogno quasi a dirlo: “Basta trovare i valori di x che annullano la derivata della funzione!”. Quanto detto è riassunto nella Fig. 3.

Avete capita l’importanza della derivata? Al di là delle sue infinite applicazioni, permette di trovare velocemente i punti in cui una certa funzione presenta un massimo o un minimo. Basta uguagliare a zero la derivata e risolvere l’equazione in x. Non possiamo certo provarlo per la retta che non ha massimi e minimi. Infatti, la derivata non può mai essere uguale a zero dato che è una costante che è anche il celeberrimo coefficiente angolare. Nessun problema.

Possiamo considerare un’altra curva “facilissima”, la parabola y = x². Calcolare la derivata è ridicolo e vale y’ = 2x. Altrettanto ridicolo è porla uguale a zero, ossia: y’ = 2x = 0 L’unico valore di x che può annullare la derivata è proprio x = 0. Il punto corrispondente ha quindi coordinate P(0,0). Come ho fatto a calcolare la y del punto? Nel modo più ovvio: inserendo zero al posto di x nella funzione di partenza (è o non è un punto della curva?). Nel caso della parabola y = x², si ha y = 0² = 0. Il punto P è, per definizione, un punto di massimo o di minimo.

La derivata prima non può dirci di più, dato che per lei entrambi i punti hanno la stessa caratteristica: annullarla. In prima approssimazione, non è però difficile capire in che caso ci troviamo: basta vedere se l’ordinata di un punto a sinistra e di uno a destra della x che annulla la derivata, sono entrambe maggiori o minori di quella del punto con derivata uguale a zero. Nel primo caso avremmo un minimo, nel secondo un massimo. Nel caso della parabola, siamo, ovviamente, nel primo caso. Scegliendo, ad esempio, x₁ = -1 e x₂ = 1, otteniamo y₁ = (-1)² = 1 e y₂ = 1² = 1. Dato che 1 > 0, il punto P è un minimo, come sappiamo bene, conoscendo perfettamente la curva della parabola.

Tuttavia,vi è un sistema molto più “aristocratico” per capire se un punto è un massimo o un minimo: calcolare la derivata seconda. Piano, piano… ci torneremo sopra a tempo debito.

No, non mi sono dimenticato del terzo punto particolare, F, della Fig. 1. Come possiamo descriverlo? La funzione continua a essere decrescente sia prima che dopo il punto, tuttavia la sua tangente è nuovamente orizzontale nel punto F, ossia la derivata vale nuovamente zero. Esistono quindi punti che, pur avendo una tangente orizzontale, non cambiano la propria tendenza a decrescere (o, ovviamente, anche a crescere). Per poterli definire meglio, dobbiamo introdurre la concavità della curva prima e dopo il punto. Essa si inverte: se prima era verso l’alto, dopo va verso il basso. Potrei fare anche il super-raffinato e dirvi che una concavità verso l'alto (o il basso) vuole dire che il centro del cerchio osculatore sta nella parte alta (o bassa). Mi spiego meglio con la Fig.4.

A sinistra abbiamo una curva con una concavità diretta verso l’alto (possiamo anche chiamarla concava), a destra con una concavità diretta verso il basso (convessa). Il punto di flesso è un punto dove le concavità si invertono. In altre parole, prima del flesso la tangente alla curva tende a diminuire sempre più il proprio coefficiente angolare (in valore assoluto) fino a raggiungere zero, proprio come succederebbe in un minimo, ma poi ricomincia ad aumentarlo e si comporta come se avesse superato un massimo. E’ come se unissimo minimo e massimo e usassimo solo il primo ramo del minimo e il secondo ramo del massimo.

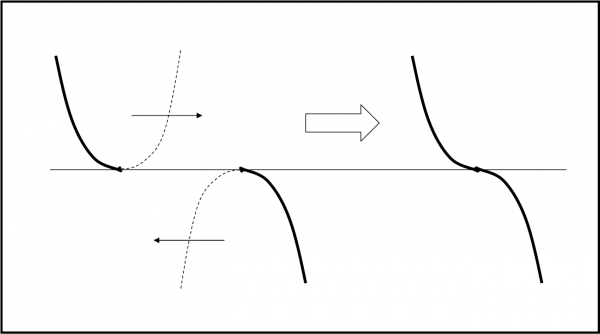
Il problema è che, cercando gli zeri della derivata, potremmo trovare anche questo tipo di situazione e non dobbiamo confonderla con un semplice massimo o un semplice minimo. Il punto così “antipatico” si chiama flesso orizzontale e può essere studiato “localmente”, come già fatto per i massimi e i minimi. Basta prendere un intervallo attorno a lui e vedere se la funzione è sempre crescente o decrescente, sia prima che dopo.  Nel primo caso è un flesso ascendente, nel secondo caso è un flesso discendente. Le cose diventano matematicamente più eleganti passando, nuovamente, alla derivata seconda.

Voglio preannunciarvi che esistono altri tipi di flesso, ossia quelli obliqui. In realtà nella curva di Fig. 1 ne esiste SICURAMENTE uno (provate a trovarlo empiricamente…). Essi sono punti in cui tutto segue le regole dette finora, con la sola differenza che nel punto di flesso la tangente non è orizzontale, ma è una retta obliqua. In generale, possiamo dire che il flesso di una curva è un punto in cui la curva attraversa la tangente in quel punto. Prima, è sempre sopra (o sotto) e dopo è sempre sotto (o sopra). Ciò è ovviamente valido anche nel caso del flesso orizzontale, ossia con tangente parallela all’asse delle x. Esistono, ovviamente, anche flessi che hanno la tangente verticale, ma per adesso non occupiamocene… così come rimandiamo a dopo anche lo studio dei flessi obliqui in generale. Finora abbiamo solo introdotto alcuni punti particolari (i più comuni). La prossima volta vedremo di stabilire la loro esistenza e rappresentarli nel grafico, in modo da avere una visione pressoché completa dell’andamento di una funzione.  Come già accennato, faremo uso della derivata seconda  (e anche di più). Ma per adesso basta e avanza.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica