Iniziamo il nostro viaggio verso i diagrammi di Feynman: forza, coraggio e molta attenzione.

Tre lettere per scrivere la Natura

La prima cosa da chiedersi è: “Dopo aver convissuto a lungo con le ampiezze di probabilità e avere imparato a sommarle, a moltiplicarle e a spezzarle in parti sempre più piccole, possiamo definire in qualche modo i sub-eventi “elementari”? In altre parole, è possibile selezionare pochi “pezzi” fondamentali, come fossero lettere di un alfabeto, che ci permettano di descrivere attraverso parole e frasi ogni fenomeno della Natura? E se fosse vero, quante sarebbero queste lettere?”. Beh… siamo veramente fortunati. La risposta è positiva e il numero è ridicolo: solo tre azioni sono sufficienti a descrivere ogni possibile fenomeno associato alla luce e agli elettroni, ossia alla luce e alla materia.

Prima di enunciarle, ricordiamo, ancora una volta, che sia per i fotoni che per gli elettroni vale una regola generale: se entrambi vengono considerati su scale molto grandi, si dimostrano a tutti gli effetti come particelle, ma il loro comportamento cambia drasticamente se li si analizzano su scale molto piccole. Pensate ad esempio agli elettroni. All’interno di un atomo, essi perdono del tutto le loro caratteristiche di corpuscoli, dato che non vi è posto per traiettorie  e orbite ben definite. Essi, come i fotoni, possono solo essere descritti come ampiezze di probabilità di occupare una certa posizione. Anche per loro si devono sommare frecce e le interferenze diventano di primaria importanza.

Vedremo che non solo gli elettroni si comportano così, ma tutte le particelle elementari, come gluoni, quark, neutrini e compagnia bella.  Un discorso ben più generale di quanto non ci racconti l’interazione tra luce ed elettroni. Tuttavia, proprio per le caratteristiche simili, possiamo benissimo limitarci, per adesso, a fotoni ed elettroni.

Definiamo, finalmente, le tre azioni (tre e solo tre) che stabiliscono l’alfabeto per tutte le frasi della QED, ossia per tutti i fenomeni che ci mostra la Natura.

(1) Un fotone viaggia da un punto a un altro.

(2) Un elettrone viaggia da un punto a un  altro.

(3) Un elettrone è capace di assorbire o di emettere un fotone.

Siete delusi? Probabilmente sì, dato che a parte la (3) sembra di avere detto cose di un’ovvietà mostruosa. La (3) appare un po’ più impegnativa e va sicuramente studiata in dettaglio. Tuttavia, anche le altre due sono decisive e importanti, dato che devono essere descritte nel nuovo campo di gioco di Alice, ossia lo spazio-tempo.

Ricordiamo, inoltre, che ognuna di queste azioni ha una sua ampiezza di probabilità (una freccia) che può essere calcolata secondo regole ben definite. Queste regole sono ferree e non bisogna dimenticarle, anche se una loro rappresentazione completa abbisogna di una matematica superiore. Nessun problema, dato che noi le tratteremo solo graficamente. Per fare ciò, però, è necessario preparare il foglio del disegno e questo è un qualcosa che ha bisogno di essere compreso perfettamente nella sua essenza, senza fare confusione con lo “spazio” in cui viviamo.

Non è la prima volta che disegniamo lo spazio-tempo, ma ogni volta si rischia di fare un po’ di confusione. Ricominciamo, quindi, da zero e consideriamoci dei bambini che si avvicinano a un quaderno per la prima volta e cercano di scrivere sulla sua prima pagina le uniche tre lettere dell’alfabeto.

Un quaderno molto speciale

La pagina del quaderno non ha righe o quadretti. E’ completamente bianco. Sta a noi preparala per ciò che vogliamo rappresentarci sopra. Permettetemi qualche esempio: se volessimo disegnare il profilo dell’Italia, dovrei mettere come coordinate delle distanze o -se preferite-  la latitudine e la longitudine. Se, invece, volessimo vedere com’è variata la popolazione della Terra, dovremmo inserire il numero di abitanti e gli anni. Se, ancora, volessimo sapere la struttura della nostra atmosfera, metteremmo come coordinate, ad esempio, la temperatura e l’altezza dal suolo. E mille altri esempi simili. Ogni disegno, magari proprio lo stesso (una retta, un quadrato, un cerchio o quello che volete), acquista un significato diverso se si cambiano gli assi di riferimento.

Nella pagina di Alice, pronta per ricevere le tre lettere della QED, si devono inserire lo spazio e il tempo. Un bel pasticcio, dato che lo spazio è definito da tre dimensioni. Se gli aggiungiamo il tempo, avremmo bisogno di quattro dimensioni. Come potremmo mai trasformare un foglio in un campo di gioco a quattro dimensioni? Impossibile anche per la QED e le sue lettere.

Poco male, dato che conosciamo già la semplificazione che si può fare senza ledere i concetti base: basta considerare lo spazio come una retta, ossia assumere che ogni punto dello spazio e ogni traiettoria percorribile sia contenuta nell’asse delle x. Lo abbiamo fatto spesso e, in fondo, non ci ha mai spaventato più di tanto. Possiamo accettare questa semplificazione, mettendoci, però, bene in testa che qualsiasi movimento spaziale di una particella può avvenire solo lungo la linea orizzontale. I fenomeni di riflessione, rifrazione e cose del genere, che abbiamo trattato precedentemente, avvengono, perciò lungo questa retta.

No, non sto dicendo cose assurde o banali. Tra poco, vedremo che le particelle sembreranno riflettersi o rifrangersi, ma non commettiamo l’errore di pensare  a qualcosa che si muova diagonalmente nello spazio, come succedeva alla luce che si dirigeva verso uno specchio o usciva da una fenditura. Mi raccomando!

A questo punto, l’asse y è libero e può essere regalato al tempo. Il nostro foglio è diventato lo spazio-tempo. Per prendere dimestichezza con questo campo da gioco, impariamo, innanzitutto, a disegnarci sopra qualcosa che si riferisca alle azioni di tutti i giorni. Visto che l’abbiamo considerato un campo sportivo, consideriamo come “oggetto” da rappresentare una pallina da tennis, come vediamo nella Fig. 47.

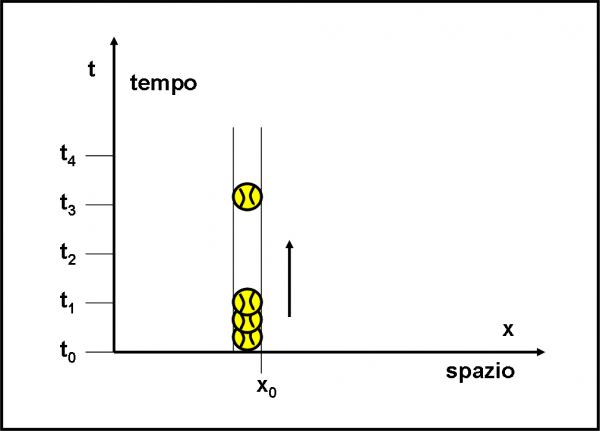
Immaginiamo che la pallina sia ferma, in un certo punto del “normale” campo da tennis (che è tutto contenuto nell’asse x). Il tempo, invece, continua a scorrere andando verso l’alto (attenzione: la freccia del tempo ha questo verso e sarà sempre lo stesso). Come possiamo disegnare la nostra pallina in questo campo da gioco veramente speciale? Non certo come un punto, dato che la sua coordinata “tempo” continua a cambiare. Non cambia invece la x₀, ossia la sua posizione nello spazio. Il movimento spazio-temporale della pallina è quindi una linea verticale. In questo campo da gioco, la pallina ha una ben definita traiettoria, alla quale possiamo associare un’ampiezza di probabilità di accadere.

Aggiungiamo, adesso, alla figura precedente una parete  che al tempo t₀ si trova in x₃ (Fig. 48).

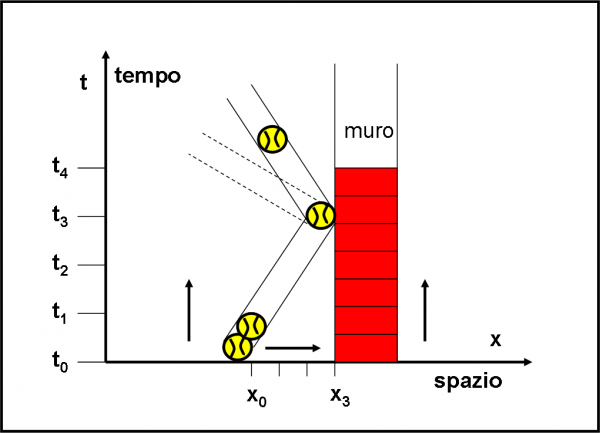
Essa non può certo cambiare posizione spaziale e quindi al passare del tempo mantiene sempre la stessa posizione e descrive la traiettoria parallela all’asse del tempo (come faceva la pallina nel caso precedente). Adesso, però, la pallina si muove in modo uniforme nello spazio andando verso la parete. Al tempo t₀ si trova in x₀, al tempo t₁ in x₁ e via dicendo, fino a toccare la parete al tempo x₃. Non riuscendo, ovviamente, a penetrare dentro la parete, la pallina è costretta a rimbalzare e al tempo t₄ si trova nuovamente nella posizione x₂ e in t₅ in x1. Non è detto, però, che la pallina torni indietro nello spazio così come si è mossa all’andata. Potrebbe, ad esempio tornare in x₀ al tempo t₄ (ossia, muoversi più velocemente che all’andata, avendo percorso uno spazio maggiore in un tempo uguale), oppure in x₁ al tempo t₄ (si muoverebbe più lentamente). La pallina, in ogni caso, descrive una traiettoria spazio temporale che a un certo momento (impatto con la parete) cambia percorso, tornando da dove era venuta. La pallina si è sicuramente mossa anche nello spazio, ma ha percorso il tratto da x₀ a x₃ e poi è tornata indietro lungo la stessa direzione. In qualche modo, dal punto di vista spaziale, la pallina ha invertito di 180° la sua direzione di marcia.

Nel foglio spazio temporale ha invece descritto una linea spezzata. Essa rappresenta una traiettoria spazio temporale che possiede una certa ampiezza di probabilità di essere realmente percorsa. Attenzione: so di essere noioso, ma vi prego di non confondere la figura precedente con la visione puramente spaziale, in due dimensioni, dell’urto di una pallina tirata contro un muro diagonalmente. Se pensiamo a questo, fermiamoci, scrolliamo la testa e rimettiamo sullo zero il nostro cervello!

Beh… penso proprio che non abbiate difficoltà a ricordare cosa significhi la traiettoria nel piano spazio-tempo: il suo coefficiente angolare è la velocità della pallina, ossia lo spazio percorso in un certo intervallo di tempo. Più la retta è inclinata rispetto all’asse delle x e minore è la velocità relativa.

Dato che a noi non interessano le palline da tennis (troppo grandi, così come le dimensioni di un vero campo da tennis), ma le particelle come i fotoni e gli elettroni, cerchiamo di trasformare la scala degli assi cartesiani x e t.

Il fotone, su spazi abbastanza lunghi e nel vuoto, viaggia lungo una linea retta (lo abbiamo dimostrato). La sua velocità può essere considerata costante e si indica con c, che vale circa 300 000 km/sec. Mettere i metri in ascissa e i secondi in ordinata sarebbe una pessima scelta della scala, dato che tutte le particelle viaggiano molto velocemente. Scegliamo, allora, la scala in modo che la traiettoria di un fotone che viaggia a velocità c sia descritta da una retta a 45°. Ciò vuol dire che un intervallo pari a n centimetri o millimetri o metri o quello che preferite deve essere “lungo” come l’intervallo di tempo che la luce impiega a percorrere n. Se n fosse di 30 centimetri, lo stesso segmento sull’asse y sarebbe pari a un miliardesimo di secondo, così come un intervallo di 300 000 km corrisponderebbe esattamente a un secondo.

Con questo cambiamento di scala, la velocità di un fotone che descriva la traiettoria spazio-temporale da x₁,t₁ a x₂,t₂ (o da x2,t1 a x1,t2) è proprio c (Fig.49).

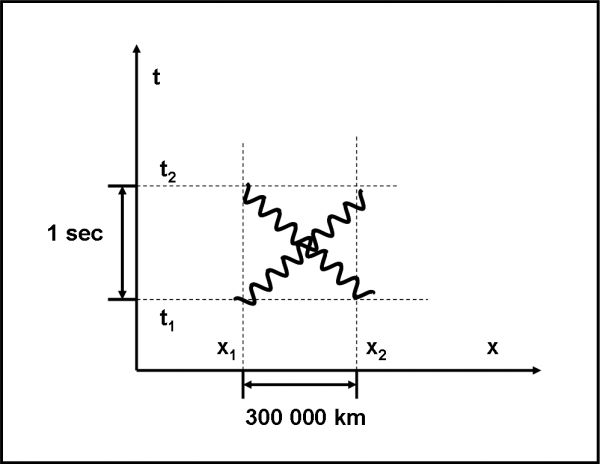
La cosa veramente importante è però, un’altra: se la traiettoria è più ripida della retta a 45° la velocità è minore di c (minore spazio nell’unità di tempo), mentre se la retta è meno inclinata di 45°, la velocità è maggiore di c (maggiore spazio nell’unità di tempo). Notate che abbiamo scelto (anzi, l’ha deciso Feynman) una rappresentazione simbolica per il fotone: lo abbiamo descritto come una linea ondulata. Niente a che vedere con un’onda, dato che tutte le particelle si comportano nello stesso modo. E’ solo una scelta per riconoscere i fotoni dai suoi amici di avventura.

Fermiamoci un attimo per vedere come ciò che abbiamo introdotto si potrebbe applicare alla vita di tutti i giorni. Infatti, anche noi possiamo tracciare le traiettorie di un certo oggetto nello spazio-tempo. Tuttavia, abbiamo dei blocchi fisici insormontabili. Consideriamo la Fig. 50, dove l’oggetto P può muoversi verso il futuro alla sua massima velocità, ossia c (ce l’ho dice il Sig. Einstein e lui di macrocosmo se ne intende e molto!).

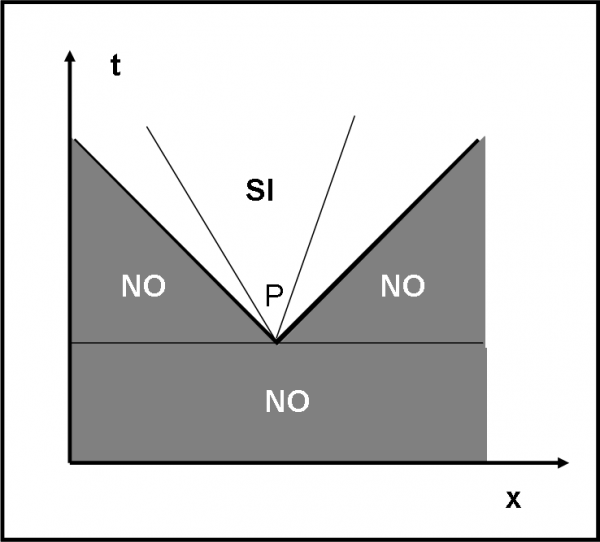
Otteniamo una coppia di rette che formano un angolo di 90° tra di loro. Esse possono, infatti, essere inclinate di 45° rispetto all’asse dello spazio, non uno di meno, altrimenti accetteremmo velocità maggiori di quelle della luce. Qualsiasi traiettoria contenuta all’interno delle due rette è possibile, mentre quelle esterne sono IMPOSSIBILI per definizione. Vi è però un altro vincolo. L’oggetto non può descrivere traiettorie che vadano in verso opposto, dato che vorrebbe dire viaggiare verso il passato. Anche questo caso è vietato dalla fisica. Le uniche traiettorie possibili sono quindi quelle contenute nella parte bianca del diagramma. Esso è un triangolo che altri non è che la sezione, nel piano della figura, del cono di luce futuro di un oggetto P.  Il nostro modo di vivere ha a disposizione solo una piccola parte del foglio! Nel mondo di Alice, invece, qualsiasi traiettoria è possibile.

Torniamo al nostro fotone. Lui è libero di muoversi dove vuole. Ricordo ancora che il foglio rappresenta una parte di spazio-tempo piccolissimo, dove è possibile qualsiasi cosa, come, ad esempio (e lo abbiamo già visto) andare lungo traiettorie che non sono rettilinee (esperimento della doppia fenditura) e che possono causare fenomeni “assurdi” come l’interferenza. E’ il momento di introdurre la prima lettera del nostro alfabeto.

Abbecedario

Essa dice: un fotone viaggia da un punto a un altro. In parole più tecniche questa lettera significa: un fotone che occupa una posizione (x₁,t₁) ha una certa ampiezza di probabilità di apparire in (x₂,t₂). Questa ampiezza di probabilità viene indicata con P(A -->B) o più facilmente P(A,B). Il calcolo di P(A,B) non è cosa banale, ma la matematica è capace di farlo con grande accuratezza. L’ampiezza dipende essenzialmente dalla differenza x₂-x₁ e dalla differenza t₂–t₁. Più esattamente dalla differenza dei loro quadrati, ossia (x₂-x₁)² – (t₂-t₁)². Risulta immediato accorgersi che la traiettoria rettilinea tra A e B è proprio quella per cui questa differenza diventa zero, ossia quando x₂-x₁ = t₂-t₁, cioè quando la traiettoria rappresenta la velocità della luce convenzionale, uguale a c.

Possiamo facilmente concludere che l’ampiezza totale P(A,B) è la somma di tante ampiezze e che quelle intorno alla velocità della luce c danno il maggior contributo all’ampiezza di probabilità finale. Lo stesso identico discorso che avevamo fatto quando avevamo dimostrato perché la luce, su grandi distanze, si muove di moto rettilineo. Abbiamo cambiato campo di gioco, ma le regole sono sempre le stesse, quella della QED.

Ricapitoliamo un attimo: nei capitoli precedenti avevamo visto che la luce può anche non andare lungo traiettorie rettilinee. Adesso, nel mondo di Alice e sul suo quaderno, abbiamo visto che la luce può anche viaggiare a velocità diverse da c. Un bell’inizio, non c’è che dire! Il contributo di traiettorie diverse da quelle del senso comune possono non essere trascurabili quando gli spazi da percorrere sono estremamente piccoli. L’interferenza ce lo ha dimostrato e possiamo aspettarcelo anche adesso.

Nel piano spazio-temporale l’azione di andare da A a B viene indicata, come già detto, da una linea ondulata che congiunge A con B. A questa linea è associata la corrispondente P(A,B). P(A,B) è data da una formula che ci è preclusa, ma sappiamo molto bene come si trattano le ampiezze di probabilità! Forse non ce ne siamo accorti, ma la prima lettera del nuovo alfabeto (un fotone va da un punto a un altro) è in grado di descrivere tutta l’ottica e i fenomeni ad essa collegati. Essa rappresenta l’intera teoria della luce.

Nota Bene: in realtà, quanto detto non è proprio vero, dato che, finora, abbiamo trascurato la polarizzazione della luce. Se avremo voglia potremo anche introdurla, ma le cose si complicherebbero un bel po’, non cambiando, però, il succo dell’intera faccenda.

Passiamo alla seconda lettera dell’alfabeto, ossia alla seconda azione fondamentale: un elettrone va da un punto a un altro (ovviamente, sempre nello spazio-tempo). Sembra un’ovvietà, un’estrapolazione immediata della prima lettera. In realtà, la formulazione dell’ampiezza di probabilità associata all’elettrone è più complicata di quella del fotone. Anch’essa dipende dalle differenze tra spazio e tempo, come quella del fotone. Tuttavia, vi sono vari termini aggiuntivi che vengono moltiplicati per un certo numero m. In parole poverissime, l’ampiezza di probabilità E(A,B) dell’elettrone è una combinazione praticamente infinita di P, ognuna moltiplicata per m². Ciò deriva dal fatto che un elettrone per andare da A a B può eseguire diversi cambiamenti di rotta. Può andare, ad esempio, fino a C e poi piegare per finire in B. Un cambiamento di direzione comporta l’aggiunta, al termine “base” P(A,B), di un termine dato da P(A,C) x m² x P(C,B). L’elettrone potrebbe, però, fare due cambiamenti di direzione: andare da A a D, poi da D a E, e, infine, da E a B. L’ulteriore termine da aggiungere sarebbe P(A,C) x m² x P(C,D) x m² x P(D,B). e via dicendo fino all’infinito o quasi. In poche parole m² non è altro che l’ampiezza relativa a un cambiamento di direzione. Ovviamente, più passaggi intermedi si considerano  e maggiore è il contributo di questi all’ampiezza di probabilità E(A,B).

Non vi sarà scappato il fatto che abbiamo eseguito una moltiplicazione di ampiezze, dato che l’ampiezza finale è stata scomposta nei suoi vari passi. Non andiamo oltre perché entreremmo nella matematica più complessa a noi preclusa. Tuttavia, possiamo concludere che l’ampiezza di probabilità del percorso dell’elettrone per andare da A a B è data da E(A,B) e che essa coincide con quella del fotone, quando il numero m diventa zero (tutti i termini aggiuntivi si eliminano).

Torneremo su m, ma, per adesso, accettiamo che l’ampiezza di probabilità di andare da A a B, da parte dell’elettrone, è data da E(A,B), che è quantità piuttosto complicata, ma strettamente collegata a P(A,B). L’azione dell’elettrone viene indicata nel diagramma da una linea continua che congiunge A con B, ma sappiamo benissimo che essa rappresenta un’infinità di linee spezzate, ciascuna con la sua ampiezza, che contribuiscono al valore finale di E(A,B).

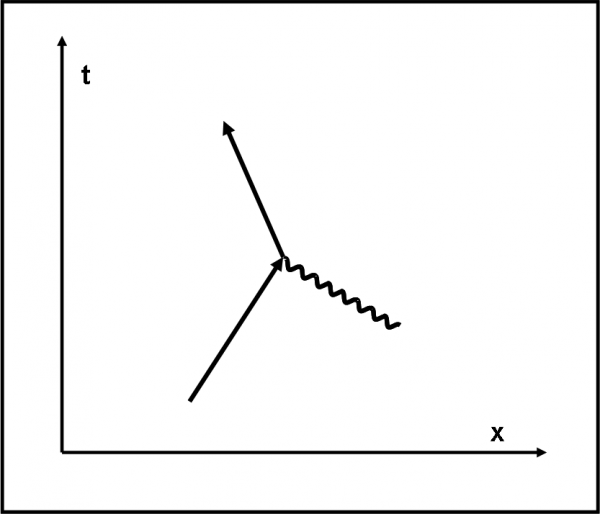
Non ci rimane, adesso, che introdurre la terza lettera, quella apparentemente meno immediata: un elettrone è capace di assorbire o di emettere un fotone. Innanzitutto, facciamo una chiara affermazione: non vi è nessuna differenza sostanziale tra le due azioni sopra descritte. Assorbire o emettere un fotone non cambia assolutamente il processo. Questa azione viene chiamata “accoppiamento” (coupling in inglese). La traiettoria dell’elettrone viene simbolicamente cambiata al momento di un accoppiamento. L’ampiezza di probabilità dell’accoppiamento non ha una formula particolarmente difficile. Essa si riduce a un numero j, che comporta una riduzione di circa 0.1 e una rotazione di 180°. Come possiamo rappresentare nel nostro foglio questa terza azione? Facilissimo: due linee continue (l’elettrone) (munite di una freccia che indica il verso di percorrenza, cosa inutile per il fotone dato che per lui essere emesso assorbito è la stessa cosa) e una un linea ondulata (il fotone), come rappresentato in Fig. 51. Ogni linea ha una sua ampiezza di probabilità, così come l’accoppiamento.Tuttavia, assumendo che il fotone si muova nel verso crescente del tempo (per adesso è meglio rimanere con i piedi per terra), possiamo dire che nella figura il fotone è assorbito. Ci torneremo, comunque, sopra.

Non è assolutamente difficile lavorare su di esse per descrivere situazioni più elaborate.

Iniziamo, dunque, questa impresa. Abbiamo imparato le lettere dell’alfabeto, le abbiamo definite esaurientemente e sappiamo come disegnarle. Proviamo adesso a costruire con esse la prima parola!

Lo facciamo, però, la prossima volta…