Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento

 

Vale la pena riportare per intero un brano tratto dal celebre “Dialogo sopra i Massimi Sistemi del Mondo” di Galileo (chi parla è ovviamente Salviati…):

“Riserratevi con qualche amico nella maggiore stanza che sia sotto coverta di alcun gran navilio, e quivi fate d'aver mosche, farfalle e simili animaletti volanti; siavi anco un gran vaso d'acqua, e dentrovi de' pescetti; sospendasi anco in alto qualche secchiello, che a goccia a goccia vadia versando dell'acqua in un altro vaso di angusta bocca, che sia posto a basso: e stando ferma la nave, osservate diligentemente come quelli animaletti volanti con pari velocità vanno verso tutte le parti della stanza; i pesci si vedranno andar notando indifferentemente per tutti i versi; le stille cadenti entreranno tutte nel vaso sottoposto; e voi, gettando all'amico alcuna cosa, non piú gagliardamente la dovrete gettare verso quella parte che verso questa, quando le lontananze sieno eguali; e saltando voi, come si dice, a piè giunti, eguali spazii passerete verso tutte le parti. Osservate che avrete diligentemente tutte queste cose, benché niun dubbio ci sia che mentre il vassello sta fermo non debbano succeder cosí, fate muover la nave con quanta si voglia velocità; ché (pur che il moto sia uniforme e non fluttuante in qua e in là) voi non riconoscerete una minima mutazione in tutti li nominati effetti, né da alcuno di quelli potrete comprender se la nave cammina o pure sta ferma: voi saltando passerete nel tavolato i medesimi spazii che prima né, perché la nave si muova velocissimamente, farete maggior salti verso la poppa che verso la prua, benché, nel tempo che voi state in aria, il tavolato sottopostovi scorra verso la parte contraria al vostro salto; e gettando alcuna cosa al compagno, non con piú forza bisognerà tirarla, per arrivarlo, se egli sarà verso la prua e voi verso poppa, che se voi fuste situati per l'opposito; le gocciole cadranno come prima nel vaso inferiore, senza caderne pur una verso poppa, benché, mentre la gocciola è per aria, la nave scorra molti palmi; i pesci nella lor acqua non con piú fatica noteranno verso la precedente che verso la sussequente parte del vaso, ma con pari agevolezza verranno al cibo posto su qualsivoglia luogo dell'orlo del vaso; e finalmente le farfalle e le mosche continueranno i lor voli indifferentemente verso tutte le parti, né mai accaderà che si riduchino verso la parete che riguarda la poppa, quasi che fussero stracche in tener dietro al veloce corso della nave, dalla quale per lungo tempo, trattenendosi per aria, saranno state separate...”

Beh… ha detto esattamente le cose che ho cercato di descrivere nel capitolo 0. Meglio ancora, io ho detto esattamente le cose che ha detto Salviati! Riassumendo, ancora una volta: non è possibile, solo con esperimenti di meccanica, rivelare se un sistema è fisso o si muove di moto rettilineo uniforme. Chi viaggia sulla carrozza non può assolutamente capire se si sta muovendo oppure sta fermo, dato che le leggi della fisica rimangono inalterate.

Da un sistema a un altro

Quello che vogliamo fare, adesso, è ricavare le formule che legano le coordinate spazio-temporali di uno stesso evento visto da due diversi sistemi di riferimento e dimostrare proprio che le leggi della fisica non cambiano passando da un sistema all’altro. Mediante questo procedimento troveremo cose molto interessanti come la trasformazione galileiana e l’addizione delle velocità.

Consideriamo due sistemi cartesiani: O(x,y,z,t) e O’(x’,y’,z’,t’). Entrambi si muovono di moto rettilineo uniforme rispetto a un ipotetico riferimento fisso. Possiamo fare due semplici semplificazioni che derivano dal principio d’inerzia, ossia da quanto abbiamo detto precedentemente. Innanzitutto, considerare fisso uno dei due sistemi e riferire il moto del secondo al primo. In altre parole, considerare fisso O e studiare il movimento di O’ rispetto a lui. Il movimento, inoltre, può avvenire in qualsiasi direzione, ma è possibile scegliere gli assi cartesiani in modo che il movimento avvenga solo lungo l’asse x, coincidente con x’.

Dobbiamo fare, inoltre, un’altra ipotesi di partenza: il tempo t è identico al tempo t’, ossia scorre nello stesso modo in entrambi i sistemi di riferimento. In altre parole, gli orologi in O e O’ segnano sempre la stessa ora. Questa assunzione sembrerebbe derivare da una mancanza di approfondimento da parte di Galileo. Invece, il grande pisano era del tutto conscio del fatto che per essere sicuri che gli esperimenti fatti nei due sistemi di riferimento fossero veramente istantanei si poneva il problema della velocità della luce. Infatti, per dare il via allo sperimentatore che si sarebbe mosso, Galileo doveva fare segnali con una lanterna. Egli fece molti tentativi a distanze crescenti e ne dedusse, ovviamente, che la luce era sicuramente “rapidissima”, concludendo che, qualsiasi possibile valore essa avesse realmente avuto, sarebbe stata del tutto irrilevante ai fini pratici. L’uguaglianza t = t’ non è quindi assolutamente arbitraria, ma basata anch’essa sulla sperimentazione, in accordo col metodo scientifico.

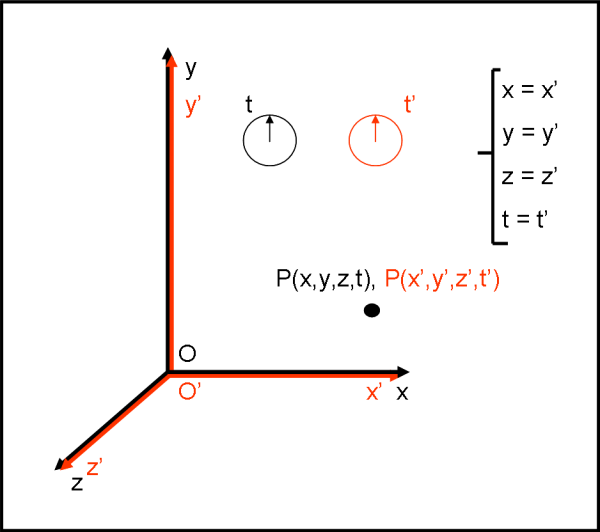
Assumiamo che all’istante t = 0, O’ coincida con O, come rappresentato in Fig. 1. Entrambi gli orologi segnano t =t' = 0 e le coordinate nei due sistemi sono perfettamente identiche.

Facciamo adesso muovere O’ con velocità v₀ costante rispetto ad O, come mostra la Fig. 2.

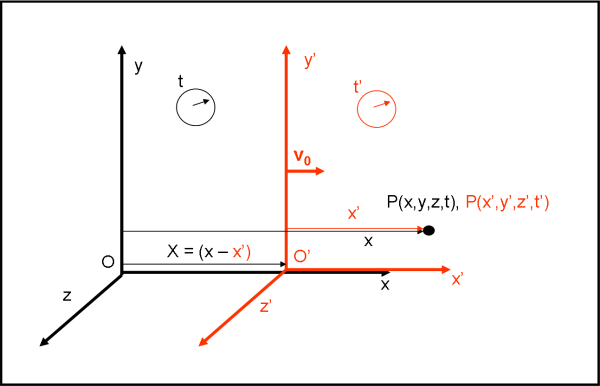
Dopo un  tempo t = t’ (gli orologi segnano lo stesso tempo), l’ascissa del punto O’ rispetto a O sia X. Per definizione di velocità:

v₀ = (X -0)/(t -0) = X/t

ossia:

X = v₀ t

Un punto P qualsiasi ha coordinate (x,y,z,t) nel sistema O e coordinate (x’,y’,z’,t’) nel sistema O’. Per come è stato costruito il secondo sistema, valgono sicuramente le uguaglianze:

y = y’

z= z’

t = t’

Calcoliamo, invece, la relazione tra x’ e x

Dalla figura si ha subito:

x = x’ +OO’ = x’ + X = x’ + v₀ t

Otteniamo, allora:

x = x’ + v₀t

y = y’

z = z’

t = t’                        …. (1)

Queste relazioni descrivono le trasformazioni galileiane per passare da un sistema di riferimento inerziale a un altro (ottenuto per pura traslazione, ossia attraverso una velocità relativa costante).

Per semplificare i passaggi successivi, trascuriamo l’asse z (lo potremmo immaginare perfettamente diretto verso di noi). D’altra parte sappiamo che nulla cambia, dato che z’ = z.

Le velocità si sommano

Immaginiamo, adesso, che il nostro punto P si muova con una certa velocità v’ nel sistema di riferimento di O’. Attenzione: questa velocità può anche non essere COSTANTE. Essa si riferisce a un certo fenomeno fisico che capita nel sistema di O’, ma non inficia assolutamente la definizione di sistema inerziale per O’. Perché un sistema non sia più inerziale è necessario che la velocità tra i due sistemi sia variabile, ma non certo che il fenomeno descritto dal punto P sia legato a una velocità costante. Siamo nel caso dell’articolo 0. La pallina cade sotto l’azione di una velocità variabile, legata all’accelerazione di gravità, ma il sistema carrozza rimane inerziale, dato che si muove rispetto a Salviati con velocità rettilinea uniforme.

A questo punto conosciamo la velocità costante v₀ e quella qualsiasi v’. Per semplicità, imponiamo che anche la velocità v’ vada nella stessa direzione di v₀. Come facciamo a determinare la velocità v del punto P rispetto al sistema di riferimento O? Beh… ormai siamo capaci di effettuare le derivate e non ci dobbiamo più spaventare ad applicarle. Sappiamo benissimo che la velocità può essere scritta come ds/dt, ossia come derivata dello spazio rispetto al tempo.

Prendiamo, allora, la prima relazione delle trasformazioni di Galileo (che descrive la relazione tra le ascisse di un punto P qualsiasi):

x = x’ + v₀ t

Per calcolare la velocità del punto P, basta derivare questa espressione rispetto al tempo (la derivata determina, infatti, la variazione istantanea dell’ascissa rispetto al tempo, ossia proprio la velocità):

dx/dt = dx’/dt + d(v₀ t)/dt

il primo termine è proprio la velocità v cercata (la variazione di x nel sistema O). Il secondo termine è la velocità v’ (la variazione di x’ nel sistema O’). Per il terzo termine dobbiamo ricordare la derivata di un prodotto, o -ancora meglio- la derivata del prodotto di una variabile  per una costante. In un modo o nell’altro, si ricava che la derivata di un prodotto di una costante per una variabile è uguale al  prodotto della costante per la derivata della variabile. In altre parole, la costante esce dall’operazione derivata senza nessun problema (non confondetevi, però: la derivata di una costante è sempre zero). Un’ottima occasione per ripassare la derivata: avete voluto le derivate? Adesso usiamole nella pratica!

In poche parole:

d(v₀ t)/dt = v₀ dt/dt = v₀       (dt/dt è ovviamente uguale a 1).

Alla fine si ottiene la fondamentale relazione:

v = v’ + v0   …. (2)

Perché è così fondamentale, pur essendo di una semplicità spaventosa oltre che estremamente intuitiva? Perché sarà proprio questa espressione che diventerà insostenibile quando le velocità si avvicineranno a quella della luce. Capire la rivoluzione di Einstein senza aver bene digerito la trasformazione galileiana è un assurdo. Soprattutto perché essa sarà confrontata con la sua trasformazione equivalente valida SEMPRE, quella di Lorentz. Torniamo a noi…

La relazione precedente esprime il principio galileiano (e poi anche newtoniano) di addizione di velocità. Sembra una sciocchezza, ma solo attraverso di lei è stato possibile sviluppare tutta la meccanica classica…

Possiamo anche permetterci di generalizzare la relazione di prima che, come avete notato, si riferisce solo ai moduli della velocità. L’abbiamo potuto fare perché le velocità erano tutte dirette nella stessa direzione. Tuttavia, la velocità v di P può essere diretta comunque, come rappresentato in Fig. 3.

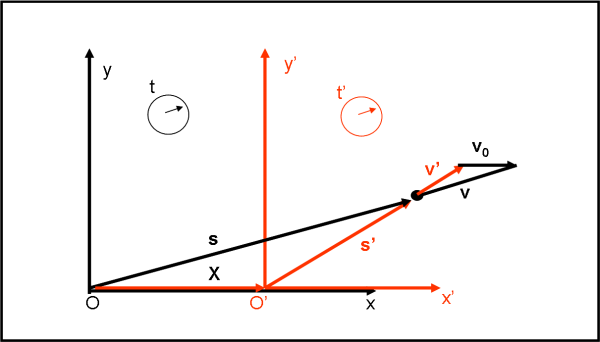
Abbiamo qualche problema a risolvere questa situazione apparentemente più complicata. Assolutamente no, perché sappiamo bene come trattare i vettori e la velocità è un vettore. Indichiamo come vettori anche le distanze tra i punti che ci interessano.

Consideriamo il vettore X che definisce lo spostamento di O’ rispetto a O.  Poi, il vettore s’ che indica lo spostamento di P rispetto ad O’. Chiamiamo s il vettore spostamento di P rispetto a O. Sappiamo benissimo sommare vettorialmente i vettori attraverso la regola del parallelogramma, ossia rappresentare graficamente l’espressione

s = s’ + X

nella Fig. 6. Non ci resta, adesso, che derivare questa relazione rispetto al tempo e ottenere le velocità (variazioni del vettore spostamento rispetto al tempo). Abbiamo:

ds/dt = ds’/dt + dX/dt, ossia:

v =  v’ + v₀      …. (3)

Come era ovvio attendersi, le velocità si sommano vettorialmente: date due velocità si trova la loro somma attraverso la regola del parallelogramma. Il principio di addizione delle velocità continua ad essere valido. Il caso precedente era, ovviamente, solo un caso particolare.

La fisica non cambia

Vediamo, adesso, come questa semplice constatazione porti immediatamente a dimostrare che le leggi della fisica rimangono le stesse in sistemi inerziali. Non l’abbiamo mai detto espressamente (forse), ma sappiamo molto bene che le accelerazioni non sono altro che variazioni infinitesime delle velocità rispetto al tempo. In altre parole, l’accelerazione è la derivata della velocità. Proviamo, allora a derivare la relazione (3) che descrive il principio di addizione delle velocità e vediamo quello che capita:

dv/dt = dv’/dt + dv₀/dt  … (4)

Ovviamente, se la velocità impartita al punto P fosse una costante, tutto andrebbe a zero. Conclusione ovvia, dato che un ulteriore velocità costante farebbe solo passare a un nuovo sistema inerziale. A noi interessa, invece, che avvenga un fenomeno fisico che segua le leggi della dinamica. Imponiamo, allora, come già detto prima, che la velocità  v’ non sia costante, ossia vari per effetto di un’accelerazione. Ovviamente, varierà anche v.

Ne segue che dv/dt = a   e dv’/dt = a’

dv₀/dt è invece la derivata di una costante e non può che valere ZERO. La relazione (4) diventa soltanto:

a = a’  …. (5)

Questa uguaglianza ha un’importanza fondamentale se collegata al secondo principio della dinamica di Newton, che dice che una forza è data dal prodotto tra la massa e l’accelerazione. Assumendo, e Galileo e Newton lo potevano fare, che la massa sia una costante rispetto al tempo (non lo sarà più per Einstein), la relazione  (5) ci dice che vale anche:

ma = ma’

ossia:  F = F’

In parole molto semplici: in sistemi inerziali le forze si eguagliano, ossia i fenomeni fisici (che derivano solo dalle forze) sono invarianti. O ancora: le leggi della fisica sono invarianti rispetto alle trasformazioni di Galileo.

Questa conclusione ci dimostra perché sia Simplicio che Salviati vedono la pallina cadere nello stesso modo per effetto della gravità nei loro due sistemi di riferimento (quello interno e quello esterno alla carrozza). L’accelerazione di gravità è la stessa in entrambi i sistemi di riferimento e tale è anche la legge del moto.

Ognuno la vede a modo suo

Vogliamo fare un passetto in più, a livello di fisica classica? Immaginiamo che la carrozza di Simplicio subisca un’accelerazione, ossia un cambiamento di velocità. Attenzione: questa assunzione fa crollare l’uguaglianza delle forze, dato che i sistemi non sono più inerziali.

La (4) diventa:

a = a’ + dv₀/dt = a’ + A

A non è più zero dato che v₀ non è più costante!

Cosa vede Salviati nel suo sistema di riferimento? Per lui non cambia “quasi” niente. Vede cadere la pallina sul pavimento e poco gli importa che la pallina parta quando è vicino alla parete frontale e arrivi sul pavimento nella zona posteriore della carrozza. Il suo sistema di riferimento è fisso e il moto viene descritto attraverso una caduta libera sotto un’unica forza verticale, quella peso, come mostra la Fig. 4. In due tempi successivi, la distanza della pallina dall’asse delle x è rimasta costante.

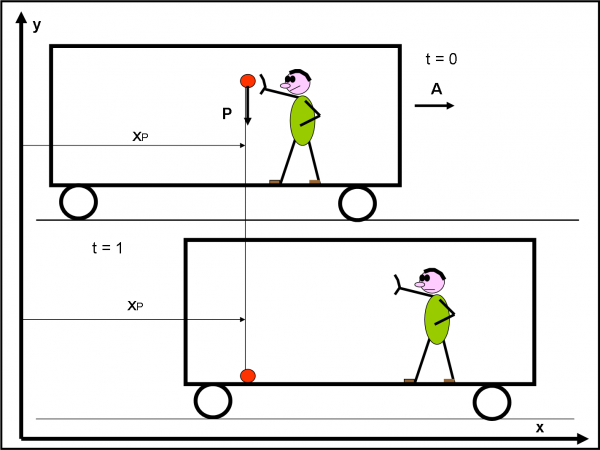
Cosa vede, invece, Simplicio? Per lui il vagone è fermo e vede la pallina cadere in diagonale, muovendosi verso la parte posteriore del treno, come se quest’ultima l’attirasse a lei (Fig. 5). Non può certo descrivere il moto come Salviati. È costretto a introdurre una forza fittizia (che si somma alla forza peso)  per non uscire pazzo. Lui conclude che sulla pallina agisce sia la gravità che una forza diretta verso la parete di fondo che vale proprio F = -mA. La risultante delle forze è la forza D che trascina la pallina fino al pavimento. La legge del moto deve essere cambiata affinché il risultato finale sia sempre lo stesso.

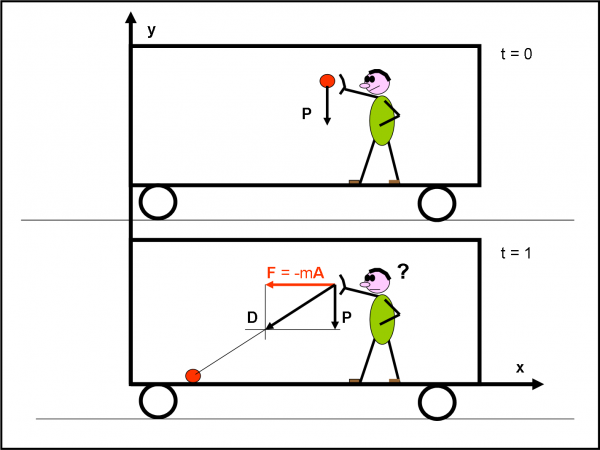
Facciamo ancora qualche piccola riflessione: In realtà Salviati si accorge che la carrozza sta accelerando, ma il suo sistema di riferimento è fisso e non subisce l’accelerazione. Rispetto ai suoi assi cartesiani la pallina DEVE subire solo la forza peso, dato che non è assolutamente legata all’accelerazione della carrozza (lei cade senza risentirne affatto). Tuttavia, Salviati nota benissimo che le pareti della carrozza si sono spostate e che la pallina nella sua caduta verticale giunge a terra in punto più vicino alla parete posteriore. Lui, però, non ha bisogno di spiegare questo spostamento, dato che deve solo descrivere ciò che fa la pallina e lei cade in modo perfettamente verticale. Se fosse intelligente, come realmente è nel “Dialogo”, capirebbe, però, perfettamente che la carrozza sta accelerando.

Simplicio, invece, si considera, ovviamente, fermo, così come considera ferme le pareti. Per lui, allora, il movimento della pallina non è affatto verticale, ma “diagonale” e ciò implica, per lui, l’introduzione di una forza aggiuntiva, in qualche modo fittizia, ma più che reale per la pallina! Lui dovrebbe essere piuttosto intelligente per capire cosa succede, realmente, visto dal di fuori.

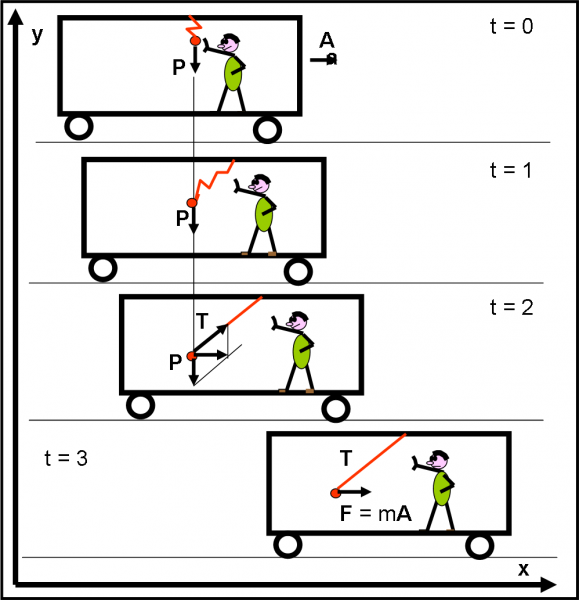
Un equilibrio “quasi” perfetto

Complichiamo ancora un poco le cose. Leghiamo la pallina al soffitto attraverso una corda più corta dell’altezza della carrozza. Iniziamo da ciò che vede Salviati in Fig. 6. Spezziamo l’azione in quattro tempi. Al tempo 0 la pallina viene lasciata cadere. Al tempo 1 la pallina sta ancora cadendo normalmente in verticale, anche se si trascina dietro la corda rossa. Salviati, vede, comunque, che la pallina si è spostata rispetto al punto in cui la corda è legata al soffitto. Al tempo 2 la corda si tende e la pallina smette di cadere. Questa situazione resta immutata al tempo 3: la corda è piegata rispetto al vagone. Cosa conclude Salviati? Capisce che la corda agisce sulla pallina con una forza T che la trattiene. Basta che sommi le due forze agenti sulla pallina per concludere che su di lei agisce  una forza orizzontale F = mA, dove A è proprio l’accelerazione a cui è soggetta la carrozza. In parole povere, la pallina è “bloccata” dalla tensione della corda e dalla forza peso, ed è trascinata nel moto accelerato della carrozza.

Simplico è invece piuttosto sorpreso (come sempre…). Per lui, dopo che la pallina ha cominciato a cadere diagonalmente per effetto della forza risultante, nel momento in cui la corda si tende al massimo... tutto si immobilizza. La pallina si ferma ad una certa altezza dal pavimento e non cambia più posizione La pallina risulta perfettamente immobile. E’ di fronte a un perfetto equilibrio. Non può fare altro che introdurre una forza T che sia uguale a contraria alla forza D (somma di F e di P). Nel suo sistema di riferimento tutte le forze si sono annullate tra loro (Fig. 7)

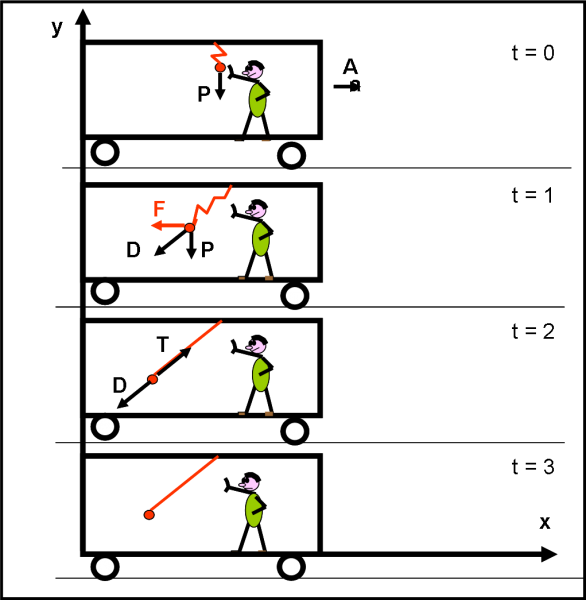
Tuttavia, notiamo bene che l’evento che è capitato è uno e uno solo. Cambia solo il modo di rappresentarlo!

Vorrei ancora farvi notare come a partire da una semplicissima relazione che lega le coordinate di due sistemi inerziali, si sia riusciti a trovare il legame tra le velocità e le accelerazioni. Non solo, però. Su queste basi è stato possibile esprimere e comprendere la variazione delle leggi del moto in sistemi NON inerziali e le motivazioni delle cosiddette forze fittizie. Come già detto, Galileo ha dato il via alla fisica moderna e Newton l’ha estesa a tutta la realtà “umana”.  Pensiamoci bene... Chi ha compiuto la più grande rivoluzione? L’accoppiata Galileo-Newton che ha costruito la dinamica a partire praticamente da zero, portandoci sulla Luna e magari su Marte, o l’accoppiata Einstein-Lorentz che l’ha solo modificata per adeguarsi a velocità troppo alte per la vita quotidiana?

Sto ovviamente scherzando, dato che la scienza non si misura con il metro. Sappiamo ormai troppo bene che la velocità diventa veramente alta nel mondo del microcosmo, quello da cui tutto è partito e che tutto regola. Tuttavia, guai a noi a considerare la fisica classica come un qualcosa retrocessa  in serie B. E guai a noi se volessimo saltarla a piè pari ed entrare immediatamente nel paese di Alice. Prima o poi ci presenterà il conto! Ricordiamoci che lo stesso Einstein è partito proprio dalla relatività galileiana, nutrendo il lei un profondo rispetto e modificandola quasi con timore.

 

QUI tutti gli articoli sulla Relatività Galileiana