Gli elettroni devono tenersi a distanza

Ne scegliamo uno semplicissimo, che mostri tutte e tre le lettere fondamentali. Descriviamo accuratamente l’evento che vogliamo rappresentare e poi disegniamolo attraverso le lettere appena imparate. Vogliamo calcolare la probabilità che due elettroni, posti in 1 e 2, finiscano nei punti 3 e 4 del foglio spazio-tempo. L’evento, partire sia da 1 che da 2 e finire sia in 3 che in 4, può compiersi ovviamente, in molti modi. Noi però, conosciamo le ampiezze delle lettere corrispondenti e non abbiamo alcun problema a descriverli uno alla volta. L’evento ci ricorda quello che avevamo descritto con i fotoni per introdurre la moltiplicazione nel caso di un evento composto da due eventi che capitano in concomitanza (articolo 9), ricordate? Ma, allora, disegnavamo SOLO nello spazio, ora nello spazio-tempo.

Iniziamo con le strade più semplici, come mostrato in Fig. 52(a).

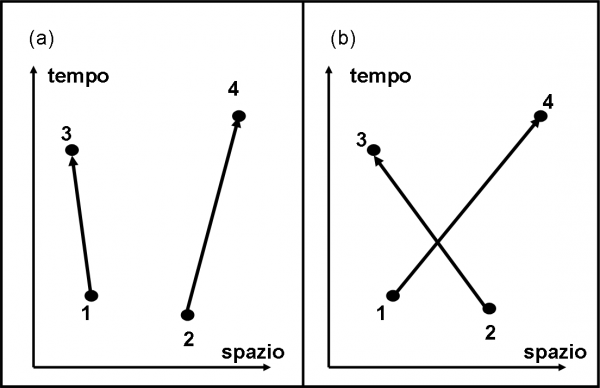
Un elettrone parte da 1 e arriva in 3. L’altro elettrone parte da 2 e arriva in 4. L’evento è verificato. Qual è l’ampiezza di probabilità dell’evento completo seguendo questa strada? Basta moltiplicare tra loro le ampiezze dei due sotto-eventi. L’ampiezza finale per questa prima via è quindi data da E(1,3) x E(2,4). Banale direi? Ricordiamoci sempre, però, che dire da 1 a 3 vuole dire descrivere un numero incredibile di vie alternative con un numero enorme di possibili “step” intermedi e cambi di direzione. La freccia 1-3 è un simbolo per rappresentare tutta questa enorme serie di possibilità, che, tuttavia, sono tenute in conto nella formula che descrive E(1,3). Non lo diremo più, ma non pensiamo che la freccia da 1 a 3 indichi solo una strada dell’elettrone. Tuttavia, disegnandolo in questo modo, ogni elettrone non ha accoppiamenti lungo il suo percorso, comunque sia complicato e travagliato.

E’ immediato trovare una seconda strada altrettanto semplice: un elettrone parte da 1 e finisce in 4 e l’altro parte da 2 e finisce in 3 (Fig. 52(b)). L’evento è nuovamente verificato. Quanto vale la sua ampiezza di probabilità? Presto detto: E(1,4) x E(2,3).

Se volessimo fermarci qui, non ci resterebbe adesso che sommare vettorialmente le due ampiezze e avremmo l’ampiezza finale dell’evento. In linea di massima, l’ampiezza di probabilità ottenuta con queste due “ovvie” strade (e di conseguenza la probabilità che si verifichi l’evento) approssima più che bene la realtà dei fatti. Ci si potrebbe anche accontentare…? No, no, non scherziamo. Conosciamo benissimo le possibilità della QED e non possiamo fermarci a una prima “rozza” approssimazione: la Natura a volte è capricciosa e su spazi piccoli ne combina di tutti i colori. Dobbiamo andare avanti.

Finora abbiamo usato solo la seconda lettera dell’alfabeto (un elettrone va da un punto a un altro): è ora di introdurre anche le altre due. Presto fatto, basta aggiungere un fotone e due accoppiamenti elettrone-fotone. La nuova strada è descritta in Fig. 53(a)

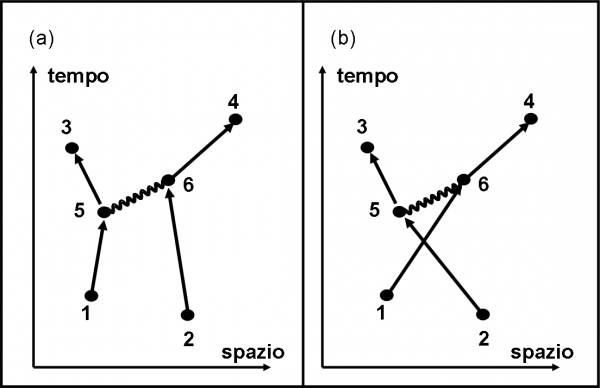
Cosa succede? Il primo elettrone, giunto a un certo punto (se ne stava andando in una direzione veramente qualsiasi?) emette un fotone e cambia direzione in modo da finire in 3. La stessa cosa fa il secondo elettrone. Anche lui subisce un accoppiamento. In questo caso, però, assorbe un fotone, proprio lo stesso emesso dal primo elettrone. Anche il secondo elettrone cambia direzione e finisce in 4. L’evento è verificato? Sicuramente sì, dato che gli elettroni sono giunti nei loro punti di arrivo. Notiamo che il fotone è apparso ed è sparito prima della conclusione dell’evento. Notiamo anche la differenza tra la possibilità dell’elettrone di cambiare percorso quante volte vuole (fatto richiamato nella figura precedente) e l’introduzione di un punto di accoppiamento. Non sono la stessa cosa, dato che nel secondo caso esiste una particolare ampiezza da associare a quel punto, indicata dal numero j.

Vogliamo calcolare l’ampiezza di probabilità finale di questo modo di verificare l’evento? Non è troppo difficile, anche se un po’ noioso. Non ci resta che moltiplicare tra loro le ampiezze di ogni azione svolta (le lettere) per completare l’evento. Scriviamo insieme questa moltiplicazione, ricordandoci che esiste anche il tragitto del fotone da 5 a 6. Non possiamo dimenticarcelo anche se il fotone ha solo fatto una fugace apparizione.

E(1,5) x j x E (5,3) x E(2,6) x j x E(6.4)x P(5,6)

Un bel pasticcio, pieno di accorciamenti e di rotazioni, che non vogliamo certo descrivere in dettaglio. Ormai c’interessa solo l’ampiezza di probabilità finale. Ricordiamoci, inoltre, che E e P sono espressioni matematiche non certo facili da scrivere. Tuttavia, noi lavoriamo solo graficamente, un’azione veramente elementare utilizzando le lettere di Alice. Conoscendo le ampiezze relative, la moltiplicazione ci permette di scrivere perfettamente la prima parola. Il risultato finale è stato ottenuto quasi ridendo e adesso ai “teorici” non resta che trasformarlo nuovamente in termini matematici. Anche loro, però, ne hanno approfittato, dato che non hanno dovuto fare tutti i conti intermedi, che sono stati sostituiti da poche linee tracciate su un foglio (ma quel foglio particolare, mi raccomando!).

Non è certo difficile inventarsi un’altra strada che verifica l’evento, come ad esempio mostra la Fig. 53(b). Siete sicuramente in grado di scrivere da soli l’espressione dell’ampiezza finale di questa strada e vi invito a provarci.

Cosa abbiamo trovato? Beh… che le due nuove strade portano anch’esse alla realizzazione  dell’evento e non sono assolutamente distinguibili dalle prime due della Fig. 52. Ognuna è una strada plausibile che ha una sua ampiezza di probabilità di essere seguita. E’ quindi è più che giusto sommarle vettorialmente alle prime due in modo da approssimare sempre meglio la probabilità totale dell’evento che, ricordo ancora, dice soltanto: due elettroni partono da 1 e 2 e finiscono in 3 e 4.

Attenzione a non dimenticarci che i punti 5 e 6 possono essere ovunque nello spazio-tempo e che spostando loro cambiano di conseguenza le espressioni che forniscono l’ampiezza di ogni nuova strada. Nuova strada vuol dire una nuova ampiezza finale alternativa da aggiungere a quelle precedenti. Un lavoro incredibilmente lungo e laborioso per essere completato manualmente!

Il fatto che 5 e 6 possano trovarsi ovunque, però, ci obbliga a fare un’importante riflessione a cui avevamo già accennato.

Se il punto 6 ha una coordinata tempo più grande di quella di 5 (ossia se il punto 6 è successivo al punto 5) preferiamo dire che il fotone è emesso in 5 e assorbito in 6. Se, invece, il punto 6 precede 5, preferiamo dire che il fotone è emesso in 6 e assorbito in 5. Tuttavia, potremmo anche dire, nel secondo caso, che il fotone è emesso in 5 e assorbito in 6, andando indietro nel tempo. Nel foglio di Alice niente è impossibile e quindi è meglio dire, in generale, che il fotone è stato scambiato dai due elettroni. A questo fotone così scambiato, che in realtà appare e scompare durante l’evento, viene dato il nome di fotone “virtuale”. Niente a che vedere con i fotoni virtuali che avevamo introdotto per cercare di esprimere il concetto relativo alla posizione qualsiasi che può assumere un fotone una volta che è partito da una sorgente. Notate anche che non ci siamo certo preoccupati di vedere come è inclinata la retta descritta dal fotone “virtuale”: può anche non essere a 45° e quindi muoversi a velocità diversa da c.

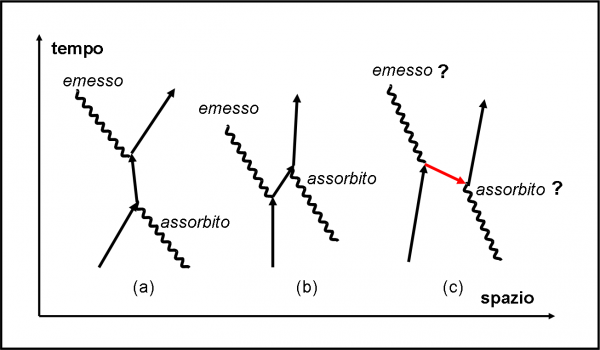
Vale la pena disegnare la Fig. 54, che illustra meglio questa situazione apparente assurda, ma del tutto ammissibile nel quaderno di Alice.

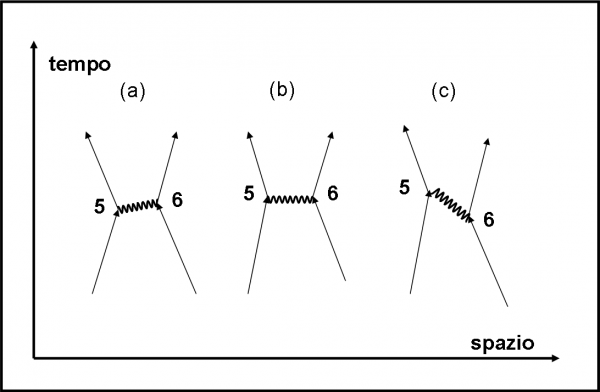
A sinistra (a) il caso più semplice: il fotone va nel verso giusto del tempo, anche se la sua velocità è maggiore di quella convenzionale. Nel secondo caso (b) il fotone è emesso e assorbito nello stesso istante (velocità infinita?). Nel terzo caso (c), la luce sembra andare secondo la sua velocità “normale”, ma lo fa nel verso opposto del tempo! Niente di strano, amici miei: siamo o non siamo nel regno dello Stregatto e del cappellaio matto? Possiamo dire che le ampiezze di probabilità che stiamo usando tengono conto di tutte queste possibilità e non vi è nessun problema a eseguire calcoli che sembrerebbero assurdi. In fondo, non fanno altro che seguire la Natura, dato che si ottengono proprio i suoi risultati!

Ci sembra di aver complicato abbastanza le cose? Nemmeno per sogno. Lo stesso evento ha infinite altre possibilità di verificarsi. Basta, ad esempio, aggiungere due ulteriori punti (7 e in cui avviene un nuovo scambio di un fotone virtuale tra i due elettroni. La Fig. 55 non è certo complicata, ma… le moltiplicazioni cominciano a diventare pesanti… anche perché 5,6,7,8 possono essere ovunque. Milioni e milioni di vie alternative che si devono sommare. Mamma mia… Se volete, potete provare a scrivere l’ampiezza di probabilità di questa figura: è solo un lavoro di routine quantistica!

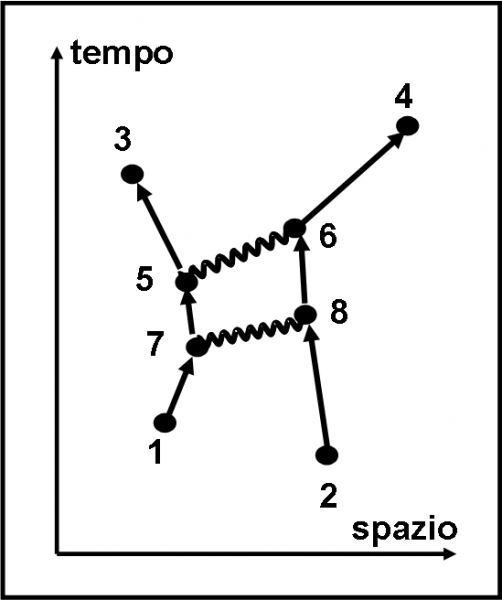
A mano a mano che continuiamo a complicare le cose, risulta evidente una particolarità che ci aiuta non poco. Le prime due strade considerate per verificare l’evento non fanno uso di accoppiamenti, ossia manca sia la seconda che la terza lettera dell’alfabeto. Ne consegue che non compare il numero “magico” j. Aggiungendo due punti intermedi e un fotone, compare il numero j x j. Nel caso dei quattro punti intermedi (due fotoni virtuali) il numero diventa j x j x j x j.

Ricordiamo, però, che ogni j implica un accorciamento dell’ampiezza a circa 0.1. La strada con due punti porta, quindi, a un’ampiezza ridotta a 0.1 x 0.1 = 0.01, rispetto a quella senza accoppiamenti. Con quattro punti l’ampiezza si riduce a 0.1 x 0.1 x 0.1 x 0.1 = 0. 0001 (ossia uno su 10000). Se avessimo tempo al computer potremmo arrivare fino al caso di  j ⁶, con tutte le possibili posizioni dei 6 punti aggiuntivi. Cosa stiamo imparando? Che questo metodo di calcolo della probabilità di un evento non ha nessun problema di arrivare fino a una precisione fantastica: basta continuare con una regola sempre uguale e oltremodo semplice concettualmente. Se mai ce ne fosse bisogno, una prova ulteriore della perfezione della QED.

Per cercare di rimanere con i piedi per terra, cosa significa ciò che abbiamo appena visto? Molto facile da tradurre in parole “comuni”: due elettroni si inviano un’informazione tramite un fotone. Quest’ultimo è il messaggero, un mediatore della forza che si esercita tra le due particelle che capiscono di doversi tenere a distanza. Due elettroni non possono attrarsi ma respingersi. Il fotone virtuale evita uno scontro “impossibile”.

Io  do un fotone a te e tu dai un fotone a me: lo scattering della luce

Presentiamo, ora, un altro evento descritto facilmente dal diagramma relativo. Iniziamo con un elettrone e un fotone e terminiamo ancora con un fotone e un elettrone. Tra le tante strade possibili per verificare l’evento, ce ne interessa una in particolare che introduce due volte la terza lettera. In realtà potevamo anche far continuare fotone ed elettrone senza alcun incontro, ma sarebbe  una strada di poco interesse scientifico, anche se molto più probabile. Nel caso prescelto l’elettrone assorbe il fotone e, dopo un po’, lo riemette di nuovo. L’evento è verificato e il diagramma descrive perfettamente quello che chiamiamo normalmente “scattering” della luce. Cominciate a capire la grandezza dei diagrammi di Feynman? Definite le ampiezze di probabilità delle tre lettere di base, la loro combinazione porta a descrivere tutti i fenomeni della Natura.

La Fig. 56 illustra il caso in oggetto: in (a) l’elettrone assorbe un fotone, continua da solo e dopo un po’ emette un altro fotone. L’evento è verificato dato che siamo partiti da un fotone e un elettrone, in un certo istante, e siamo arrivati ancora con un fotone e un elettrone, in un tempo successivo. Tuttavia, si possono presentare altre possibilità. In (b) l’elettrone emette prima un fotone e poi ne assorbe un altro. Come sappiamo, le due azioni sono equivalenti. In (c), però, le cose si complicano un poco (per noi almeno). L’elettrone emette un fotone, poi torna indietro nel tempo per assorbire un altro fotone e infine riprende il cammino normale. L’evento è verificato nuovamente, anche se abbiamo avuto bisogno di un’azione apparentemente molto strana (che però è tenuta in conto nella formula che rappresenta E(A,B)). Discutiamone un attimo.

Antimateria

L’elettrone così “anomalo”  ha una caratteristica saliente, malgrado sia del tutto identico a un elettrone normale: esso viene attratto da quest’ultimo e si definisce come elettrone a carica positiva (se sviluppassimo la formula della probabilità tenendo conto della polarizzazione ce ne renderemmo conto attraverso il segno di j… ma è troppo per noi e accettiamo questo strano comportamento senza crearci problemi inutili). In altre parole, prende il nome di positrone o anti-elettrone. Ogni particella ha una sua anti-particella, tranne il fotone che è l’anti-particella di se stessa. Lo abbiamo già visto precedentemente, quando il fotone tornava indietro nel tempo, ma niente cambiava dato che emissione e assorbimento sono la stessa cosa. Quando un elettrone e un positrone si incontrano si annichiliscono dando origine ad almeno un fotone.

Ricordiamo solo che tutte le particelle, tranne appunto il fotone, hanno un’anti particella. Ogni riferimento all’antimateria NON è assolutamente casuale!

Si potrebbero usare due modi per indicare un positrone: o si lascia la freccia direzionale così com’è, accettando che sia un elettrone che va indietro nel tempo, o si cambia il senso della freccia direzionale, sapendo però che siamo di fronte a una nuova particella, il positrone appunto. Noi useremo la prima, dato che ci permette di vedere subito se la particella è a carica positiva o negativa: basta vedere se il suo verso è opposto o pure no a quello del tempo.

Sì, sì, tante belle parole… ma vorremmo capire come il diagramma di Feynman ci descrive queste azioni (confermate dagli esperimenti di laboratorio e quindi naturali). Riprendiamo la Fig. 56(c) e riproponiamola in Fig. 57, dividendola, per facilitare il discorso, in intervalli temporali (linee orizzontali).

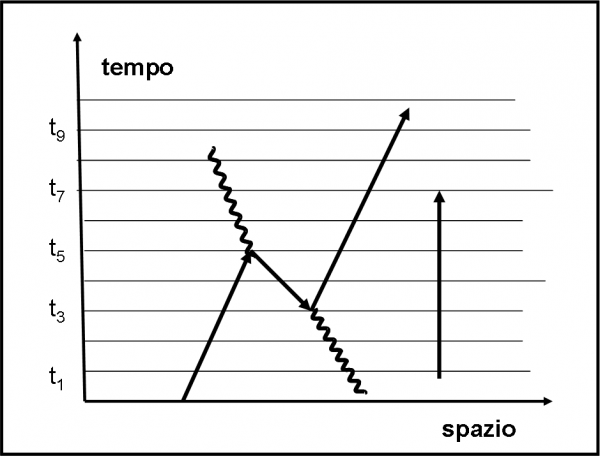
Muoviamoci nella direzione positiva del tempo, ossia verso l’alto, come siamo abituati a fare nel nostro mondo, non cercando di guardare troppo avanti, ma descrivendo quello che ci appare di volta in volta. In parole povere non sappiamo se un elettrone nel futuro ha assorbito o emesso un fotone ed è tornato indietro. Noi conosciamo quello che vediamo. In t₀ troviamo un elettrone e un fotone che si muovono uno verso l’altro nella giusta direzione temporale. Tutto prosegue normalmente fino a t₃, quando improvvisamente il fotone si trasforma in due particelle, un elettrone e un positrone (a prima vista potrebbe anche sembrare un elettrone, ma ha verso opposto). Il positrone continua la sua corsa, ma non riesce a vivere a lungo e si incontra con l’elettrone in t₅ (che è poi se stesso!) annichilendosi e dando origine a un fotone, che continua verso l’alto, così come sta facendo anche l’elettrone “creatosi” in t₃. In t₇ tutto è a posto: un elettrone e un fotone, come previsto dall’evento. Questa è una visione “normale” del fenomeno, che, però, può essere interpretato come un doppio accoppiamento secondo le regole generali esistenti nel piano di Alice, dove il verso del tempo non è assolutamente un ostacolo. L’evento che in questa visione è inteso come un’emissione, seguito da un assorbimento, nel tempo “comune” porta al fenomeno dell’annichilazione di un positrone e di un elettrone.

Ricordiamo ancora che questa sequenza è stata osservata in laboratorio ed è inserita nell’ampiezza E(A,B). Inoltre, teniamo conto che le anti-particelle sono rappresentate con un verso contrario a quello del tempo solo nel nostro foglio speciale. Non prendiamola come una “verità”: è solo un azione perfetta per il calcolo, ma del tutto simbolica. Siamo o non siamo nel mondo di Alice?

Un passo indietro

Forse siamo andati un po’ troppo veloci ed è meglio soffermarsi ancora sull’accoppiamento, ossia sulla terza lettera. Diciamoci la verità: se non ci fosse lei la Natura sarebbe veramente monotona e gli elettroni e i fotoni se ne andrebbero per i fatti loro senza mai incontrarsi. Anzi, ancora peggio, non ci sarebbero nemmeno gli oggetti, dato che le particelle non avrebbero modo di parlarsi e di formare atomi e cose sempre più complesse. La terza lettera, quindi, è proprio il sale dell’Universo! Essa, da sola, può già mostrare i primi diagrammi di Feynman che descrivono fenomeni che ben conosciamo. Innanzitutto, essa è valida solo se vi sono tre linee incidenti, due per l’elettrone e una per il fotone. Dato che l’elettrone deve essere unico, non potremo mai avere due elettroni entranti nel “punto triplo”. L’elettrone deve proseguire il suo cammino senza curarsi se va dalla parte del tempo positivo o negativo. Nel primo caso tutto è normale; nel secondo si ha, in realtà, l’unione è l’annichilimento di un elettrone e un positrone. Questa è la sola regola da ricordarsi perfettamente. Ossia, non cerchiamo MAI di disegnare due elettroni che entrano nel punto d’accoppiamento. Questo è un fenomeno assurdo anche per il mondo d’Alice. D’altra parte è ovvio. Vorrebbe dire che due elettroni possono attrarsi! Eh no! Lo possono fare solo un elettrone e un positrone.

Vediamo in Fig. 58 alcuni casi di accoppiamento, di cui due sono assurdi anche per il mondo dell’assurdo.

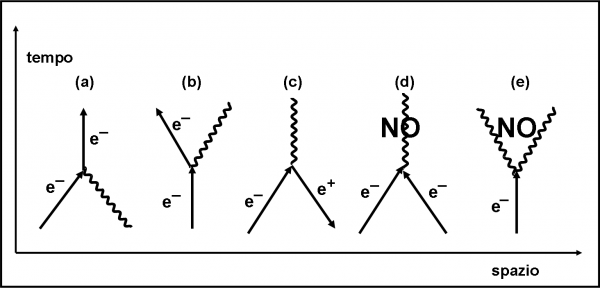
La (a) ci mostra un elettrone che assorbe un fotone e continua indisturbato verso l’alto. Perché diciamo che il fotone è stato assorbito? Ovvio, perché esso scompare andando verso il tempo positivo. Una particella è stata “ingoiata"! Questo semplicissimo digramma corrisponde a qualcosa che conosciamo? Sicuramente sì. pensate a un’antenna radio che capta i fotoni in arrivo o a una lente o a un semplice pezzo di vetro, ecc., ecc.

In (b), invece, partiamo con un elettrone che nel punto critico tira fuori un fotone dal suo cappello. Abbiamo cominciato con una sola particella e finiamo con due. In questo caso si è creato un fotone e quindi è stato “emesso”. Conosciamo questo fenomeno? Beh… basta pensare ai colori! La (b) però potrebbe anche essere interpretata come assorbimento di un fotone particolare, ossia un fotone che torna indietro nel tempo. Dato che l’antifotone rimane se stesso la faccenda non ci sconvolge di certo e l’abbiamo già visto nel caso del fotone “virtuale” che permette a due elettroni di comunicare e di avvisarsi che è meglio tenersi alla larga uno dall’altro (Fig. 54).

Il caso (c) è quello apparentemente più strano. Si ottiene, però, attraverso semplici ribaltamenti di figura (non approfondiamo se no cadiamo nella simmetria CPT e non la finiremmo più). Anche in questo caso vi è l' elettrone entrante e  uscente, ma quest’ultimo va indietro nel tempo e quindi è un positrone. In realtà, quindi, abbiamo un elettrone e un positrone entranti nel punto di interazione. Seguendo il verso positivo del tempo, partiamo, quindi, con un elettrone e un positrone e finiamo solo e soltanto con un fotone. La particella e l’antiparticella hanno subito l’annichilimento.

Il caso (d) non è invece ammissibile. In esso si parte con due elettroni che convergono in un punto. No, impossibile e quindi la terza lettera è stata scritta in modo errato. La stessa cosa capita in (e) dove compare un solo elettrone e due fotoni. No, niente da fare. Rimandati a settembre!

Bene, direi che l’interazione o accoppiamento sia stato analizzato da ogni parte e non dovremmo più avere problemi a comprenderla nei diagrammi più complicati. Ci ha anche permesso di descrivere come compare l’antimateria nel mondo di Alice: è solo questione di direzione, dato che nel nostro foglio speciale si può andare dove si vuole rispetto al tempo.

Qualcuno starà, forse, pensando alle leggi di conservazione… Infatti, abbiamo visto che si distruggono e si creano particelle dal niente. Si parte con una e si arriva a due e viceversa. Ani può capitare molto di peggio con diagrammi più complicati come vedremo tra un attimo. Nessuna paura. La matematica risolve tutti i problemi relativi (fidatevi), ma nei diagrammi l’importante è che si conservi la “carica” totale delle particelle. Se, in un vostro diagramma doveste trovare che la carica è cambiata… fermatevi perché avete commesso un errore.

Tanto per prendere dimestichezza (ma senza spiegare cosa significhi) ecco, in Fig. 59, un diagramma molto più complesso (l’avremmo potuto disegnare a tentativi, per divertimento). Contiamo le cariche all’inizio: due elettroni veri, ossia due cariche negative. Vediamo cosa troviamo alla fine: tre elettroni e un positrone, ossia tre cariche negative e una positiva, ossia due cariche negative. Perfetto. Il diagramma ha sicuramente un senso e rappresenta un processo della Natura. Questa è la grande forza dei diagrammi di Feynman.

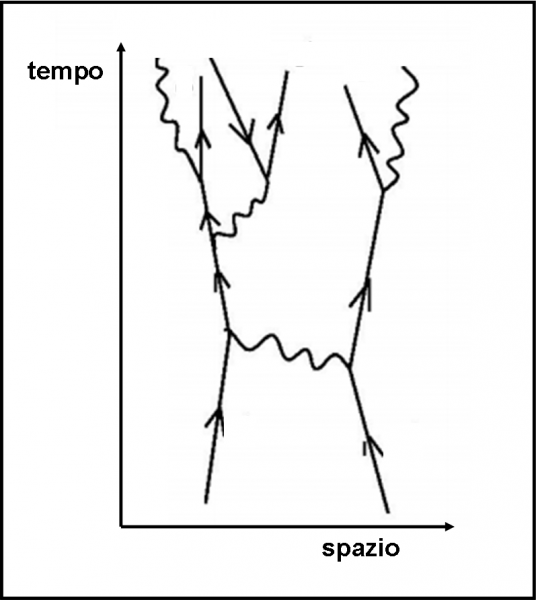
Teoricamente potremmo inventarci qualsiasi disegno, più o meno complicato, ma se rispettiamo le poche regole che conosciamo e se le cariche si conservano, siamo SICURI di aver rappresentato un fenomeno naturale, qualunque sia la sua ampiezza di probabilità di accadere (a quello ci pensano le ampiezze che si moltiplicano). E non dobbiamo nemmeno preoccuparci di quante particelle vi sono all’inizio e alla fine. Nel caso della figura partiamo con due e arriviamo addirittura a sei (oltre ad avere avuto un fotone virtuale durante il percorso).

Chiudiamo questo articolo con un momento di auto soddisfazione. Pensate, cari amici, che potreste facilmente costruire da soli diagrammi anche più complicati di quello appena mostrato. Basterebbe stare bene attenti al verso delle frecce e contare le cariche. A quel punto, in pochi minuti, avreste sottomano un fenomeno naturale che per poter essere descritto matematicamente passo dopo passo avrebbe avuto bisogno di una preparazione superiore e/o un tempo enorme al supercomputer. Invece, in pochi minuti si ottiene un risultato SICURAMENTE plausibile e possibile.

Basta, a questo punto, dare il vostro disegno a un matematico con i fiocchi (non a me…) e fargli trasformare il diagramma in linguaggio matematico. Vi darà la soluzione, evitando tutti i passaggi intermedi. Capite che meraviglia la QED? Un premio Nobel per la fisica quantistica potrebbe anche avere un assistente bambino (un po’ sveglio e riflessivo). Il giovane disegnerebbe diagrammi a piacere e lo scienziato non dovrebbe far altro che riscriverli con le formule relative, interpretarli e magari chiedere ai tecnici del CERN di effettuate un certo esperimento che verifichi quanto disegnato allegramente dal mini-assistente.

Va bene… ho un po’ scherzato, ma non poi tanto…

La prossima volta introdurremo l’atomo, ma le cose non cambieranno di molto. Ormai l’alfabeto lo conosciamo abbastanza bene per scrivere frasi sempre più lunghe e interessanti. Torneremo anche sulla famosa riflessione (ancora lei!) e capiremo molte cose…