La casa dell’elettrone

Abbiamo parlato di elettroni, considerandoli liberi di muoversi a loro piacimento, quasi come fossero dei… fotoni. In realtà, la situazione è piuttosto diversa. Gli elettroni sono normalmente (nei fenomeni più comuni) legati a un peso non trascurabile. In altre parole… hanno sempre una palla al piede che li tiene ancorati a un  qualcosa. Quel qualcosa è il nucleo atomico, dove si rifugiano i protoni e i neutroni, a loro volta “casa” di particelle ancora più piccole.

Feynman chiama il protone il “vaso di Pandora”: guai ad aprirlo! Al livello raggiunto finora possiamo permetterci di non complicare troppo le cose e considerare il nucleo atomico come una singola particella in quiete, ossia priva di movimento spaziale. Anche a lui si associa, ovviamente, un’ampiezza di probabilità di andare da un punto a un altro e l’espressione è del tutto simile alla E(A,B) dell’elettrone, solo che contiene un numero maggiore di “n” (ricordate?). Il nucleo è però ben più “pesante” dell’elettrone e non commettiamo un grave errore se lo consideriamo fermo.

Sempre per motivi di semplicità riferiamoci all’atomo più semplice, ossia a quello dell’idrogeno. Il nucleo si riduce a un protone ed è presente un solo elettrone. La Fig. 60 illustra il diagramma spazio-temporale di questo atomo.

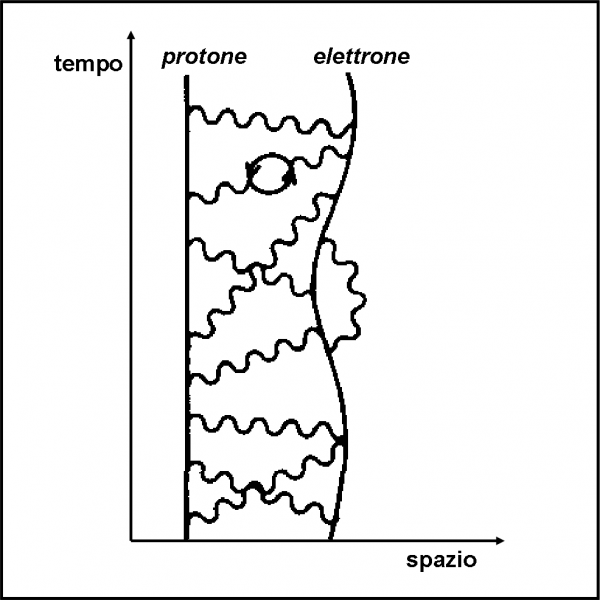
La linea verticale rappresenta il protone (non si muove nello spazio), mentre la linea ondulata è l’elettrone, che scalpita, ma che viene trattenuto a una certa distanza da un continuo scambio di fotoni virtuali con il protone. Un messaggio continuo, una mediazione della forza che tiene unito l’atomo. Un vero e proprio balletto che l’elettrone compie “attorno” al nucleo. Ovviamente, se il nucleo è composto da più protoni, gli elettroni aumentano e il diagramma corrispondente si complica in modo mostruoso, ma non per questo cessa di essere rappresentabile con le solite regole della QED. Ricordiamoci che le lettere dell’alfabeto rimangono solo e soltanto tre.

L’ampiezza di un fotone che viene scambiato tra protone ed elettrone è semplicemente (–j) x P(A,B) x j. In altre parole, l’ampiezza di un fotone che va da un punto a un altro, moltiplicata per le ampiezze dei due accoppiamenti. Il segno meno di j definisce quello relativo all’accoppiamento protone-elettrone. Non preoccupatevi di un fotone che esce ed entra nello stesso elettrone e nemmeno di quello strano cerchietto che individua la nascita e la morte simultanea di un positrone: possiamo trascurarli (almeno per adesso).

Se quello precedente è il diagramma relativo al mantenimento di un elettrone nei pressi del protone, non è difficile disegnare lo “scattering”  della luce quando l’elettrone è ancorato al suo atomo.  Lo vediamo in Fig. 61.

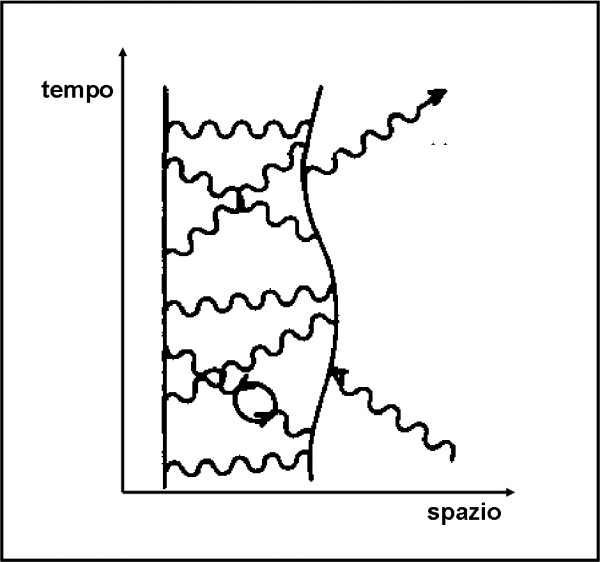
Mentre continua ad avvenire il continuo scambio di fotoni, un fotone estraneo può facilmente colpire l’elettrone ed essere assorbito. Dopo poco tempo, l’elettrone “sputa”un nuovo fotone, dando luogo al fenomeno di scattering. Può anche capitare (e l’abbiamo già visto) che l’elettrone emetta prima un fotone e poi l’assorba. Le varie combinazioni danno luogo a tutti  i fenomeni di scattering che conosciamo.

Possiamo concludere questa rapida analisi dell’atomo con una constatazione veramente semplice: l’ampiezza di probabilità di avere uno scattering (di qualsiasi tipo sia) è data da una serie di rotazioni e accorciamenti che può essere definita come Sc. Sapremmo benissimo (non è un vero problema) scrivere quest’ampiezza, che dipende, ovviamente, dal nucleo e da come si sistemano gli elettroni vicino a lui. In parole semplici, l’ampiezza varia da materiale a materiale. Finora ci siamo soprattutto “fissati” sul vetro (e continueremo a farlo), ma ogni materiale ha la sua propria ampiezza di scattering.

Un piccolo commento prima di proseguire: vi siete accorti come è diventato banale e intuitivo disegnare (qualitativamente) un atomo e le interazioni tra nucleo ed elettrone? Per non parlare dei fenomeni di scattering e di interazione elettromagnetica. Sì, d’accordo, per passare alla quantificazione è necessario tradurre tutto in formule matematiche, ma praticamente non vi sono problemi concettuali, dato che ogni lettera ha una sua ben definita ampiezza di probabilità. Basta solo moltiplicare e sommare, operazioni alla portata di chiunque… Potrei permettermi di dire che più si va avanti e più le cose sembrano semplificarsi. Lo stesso succede a scuola: è molto più difficile scrivere le prime lettere dell’alfabeto che, una volta imparatele molto bene, iniziare a scrivere delle parole e delle frasi a senso compiuto.

Un cronometro fittizio

Penso che uno dei concetti, che vi ha “disturbato” di più, sia stato quel cronometro che, associato a una freccia, la faceva girare in modo diverso a seconda del colore della luce. La sua importanza è fondamentale, dato che la direzione della lancetta ci permette di sommare o di eliminare ampiezze di pari lunghezza. Un po’ come fa la velocità con l’accelerazione. Due velocità uguali possono dar luogo a un’accelerazione diversa da zero (il moto circolare uniforme ce lo insegna).

Dover vedere questa caratteristica così importante rappresentata da un cronometro astratto che non esiste in Natura è una fatica mentale che viene mal sopportata anche nel mondo di Alice.  Ormai, però, siamo in grado di svelare cos’ è veramente questo cronometro e come funziona. Lo possiamo fare perché non ci spaventano più i diagrammi spazio temporali (almeno spero…).

Prima di iniziare, ricordiamoci ancora una volta di non confondere traiettorie spazio temporali con traiettorie soltanto spaziali. Quando avevamo illustrato la riflessione e la doppia riflessione, usavamo traiettorie inclinate. Può anche darsi che qualcuno abbia confuso, saltuariamente, gli angoli indicati dalla lancetta del cronometro con gli angoli fatti dalle traiettorie. Adesso, questo non è più possibile, dato che lo spazio si è ridotto a una retta e quindi tutti i movimenti spaziali avvengono su di essa. Rimane, invece, inalterata la direzione della freccia-ampiezza e l’angolo ad essa relativa. Le traiettorie che vedremo indicheranno, d’ora in poi, percorsi immaginari nello spazio-tempo, l’unico foglio in cui possono essere rappresentate le tre lettere di Alice.

Per svelare il mistero del cronometro, pensiamo un attimo a come abbiamo definito l’ampiezza P(A,B) del viaggio di un fotone da un punto a un altro. Abbiamo parlato di rotazione della freccia? Assolutamente no. Eppure, andare da A a B vuol proprio dire partire dalla sorgente e giungere in un certo luogo (lo specchio, il vetro, il rivelatore). Si è sempre detto che durante questo viaggio spaziale il cronometro continua a girare e adesso, improvvisamente, non ce ne importa più niente e concludiamo che passare da A a B non comporta nessuna rotazione della freccia-ampiezza P(A,B).

Forse qualcuno ci aveva già pensato e aveva trovato questo confronto del tutto assurdo, anche per il mondo di Alice. E avrebbe avuto sicuramente ragione. Non possiamo più nasconderci dietro la rappresentazione ingenua e simbolica del cronometro.

L’angolo della ampiezza, infatti, non dipende dallo spazio percorso e dal tempo impiegato a percorrerlo, ma solo e soltanto dall’istante in cui la luce lascia la sorgente. Ma come?! Ci crolla il mondo addosso (quello normale). Tanta fatica a parlare di differenza di traiettoria e adesso la trascuriamo completamente?

Pensiamo un momento a ciò che succederebbe se la rotazione dell’ampiezza venisse impartita subito, all’inizio del viaggio. Se le frecce partissero tutte assieme avrebbero tutte la stessa direzione. Niente e nessuno la potrebbe cambiare senza incontri strani durante il percorso. Che una freccia faccia un percorso più lungo o più corto non potrebbe modificarla. Tuttavia (state bene attenti!), esse viaggiano alla stessa velocità e, quindi, se voglio ricevere la luce di due fotoni sullo stesso rivelatore allo stesso medesimo istante (quello che capita in realtà), devo considerare, per loro, tempi di partenza diversi. Solo tempi di partenza diversi danno angoli diversi alla freccia.

Tuttavia, se voglio che due fotoni partano in tempi diversi (angolo di ampiezza diverso) e arrivino contemporaneamente nello stesso punto, è necessario che uno dei due faccia un percorso più lungo o più corto. In caso contrario (ossia percorsi spaziali uguali),  dato che la loro velocità è costante (e la possiamo considerare uguale a c su lunghe distanze),  uno dei due arriverebbe o prima o dopo l’altro. Da questa conclusione non si scappa neanche nel mondo di Alice.

Insomma, tempi di partenza diversi e arrivi simultanei implicano anche percorsi diversi: i due metodi di calcolo dell’angolo sono perfettamente equivalenti.

Non confondetevi… sto dicendo una vera banalità. Se due atleti vanno alla stessa velocità e voglio vederli arrivare sul traguardo nello stesso istante, facendoli partire in tempi diversi, è necessario che uno dei due faccia un percorso più lungo.  O, inversamente, se voglio che arrivino insieme, ma hanno davanti percorsi diversi, è necessario che partano in tempi diversi. Le due cose sono perfettamente uguali. Da questa semplice riflessione se ne deduce che non abbiamo commesso nessun errore finora a far girare la lancetta del cronometro: il risultato finale è lo stesso. Tuttavia, lo spazio-tempo e le lettere del nuovo linguaggio ci permettono, adesso, di essere un po’ meno assurdi nel mondo dell’assurdo.

Ancora la doppia riflessione (che barba!)

Bando alle ciance e a tante parole, vediamo cosa capita in realtà. L’evento da descrivere è: “Parti da S e arriva in R a un certo istante, dopo la riflessione  su una lamina di vetro ”. Come si vede, non parliamo più di doppia riflessione… non c’è più bisogno di semplificazioni artificiose (lo vedremo meglio tra poco). L’evento è, però, sempre lo stesso, lo conosciamo molto bene.

Iniziamo con analisi accurata della sorgente S. Restiamo nell’ambito di luce monocromatica, ossia di un solo colore. In queste condizioni, l’ampiezza di probabilità che un fotone venga emesso varia in modo regolare col tempo. In particolare, varia in modo regolare l’angolo della freccia. Cambiando colore, cambierebbe la velocità di variazione. Esattamente ciò che faceva il nostro cronometro “fittizio”. Se la luce fosse un mix di colori (ad esempio luce bianca) l’angolo cambierebbe in modo caotico, senza alcun regolarità. Nel caso di luce monocromatica, invece, è possibile sapere perfettamente come avviene la rotazione della freccia e quindi conoscere l’ampiezza di probabilità.

La faccenda è molto semplice: l’angolo varia  a velocità costante, esattamente come faceva quello della lancetta del cronometro, ma andando in senso inverso. La Fig. 62 ci mostra la situazione relativa alla sorgente S. Essa, ovviamente, non si muove e descrive, perciò, una retta verticale. In istanti successivi facciamo partire un fotone che descrive la sua traiettoria verso il rivelatore. La lunghezza della freccia di probabilità è sempre la stessa, ma l’angolo gira in verso antiorario, come illustrato nella parte sinistra del grafico. Notate che le traiettorie spazio temporali dei fotoni sono parallele, dato che su distanze grandi la velocità della luce può essere considerata costante e uguale a c (angolo di 45°).

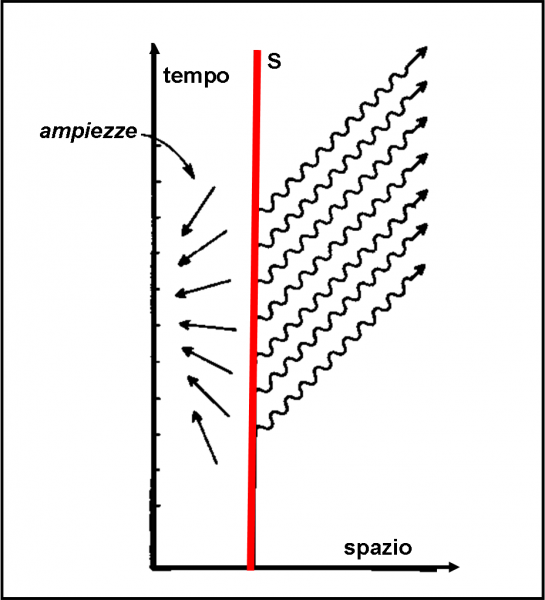
La luce è ora partita e viaggia verso la lamina di vetro. Non vi è più nessun cronometro e l’angolo dell’ampiezza rimane immutato fino al momento dell’incontro con il nuovo materiale. Non mi picchiate! Ricordo ancora che il viaggio e l’incontro successivo avvengono nello spazio-tempo e NON nello spazio come nei capitoli iniziali. Nello spazio attuale, tutto avviene lungo una direzione orizzontale costante.

Questa volta, ci conviene partire dal rivelatore R. L’importante, ricordiamolo bene, è che la luce emessa in tempi diversi arrivi allo stesso istante T. Questo fatto, come abbiamo già visto prima, è fondamentale. In quel momento il rivelatore deve fare “tic”. Lui riceve un solo fotone, ma la sua ampiezza di probabilità dipende dall’ampiezza di probabilità di tanti ipotetici “fotoni” inviati in tempi diversi da S. Capiamoci bene, però. E’ la solita vecchia storia che il fotone diventa fotone solo quando arriva, mentre prima è solo un ampiezza di probabilità.  Poco sopra avevo parlato di fotoni che partivano e arrivavano, solo per rendere più “comprensibile” la faccenda. In verità la situazione è ben diversa. A ogni istante ciò che parte da S sono ampiezze di probabilità che solo alla fine si combinano tutte assieme per descrivere la probabilità di avere un “tic” in un certo istante.

L’evento dice esattamente questo: “La luce parte da S, ma deve arrivare in R al tempo T” non una frazione di tempo prima o dopo. Vogliamo soltanto calcolare la probabilità che ha un fotone partito da S di arrivare in R al tempo T, ossia di fare “tic”. Quanto tempo ha a disposizione la sorgente per tentare di far accadere l’evento? Dipende… Da cosa? Dallo spessore della lastra di vetro, come vedremo prestissimo.

Ancora un attimo di pazienza… Finora abbiamo parlato di doppia riflessione della luce su una lamina di vetro e ci siamo limitati alla riflessione su due sole superfici, quella superiore e quella inferiore. In realtà ciò non è vero e adesso siamo in grado di dire veramente le cose come stanno. Ogni atomo di vetro concorre al fenomeno, in particolare i suoi elettroni. Essere capaci di descrivere lo scattering della luce con le nuove lettere ci permette di parlare seriamente e di evitare semplificazioni inutili. Le superfici non hanno alcuna importanza particolare.

Tutto il processo viene gestito dagli elettroni interni al vetro che continuano ad assorbire fotoni e a riemetterli. Tuttavia, il risultato è esattamente lo stesso, per cui la divisione in due superfici continua a essere un procedimento più che valido. Solo che tra poco sapremo perché possiamo permetterci di eseguire questa semplificazione.

Disegniamo la Fig. 63 e non spaventiamoci. Sembra complicata ma non lo è. Basta descriverla e seguirla con molta calma. Dividiamo la lamina di vetro in un certo numero di straterelli (sei, ad esempio). Facciamo anche una premessa. Da quanto abbiamo dedotto nelle prime lezioni, sappiamo che la luce è soprattutto riflessa nella parte mediana della lamina di vetro. Non solo, però. Sappiamo anche che la direzione che può prendere è o verso il rivelatore R1 o verso l’interno della lamina. Per ottenere questo risultato avevamo sommato frecce relative a percorsi diversi. Ricordate? Bene, questo risultato vuole anche dire che lo scattering della luce che c’interessa è quello che emette fotoni in una di queste due direzioni. Tutte le altre possibilità, quando vengono combinate, danno una freccia finale nulla.

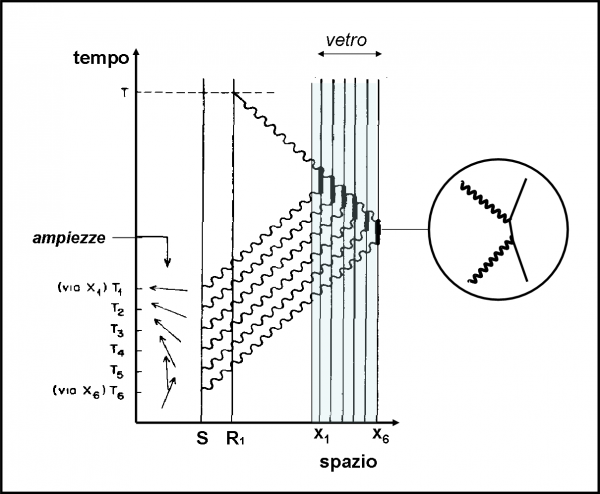
Possiamo perciò semplificare la figura, considerando come ampiezze da sommare alla fine solo quelle che colpiscono i punti mediani relativi a ogni straterello  (da x₁ a x₆).  (Nota Bene: devo ammettere di aver commesso una piccola inesattezza nelle Fig.  63 e 63bis  ( e lo commetterò anche per quella relativa alla trasmissione della luce). Per semplicità di disegno ho sempre fatto avvenire lo scattering nella parte terminale degli straterelli.  In realtà era meglio utilizzare un punto medio, ma… fatico già abbastanza a fare tutte queste figure e spero mi perdoniate… L’importante è saperlo).

Ovviamente, avremmo una precisione maggiore aumentando il numero di strati. Mi raccomando, non fissatevi sull’angolo delle traiettorie incidenti: esso non è assolutamente l’angolo di incidenza, ma rappresenta solo la velocità della luce c costante.  Quello che conta è solo la posizione dei punti all’interno  della lastra di vetro: la figura “spaziale” in due dimensioni è quella di Fig.  63bis e i punti sono situati tutti sulla verticale, linea mediana tra sorgente e rivelatore.

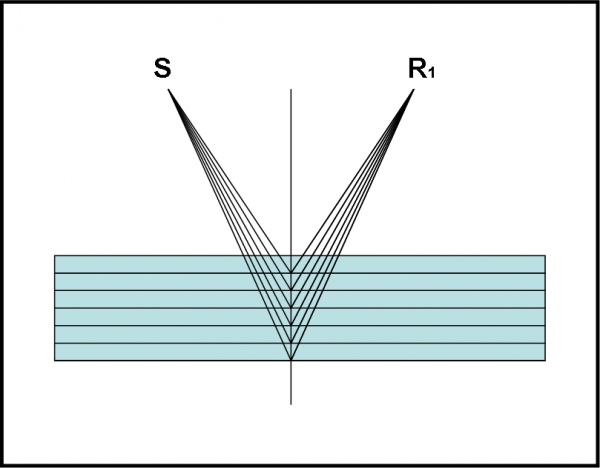
Torniamo alla Fig. 63 e iniziamo a calcolare le ampiezze lungo le traiettorie spazio-temporali che toccano i sei punti considerati. Sono quelle che permettono di finire in R1 nello stesso istante T. Capisco che può sorgere qualche difficoltà, ma cercate di estraniarvi più che potete dalla solita visione a due dimensioni spaziali. Le traiettorie sono solo e soltanto dei diagrammi di Feynman  relativi allo scattering della luce, come mostrato nel cerchio a destra della figura (lo riconoscete?). Le ampiezze delle loro probabilità permettono di calcolare la P(S,R1) di ogni diagramma attraverso la moltiplicazione delle parti in cui vengono divise, tenendo anche conto delle rotazioni relative ai punti di accoppiamento. Avremo una P(S,R1) per ogni traiettoria e alla fine potremo sommarle vettorialmente. In fondo, è sempre lo stesso procedimento che abbiamo già usato numerose volte.

Ogni singolo tragitto (da x₁ a x₆) può essere diviso in quattro “step”:

(1) un fotone è emesso dalla sorgente in un certo istante

(2) il fotone va dalla sorgente a un certo punto x del vetro

(3) nel punto x avviene lo scattering da parte di un elettrone

(4) il nuovo fotone raggiunge il rivelatore

Stiamo parlando di fotoni, ma sappiamo benissimo cosa intendiamo: l'ampiezza di probabilità che un fotone segua quella particolare traiettoria per finire in R1 al tempo T.

I passi (2) e (4) non causano assolutamente niente. La traiettoria si svolge nell’aria e nel vetro, ma l’ampiezza di probabilità non subisce né accorciamenti né rotazioni (a parte l’indebolimento dovuto alla distanza da percorrere, ma in questo caso interessa poco dato che è uguale per tutte le frecce).

Si può, infatti, assumere che tutta la luce segua il percorso tracciato, senza perdite o dispersioni (come indicano, in fondo, i diagrammi “simbolici” di Feynman nei tratti rettilinei).

Il passo (3) è lo scattering vero e proprio e implica accorciamento e rotazione, ma è una costante che dipende dal tipo di materiale, ossia il vetro. L’abbiamo chiamata Sc all’inizio del capitolo. Esso dà sicuramente luogo a un certo accorciamento e a una rotazione in senso orario che per il vetro risulta essere di 90°.

Il passo (1) è invece decisivo, dato che ogni traiettoria inizia a un tempo diverso e, di conseguenza, la freccia è diretta in una direzione variabile con regolarità (luce monocromatica). In poche parole, il passo (1) esegue in un istante quello che il vecchio “cronometro” faceva lungo la traiettoria. Se guardiamo la Fig. 63 vediamo benissimo che la distanza percorsa della luce nelle varie traiettorie è più piccola per x1 e più lunga per x6. Succede proprio quello che avevamo detto poco fa: per arrivare tutti assieme è necessario che chi fa il percorso più corto parta per ultimo e chi fa il percorso più lungo parta per primo.

Moltiplicando le ampiezze dei vari passi, otteniamo, quindi, frecce tutte accorciate della stessa lunghezza e tutte girate di 90° (a causa dello scattering nel vetro). Le differenze tra le loro direzioni rimangono identiche a quelle relative agli istanti in cui hanno lasciato S. Non ci resta che sommarle com’è rappresentato in Fig. 64. A sinistra abbiamo le sei frecce iniziali, come erano disegnate nella Fig. 63. Per non complicare la figura, abbiamo eseguito l’accorciamento e la rotazione (freccetta rossa) solo per la numero 1. Le frecce finali di ogni traiettoria vengono sommate vettorialmente nella parte destra, ottenendo l’ampiezza finale della probabilità che ha un fotone, partito da S, di colpire il rivelatore al tempo T.

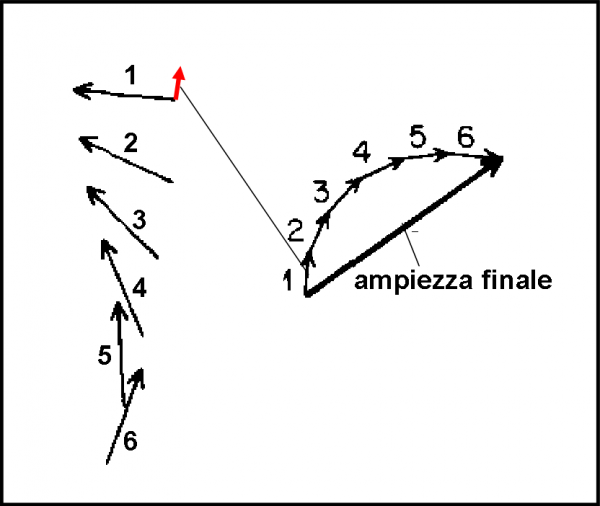
Ancora un piccolo sforzo e finiamo questo “terribile” capitolo. Le frecce seguono un tratto di circonferenza, di cui la freccia finale è la relativa corda. E facile intuire che quando il tratto di circonferenza diventa esattamente la metà della stessa, la corda non è altro che il diametro. Essa è anche il valore massimo dell’ampiezza di probabilità. Poi la corda inizia ad accorciarsi per arrivare a zero quando si chiude la circonferenza. Questa variazione dipende dal tempo tra la prima e l’ultima traiettoria, ossia dallo spessore del vetro.

Un piccolo accenno alla realtà quotidiana: non vi sarà certo sfuggito il perfetto accordo con la “classica” lunghezza d’onda. Il periodo per compiere un intero giro della freccia è proprio la lunghezza d’onda divisa per la velocità della luce. Lo spessore del vetro, che porta a un giro completo della freccia, è proprio la lunghezza d’onda…

Torniamo a noi e vediamo perché avevamo potuto ridurre il tutto a due sole riflessioni (superficie superiore e inferiore), con quello “strano” ribaltamento della freccia per la prima riflessione e non per la seconda. Era solo un semplice “trucco”… Dimostriamolo con la Fig. 65.

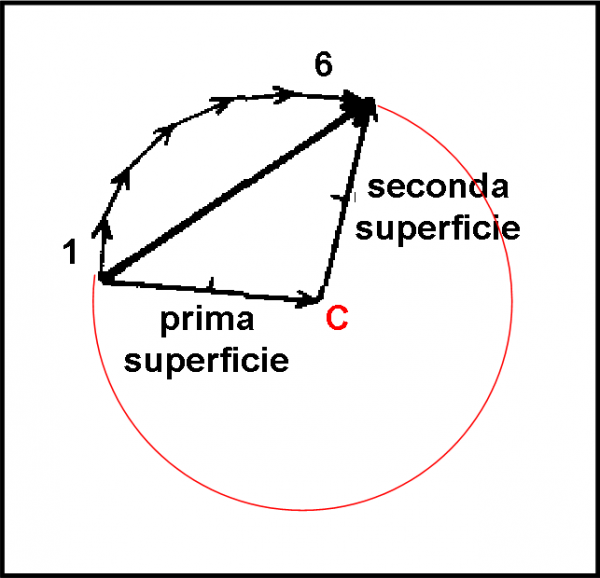
Consideriamo la stessa situazione precedente e individuiamo il centro C della circonferenza descritta dal’ampiezza. Tracciamo i due raggi che contengono la corda. Possiamo dire, con tranquillità, che la somma vettoriale dei due raggi è uguale alla corda, ossia all’ampiezza finale. Tuttavia, per poter sommare questi due raggi, è necessario invertire il verso del raggio che dal centro arriva all’inizio della freccia 1. Quello che va dal centro alla fine della freccia 6 rimane invece immutato. Cosa concludiamo? Per ottenere l’ampiezza finale basta sommare il primo raggio ribaltato e il secondo lasciato inalterato.

Considerando il primo come la freccia della prima riflessione e il secondo come quello della seconda riflessione, il gioco è fatto! Non commettiamo nessun errore, dato che il diametro del cerchio ha un’ampiezza di 0.4 (come si determina attraverso calcoli ed esperimenti). Ogni raggio vale, quindi, 0.2, proprio il numero magico che dava luogo alle ampiezze che variavano da 0 a 0.4 (e alle probabilità finali dallo 0 al 16%).

Nei capitoli iniziali, abbiamo potuto falsificare la situazione assumendo che la riflessione attraverso una lastra di vetro avvenisse solo nella prima e nella seconda superficie, dando luogo a due frecce di ampiezza uguale a 0.2 che si combinavano tra loro. La prima, però, doveva essere ribaltata di 180°.

In realtà, abbiamo visto che tutto si verifica “quantisticamente” attraverso lo scattering della luce in ogni punto della lamina. Possiamo quindi concludere che  la riflessione parziale di una lastra di vetro dipende solo e soltanto dallo scattering della luce all’interno del vetro. Tutto si riduce a una parola semplicissima dell’alfabeto che abbiamo imparato da poco. E la stessa cosa capita per qualsiasi fenomeno legato alla luce e alla sua interazione con la materia.

Appendice (facoltativa) per i più curiosi

Qualche parola in più sul valore 0.4 dell’ampiezza finale. Il raggio della circonferenza dipende essenzialmente dall’ampiezza delle singole freccette che lo descrivono. Quest’ultima dipende dall’ampiezza Sc che ha un elettrone del vetro di produrre un’azione di scattering. Lo scattering, però, non è altro che una parola dell’alfabeto di Alice-Feynman, formata dalle tre uniche sue lettere. Con le formule a disposizione e tenendo conto di tutte le possibili strade che permettono tale azione si può arrivare al valore del raggio della circonferenza. Per sostanze semplici, il calcolo non è impossibile, mentre per sostanze più complesse (come il vetro, ad esempio) sono stati necessari esperimenti di laboratorio. In realtà, il valore di 0.2 approssima molto bene la riflessione che avviene con la luce che colpisce perpendicolarmente la lamina.

Beh… direi proprio che può bastare. Lo ammetto, questa volta è stato un capitolo piuttosto “ostico” (non per niente gli ho affibbiato quattro asterischi). La prossima volta, utilizzando lo stesso sistema “serio” vedremo casa succede alla luce che penetra nel vetro e finisce nel rivelatore al di sotto della lamina. Coloro che sono riusciti ad affrontare questa parte senza grossi problemi, possono anche cercare di descrivere, da soli, il passaggio attraverso la lamina. Questa sarà sempre divisa in sei straterelli, ma sarà ancora necessario considerare traiettorie partite in tempi diversi?

Provateci… è più semplice di quanto non sembri, basandosi sempre sullo scattering, dato che ormai siamo abbastanza “grandi” da scrivere parole compiute nel nuovo alfabeto. Anche se -forse- non li analizzeremo in dettaglio, si può intuire come  i  fenomeni di scattering siano tutti riconducibili a una sola parola del mondo di Alice…

Alla prossima e buon divertimento