Abbiamo visto che vi sono molte strade per giungere al rivelatore R₁, attraverso la doppia riflessione (che sappiamo essere stata una semplificazione indolore), dato che ogni punto della lamina contribuisce alla probabilità finale attraverso l’umile lavoro degli elettroni del vetro, capaci di assorbire e di riemettere fotoni nella direzione che ci interessa. Sono dei veri e propri “fucili mitragliatori” che raccolgono proiettili e li sparano verso il bersaglio.

Zone diverse del vetro, però, vogliono dire percorsi più o meno lunghi e quindi istanti di partenza, dalla sorgente, diversi. Ormai sappiamo che non esiste il famoso cronometro, ma che la direzione dell’ampiezza si origina fin dall’inizio a seconda dell’ora segnata da un unico orologio, al momento della partenza della luce monocromatica. Essa viene ristretta e rivoltata solo quando gli elettroni fanno il loro lavoro, ossia quando applicano la terza lettera dell’alfabeto: l’interazione o accoppiamento.

Un fotone che non … riflette

Pensiamo, adesso, alle traiettorie del nostro fotone che voglia  attraversare tutta la lamina e arrivare in R₂ (perché lo faccia lui e non i suoi fratelli riflessi resta, ovviamente, un mistero). Disegniamo la Fig. 66. Come già fatto precedentemente, consideriamo solo percorsi rettilinei. Il modo migliore per arrivare in R₂ è quello di non incontrare nessun elettrone, ossia non subire scattering. E’ sicuramente la via più diretta e più probabile, dato che non vi sono accorciamenti o rotazioni. La sua ampiezza è decisamente grande, praticamente identica a quella iniziale (a parte l’affievolimento dovuto alla distanza da percorrere, che NON dipende dal vetro). Tuttavia questa stessa traiettoria è irta di ostacoli: gli elettroni del vetro.

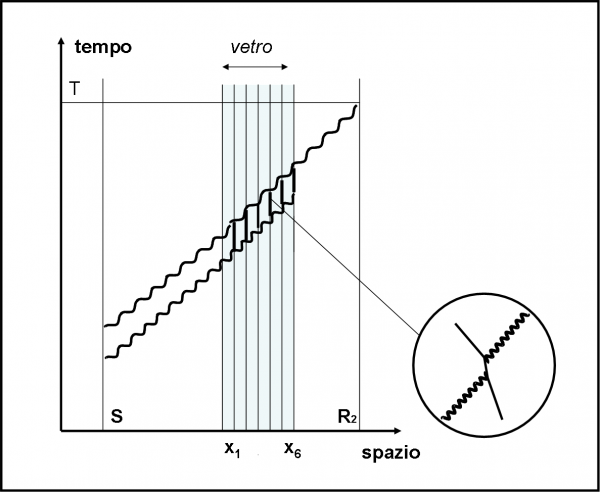
Altri fotoni (o, meglio, altri percorsi alternativi) possono dar luogo a scattering. In prima approssimazione, prendiamo in considerazione le ampiezze che derivano da uno scattering avvenuto all’interno di uno dei sei “straterelli” del vetro. Esse sono decisamente più corte di quella “diretta” e, inoltre, sono ruotate di 90° (come nel caso della riflessione… siamo o non siamo nel vetro?). Tuttavia, ognuna subisce la stessa identica azione e quindi sono tutte uguali tra loro. Cosa dire della loro direzione? Sappiamo che dipende dal momento della partenza dalla sorgente S. Ma, questa volta, tutte le varie alternative da tenere in conto avvengono sullo stesso percorso spazio-temporale, dovendo arrivare tutte in R₂ al tempo T (qualcuna esegue lo scattering prima, altre dopo, ma alla fine il percorso è uguale, ossia attraversa tutta la lamina). La luce deve quindi essere inviata da S nello stesso istante. Quella “diretta” è  teoricamente inviata dopo, ma c’interessa poco, dato che la differenza di direzione è compresa nella rotazione di 90° (come già considerato nella riflessione).

In conclusione, abbiamo una freccia molto lunga (praticamente unitaria) a cui si devono sommare sei freccette uguali, ruotate tutte di 90° e quindi situate lungo la stessa direzione, come rappresentato in Fig. 67.

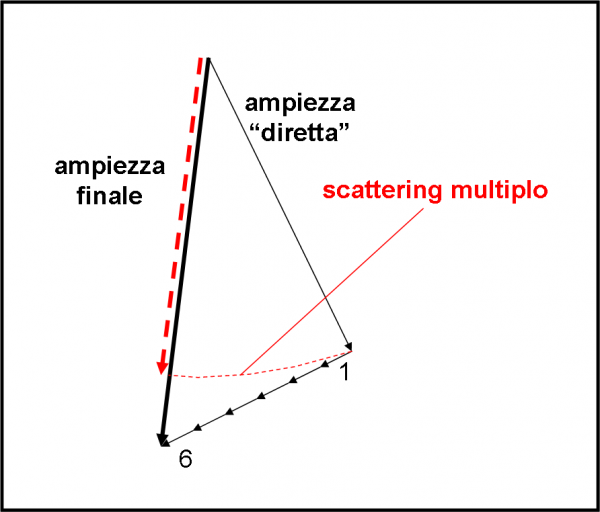
A prima vista sembrerebbe che l’ampiezza finale sia più lunga di quella della via diretta. In realtà non è vero, se si considerano scattering multipli (in pratica, quello che avevamo fatto considerando riflessioni multiple all’interno del vetro). Alla fine si ottiene una freccia finale che è, al massimo, uguale, come lunghezza, a quella della luce diretta. D’altra parte deve essere così se non si vuole concludere che mettere una lamina di vetro davanti alla luce aumenti la probabilità rispetto a un percorso senza alcun ostacolo! Lo scattering multiplo gioca in modo che non si ottenga più luce di quanta se ne invii… e inoltre permette all’ampiezza finale di andare da 0.92 a 1 e, di conseguenza, assecondare la riflessione e ottenere una probabilità finale, data dalla somma “bruta”  dei due eventi separati (riflessione e trasmissione), pari al 100%. La Natura lavora in modo bizzarro, ma non sbaglia un colpo… come la QED ci dimostra!

Il fatto che l’ampiezza finale, dopo la trasmissione attraverso il vetro, ruoti rispetto a quella del passaggio senza scattering (percorso diretto, come se vi fosse solo aria), crea l’impressione che il vetro ritardi il passaggio della luce (ossia la luce impieghi più tempo). In realtà, questo effetto è dovuto alla rotazione e all’accorciamento della freccia a causa dello scattering. Questa capacità di “rallentamento” dovuto alla minore o maggiore inclinazione della freccia finale si chiama indice di rifrazione del materiale. Lo stesso effetto si ottiene, ovviamente, aumentando lo spessore del vetro, dato che si sommano più freccette e la direzione finale si piega di più. Questo è il vero fenomeno su cui si basa una lente, che utilizza uno spessore variabile. In parole semplici, dato che la freccia finale ha una certa inclinazione rispetto a quella senza scattering (ossia quella prima dell'entrata nel vetro) si conclude che essa deve essere partita a un tempo diverso rispetto a quello dell'ampiezza senza scattering. Tempo diverso vuol dire più tempo per raggiungere il rivelatore... e il gioco è fatto: la luce sembra viaggiare più lentamente.

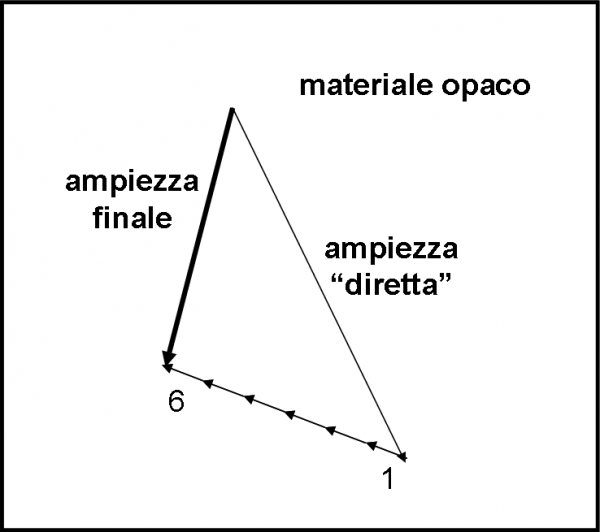
Quanto detto vale per materiali trasparenti. Se il materiale è più “opaco”, la direzione delle freccette da sommare a quella principale fa un angolo minore di 90° e quindi l’ampiezza finale si riduce rispetto a quella diretta. Non solo ruota, ma si accorcia di molto. Questo vuol solo dire che un materiale opaco ha una minore probabilità di essere attraversato dalla luce. Vediamo la situazione in Fig. 68.

Uno più uno uguale a quattro

Sembra impossibile che tutti i fenomeni di interazione tra luce e materia possano essere descritti attraverso tre sole lettere di un alfabeto. Se entrassimo a fondo nella matematica che c’è dietro riusciremmo a verificarlo direttamente. Ma questa impresa va oltre le nostre possibilità. Limitiamoci a pochi altri fenomeni e poi abbandoniamo con un po’ di nostalgia la QED.

Torniamo al ben noto fenomeno dell’interferenza, che ormai conosciamo come le nostre tasche. Affrontiamolo nello spazio-tempo. Consideriamo il caso più generale: due sorgenti S₁ e S₂ e due ricevitori R₁ e R₂. L’evento da verificare è: un fotone parte da S₁ e uno da S₂. Entrambi devono raggiungere R₁ e R₂. Sappiamo che esistono due vie perché l’evento accada. Le traiettorie S₁R₁ e S₂R₂, ma anche la S₁R₂ e la S₂R₁ (Fig. 69) Le ampiezze associate ad esse sono: P(S₁,R₁), P(S₂,R₂), P(S₁,R₂) e P(S₂,R₁). Esse vanno moltiplicate a coppie, dato che solo così si ha l’ampiezza finale per ogni alternativa. Abbiamo le frecce P(S₁,R₁) x P(S₂,R₂) e P(S₁,R₂) x P(S₂,R₁). I due risultati vanno sommati vettorialmente per ottenere l’ampiezza finale. Una vera banalità per noi. Agendo così nasce il fenomeno dell’interferenza, dato che, variando le posizioni relative delle sorgenti e/o dei rivelatori, possiamo avere sia la somma che l’annullamento della luce.

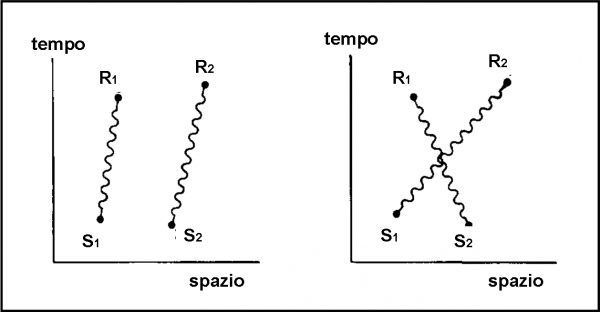
Immaginiamo, ora, che i due rivelatori si sovrappongano. Vale comunque il calcolo di prima che porta, però, a due ampiezze uguali attraverso la moltiplicazione, dato che P(S₂,R₁) = P(S₂,R₂)  e P(S₁,R₁) = P(S₁,R₂). Ossia, P(S₁,R₁) x P(S₂,R₁) = P(S₂,R₁) x P(S₁,R₁). Ne consegue un’ovvia … ovvietà: in R₁= R₂ = R,  entrambe le vie danno la stessa ampiezza (freccia) da sommare.  Lunghezza e direzione sono identiche per costruzione! La somma delle due frecce è uguale a 2 volte l’ampiezza singola e, quindi, dato che la probabilità finale  è il quadrato dell’ampiezza finale, essa è pari a quattro volte quella della singola moltiplicazione. La faccenda è rappresentata in Fig. 70.

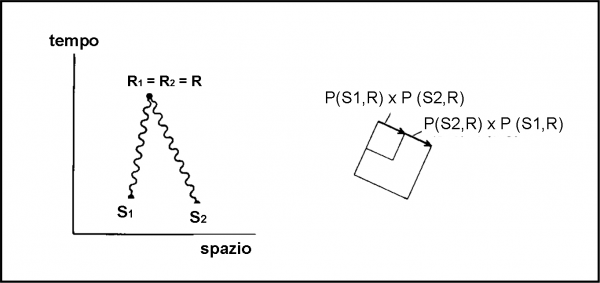
Abbiamo detto qualcosa di interessante? A prima vista sembrerebbe di no. Ma, pensiamoci, un po’ sopra… Se spostassimo le due sorgenti, cosa succederebbe? Una cosa del tutto identica: si otterrebbe, in R, sempre la somma di due frecce identiche e una probabilità quattro volte quella della singola moltiplicazione. L’interferenza non fluttuerebbe più, ma sarebbe sempre positiva. Per farla diventare zero dovrebbe essere nulla la singola freccia, che, però, non lo è sicuramente.

Se aumentassimo il numero di fotoni che escono dalle sorgenti, l’effetto sarebbe sempre più macroscopico. In altre parole, questo risultato vuol dire che i fotoni tendono verso una stessa “condizione” (il rivelatore è una condizione) o -meglio- “stato”. Non possiamo approfondire di più, ma i risultati pratici sono enormi. La probabilità che un atomo emetta un fotone aumenta di molto se alcuni fotoni sono già presenti. Questo fenomeno è stato studiato da Einstein e prende il nome di emissione stimolata. I laser lavorano proprio basandosi su di lei.

O uno o l’altro

Se facessimo la stessa cosa con gli elettroni dovremmo trovare lo stesso risultato. Invece capita proprio il contrario, dato che bisogna tener conto che essi sono polarizzati (finora non avevamo avuto bisogno di inserire questa caratteristica fondamentale). Si può dire che il loro spin NON può essere zero (ma questa è un’altra storia). In ogni modo, ciò che capita è che le due frecce ottenute dalle due moltiplicazioni, hanno uguale ampiezza e verso opposto (Fig. 71). Ciò vuol dire che l’ampiezza finale è sempre ZERO. In parole povere, gli elettroni, a differenza dei fotoni, non amano andare nello stesso luogo! E questo, in fondo, lo sappiamo bene…

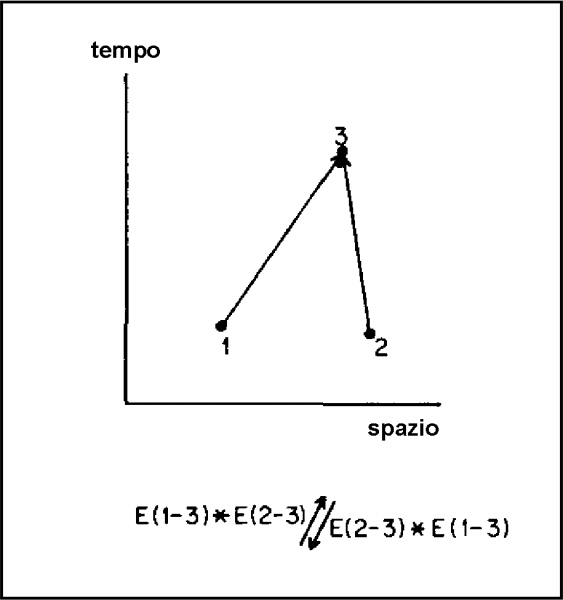
Più tecnicamente, si conclude che due elettroni con lo stesso spin non possono trovarsi ambedue nella stessa posizione. Questo risultato prende il nome di principio di esclusione. Penso che questo nome non suoni tanto astruso … Da questo principio seguono moltissime delle proprietà chimiche dell’atomo. Tutto si basa solo e soltanto sullo scambio di fotoni tra protoni ed elettroni e sulla loro impossibilità di convivere con i fratelli. Se gli elettroni non fossero polarizzati si ammucchierebbero tutti attorno al loro nucleo atomico e non potrebbero essere catturati facilmente da altri atomi. Insomma: le reazioni chimiche sarebbero molto, molto difficili! Un giorno, magari, ne parleremo.

Un inseguimento perfetto

Senza entrare nei particolari tecnici, facciamo un esempio di come la QED abbia aiutato nel calcolare teoricamente un “numero” estremamente importante nel contesto della fisica delle particelle elementari. Il grande Dirac riuscì a calcolare il momento magnetico di un elettrone, ossia la risposta dell’elettrone a un campo magnetico esterno. Il valore venne determinato attraverso i calcoli e risultò essere uguale semplicemente a 1, in certe unità di misura. In seguito si ci accorse, attraverso gli esperimenti, che quel valore non era esatto ed era pari a circa 1.00118. Cercando di miglioralo attraverso considerazioni teoriche la faccenda degenerò, dato che il numero tendeva a infinito, ossia a un’assurdità. Una prima e rozza applicazione della QED ottenne, invece, 1.00116, ben più vicino al valore sperimentale. La strada era quella giusta.

Negli anni ’80 del ventesimo secolo, la QED ottenne un valore di 1.00115965246 (con un errore di 5 unità nell’ultimo decimale) contro un valore sperimentale di 1.00115965221 (con un’incertezza di 4 unità nell’ultima cifra). Un risultato niente male, se pensiamo che stiamo parlando di incertezze equivalenti allo spessore di un capello di una persona di New York, visto da Los Angeles.

Come si è arrivati a questo risultato eccezionale? Facile (si fa per dire): aggiungendo più lettere alla “parola” base dell’interazione elettrone-fotone. Il valore 1 ottenuto da Dirac, si riferisce, infatti, alla traiettoria più semplice, ossia a quella di un elettrone che assorbe un fotone generato dal campo magnetico (Fig. 72).

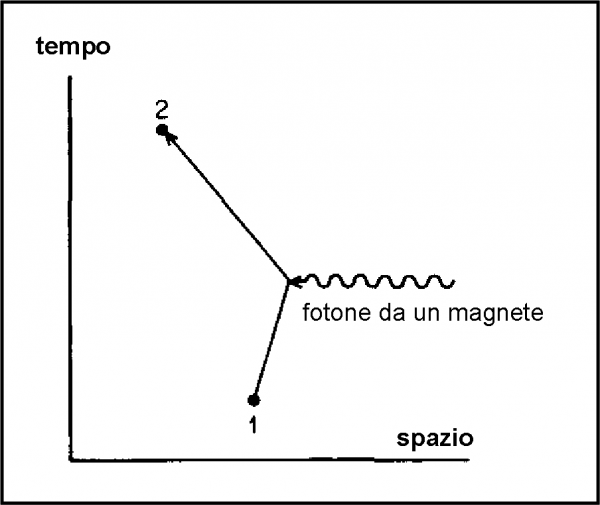
Complicando leggermente il percorso (ossia introducendo un’altra interazione) si arriva al valore di 0.00116. Qual è questo percorso alternativo? Lo vediamo in Fig. 73. E’ capitata una cosa “assurda”, ma non certo per il mondo di Alice: un fotone virtuale è stato emesso ed è stato riassorbito dallo stesso elettrone. Un gesto di cannibalismo? No, cari amici, le formule della QED lo ammettono e non dobbiamo farci condizionare dal nostro … moralismo.

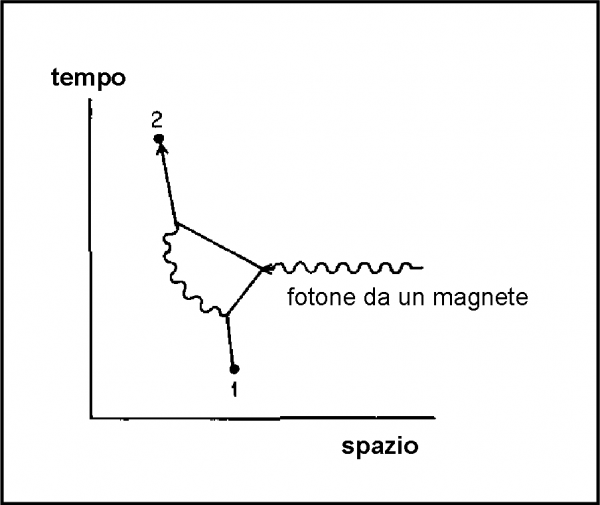
Intanto, però, gli esperimenti miglioravano il numero, aggiungendo nuovi decimali. Problemi? No di certo per la QED. Bastava aggiungere altri percorsi alternativi come quelli raffigurati in Fig. 74. Nessuna sorpresa, ammettendo perfino, ultimo grafico a destra, che un elettrone e un positrone si creino da un fotone e si distruggano per emettere un nuovo fotone (cerchietto che si chiude su se stesso).

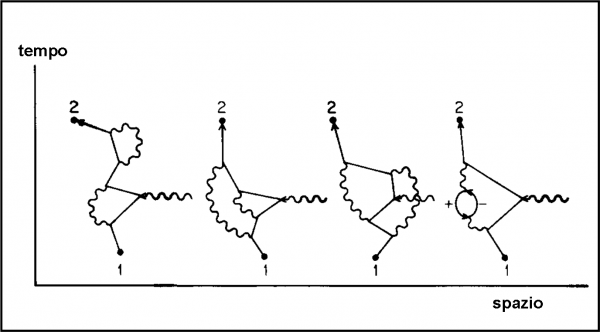
Il valore sperimentale migliorava ancora? E, allora, via con qualche ulteriore “accoppiamento”, come mostrato nella Fig. 75, che rappresenta solo tre di una serie di 70 “combinazioni”: il valore teorico rimane incollato a quello sperimentale. Fantastico. Malgrado la Natura tenti di essere sempre più imprevedibile, la QED non si fa impressionare.

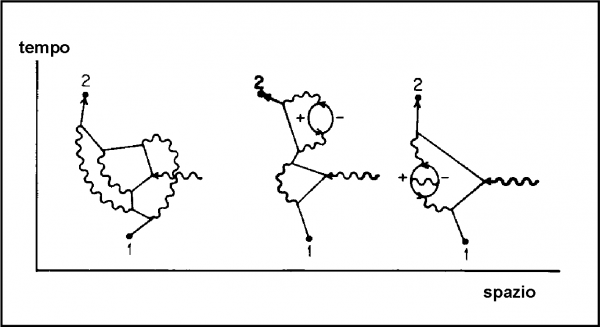
Non crediamo, però, che sia stato facile aumentare gli accoppiamenti e calcolare la quantità da aggiungere, proveniente da un numero sempre crescente di percorsi alternativi. Ogni miglioramento ha necessitato di periodi di tempo molto lunghi, che l’avvento dei supercomputer ha decisamente sveltito, fino a portare alla precisione odierna… (se non sbaglio, dovremmo essere a 1.01159652188 sperimentale contro 1.01159652140 teorico). Sembra un bel piccolo miglioramento, ma più si va nel piccolo e più le combinazioni aumentano e di conseguenza i calcoli relativi… In qualche modo si è spaccato un capello in dieci!

Conclusioni

C’è poco da dire. La QED sembra uniformare tutti i fenomeni della fisica (funziona anche con altre particelle e non solo con i fotoni e gli elettroni). Quello che stupisce è la semplicità dell’alfabeto e la continua ripetizione di azioni sempre uguali tra loro: moltiplicazioni e somme di ampiezze. Eppure tutto (o quasi) torna benissimo. Feynman non  è stato l’inventore della QED, ma, a parte il contributo fondamentale che gli è valso il Nobel, solo lui è riuscito a renderla simile a una semplice e fantastica avventura. Non ci resta che applaudirlo!!!

Una bella fatica, ma penso ne sia valsa la pena…