Per una trattazione completa, inserita in un contesto più ampio, dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Un corpo nero è un corpo che non esiste in Natura e che non è nemmeno nero. E’ un qualcosa di ideale che, però, si riesce a costruire abbastanza bene in laboratorio. Possiamo considerarlo come un corpo che assorbe tutta la luce che riceve senza rifletterla (da qui il nome di “nero”). Tuttavia, l’energia deve conversarsi e, di conseguenza, il corpo deve in qualche modo riemettere l’energia che ha assorbito.

Tu dai una cosa a me e io do una cosa a te

Come può avvenire questo processo? Bene, in modo molto semplice: l’energia elettromagnetica assorbita aumenta la temperatura del corpo che acquista energia termica, ossia mette in agitazione le particelle microscopiche. Agitazione vuole dire energia cinetica che dà luogo a energia elettromagnetica che abbandona il corpo. Questo processo si chiama irraggiamento e non è altro che l’emissione di onde elettromagnetiche (i fotoni, insomma), generate dall’agitazione delle particelle a causa della temperatura raggiunta. Molto simile a ciò che avviene all’interno delle stelle…

A seconda della temperatura, varia la frequenza delle onde elettromagnetiche, ossia la loro energia. Ad esempio, a temperatura ambiente vengono emesse onde infrarosse (ed è per questo che gli occhiali infrarossi permettono di vedere gli esseri viventi anche di notte); oggetti molto freddi emettono onde radio; oggetti molto caldi onde ultraviolette fino ai raggi X e gamma. Questi esempi ci ricordano un fatto che a volte crea qualche confusione. La temperatura di un corpo si alza attraverso l’assorbimento di energia elettromagnetica (come quella che arriva dal Sole) e, dopo l’assorbimento, il corpo riemette energia elettromagnetica. Che differenza c’è tra le due? Presto detto: la frequenza delle onde.

Prendiamo come esempio proprio il corpo nero. Se è nero vuol dire che non emette nel visibile se no lo vedremmo colorato. Però, riceve luce visibile per scaldarsi. In altre parole, riceve onde con la frequenza del visibile e riemette nell’infrarosso, invisibile ai nostri occhi. Ne segue che il corpo nero può benissimo non essere nero. Lo è soltanto a temperatura ambiente. Se alziamo la sua temperatura inizia a colorarsi perché emette nel visibile e passa dal rosso, al giallo al blu. Poi, nell’ultravioletto, ricominciamo a non vedere più niente, ma il corpo continua a emettere (e come!) anche a lunghezze d’onda sempre più corte (frequenza maggiore).

Un piccolo inciso che verrà utile tra non molto. Le stelle hanno una temperatura tale da inviare la luce soprattutto in certe lunghezze d’onda che i nostri occhi riescono a vedere. In altre parole, il massimo della radiazione avviene quasi sempre nella stretta zona dello spettro elettromagnetico che noi chiamiamo visibile (dal rosso al violetto). Basterebbe che fossero molto più fredde o molto più calde e non riusciremmo a vederle. Oggi sappiamo che esistono corpi celesti che emettono in una zona vietata ai nostri occhi, ma ormai abbiamo costruito gli occhiali necessari allo scopo. Tuttavia, le abbiamo scoperte solo perché hanno la giusta temperatura. Insomma, hanno fatto di tutto per essere viste. Ah… questi fotoni! hanno proprio saputo che frequenza scegliere.  Non possiamo che ringraziarli… se no saremmo vissuti senza stelle e senza astronomia… Un attimo, però. Quasi sicuramente il discorso va visto al contrario. Le stelle emettono dove gli pare e piace, ma sono stati i nostri occhi a essere predisposti per “leggere” proprio quel tipo di lunghezza d’onda. Beh… forse sì, dato che le stelle sono nate prima di noi. Torniamo al nostro corpo nero che emette dove vuole.

In realtà, il corpo emette in tutte le lunghezze d’onda, ma ne “preferisce”  qualcuna, legata alla temperatura che ha raggiunto. Bene, è ora di spiegarci meglio e di introdurre un corpo nero sperimentale quasi perfetto.

Costruiamone uno abbastanza “ideale”. Come ci mostra la Fig. 1, basta utilizzare una larga cavità completamente isolata dall’esterno con un foro piccolissimo che permetta di fargli entrare l’energia. I fotoni che entrano cominciano a sbattere contro le pareti, si riflettono e un po’ alla volta vengono “assorbiti”. La loro energia si trasferisce  in energia cinetica, ossia in calore. Di sicuro non possono più uscire se il foro è abbastanza piccolo. Sarebbe come trovare un ago in un pagliaio. Continuiamo a inviare energia fino a raggiungere una temperatura costante all’interno della cavità.  Siamo in condizioni di equilibrio termico.

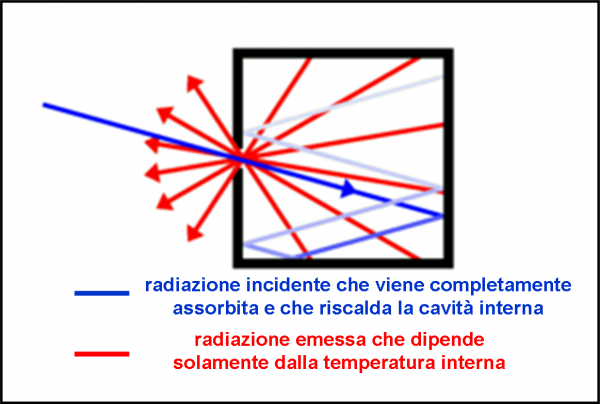
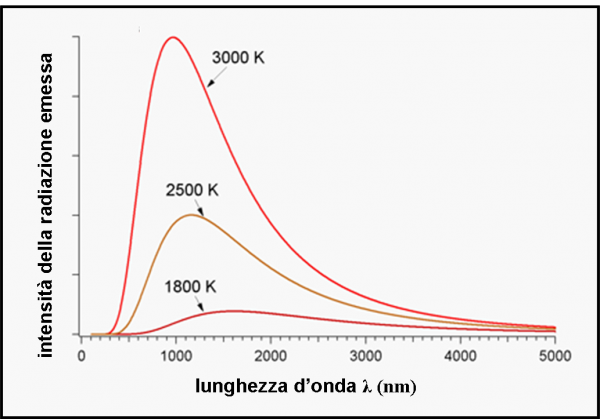
Il foro diventa, adesso, anche lo spioncino per studiare l’energia che viene emessa. Infatti, l'energia cinetica (calore) causa urti e libera fotoni, ossia energia elettromagnetica. Basta farla passare attraverso un prisma (ma c’è di meglio) e vedremmo che questa radiazione si distribuisce in funzione della lunghezza d’onda λ (o della frequenza ν, che non è altro che ν = c/λ, dove c è la velocità della luce). In altre parole, si può misurare quanta energia viene emessa per piccoli intervalli di lunghezza d’onda o di frequenza (come preferiamo). Si ottiene uno spettro della luce, o -meglio- uno spettro elettromagnetico come quello che ci mostra la Fig. 2, che riporta l’energia emessa in funzione della lunghezza d’onda per tre diverse temperature. Ci torneremo presto…

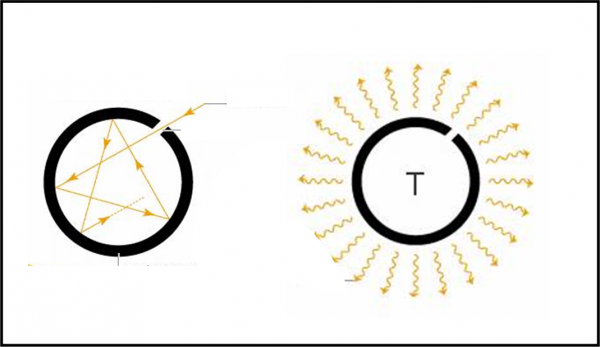
Un chiarimento per non creare confusione. A volte, si vedono disegni che illustrano il corpo nero e il suo irraggiamento come quello di Fig. 3. In questo caso si simula visivamente ancora meglio una stella, dato che il riscaldamento avviene all’interno della sfera cava, mentre sono poi le pareti esterne a emettere la radiazione. Ciò vuol dire che, in questo caso le pareti esterne non sono isolate. Tuttavia, la soluzione presentata precedentemente ha il vantaggio di avere un punto d’uscita ben determinato del flusso luminoso ed è quindi più facile da analizzare. Comunque, il “succo” dell’esperimento è esattamente lo stesso.

La tremarella che non si vede

Descriviamo ancora meglio l’irraggiamento termico. Ripetere non fa mai male. Per fare stare veramente fermo un corpo dovremmo essere alla temperatura di 0 K, ossia allo zero assoluto (-273 °C). In questo caso, tutte le particelle più piccole si possono considerare ferme. Consideriamo un atomo con i suoi elettroni piazzati attorno a lui in una quiete perfetta. Cominciamo ad aumentare la temperatura. Gli atomi iniziano a muoversi, a vibrare (da fuori non possiamo certo vedere questa vibrazione… la sentiremmo solo attraverso la temperatura). Un  atomo comincia a urtare un altro atomo. Gli elettroni sono poco pesanti e sono i primi a essere coinvolti nello scontro. Sono loro ad assorbire l’energia cinetica che gli è stata trasferita nell’urto. Qualcuno salterà rimanendo all’interno dell’atomo e poi tornerà al suo stato iniziale riconsegnando l’energia ricevuta attraverso l’emissione di energia elettromagnetica, ossia emettendo un fotone. Il fotone si muove e sicuramente urta un altro atomo e gli trasferisce la sua energia cinetica. Il gioco continua e nascono fotoni di tutte le energie, ossia di tutte le frequenze. In altre parole, ognuno può essere visto come una vibrazione del campo elettromagnetico di lunghezza d’onda diversa.

Più la temperatura sale e più questo continuo movimento fatto di urti, di elettroni che saltano o addirittura se ne vanno prima di essere magari catturati da un altro atomo, produce sempre più fotoni di tutte le lunghezze d’onda e quindi aumenta la radiazione luminosa, ossia la radiazione termica (dato che è causata dall’aumento della temperatura).

Ormai gli elettroni sono tutti coinvolti nella frenetica danza fatta di spinte sempre più violente. In conclusione, più aumenta la temperatura e più aumenta sia l’energia totale che il corpo emette, sia l’energia che ogni fotone può raggiungere (legata, come già detto) alla frequenza dell’oscillazione.

Tutta questa bellissima e invisibile battaglia tra particelle è ciò che il corpo nero può mostrarci attraverso la misura della radiazione termica emessa e della sua distribuzione. L’unico parametro che causa questo risultato è la temperatura a cui è stato riscaldato. Il discorso non è così semplice, perché le varie lunghezze d’onda dell’emissione dipendono da cosa si scontra: molecole, atomi o solo elettroni. In ogni modo i risultati relativi all’emissione termica di un corpo nero sono indipendenti dal tipo di materiale e dalla forma del corpo che emette. Chi comanda è solo la temperatura e, quindi, anche l’agitazione delle particelle, senza curarsi della loro carta d’identità chimica.

Per la campana e il suo "picco" conta solo la temperatura

Anche se in modo abbastanza empirico, è stato possibile, già nella seconda metà dell’ottocento, descrivere, con due semplici formule, la dipendenza della luce emessa da un corpo nero in funzione della temperatura raggiunta. In particolare, si è stabilito che l’energia  totale della luce emessa per unità di tempo (ossia la potenza) è proporzionale alla quarta potenza della temperatura. In parole matematiche:

E = σ T⁴

dove σ è una costante. Più esattamente, si ricava che il numero di fotoni emessi nel’unità di tempo va con il cubo della temperatura, mentre la loro energia media dipende linearmente da essa. Moltiplicando numero di fotoni per la loro singola energia media otteniamo la quarta potenza enunciata prima. Questa legge prende il nome di legge di Stefan-Boltzmann e lo stesso nome viene dato anche alla costante σ.

Questa legge, importantissima, ci dice quanta energia si produce globalmente al variare della temperatura. Più la temperatura cresce e più energia si produce. Risultato abbastanza comprensibile e logico.

Fatta questa preliminare precisazione, possiamo ricavare un’altra legge empirica molto importante, ricordando che la capacità di oscillare di un fotone è legato alla sua energia. Tanto più è energetico è tanto più corto è il suo periodo di vibrazione e quindi anche la sua lunghezza d’onda. In semplici parole: energia e lunghezza d’onda di un fotone sono inversamente proporzionali. Tuttavia, abbiamo appena detto che l’energia di un fotone dipende in modo lineare dalla temperatura. Ne segue una relazione fondamentale per il corpo nero: tanto più grande è la temperatura tanto più piccola è la lunghezza d’onda. Questa relazione, chiamata legge di Wien, vale, in particolare, per la lunghezza d’onda in cui è massima l’emissione.  Questa legge ci dice che per ogni temperatura si ha un certo valore della massima radiazione luminosa. Sappiamo, però, che ad ogni lunghezza d’onda è associato un certo colore. Ne segue che a ogni temperatura è associato un ben determinato colore in cui si ha il massimo di emissione. La formula di Wien si scrive:

λ_max = k/T

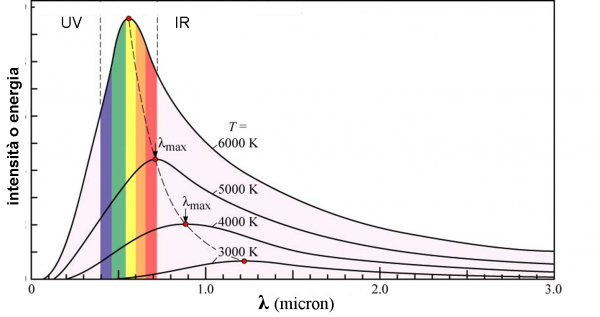
dove k è una costante. Parlando di massimo d’emissione in funzione della lunghezza d’onda non possiamo fare a meno di parlare, in modo più approfondito, dello spettro elettromagnetico del corpo nero, per una certa temperatura, mostrato in  Fig. 2. Esso, come già detto, non è altro che la distribuzione dell’intensità della luce emessa da un corpo nero in funzione della lunghezza d’onda. Proprio quella che si riesce a costruire analizzando la luce che esce dal famoso forellino. Gli esperimenti mostrano molto bene che essa segue una specie di campana, raggiungendo un valore massimo per una certa lunghezza d’onda. Variando la temperatura varia anche lo spettro, seguendo le due leggi appena formulate. Tuttavia, c’è qualcosa che non va…

Ricapitoliamo brevemente: la legge di Stefan-Boltzmann dice che l’energia totale (quella dell’intera campana) è funzione della temperatura, mentre quella di Wien ci dice che il massimo di questa “campana” si sposta verso lunghezze d’onda maggiori per temperature decrescenti. Mettendole assieme, si può dire che la campana sposta il suo massimo verso lunghezze d’onda maggiori, per temperature decrescenti, e che la campana, nella sua totalità, si abbassa. Fin qui tutto bene, come mostra la Fig. 2.

Magnifico. Due leggi molto interessanti e molto utili per il nostro scopo, dato che legano molto bene temperatura, lunghezza d’onda ed energia luminosa. Tuttavia, sarebbe molto bello saper descrivere matematicamente la “campana”, osservata direttamente negli esperimenti. In altre parole, cercare di andare oltre alla legge di Stefan-Boltzmann, e calcolare teoricamente non solo l’energia totale, ma quella relativa a ogni singola lunghezza d’onda.

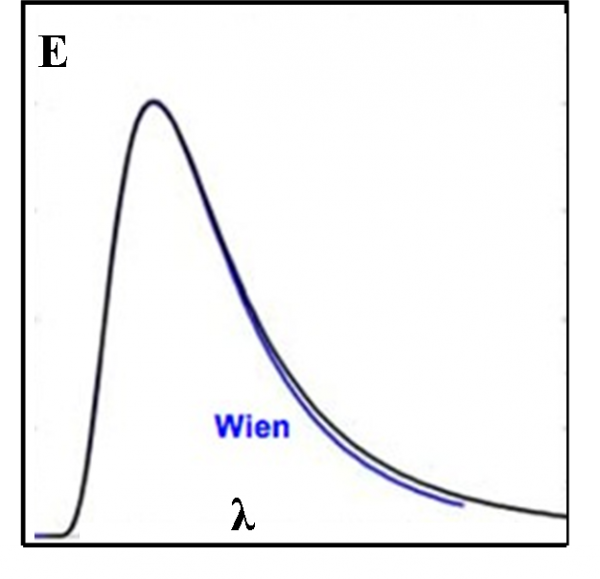
Trafficando con le varie grandezze in gioco, Wien sembrava aver trovato una buona rappresentazione (Fig. 4). Purtroppo, però, andava bene per piccole lunghezze d’onda, ma falliva per grandi lunghezze d’onda. In qualche modo lui aveva lavorato su un gas composto da molecole, dato che ancora non si conoscevano le interazioni tra le particelle più piccole.

Una catastrofe infinita

Utilizzando la teoria elettromagnetica sviluppata da poco, si giunse anche a una legge teorica che stabiliva come l’energia della singola lunghezza d’onda dovesse essere direttamente proporzionale alla temperatura, ma inversamente proporzionale alla quarta potenza della lunghezza d’onda.Essa si chiama legge di Rayleigh-Jeans. Come già detto, essa è una legge teorica, basata sulle nuove teorie dell’elettromagnetismo e dovrebbe funzionare, a meno di non ammettere che le teorie così apparentemente perfette siano, invece, ben lontane dalla verità. Riportiamo questa formula teorica che, però,  non … funziona assolutamente:

ΔE = C T/λ⁴

Dove ΔE è l’energia relativa a un piccolo intervallo di lunghezza d’onda e C una delle “solite” costanti (da non confondere con c che è la velocità della luce!).

Essa va benissimo per lunghezze d’onda molto lunghe, ma per lunghezze d’onda sempre più corte (alte frequenze) porta a valori sempre più alti dell’energia. Teoricamente, per una lunghezza d’onda uguale a zero l’energia diventa infinita. E questo non si vede assolutamente negli esperimenti e nemmeno è un risultato ammissibile. La Fig. 5 ci mostra l’andamento che ci si aspetterebbe dalla legge teorica, confrontato con l’andamento reale di un corpo nero: una vera CATASTROFE per l’elettromagnetismo!

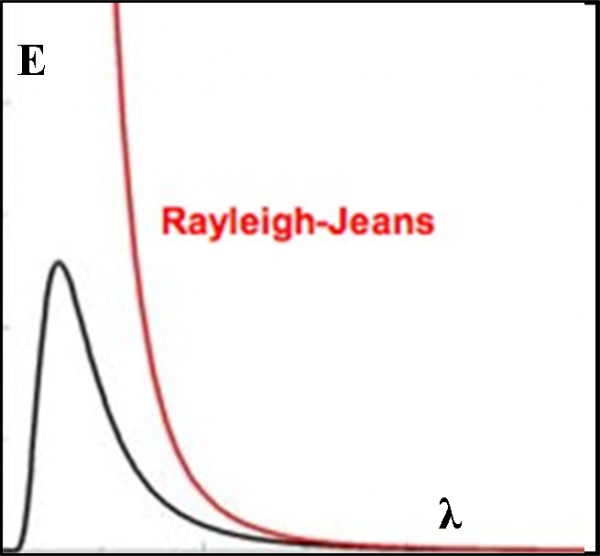
Dato che la parte, subito dopo la minore lunghezza d’onda dello spettro visibile, prende il nome di ultravioletto, questo risultato assurdo venne chiamata proprio catastrofe ultravioletta. Il corpo nero era un meravigliosa astrazione che permetteva di legare perfettamente l’energia dei fotoni (e quindi la luminosità) alla temperatura, ma la legge che doveva descrivere questa relazione sembrava portare a una vera “catastrofe” per le piccole lunghezze d’onda.

Tra poco, affronteremo di petto questa problematica che aprirà le porte, quasi senza volerlo, alla meccanica quantistica e al modello atomico di Bohr. Prima di partire in quarta, ragioniamo un attimo su quello che abbiamo ottenuto con il corpo nero e con la sua distribuzione in funzione della lunghezza d’onda, ossia lo spettro. Anche se non riusciamo a spiegarlo con la Fisica Classica, resta pur sempre un risultato fantastico, soprattutto se accompagnato dalle due leggi di Stefan-Boltzmann e di Wien. Vale la pena riproporre in Fig. 6, qualche spettro elettromagnetico di corpo nero, inserendo le lunghezze d’onda del visibile (ossia i colori dell’arcobaleno o del prisma di Newton). A sinistra del visibile abbiamo l’ultravioletto (UV) e a destra l’infrarosso (IR).

In realtà, lo spettro elettromagnetico è estremamente ampio e la parte visibile è una regione estremamente limitata, come vediamo nella Fig. 7.

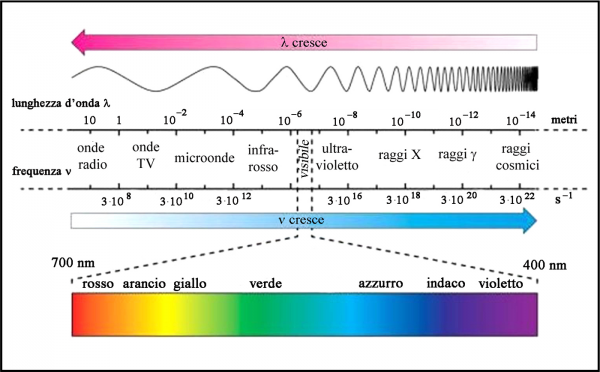
Uno spettro senza regole

Come si vede molto bene dalla Fig. 6, il corpo nero emette secondo uno spettro che sembra descritto da una linea continua. Proprio per questa caratteristica viene chiamato spettro continuo. Uno potrebbe chiedersi perché un corpo caldo emette in questo modo. La risposta sta nel fatto che l’emissione deriva dall’agitazione di un numero incredibile di particelle che modificano in ogni modo la loro energia e, quindi, i fotoni che alla fine lasciano il corpo nero possono assumere qualsiasi lunghezza d’onda, ossia energia. Un mix straordinario che non dipende assolutamente dalla composizione del materiale, ma solo dalla temperatura.

Ovviamente, l’emissione avviene in tutte le lunghezze d’onda, ma non con la stessa intensità. Vedremo tra poco che ciò è legato alla probabilità che si possa fare un salto più o meno energetico. Ad esempio, in certe regioni giocano molto i movimenti molecolari, mentre in altre vengono coinvolti gli elettroni più vicini al nucleo atomico. Insomma, un mix di azioni e reazioni che coinvolgono tutta la struttura delle particelle che compongono la materia. Ovviamente, sotto il controllo unico e generale della temperatura.

Possiamo anche sintetizzare, un po’ rozzamente, la situazione in questo modo: lo spettro continuo dipende dall’interazione tra le particelle agitate dalla temperatura, che avviene in tutti i modi possibili e che, come conseguenza, ripartisce l’energia in gioco senza apparente soluzione di continuità. Esso è prodotto da innumerevoli salti di elettroni liberi, che cioè si muovono tra un nucleo e l'altro. Poiché gli elettroni liberi possono avere energie molto differenti si ottengono fotoni di tutte le lunghezze d'onda (anche se in numero minore o maggiore), che descrivono proprio il "continuo".

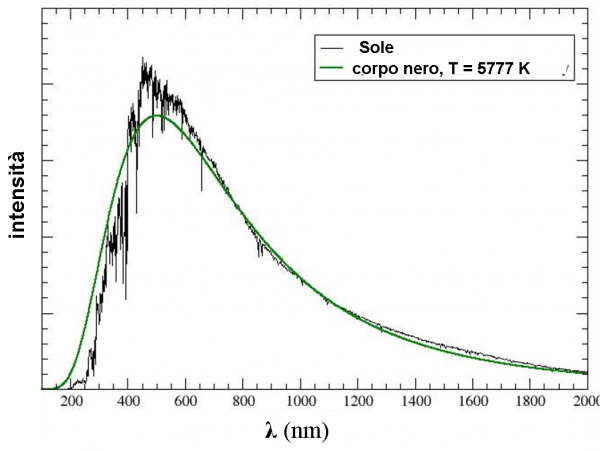
Se, invece, abbiamo a che fare con particelle abbastanza  isolate e  dello stesso tipo, non tutte le energie, e quindi lunghezze d’onda, sono possibili. Esse assorbono energia dai fotoni che le eccitano spostando gli elettroni in modi prestabiliti, e poi la riemettono solo e soltanto secondo regole analoghe, ossia attraverso fotoni con ben determinate lunghezze d’onda. Tutto ciò sempre in base alla temperatura raggiunta, ovviamente. In qualche modo, ogni elemento ha una sua carta d’identità ben precisa. Anzi, come vedremo, ha molte caratteristiche peculiari, delle vere e proprie impronte digitali, le righe spettrali. Un vero spettro stellare è come quello descritto nella Fig. 8, in cui abbiamo considerato proprio il Sole, confrontato con la migliore curva di corpo nero che lo approssima. Quelle righe sono proprio fastidiose e sembrano “sporcare” il nostro spettro. E, invece, sono proprio loro a farci capire come agiscono le stelle e di cosa sono fatte. Ma, andiamo con calma… questa parte la vedremo molto meglio in seguito.

Quale temperatura?

Per adesso, abbiamo già compreso che se il corpo nero potesse essere applicato alle stelle ci permetterebbe di calcolare la temperatura dell’astro, soltanto dalla distribuzione della sua energia o della sua luminosità. Sappiamo, infatti, che ad ogni temperatura corrisponde una ben determinata curva a campana con un certo valore del picco più alto. Sì, ma quale temperatura della stella?

Beh… non certo quella della sua parte più interna, dove l’energia in gioco è spaventosa e dove avviene la vera battaglia tra gravità, energia cinetica e energia nucleare. Tuttavia, ciò che conta è che i fotoni, che partono da quella zona così “calda”, tentino di raggiungere la superficie. Non è facile, come abbiamo già detto, e lo ottengono a passi successivi, aiutati dai fratelli. Ognuno di loro cede la propria energia a qualche elettrone che poi riemette un altro fotone e via dicendo fino a giungere in superficie. Ciò che noi riceviamo, perciò, è relativo alla temperatura della superficie, dato che è lì che si creano i fotoni che raggiungeranno i nostri telescopi.

Lo stesso, in fondo, capita nel corpo nero. Anzi, abbiamo visto che esso può essere sottilissimo, dato che ciò che comanda l’emissione è la temperatura della parte più esterna. Le condizioni sono analoghe. Non basta, però. Il corpo nero ha la caratteristica di assorbire tutta l’energia che proviene dall’esterno e riemetterla  solo in base alla temperatura. La stella è qualcosa di molto simile: non riflette assolutamente niente ed emette solo ciò che le è comandato dall’agitazione delle particelle, atomi o elettroni che siano; ossia, proprio dalla temperatura.

In entrambi i casi l’energia rilasciata dipende solo dalla temperatura dello strato più superficiale.

OK, allora! La prima enorme conquista è stata ottenuta! Analizzando la distribuzione della luce alle varie lunghezze d’onda è possibile, confrontando lo spettro della stella con quello del corpo nero che più gli assomiglia, RICAVARE la temperatura del corpo nero e quindi della stella. Proprio ciò che abbiamo mostrato nella Fig. 8. Fantastico!

La temperatura ha dato il via ai fotoni che non solo ci portano l’informazione luminosa, ma, una volta decodificata, anche la temperatura che li ha aiutati a iniziare il loro viaggio verso di noi. Abbiamo già due grandezze fondamentali: la luminosità (quella che fa splendere le stelle) e la temperatura della loro superficie (senza aver avuto bisogno di un termometro cosmico…).

Due grandezze che possono già permetterci di inserire le stelle in un grafico, avendo due coordinate: luminosità e temperatura. Beh… lo conoscete tutti molto bene: stiamo già abbozzando il celeberrimo diagramma di Hertzsprung Russell.