Categorie: Cosmologia Spazio-Tempo
Tags: cono di luce distanza di Hubble distanze comoventi espansione Universo redshift Spazio-Tempo
Scritto da: Vincenzo Zappalà
Commenti:22
Un riassunto grafico per i più bravi *****
Una figura per i più abili… Un semplice (?) sommario di tutto ciò che vorreste sapere sullo Spazio-Tempo. In pratica riunisce quanto ho scritto, separatamente, in tanti articoli passati. Ovviamente, abbisogna di un po’ di fatica mentale, ma poi aprirà una finestra molto chiara sull’Infinito Teatro del Cosmo…
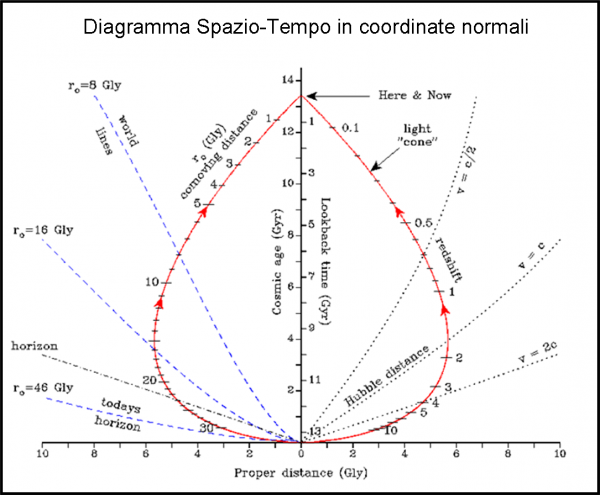
Per chi ha voglia di avere un quadro generale dello Spazio-Tempo, inserisco una figura riferita alle coordinate “normali” (distanze normali e tempo normale). Al suo interno trovano posto tutte le linee e i dati fondamentali (cono di luce, linee di Universo, sfera di Hubble, Universo Osservabile e distanze comoventi, redshift,…). Un riassunto perfetto di quanto abbiamo discusso in tanti articoli passati. Magari, un giorno, riuniremo tutto e la figura sarà un riassunto finale. In qualsiasi caso, però, non chiedetemi di ricavare le linee attraverso formule spiegabili facilmente… Cadremmo in un vero e proprio corso di cosmologia. Abbiate pietà di me!
Le linee blu tratteggiate a sinistra mostrano le linee di Universo per oggetti che OGGI si trovano a 8, 16 e 46 miliardi di anni luce. Le linee puntinate a destra mostrano dove l’espansione è 2c, c e c/2 (l’espansione c corrisponde alla distanza di Hubble). La linea rossa è il nostro cono di luce passato (dove si trovano tutti gli oggetti che vediamo oggi). Notare che per i primi 4 miliardi di anni, la luce si allontana da noi, trascinata via dall’espansione. Ovviamente la linea attraversa la distanza di Hubble dove l’espansione è uguale a c. Poi inizia ad avvicinarsi. Notare anche che il cono di luce arriva, a noi, ADESSO, con linee a 45°, dato che localmente l’espansione è praticamente uguale a zero. Il redshift z e la distanza comovente (di adesso) sono indicate a destra e a sinistra. Ovviamente le linee di Universo incontrano il cono di luce nei rispettivi valori della distanza comovente.
Vi prego, però, di non cominciare a fare domande per avere spiegazioni dettagliate... Prima o poi ne riparleremo, ma per adesso.... ARRANGIATEVI da soli andando a spulciare nell'archivio... La spettroscopia, l'atomo, la matematica e il momento angolare aspettano... (*)
Volevo, inoltre, dire ad Alvy, e a chi la pensa come lui, che sono pienamente d’accordo sul fatto che un quadro generale dello Spazio-Tempo è fondamentale (non per niente ho picchiato sempre duro sul cono di luce & Co.), ma esso rappresenta lo sfondo del Teatro. Non possiamo, però, dimenticarci degli attori, della loro vita, del loro carattere e delle loro meravigliose storie (anche le più semplici).
Buon divertimento!
(*) Nel frattempo questi argomenti, e molti altri, sono stati trattati e li trovate QUI. Se avete bisogno di una guida per trovare qualcosa di specifico o dei consigli generali su come orientarsi nel blog (o per qualunque domanda vi venga in mente di fare), potete chiedere QUI.





22 commenti
... detto anche "diagramma a foglia di gelso".
Ma dai Enzo, tu sei molto meglio di Feynman; pensa che lui non ha mai risposto nemmeno ad una mia domanda!!!
Non saprà mai cosa si è perso .....
Diciamo che è una figura abbastanza familiare
ma tu, caro SMA, sei tra i più bravi!!!!!
Visto che SMA provoca (
 ) io mi adeguo (
) io mi adeguo ( 
 ).
).
Ciao SMA, vediamo se riesco a scrivere qualcosa di sensato!
La figura è senz'altro familiare; ha però una caratteristica moooolto interessante, vale a dire la curva per v= c/2. A differenza di quella per v=c (sfera di Hubble) è infatti completamente contenuta nella figura e - se non ho preso lucciole per lanterne, nel qual caso fustigatemi pure - consente qualche interessante verifica; per esempio la stima del parametro di Hubble al variare dell'età dell'universo.
Munitomi di riga e squadra (pur tenendo conto della presumibile approssimazione delle curve) ottengo quanto segue:
t = 1,0 v=c/2 d=0,66 H=741
t = 2,0 v=c/2 d=1,50 H=326
t = 3,0 v=c/2 d=2,22 H=220
t = 4,0 v=c/2 d=2,83 H=173
t = 5,0 v=c/2 d=3,55 H=138
t = 6,0 v=c/2 d=4,11 H=119
t = 7,0 v=c/2 d=4,72 H=104
t = 8,0 v=c/2 d=5,05 H= 97
t = 9,0 v=c/2 d=5,50 H= 89
t =10,0 v=c/2 d=5,90 H= 83
t = 11,0 v=c/2 d=6,17 H= 79
t = 12,0 v=c/2 d=6,50 H= 75
t = 13,0 v=c/2 d=6,72 H= 73
t = 13,5 v=c/2 d=6,83 H= 72
Ho poi condotto una verifica prendendo i valori della sfera di Hubble (v=c) fin dove la figura lo consente ed ho trovato praticamente gli stessi valori del parametro di Hubble.
Sembra che tutto torni.
I tempi sono espressi in mld anni, le distanze in mld a/l, i parametri di Hubble in km/(s*Mpc).
Naturalmente le curve si basano sul modello di universo adottato. Nel caso specifico ho notato - sempre armato di riga e squadra - che il modello della figura si discosta un pochino dal caso di universo piatto perchè l'esponente x che definisce il fattore di scala - a=(t/T0)^x - non è stato assunto pari a 0,66 (universo piatto) ma assume valori che vanno da 0,92 (per tempi "odierni") a valori via via più bassi man mano che diminuisce l'età dell'universo, fino al valore di 0,72 per t= 5 mld anni. Sembra insomma che al modello piatto iniziale (basse età dell'universo) nella figura si sia andato man mano sostituendo un modello leggermente diverso (per tenere conto dell'energia oscura?).
Caro Enzo, spero che quanto scritto corrisponda a verità perchè ho ottenuto - per via analitica, giocando con qualche derivata - valori del parametro di Hubble in linea con quelli che ho riportato sopra e la cosa mi piace assai!!!
Se ho scritto putt ... ehm .. fesserie, l'esecuzione è in programma domattina all'alba.
caro Alvy,
non potevi che ottenere quanto è riportato in figura partendo dai suoi dati... D'altra parte se prendi una velocità d'espansione costante è ovvio che la legge di Hubble porti a valori diversi di H0 cambiando la "distanza". Non capisco esattamente cosa pensavi di trovare... Colpa mia sicuramente, ma non capisco realmente qual'era lo scopo finale...
Piuttosto, ti proporrei di fare un esercizio più utile (forse): perché non trasformi la figura, mantenendo il tempo normale, ma inserendo le coordinate comoventi? Ritengo sia molto più istruttivo...
Comunque, è un discorso che non posso e non voglio approfondire (almeno per adesso). Soprattutto in uno scambio di commenti. E' come chiedere di spiegare la cosmologia attraverso bocconcini di informazione. Quella figura l'ho inserita solo per riassumere i concetti generali e il significato delle grandezze che si usano "normalmente". Per il 90% l'ho inserita per te e per darti proprio la possibilità di verificare e controllare le idee che già hai abbastanza chiare. Però non ricavando cose già insite nella curva tracciata... E' ovvio che se trovi H0 con la curva c/2, trovi lo stesso per c e per 2c. Chi comanda il tutto è solo e soltanto il cono di luce...
Molto più importante è che tu abbia ottenuto gli stessi risultati per via analitica. Ma quella è una parte che per il momento, come già detto non posso e non voglio affrontare. Questo non deve essere un corso di cosmologia, ma deve solo far capire cosa comporti a grandi linee un universo in espansione. Tutti coloro che sono in grado possono andare più a fondo, ma non è il posto per esibire calcoli superiori.
Spero di essere stato compreso.
Tu puoi benissimo andare oltre, ma soprattutto trasformando le coordinate. Te lo consiglio vivamente, anche perché con le coordinate comoventi molte cose si fanno ancora più chiare...
OK, grazie Enzo
Comunque Enzo, riguardo a ciò che speravo di trovare, c'è appunto il valore del parametro di Hubble i cui valori non ho mai visto da nessuna parte. Il fatto poi che i valori riscontrati nella figura siano molto vicini a quelli ottenuti per via analitica conferma la correttezza dell'approccio matematico.
Tutto qui.
Piano piano, passetto dopo passetto, bocconcino dopo bocconcino (per usare la tua citazione) credo di essermi chiarito le idee su alcuni punti un pò ... spinosi.
Adesso proverò a giocare con le coordinate comoventi.
Grazie di nuovo
Alvy avevo detto che è una figura familiare in quanto seguendo Enzo da parecchio tempo ho ritrovato questo grafico diverse volte, anche nel libro "L'Infinito Teatro del Cosmo", in cui è spiegato tutto molto bene.
Sinceramente non mi sono mai addentrato nei calcoli complessi, esclusa la "formuletta" di Hubble e poche altre, dato che al momento mi basta comprendere i concetti base, senza complicarmi la vita con elucubrazioni mentali che a volte possono generare confusione in noi poveri comuni mortali
Visto che sei appassionato di questo argomento (che anche a me piace tantissimo) ti consiglio questo libro appena uscito "Universo Matematico" di Max Tegmark, uno dei più autorevoli cosmologi in circolazione.
Ricevuto grande SMA.
Senti SMA, non voglio certo fare il professore, non ne ho nè i titoli, nè la capacità, nè la filosofia di vita. Se ti ho un pò infastidito scusami, volevo solo essere spiritoso .
.
Riguardo alla cosmologia, è vero, è un argomento che mi affascina ... mi fa letteralmente girare la testa, quindi ti ringrazio infinitamente per il suggerimento.
Per farmi perdonare tra qualche giorno chiederò ad Enzo di mettere in evidenza un sorprendente documento vietatissimo ai minori.
Ciao e grazie di nuovo.
Caro Enzo, ho provato a trasformare le coordinate in coordinate comoventi.
Il sistema che ho usato è sostanzialmente quello descritto negli articoli su infinito, zero, rotaie, ecc....
In quel caso si trattava di annullare l'effetto prospettico che mostrava una differente distanza tra i due binari, man mano che questi risultavano più lontani da noi.
In realtà la distanza tra i due binari non può cambiare (a meno di non voler far deragliare un treno), si tratta di un effetto apparente e l'uso delle coordinate comoventi restituisce la reale rappresentazione dei binari.
In questo caso, invece, le coordinate comoventi “annullano” l'espansione dell'universo, ma restituiscono una rappresentazione apparente delle distanze, mostrando anche quanto queste siano fittizie (soprattutto se non si specifica a cosa si riferiscono).
http://www.astrobin.com/full/105411/P/
Il cono di luce è tornato quello classico delle rette inclinate di 45° ed al tempo zero non si trova più un punto di dimensioni infinitesime, ma una retta di dimensioni infinite.
Le distanze indicate in alto sono quelle attuali (di un ipotetico istante T), con l'orizzonte dell'universo osservabile di raggio 46 miliardi di anni luce
Ovviamente le distanze “iniziali” proprie riportate in basso nella figura contenuta nell'articolo, perdono di significato, nel nuovo grafico.
L'idea di distanza assume un significato diverso, dato che con lo scorrere del tempo lo spazio aumenta di volume (e le "distanze" cambiano in continuazione).
Fortunatamente la velocità della luce è costante ed il redshift (valore di Z) rappresenta un ottimo indicatore del tempo che luce ha impiegato per giungere fino a noi.
Il tempo impiegato dalla luce per giungere fino a noi, non rappresenta la distanza tra noi è l'oggetto... e poi quale distanza dovrebbe rappresentare?
Quella di quando la luce è partita?
Quella attuale?
Grazie a Z, però, è possibile calcolare le due distanze citate prima, “misurate" in tempi diversi, quando la luce è partita e quando è arrivata .
Per esempio, ammettiamo di osservare due lontane galassie, entrambe con il medesimo redshift (la luce ha impiegato lo stesso tempo per raggiungerci) che apparentemente sembrano distare tra loro 3 miliardi di anni luce.
Tale distanza si riferisce ovviamente a quella di quando la luce è partita.
Ammettiamo che la luce sia partita quando l'universo aveva circa 3 miliari di anni (che dovrebbe corrispondere ad un valore di Z = 1,78)
Quale sarebbe la distanza attuale tra le due galassie?
Con le rotaie, per ricavare la distanza reale tra i due binari, si usava la relazione:
dn/d = sn/s
dn (distanza reale tra i binari, un po' come la distanza attuale tra le due galassie);
d (distanza apparente tra i due binari, come la distanza tra le galassie quando la luce è partita);
Sn (distanza di dn da un punto P, punto dove i due binari sembrano congiungersi, un po' come accade con il punto iniziale che “rappresenta” l'inizio dell'universo, per cui il tempo attuale, ossia 13,7 miliardi di anni );
Sn (distanza di dn dal punto P, ossia la distanza temporale tra l'inizio dell'universo, e l'epoca in cui la luce delle due galassie è partita).
Dalla relazione iniziale si ricava che: dn = d (sn/s)
(sn/s) rappresenta il coefficiente di proporzionalità da applicare a d per ricavare il valore di dn.
Nel nostro caso tale coefficiente rappresenta proprio l'espansione dell'universo con lo scorrere del tempo (il motivo per cui la luce impiega più tempo per effettuare il medesimo tragitto).
Volendo, almeno per valori di redshift non troppo elevati, è possibile usare come coefficiente di proporzionalità : (Z+1).
Sostituendo tale valore, è possibile ricavare la distanza attuale a cui dovrebbero trovarsi attualmente le due galassie:
Dato che dn = d (sn/s)
D attuale = D iniziale (Z+1)
D attuale = 3.000.000.000 (1,78 +1 ) = 8,34 miliardi di anni luce
Questa dovrebbe essere l'attuale distanza tra le due remote galassie.
Ovviamente si può anche fare il percorso al contrario, ossia ricavare la distanza iniziale, partendo da quella attuale:
D iniziale = D attuale/(Z+1)
Un po' come partire dalle coordinate comoventi (intese come distanze attuali) per ricavare la distanza iniziale (quella quando la luce è partita).
Ho anche provato a raffigurare questa trasformazione inversa, almeno per come graficamente me la immagino (con la retta che deve tornare ad essere un punto e il cono che si trasforma in un curva che sembra un uovo).
http://www.astrobin.com/full/105411/Q/
Spero di non aver detto qualche o troppe sciocchezze.
Paolo
cari Alvy e SMA,
perfetto... avete capito perfettamente lo spirito. Dato il via, poi ognuno può approfondire quanto vuole. Io, però, mi devo limitare ai concetti... ma vedo che per Paolo sono stati sufficienti e questo mi tira su e mi da molta speranza per la mente umana
caro Paolo,
ancora una volta devo ammettere che sei straordinario e dubito sempre di più che tu non sia un ricercatore in incognito...
C'è solo un piccolo errore. La figura che hai fatto tu, deve assumere anche un tempo particolare. Ma andremo a fondo magari più in là... In parole povere, se usi il tempo normale e le coordinate comoventi ottieni un cono di luce non proprio triangolare ma un qualcosa che si allarga verso il basso. Tuttavia, è più che sufficiente, anche perché l'ho usata spesso anch'io e il concetto rimane tale e quale. Se provi ad andare a guardare gli articoli che avevo scritto riguardo a "perché il Big Bang si vede dappertutto?" vedrai la variazione del cono di luce...
Comunque, hai capito benissimo il concetto di fondo
Ma, lasciami dire, che mi hai reso veramente felice! Sei riuscito a legare il concetto delle rotaie a quello dell'Universo. Sembra facile (a posteriori), ma mi hai dimostrato che le scelte che ho fatto sono state giuste. No, non è assolutamente una cosa banale... lasciatelo dire! E capisco anche che parlar di matematica in modo elementare riesce a predisporre la mente ad argomenti di ben altra portata!!!
Grazie a tutti ragazzi, SIETE FANTASTICI. Non potevo sperare di meglio
Cari tutti... stamattina vi infilo una news che potrebbe essere il vostro futuro (per i più giovani...). Chissà... a me stimola molto...
Caro Enzo, ho solo provato ad applicare i concetti che hai espresso in diversi tuoi articoli....
Ti confesso che ho postato tutto solo a tarda notte, proprio per l'incongruenza tra scala del tempo e cono di luce.
Problema che ho solo nascosto sotto al tappeto indicando sull'asse del tempo solo la tacca riferita a 14 miliardi dall'inizio dell'Universo.
Ho pensato e ripensato come affrontare il problema senza giungere a conclusioni certe.
Il problema io lo inquadro cosi:
Problema 1) Se c è costante, dato che c non è altro che la quantità di spazio (1 anno luce) percorsa in un unità di tempo (1 anno), ossia c = S/T, mantenendo lo spazio costante nel tempo (distanze comoventi), affinchè c rimanga costante devo mutare il Tempo, o meglio la sua scala.
Ovviamente questa diverso scorrere del tempo è solo apparente, un po' come accade con un effetto ottico;
Problema 2) La curva descritta dal cono di luce (nella figura iniziale dell'articolo) mostra un andamento non lineare, dello spazio in funzione del tempo.
In maniera esclusivamente intuitiva, penso che sia necessario utilizzare una scala del tempo in funzione di Z (dato che è il nostro indicatore del tempo impiegato dalla luce per raggiungerci).
Ho anche pensato di sostituire Z al posto di T, applicando alle distanze comoventi (attuali) la formuletta per ricavare la distanza reale
http://www.astrobin.com/full/105411/R/
Però, non sono in grado di indicare sull'asse delle y i valori di Z e continuo a nutrire dubbi sulla rappresentazione del cono di luce.
Mi sembra decisamente più calzante la modifica del cono di luce che hai mostrato nell'articolo conclusivo “perchè il Big Bang si vede dappertutto”.
Sono fuori strada con questi ragionamenti?
In ultimo, dall'incognito diario di un ricercatore di conoscenza, privo di titoli e lauree:
“Dopo una prima sommaria lettura, sto rileggendo gli articoli di Enzo (il Druido) sulla matematica.
In questa seconda fase, può capitare di rileggere parti dell'articolo anche diverse volte..... finché non risulta chiara la radice del ragionamento ed il metodo di lettura proposto.
Non contento cerco di sviluppare il ragionamento, inventandomi problemi e soluzioni, cercando di colmare le lacune in geometria con Photoshop, con visualizzazione di una griglia che lo rende simile ad un carta millimetrata.
Prima di lanciarmi in enunciazioni, laddove possibile cerco conferma dei risultati ottenuti con qualche calcolo, controllando i risultati con la figura realizzata (così posso confrontare la mia scarsa visione geometrica del problema con quel poco di matematica che ho provato ad applicare).
Le mie lacune in geometria piano piano sembrano svanire..... e la matematica assomiglia sempre più ad una lingua, con le sue regole grammaticali, capace di descrivere fenomeni, analizzarli, scomporli e ricomporli, costruendo a volte inediti mosaici.....
Come mi piacerebbe conoscere a fondo questo linguaggio (per ora balbetto qualcosa), costruendo poetiche visoni delle infinite meraviglie che ci regala il teatro del cosmo”.
Paolo
caro Paolo,
ancora una volta sei arrivato velocemente al nocciolo del problema. Hai praticamente già dato la soluzione per la tua figura. E' proprio ciò che vedi nell'articolo che citi riguardo all'ultima figura (quello sul Big Bang visto ovunque). Per avere quella precedente (quella che disegni anche tu) devi cambiare il tempo (come tu stesso dici). Questo tempo si chiama conforme ed è costretto a scorrere in modo diverso dato che deve riuscire a mantenere le distanze invariate in un qualcosa che si dilata sempre più. Esistono formule per calcolarlo, ma direi che non è il caso di andare oltre. L'importante è che tu abbia capito il vero problema. Se vuoi raddrizzare il cono di luce (oltre che rendere parallele le linee di Universo) devi deformare anche il tempo e crearne uno nuovo come hai fatto per la distanza comovente... Comunque, il fatto di aver capito cono di luce, coordinate comoventi e trasformazioni varie è già un risultato prodigioso. Pensa che tanti laureati ingegneri rifiutano anche solo di avvicinarsi al cono di luce, considerandolo IMPOSSIBILE da capire...
Riguardo alla seconda parte che dirti? sarebbe da inserire all'inizio di ogni libro di matematica!!!! Tu non sai quanto mi fai felice...
Caro Enzo, ho seguito l'interessante dibattito con l'ottimo Paolo.
Direi che mi torna un pò tutto. Sollevo però una questione di metodo.
Una volta digerite le distanze comoventi (distanze fittizie basate sull'idea che lo spazio non si espanda mentre invece lo fa) ed il tempo conforme (un tempo fittizio che scorre in modo ... anomalo) mi sfugge il vantaggio che hanno gli scienziati ad adottare detti riferimenti.
Capisco che anche le distanze "fisiche" dipendono dal modello adottato e lo scorrere del tempo dipende dall'osservatore ma, dovendo comunque scegliere dei riferimenti di base, mi sembra meno cervellotico l'utilizzo di questi ultimi.
Insomma, dov'è il vantaggio? Non mi dire che dipende dal fatto di avere distanze immutabili perchè lo si paga a caro prezzo, almeno così mi sembra, o no?
Ciao, grazie e buona domenica.
caro Alvy,
il vantaggio, che si vede chiaramente in una figura decisamente più regolare e facile da tracciare, si ripercuote nelle formule matematiche che usano questi parametri. Certi tempi e certe distanze rimangono costanti o variano in modo lineare. Bisognerebbe entrare nelle descrizioni dei vari spazi utilizzati e i vantaggi verrebbero fuori chiaramente. E' un po' come quando per risolvere certi sistemi o integrali si fanno cambiamenti di coordinate...
Buona domenica anche a te!
Enzo, ma stai facendo di Paolo un "mostro" della cosmologia!


Ovviamente in senso buono, anzi stra buono!
Purtroppo in queste settimane non potrò inserirmi nel dibattito perchè non ho tempo sufficiente per argomenti di questo spessore, però mi sarebbe piaciuto vedere dove riuscivo ad arrivare (anche se ben lontano da Paolo)...
Comunque una domanda un filo fuori tema ma che mi può essere utile, ma che programma usate tu e Paolo per fare i disegni e i diagrammi? openoffice?
Ciao Alexander, io uso Photoshop per realizzare i grafici.
Per mostrizzarmi sto solo leggendo approfonditamente gli articoli sulla matematica e sulla struttura dello spazio-tempo che ha scritto Enzo.
Ti assicuro, però, che non vi è nulla di mostruosamente difficile, gli ingredienti sono tutti lì a disposizione di tutti, ci vuole solo un pò di costanza per trovare il proprio modo di cucinare.
Personalmente sono convinto di conoscere pochissimo e che ci sono moltissime cose da capire e imparare..... tra l'altro, spesso, si capisce a fondo qualcosa proprio quando altri ti fanno notare gli errori, che altrimenti rischi di trascinarteli all'infinito.
Paolo
assolutamente d'accordo con te!
Se non si ha almeno una conoscenza minima (direi elementare) e l'umiltà di imparare, accettando e prendendo atto delle proprie lacune, si rischia davvero di ritrovarsi a commettere errori concettuali veramente gravissimi....
MQ e cono di luce (solo per dirne 2) mi hanno insegnato tantissimo e ho riparato a molte idee del tutto sbagliate che mi ero creato...
Bravissimi ragazzi.... parole sante!!! Preferisco scrivere che imparare programmi nuovi... non prendetemi come esempio per questo, però...
Preferisco scrivere che imparare programmi nuovi... non prendetemi come esempio per questo, però... 
Io, se non trovo figure già fatte (ma spesso non è facile), me le costruisco con power point... Sono proprio antiquato, ma mi diverto parecchio...