E’ ora di tornare alla nostra matematica, dato che molti l’hanno seguita e vorrebbero proseguire. Abbiamo iniziato a studiare le funzioni e torniamo improvvisamente indietro a parlare di nuovo di retta, la funzione più semplice e la prima che abbiamo trattato… Sembrerebbe una cosa assurda.

In realtà, un po’  lo è per davvero. Certe considerazioni potevano essere fatte a suo tempo. Tuttavia, la scelta non è casuale… Avessimo continuato con altre nozioni sulla retta, che, allora, sarebbero  sembrate fini a se stesse, saremmo caduti in una matematica apparentemente noiosa e ripetitiva. Molto meglio parlarne ora in modo da vedere subito un’applicazione pratica di quanto stiamo per descrivere.

La ragione è abbastanza semplice. Per studiare i punti di flesso obliquo è utile determinare la retta tangente in tali punti. Se ciò è stato facilissimo per i massimi, i minimi e i flessi orizzontali (la tangente è sempre una retta parallela all’asse delle x, dato che la derivata è uguale a zero), è leggermente più complicato per quelli obliqui. Roba da poco, ma che ci dà lo spunto per chiacchierare ancora un po’ attorno alle rette e descriverle in modi leggermente diverso da quanto fatto finora. Niente di veramente nuovo, ma che conviene riassumere e raggruppare.

Malgrado la retta sia la funzione più semplice, continua sempre ad avere risvolti non banali.

Retta passante per un punto

Il problema che ci poniamo è piuttosto banale, ma è bene affrontarlo. Dato un certo punto P(x₀,y₀) quali sono le equazioni delle rette che passano per quel punto? Ovviamente le rette sono infinite. Basta disegnarne una e poi farla girare attorno al punto fissato e si ottiene ciò che viene chiamato in gergo, un fascio di rette, come mostrato in Fig. 1. Beh, sì, sembra proprio un fascio di grano o qualcosa del genere. Essendo infinite, la loro equazione non può determinare una sola retta, ma deve avere un parametro libero che le permetta di … girare. In parole povere, scrivere l’equazione di una retta passante per un punto vuol dire scrivere quella di tutte le rette del fascio.

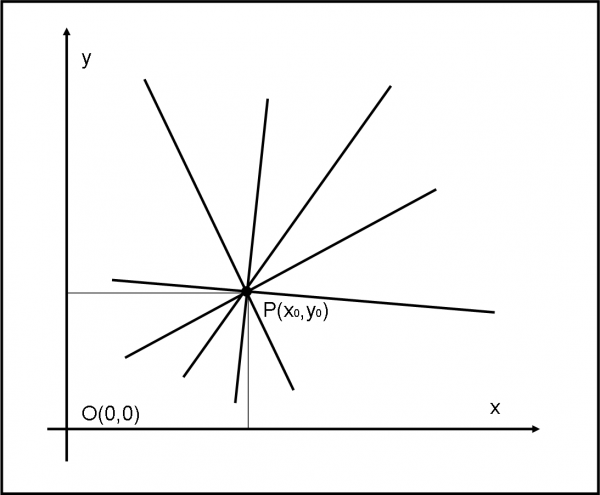
Vi sono vari modi per ottenere il risultato. Ne riportiamo due, anche se, in fondo, sono la stessa cosa…

Tracciamo una retta qualsiasi del fascio di rette, di cui vogliamo trovare l’equazione. Qual è l’equazione generica di una retta? La conosciamo bene. Essa vale:

y = mx + n    …. (1)

dove m è l’ormai celebre coefficiente angolare (ossia la tangente trigonometrica dell’angolo tra retta e asse delle x, ma anche la derivata della retta… ricordate? y’ = m). Come si vede bene la retta ha due parametri variabili (m e n). Dobbiamo fissarne almeno uno per lasciare l’altro libero di far girare la retta attorno al punto.

Sappiamo, comunque, che la retta qualsiasi deve passare per il punto P, ossia le coordinate del punto devono soddisfare l’equazione precedente. Deve perciò valere:

y₀ = mx₀ + n    …. (2)

Ricaviamo n:

n = y₀ – mx₀

Adesso, possiamo tranquillamente andarlo a sostituire nell’equazione generica (1) e otteniamo:

y = mx + n  =   mx + y₀ – mx₀

Sistemiamola un po’ e otteniamo l’equazione desiderata:

y – y₀ = m (x – x₀)    …. (3)

Infatti, l’unico parametro rimasto libero è proprio m, quello che, variando, fa girare la retta attorno al punto P.

Potevamo arrivare allo stesso risultato in altro modo, proprio scrivendo il coefficiente angolare. Usiamo, per chiarezza, la solita Fig. 2. Inseriamo il punto P e tracciamo una retta qualsiasi passante per P. Su di lei prendiamo un punto Q qualsiasi di coordinate x e y. Si identifica immediatamente anche il punto R(x,y₀). Dal solito triangolo rettangolo PRQ si ha:

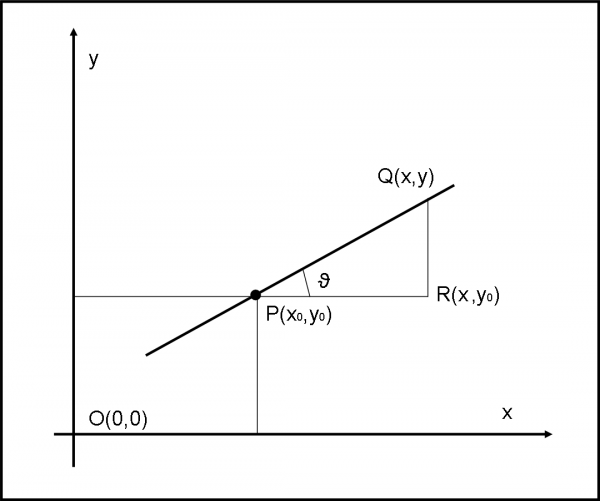
QR/PR = (y – y₀)/(x – x₀) = tan (ϑ) = m

da cui:

(y – y₀)/(x – x₀) = m

E, nuovamente:

y – y₀ = m (x – x₀)

Vogliamo fare un semplice esempio? Poniamo P = P(2, 3)

La (3) diventa:

y – 3 = m (x – 2)

Questa equazione descrive il fascio di rette passante per P(2, 3). Al variare di m si ottengono tutte le rette del fascio.

Insomma, un problemino di facilità irrisoria che potevamo già risolvere molti articoli fa (e tra le righe l’avevamo già fatto).

Retta per due punti

Cosa bisogna avere in più per potere determinare una e una sola retta nel fascio che abbiamo appena definito? Un’altra condizione che ci permetta di determinare il valore di m (l’unica incognita nella nostra equazione). In altre parole, è come se il fascio fosse una girandola e noi la bloccassimo con un dito…

Beh… la cosa più facile sarebbe dare un altro punto che appartiene alla retta che vogliamo descrivere. Sappiamo benissimo, infatti, che per due punti passa una e una sola retta!

Non ci resta che provare e vedere come si scrive la retta finale. Consideriamo un punto S (x₁, y1) che appartenga anch’esso alla retta. Riprendiamo il nostro fascio di rette che aveva come equazione:

y – y₀ = m (x – x₀)

Possiamo agire come prima e inserire le coordinate del nuovo punto  nell’equazione precedente. Ovviamente, queste coordinate devono soddisfare l’equazione dato che il punto sta sulla retta:

y₁ – y₀ = m (x₁ – x₀)

Come dovevamo aspettarci, l’incognita è ora una sola e otteniamo subito:

m = (y₁ – y₀)/(x₁ – x₀)

Beh… è un risultato che dovevamo aspettarci! Sappiamo benissimo che il coefficiente angolare di una retta è proprio dato dal rapporto tra le ordinate e le ascisse di due suoi punti qualsiasi e quindi anche dei due punti P e S.

L’equazione di una retta per due punti diventa:

y - y₀ = (x – x₀) (y₁ – y₀)/(x₁ – x₀)        …. (4)

o, se preferite:

(y- y₀) /(y₁ – y₀) = (x – x₀) /(x₁ – x₀)     …. (5)

Vogliamo fare un semplice esempio? Consideriamo P(2,3) e S(5,7). La retta che passa per questi due punti diventa:

(y - 3)/(7 - 3) = (x – 2)/(5 - 2)

Un po’ di calcoli…

(y – 3)/4 = (x – 2)/3

E ancora:

3 (y – 3)  = 4 (x - 2)

3y – 9 = 4x – 8

3y = 4x - 8 + 9 = 4x +1

E infine:

y = (4/3) x + 1/3

Usiamo la derivata

Abbiamo usato il metodo più banale per  scegliere una sola retta tra quelle appartenenti a un fascio. Le cose si fanno più interessanti se il nostro fascio di rette ha come “centro” un punto P che appartiene a una certa funzione y = f(x). Se volessimo scegliere proprio quella che è tangente alla funzione? Avremmo veramente bisogno di un altro punto per definire questa retta? Certamente no.

Sappiamo ormai benissimo che la tangente a una funzione (ossia a una certa curva qualsiasi), in un suo punto, è una retta che ha per coefficiente angolare la derivata della funzione calcolata in quel punto. Ma, allora, abbiamo due condizioni per poter scrivere la retta tangente: la prima è, ovviamente, il passaggio per il punto P (ossia deve appartenere al fascio di rette passanti per P); la seconda è che il valore di m  non è altro che la derivata della funzione calcolata in P.

Cosa ci dice questa semplice doppia operazione? Un fatto molto importante.

Data una certa funzione y = f(x) siamo in grado di scrivere l’equazione delle rette tangenti alla funzione in ogni suo punto. Basta scrivere, punto per punto, il fascio di rette che passano per il punto e poi imporre, di volta in volta, che il coefficiente angolare sia la derivata di f(x) calcolata nel punto. Pensateci bene… è un risultato banalissimo, ma di grandissima utilità, come vedremo nel caso dei flessi obliqui.

Descriviamo le operazioni ds svolgere.

La funzione sia y = f(x), il punto P della curva dove vogliamo tracciare la tangente sia P(x₀, y₀).

Innanzitutto, scriviamo il fascio di rette che passa per P:

y = m(x - x₀) +  y₀

Poi, eseguiamo la derivata della funzione, ossia f ’(x), e calcoliamola nel punto P, ottenendo f ’(x₀). Questo numero non è altro, però, che il coefficiente angolare della retta tangente a f(x) in P, e quindi dobbiamo inserirlo al posto di m nella retta del fascio precedente. Otteniamo

y = f’(x₀)(x – x₀) + y₀       …. (6)

La tangente è completamente determinata!

Facciamo subito un esempio.

Consideriamo come funzione quella di una parabola (ad esempio):

y = 2x² – 3x + 5

e, come punto in cui vogliamo calcolare la tangente, P(2, 7)

Siamo sicuri che il punto appartenga alla curva? Provate a verificarlo! Io dico di sì…

La retta generica passante per il punto P(2,7) ha equazione:

y = m (x - 2) + 7

Adesso, basta calcolare la derivata della funzione nel punto P.

y' = f '(x) = 4x – 3

f ’(2) = 4 (2) – 3 = 5

Questo numero non è altro che il coefficiente angolare della retta tangente e quindi lo inseriamo al posto di m nella retta del fascio. Otteniamo:

y  = m(x – 2) + 7 = 5 (x - 2) + 7

Qualche passaggio algebrico…

y = 5x – 10 + 7 = 5x - 3

Magnifico! La retta y = 5x – 3 è proprio la tangente alla funzione y = 2x² – 3x + 5   nel punto P(2,7).

Ci torneremo sopra quando parleremo di flessi obliqui, ma, in generale, possiamo divertirci a scrivere l’equazione delle  tangenti in un qualsiasi punto di una qualsiasi funzione

Se lo facessimo nei punti di massimo, minimo e flesso orizzontale troveremmo, ovviamente, delle rette che sono parallele all’asse delle x.

Retta perpendicolare a un’altra retta

Questa parte non interessa direttamente lo studio di una funzione. Tuttavia, potrebbe venire utile quando si traffica con i vettori e i versori e si vogliono costruire quelli perpendicolari tra loro. Chissà mai…

In poche parole, vogliamo scrivere l’equazione di una retta perpendicolare a un’altra retta. Ci sono nuovamente due possibilità: o una retta qualsiasi tra le infinite rette perpendicolari a una retta data o scegliere proprio quella che è perpendicolare a quella di partenza in un punto ben definito.

Cominciamo con una qualsiasi perpendicolare. Ci serviamo della Fig. 3

Per semplicità di calcolo (ma potevamo sceglierle dovunque), facciamo passare entrambe le due rette perpendicolari tra loro proprio dall’origine degli assi. In fondo, a noi interessa solo trovare la relazione che esiste tra m e m’. Sono loro che indicano la direzione delle rette. Tracciamo la perpendicolare all’asse x nel punto H che abbia ascissa uguale a 1 (qualsiasi sia l’unità di misura). Ossia OH = 1.

Possiamo scrivere subito (per definizione di m e m’) che:

m = tan (ϑ) = QH/OH = QH

m’ = tan (- ϑ’) = - tan (ϑ’) = - SH/OH = - SH

m’ assume un valore negativo, dato che abbiamo considerato l’angolo negativo. Scriviamo:

SH = - m’

Consideriamo adesso il triangolo rettangolo (per definizione) OHS. Per il secondo teorema di Euclide si ha:

OH² = QH ∙ SH

Non ve lo ricordate? Poco male… si ricava subito dai due triangoli simili OHQ e OHS, scrivendo la proporzione:

QH : OH = OH : SH

E, dato che il prodotto dei medi è uguale al prodotto degli estremi:

OH² = QH ∙ SH

Come volevasi dimostrare…

Adesso, basta sostituire e si ha:

1² = 1 = - m ∙ m

Da cui:

m’ = - 1/m     …. (7)

Questa è la relazione che lega tra loro due rette perpendicolari. Ossia, data una retta qualsiasi, le rette ad essa perpendicolari devono avere come coefficiente angolare l’inverso del coefficiente angolare della retta di partenza cambiato di segno.

In parole matematiche…

data la retta

y = mx + n

le perpendicolari a questa retta generica hanno equazione:

y = - x/m + n’    …. (8)

In particolare, è utile trovare la retta perpendicolare a una retta in un suo punto, ad esempio P(x₀, y₀). Beh… dovremmo già sapere come agire. Scriviamo il fascio di rette che deve contenere sia la retta di partenza che quella a lei perpendicolare (passano entrambe per il punto P).

La retta di partenza sia:

y = m₀x + n₀    (m₀ e n₀ sono termini noti)

e il suo punto P (x₀, y₀).  Scriviamo subito il fascio di rette passanti per P:

y – y₀ = m(x – x₀)

La retta perpendicolare alla retta di partenza nel punto P(x₀, y₀) deve appartenere al fascio e avere m = -1/m₀

Basta allora scrivere:

y – y₀ = -1(x – x₀)/m₀       …. (9)

che ci regala l’equazione della retta perpendicolare a quella di partenza (nota) nel punto P(x₀,y₀).

Facciamo un esempio semplicissimo.

La retta di partenza sia y = 3x – 2

Il punto P sia P(2,4)   (controllate sempre che sia proprio un punto della retta….).

Scriviamo  il fascio di rette passante per P

y – 4 = m (x – 2)

e poi al posto di m inserisco -1/m₀ = -1/3

Ottengo:

y – 4 = -1/3 ･( x – 2)

Qualche passaggio …

y – 4 = - x/3 + 2/3

y = - x/3 + 2/3 + 4 = - x/3 + 14/3

Lascio a voi provare a scrivere l’equazione della retta perpendicolare alla retta y = 3x – 2 e passante per un punto esterno alla retta, ad esempio Q (1, 5) (che non appartiene alla retta, verificare….).

Basta scrivere il fascio di rette passante per Q e poi imporre che il coefficiente angolare sia uguale all’inverso cambiato di segno del coefficiente della retta di partenza (y = 3x – 2). Un gioco da ragazzi…

Possiamo fermarci qui, dato che a noi interessa solo poter trattare le rette tangenti nei punti di flesso e siamo già andati oltre.

Una retta può, però, dare spunto a molti altri “giochini”, come, ad esempio, scrivere la parallela a una retta data, passante per un punto esterno, oppure scrivere la tangente a una funzione data, a partire da un punto esterno alla funzione. Insomma, una semplice retta ci permette di divertirci in tantissimi modi… Basta riflettere e provare…

Lasciamo la geometria e torniamo alle nostre funzioni

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica