Per una trattazione completa, inserita in un contesto più ampio, dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Prima di andare a vedere cosa succede nelle superfici stellari a causa delle particelle libere di giocare i loro scambi energetici senza essere disturbate da troppi vicini di casa (le righe spettrali), parliamo anche un po’ di colore. Sì, proprio il colore dell’arcobaleno.

Newton (e non solo lui) ci ha mostrato che al variare della lunghezza d’onda varia anche il colore che l’occhio riceve. Sappiamo anche che il nostro occhio copre solo un piccolissimo intervallo dello spettro elettromagnetico. Potremmo dire che esistono colori, ossia lunghezze d’onda, che non possiamo associare a niente di fisicamente recepibile dai nostri sensi. Fortunatamente, l’uomo ha costruito occhi che vedono anche i “colori” relativi a lunghezze d’onda sia cortissime  che grandissime.

Tuttavia, per definire la temperatura di una stella può già bastare osservare lo spettro nel visibile. E non c’è nemmeno bisogno di ottenere tutto lo spettro (ricordate il breve inciso che avevamo inserito sulla giusta temperatura delle stelle?). Basta fissare due lunghezze d’onda (ad esempio quella del blu e quella del rosso) e fare la differenza di luminosità. In effetti, due spettri relativi a due stelle di diversa temperatura si spostano uno rispetto all’altro, abbassandosi o alzandosi a seconda della posizione del loro picco. (Ricordiamoci le due leggi di Stefan-Boltzmann e di  Wien).  Ciò vuole anche dire che se facessimo la differenza tra la luminosità nel blu e quella nel rosso avremmo, nei due casi, valori diversi.

Siamo piuttosto fortunati! Non solo le stelle emettono soprattutto nel visibile, ma non esistono differenze di due colori (scegliendoli bene, ovviamente) che coincidano, se gli spettri sono diversi. Ciò vuol dire che basta considerare questa differenza (indice di colore) al posto della temperatura. Conosciuto l’indice di colore si risale allo spettro corrispondente e quindi alla temperatura. Nella Fig. 1 vediamo due spettri e il relativo indice di colore B-V.

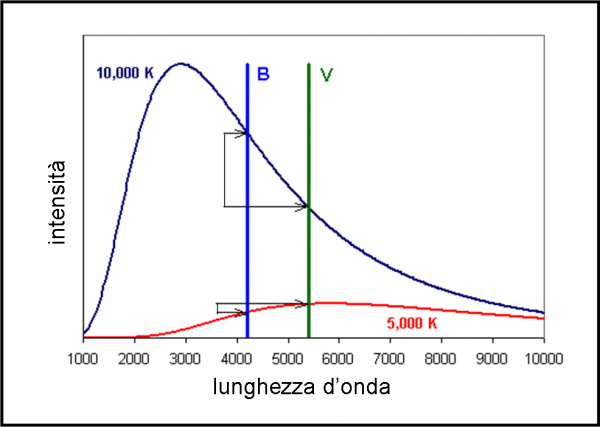
Perché tanta fatica? Perché non sempre è possibile ottenere uno spettro, dato che l’intensità della luce dipende dalla distanza. E’ molto più facile misurare la luminosità in due soli colori (o lunghezze d’onda, ricordiamolo sempre). Il risultato è, però, quasi lo stesso, dato che da questa differenza si può approssimativamente risalire alla temperatura e al diagramma HR precedente. Ecco perché tante volte si vede in ascissa sia l’indice di colore che la temperatura o anche il colore della stella (relativo al punto di massimo dello spettro, che a sua volta è legato alla temperatura).

Bene, le stelle cominciano a essere comprensibili attraverso la loro temperatura e luminosità. Grazie ai fotoni le informazioni sono ben più di quelle che uno si aspetterebbe guardandole a occhio nudo. Tutto ciò grazie al corpo nero e -soprattutto- alla tecnica della spettroscopia.

Tuttavia, le informazioni contenute nella luce sono ben più numerose. Per andare avanti dobbiamo, però, capire ancora meglio come si muovono gli elettroni, come interagiscono tra di loro e come fabbricano i loro messaggeri luminosi. Per far questo occorre dare un’occhiata alla meccanica quantistica e ai modelli più moderni dell’atomo. Oltretutto, la meccanica quantistica spiega perfettamente perché la catastrofe ultravioletta è una catastrofe solo apparente. Ciò permetterà di descrivere l’andamento dello spettro continuo con una formula perfetta. Il modello atomico si occuperà invece di quelle righe “scure” che sembrano essere solo un rumore noioso nello spettro di una stella. Sarà anche un rumore un po’ fastidioso, ma è un rumore che ci regala un numero incredibile di informazioni…

Vedremo, anche, che i due grandi iniziatori di questa decodificazione completa dell’informazione sono accomunati da una strano destino: il primo (Planck) ha tentato una spiegazione senza crederci affatto (per pura disperazione); il secondo (Einstein) l’ha verificata senza sapere che sarebbe stata l’incubo della sua vita.

L’energia viaggia a “pacchetti”

Torniamo alla ormai ben nota curva a campana e alla sua “catastrofe” ultravioletta. C’è poco da fare, le leggi della fisica classica non permettono di descrivere ciò che si osserva sperimentalmente. Ci deve essere qualcosa di sbagliato nella legge di Rayleigh-Jeans, ma non “troppo” sbagliato se no tutta la fisica precedente sarebbe da buttare al macero. E, invece, sappiamo che per moltissime cose funziona perfettamente bene.

Immaginiamo di avere uno scivolo praticamente infinito che inizi a un altezza comparabile a quella degli aerei di linea (ma anche più in alto). Vicino a lui vi è, invece, una scala che parte e arriva negli stessi punti dello scivolo. Se utilizzassimo lo scivolo, è meglio non pensare a cosa ci potrebbe succedere arrivando al suolo! La velocità acquisita sarebbe incredibile e sarebbe molto difficile raccogliere i nostri pezzetti sparsi di qua e di là. Abbiamo, infatti, acquistato un’energia cinetica enorme. Insomma, ci capita una vera … “catastrofe”. Se, invece, usassimo la scala, scenderemmo molto lentamente ma arriveremmo sani e salvi. L’energia finale sarebbe insignificante, dato che l’abbiamo rilasciata gradino per gradino e non tutta assieme nell’urto finale. Nessuna… catastrofe!

Nulla è effettivamente cambiato, ma ciò che prima sembrava infinita (l’energia) diventa invece praticamente nulla. Qualcosa di simile al corpo nero. La fisica classica (scivolo?) ci dice che a lunghezze d’onda molto corte l’energia tende a essere enorme, mentre l’evidenza osservativa (scala?) ci dice che l’energia è trascurabile. Mi raccomando, non prendete questo esempio troppo alla lettera. Serve solo per capire meglio il concetto di fondo.

L’idea, però, non è male... Perché non pensare che anche l’energia che viene rilasciata dai fotoni lavori in modo analogo? In altre parole, potremmo dire che ogni fotone porta con sé l’energia di uno scalino. Non sappiamo, ancora, perché mai dovrebbe funzionare così, ma “per disperazione” potremmo anche provare a fare questa ipotesi campata del tutto in aria, senza alcuna prova sperimentale.

Beh… possiamo anche evitare di fare i conti, dato che ci ha già pensato il signor Planck. Egli ha ipotizzato che a ogni fotone sia associata una certa quantità di energia, che ha chiamato “quanto”. In altre parole lo “scalino”. Tuttavia, gli scalini non possono essere tutti uguali, dato che la loro “altezza” (energia) deve dipendere dalla lunghezza d’onda (o frequenza) del fotone. Deve valere, perciò, una certa legge che regola il rapporto tra energia E e frequenza ν. Chi deve rimanere costante è il rapporto tra queste due quantità, ossia:

E/ν = h

h prende (giustamente) il nome di costante di Planck. Essa permette di misurare l’energia di un “quanto”  associato a una certa frequenza. Questa costante è qualcosa di estremamente piccolo e nessuno potrebbe rendersi conto sperimentalmente che l’energia si propaghi a piccoli salti, invece che in modo continuo.

Chi vede strisciare per terra un millepiedi, pensa subito che sia un verme. E, invece, guardandolo bene, si nota che è munito di moltissime zampette. Immaginiamo che ogni paio di zampette sia un pacchetto di energia. Pensate a un millepiedi con le zampette piccolissime e il gioco è fatto. Diciamo un… miliardopiedi.

Questa ipotesi, del tutto artificiosa e senza alcun legame con la fisica conosciuta, permette di evitare la catastrofe ultravioletta. In parole molto semplici: aumentando la frequenza, ogni pacchetto ha un’energia maggiore, ma diminuisce il numero di pacchetti disponibili. Andando verso lunghezze d’onda cortissime l’energia è sempre più alta, ma si hanno sempre meno pacchetti a disposizione. La probabilità che si possa “formare” un pacchetto di energia infinita è zero e quindi l’energia totale in funzione della lunghezza d’onda sale fino a un certo valore massimo per poi scendere di nuovo a zero per lunghezze troppo corte.

Notate che ho usato alternativamente lunghezza d’onda e frequenza proprio per ribadire meglio il concetto che una grandezza è inversamente proporzionale all’altra. Se una cresce, l’altra decresce.

Per una visione ancora più semplice  del concetto dei quanti (da prendere con le dovute limitazioni), immaginiamo di avere un pozzo pieno d’acqua e di volerlo svuotare. Lo possiamo fare, però, usando secchi di grandezza crescente durante intervalli di tempo sempre uguali. All’inizio i secchi sono molto piccoli. L’operazione è rapidissima, ma ogni secchiello contiene pochissima acqua. Nel tempo limite siamo riusciti a fare ben poco.

Cambiando dimensioni del secchio le cose vanno un po’ meglio: se ne riempiono di meno, ma ognuno contiene molta più acqua di prima. La quantità totale di acqua, prelevata usando il secondo secchio, è decisamente maggiore. La quantità continua a crescere aumentando le dimensioni del secchio.

A un certo punto, però, i secchi cominciano a pesare un po’ troppo e nel tempo limite riusciamo a tirarne su molti di meno della volta precedente. La quantità totale dell’acqua recuperata inizia a diminuire. Il secchio è ormai molto grande e pesantissimo: nel tempo prestabilito possiamo tirarne su pochissimi. La faccenda continua a peggiorare. Alla fine arriviamo al punto in cui il secchio è talmente grande che non riusciamo nemmeno a tirarne su uno: niente più acqua! Se segnassimo su un foglio la quantità d’acqua che abbiamo estratto dal pozzo in funzione della grandezza del secchio (o della lunghezza d'onda) ci accorgeremmo di aver descritto una curva a campana, propria quella che elimina la catastrofe.

Se, invece, usassimo una pompa aspirante di diametro crescente, troveremmo che la quantità d’acqua recuperata nell’unità di tempo crescerebbe sempre di più. Teoricamente, con la pompa giusta, potremmo prosciugare un intero lago in un intervallo di tempo cortissimo. Insomma, arriveremmo alla … catastrofe. In un caso l'acqua è stata tirata sù a pacchetti (secchi), nell'altro in modo continuo (pompa).

Ovviamente, Planck non ha usato né secchi né ha mai dovuto prosciugare un pozzo, ma è riuscito, seguendo l’ipotesi fantascientifica del pacchetto di energia, a ottenere una formula che descrive perfettamente la campana della distribuzione di energia al variare della lunghezza d’onda  (o della frequenza). Non la riporto perché è abbastanza complicata, ma vi assicuro che la descrive in modo perfetto!

La faccenda è ancora più fantastica, in quanto questa equazione permette di ricavare le leggi empiriche di Wien e di Stefan-Boltzmann. Noi potremmo anche essere po’ sorpresi di quanto ottenuto, tuttavia, il più sorpreso di tutti è stato proprio Planck che pensava a tutto ciò come a un espediente matematico, ma non certo a una soluzione fisica e reale. Sì, sì, funzionava, ma la matematica aveva descritto qualcosa senza tener conto di come funzionava la fisica. Un bel gioco, ma niente di più. Senza nemmeno volerlo, Planck aveva dato il via alla meccanica quantistica!

Il primo a dimostrare quanto questa idea fosse concreta e non un semplice gioco di prestigio, è stato proprio colui che si è, in seguito, sempre opposto ai risvolti probabilistici della meccanica quantistica, Albert Einstein.

Il grande fisico è riuscito a spiegare, utilizzando i quanti di Planck, l’emissione di elettroni da una superficie metallica che viene colpita da un fascio di fotoni, ossia da una radiazione elettromagnetica. Einstein ha stabilito che l’emissione dipende fortemente dalla lunghezza d’onda della luce incidente e ha approfittato dell’ipotesi di Planck per fornire la soluzione rivoluzionaria.

L’energia incidente non è distribuita in modo uniforme, ma attraverso pacchetti di energia, i quanti di Planck, funzioni della frequenza. I fotoni possono quindi essere considerate vere e proprie particelle che trasmettono la loro energia (variabile a seconda della frequenza) agli elettroni che vengono colpiti. Se questa energia è sufficiente, gli elettroni vengono addirittura cacciati dall’atomo. La  quantità minima di energia per riuscire in questo compito non è altro che quella descritta da Planck (ma che Einstein comunicò per primo). La conosciamo già:

E = hν

O, inserendo la lunghezza d’onda λ:

E = h(c/λ)

Dove c è la velocità della luce e h è, ovviamente, la costante di Planck.

In parole semplici, solo se il fotone è della giusta frequenza e ha la giusta energia può staccare un elettrone dal nucleo e renderlo… libero. Non solo. Se l’energia è superiore al valore limite, l’elettrone ne porta un po’ con sé sotto forma di energia cinetica e quindi può viaggiare facendo il suo slalom tra nuclei, atomi e molecole. Abbiamo descritto il celeberrimo effetto fotoelettrico.

Tutto sta tornando perfettamente con quanto descritto nelle pagine precedenti. Ogni materiale ha le sue regole, però. Infatti, l’energia di “liberazione” dipende molto dal tipo di atomo che trattiene i propri elettroni. Tutto ciò è fondamentale per creare il nuovo modello dell’atomo e descrivere la sua capacità di emettere o assorbire radiazione elettromagnetica. Come ovvia conseguenza nascono le righe spettrali che variano da materiale a materiale e il cerchio si stringe sempre più. Un processo che la QED ci ha insegnato benissimo.

Questa scoperta ha dato a Einstein il Premio Nobel e ha aperto la strada, in modo dirompente, alla meccanica quantistica. Chi è stato lo studioso che ha cercato di lottare più duramente contro la spiegazione di Einstein. Sembra impossibile: proprio Planck, colui che aveva fornito l’idea di base ad Einstein, ma che non poteva credere che la fisica classica fosse da “rivoltare” fino a questo punto. La Scienza, a volte, può portare ad assurdità incomprensibili. Tuttavia, le grandi menti lavorano con indomito coraggio, ma anche con estrema attenzione al lavoro precedente. Ci vuole il giusto tempo per accettare visioni rivoluzionarie.

Siamo arrivati a un punto fondamentale. Sappiamo come misurare la temperatura superficiale di una stella, paragonando il suo spettro continuo a quello di un corpo nero. Siamo, però, anche in grado di descrivere la struttura dell’atomo e le azioni che subisce sotto l’effetto dell’energia elettromagnetica (i fotoni con le loro lunghezze d’onda). Non sempre, infatti, i fotoni e i loro pacchetti d’energia riescono a “cacciare” gli elettroni dall’abbraccio del nucleo. A volte, possono solo spostarli da una posizione a un'altra, ma non certo in maniera qualsiasi!

Siamo giunti al punto chiave per capire quelle strane righe nere che  “disturbano” gli spettri stellari. Altro che disturbo! Sono proprio loro, legate ai “salti” degli elettroni nei diversi atomi, a informarci  sugli “abitanti” presenti nelle superfici stellari. La faccenda diventa sempre più affascinante. La luce è veramente una miniera di in formazioni!

Ribadiamo, ancora, un concetto rivoluzionario che ha cambiato l'aspetto dei fotoni o -ancora meglio- ha sanato l'ambiguità onda-particella. I fotoni sono vibrazioni del campo elettromagnetico e si propagano come onde. Tuttavia, ogni onda porta con sé un pacchetto di energia, che dipende dalla frequenza dell'onda. L'onda può quindi benissimo vedersi come un qualcosa di corpuscolare. D'altra parte Einstein ha dimostrato che queste onde sono in grado di colpire e spostare un elettrone. Resta solo da capire cosa siano realmente queste onde prima che si manifestino come pacchetti molto robusti. L'ultimo tassello è stato inserito dalla meccanica quantistica: le onde non sono vere onde "fisiche", ma onde di probabilità. Esse indicano solo dove il pacchetto fotone potrebbe trovarsi in un certo momento. Quando colpisce l'elettrone non c'è più bisogno di usarle dato che sappiamo dov'è il pacchetto, ma prima il pacchetto vagabondo può essere solo descritto da un'onda di probabilità. Insomma, qualcosa del genere... ma ovviamente la meccanica quantistica non si può riassumere in una frase. Noi, però, l'abbiamo già trattata in lungo e in largo e ormai non ci spaventa più di tanto.

La prossima volta affronteremo i salti quantici degli elettroni e quindi andremo anche avanti con la storia dell'atomo: le due trattazioni (modello atomico e spettroscopia) si uniscono.