Per una trattazione completa della Meccanica Quantistica, si consiglia di leggere il relativo approfondimento, in cui è stato inserito anche il presente articolo

 

Spesso e volentieri si usa un paradosso legato alla vita di tutti i giorni per descrivere l’effetto tunnel.

Immaginiamo di trovarci davanti una lastra di metallo robustissima e impossibile da perforare. Bene, se tirassimo una pallina da tennis contro la parete potremmo spendere tutta la nostra esistenza in questo esercizio fisico ma continueremmo a vedere la pallina tornare indietro dopo aver urtato la parete. L’effetto tunnel ci dice invece che esiste una possibilità concreta che la pallina, prima o poi, attraversi il muro. In realtà, enunciato in questo modo, l’effetto tunnel è molto affascinante, ma è del tutto impossibile. Dobbiamo rassegnarci e cambiare pallina e parete. La parete diventa in qualche modo una parete di energia e la pallina una particella microscopica, una di quelle che hanno comportamenti ben diversi dalla realtà di tutti i giorni.

Al Luna Park

Per avvicinarci meglio alle barriere di tipo energetico facciamo un esempio ancora più calzante che ci porta in un Luna Park, sulle montagne russe, in particolare. Sappiamo benissimo che le montagne russe si basano su un principio fondamentale della meccanica classica applicato a un percorso di sali e scendi di un vagoncino. Il principio è quello della conservazione dell’energia. Chi viaggia sulle montagne russe deve conservare la sua energia.

Le energie in gioco sono solo due: l’energia potenziale e l’energia cinetica. Le dovreste conoscere molto bene, ma è meglio richiamare brevemente il loro significato. Qualsiasi oggetto che sta sulla Terra è soggetto alla gravità del pianeta ed è costretto a cadere verso il basso a meno che qualcosa non lo tenga sollevato (pensate alla mela di Newton). Se saliamo sempre più in alto rispetto al suolo e se poi ci lanciamo in balia della forza di gravità subiremo effetti sempre più disastrosi. Se saliamo su una sedia, non succede praticamente niente, ma se ci buttiamo da un ponte sospeso la faccenda diventa ben più pericolosa. Ancora peggio se ci buttiamo da un aereo a 10000 metri di quota.

Cosa vuol dire tutto ciò? Che, a mano a mano che saliamo, ossia ci allontaniamo da Terra, acquistiamo un’energia sempre più grande, proprio quella che, una volta liberata, ci fa precipitare verso il suolo. Questa energia dipende solo e soltanto dalla massa della Terra e dall’altezza a cui siamo arrivati. Essa prende il nome di energia potenziale gravitazionale e viene descritta in pratica solo dall’altezza raggiunta (la Terra è sempre la stessa per i suoi abitanti).

Torniamo, quindi, al nostro ottovolante, quando siamo fermi sul punto più alto. In queste condizioni l’energia potenziale è massima, ossia siamo pronti per eseguire un lavoro non indifferente (un lavoro che potrebbe farci schiacciare al suolo). Fortunatamente siamo in un carrello che è tenuto attaccato alle rotaie in modo perfetto e ci evita cadute catastrofiche. Quale energia possediamo nel punto più alto? Solo e soltanto l’energia potenziale, riferita solo alla posizione occupata. Ripetiamo ancora: in quel momento, con il carrello fermo, tutta l’energia che possediamo è l’energia potenziale.

Aspettiamo ancora un attimo prima di far partire il vagoncino…

L’altro tipo di energia che conosciamo molto bene nella vita di tutti i giorni si chiama energia cinetica ed è quella legata al movimento. Quando corriamo o andiamo in macchina o in treno o quello che volete, abbiamo una certa energia che è legata alla nostra massa (più siamo pesanti e più difficile è muoversi) e alla velocità con cui ci spostiamo. Se qualcuno fosse fermo lungo la strada e ci vedesse passare alla guida di una macchina potrebbe misurare la nostra velocità e, sapendo il peso totale della macchina più passeggero, misurerebbe facilmente l’energia che ha la vettura, in quell’istante.

Bene, torniamo in cima all’ottovolante. Prima di partire ricordiamoci il principio di conservazione dell’energia. Esso dice che l’energia che ha un certo oggetto, o sistema qualsiasi, deve sempre essere la stessa. Se vi sono più energie in  gioco la loro somma deve rimanere costante. In poche parole se diminuisce una certa energia deve aumentare l’altra in modo che la somma resti sempre la stessa.

E’ ora di dare il via al nostro carrello. Via! Ci accorgiamo in fretta che l’energia cinetica sta cambiando drasticamente. All’inizio eravamo fermi e quindi la velocità era zero e, quindi, anche l’energia cinetica. Adesso stiamo precipitando a grande velocità e la nostra energia cinetica sta aumentando decisamente. La conservazione dell’energia, però, non può sbagliare. L’energia che stiamo guadagnando deve andare a scapito dell’altra energia che possedevamo all’inizio (l’unica), quella potenziale. In effetti è vero!

A mano a mano che scendiamo, l’energia potenziale diminuisce sempre di più, dato che diminuisce l’altezza dal suolo. La fisica non sbaglia mai: se in ogni istante della discesa facessimo la somma delle due energie troveremmo sempre lo stesso identico valore.

Finalmente, con lo stomaco in bocca, arriviamo in fondo alla discesa. L’energia potenziale è diventata zero (più in basso non possiamo andare), ma l’energia cinetica è altissima, anzi è l’unica che possediamo ed è esattamente uguale a quella potenziale che avevamo prima della partenza, lassù in cima alle montagne russe. Ci fermiamo? Assolutamente no! Siamo in  balia dell’energia cinetica, un’energia di movimento. Il carrello sfrutta questa energia che abbiamo accumulato in  discesa e continua a muoversi anche se il percorso è, adesso, in salita. La velocità diminuisce, ma il vagoncino continua a salire. Fino a quando?

Se non ci fossero attriti, andrebbe avanti fino a sperperare tutta l’energia cinetica. Tuttavia, mentre stiamo salendo, anche se sempre più lentamente, stiamo riguadagnando energia potenziale, dato che ci stiamo alzando rispetto al suolo. Non possiamo nemmeno dimenticare che l’energia totale deve conservarsi. Ciò comporta che quando l’energia cinetica diventa zero (ossia il vagoncino si ferma) abbiamo riguadagnato tutta l’energia potenziale che avevamo all’inizio del giro in giostra. Siamo tornati nelle condizioni iniziali, quando tutta l’energia che avevamo era quella potenziale.

La Fig. 1  mostra schematicamente quello che è successo. Scusate se ho riproposto un esempio ben conosciuto da tutti, ma per qualcuno potrebbe non essere male richiamare in modo semplificato e senza formule un classico esempio (molto divertente) di conservazione dell’energia meccanica.

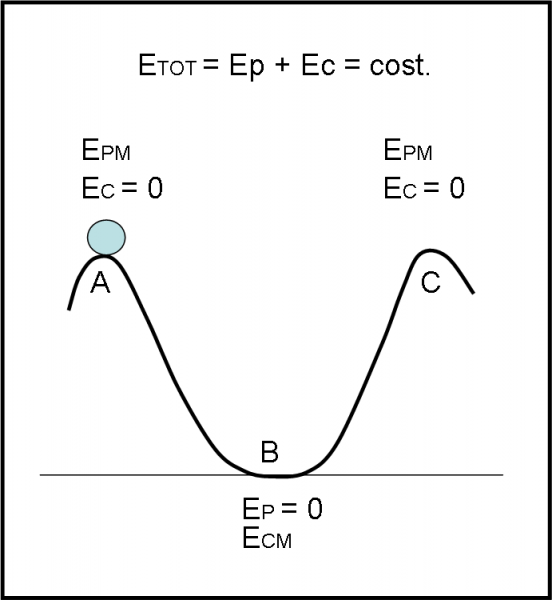
Non sarebbe, quindi, molto difficile (teoricamente) costruire un otto volante molto più complicato: l’importante è che il sali e scendi non vada mai contro questo banalissimo schema (a parte la costruzione del carrello, la tenuta delle ruote sui binari e molte altre cose legate alla sicurezza).

Il progettista che ha costruito le montagne russe della Fig. 2 è, invece, un incompetente e capisce ben poco di meccanica classica. Vi è qualche speranza che il carrello che parte da A e scende fino in B possa mai raggiungere il punto C? Assolutamente no! Quando il carrello arriva nel punto A’, ha sperperato tutta la sua energia cinetica (velocità uguale a zero) e possiede solo l’energia potenziale. Questa però, per la conservazione dell’energia, non può superare quella che aveva in A. Il carrello non può certo salire ancora perché, se lo facesse, guadagnerebbe ulteriore energia potenziale, cosa impossibile in meccanica classica. L’energia non si crea dal niente e quella che abbiamo ci dobbiamo tenere.

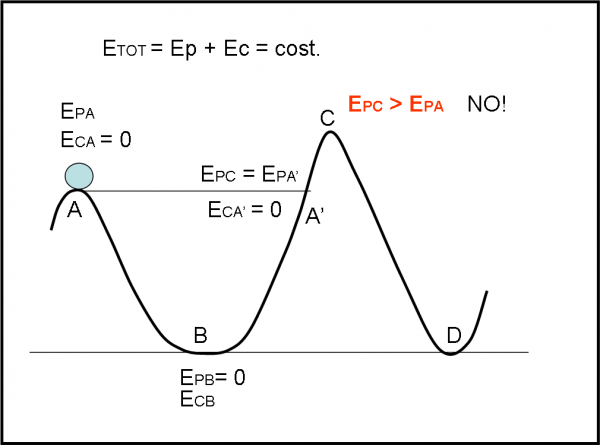
L’unica speranza per poter proseguire sarebbe la bacchetta magica di una fata o di qualche personaggio veramente speciale. Nel mondo quotidiano non esistono maghi o streghe o fate: il carrello è costretto a ricadere all’indietro verso il punto B  e tornare nuovamente in A. Una giostra poco divertente… Le cose, però, possono cambiare se il nostro otto volante diventa estremamente piccolo, talmente piccolo che possa intervenire la simpaticissima Alice (del Paese delle Meraviglie), proprio la bimba che ci ha introdotto nel mondo della Meccanica Quantistica.

Barriere energetiche

Mettiamo, allora, da parte l’otto volante, ma teniamo bene a mente che l’impossibilità di arrivare fino a C rappresenta una barriera della vita quotidiana, una barriera energetica, qualcosa di molto simile alla parete che colpivamo con la pallina da tennis sperando di passarle attraverso. Per superare la barriera o arrivare fino alla cima della giostra, in C, il problema è lo stesso: bisogna essere in grado di superare una barriera energetica, ossia riuscire ad avere in regalo dell’energia che la meccanica classica non può assolutamente darci.

Abbiamo cambiato scenario, siamo diventati piccolissimi e riusciamo a vedere gli atomi. Che belli, con quel loro nucleo e tutti quegli elettroni che girano attorno, al pari di api attorno a un alveare. In realtà, assomigliano molto a delle api. Sembra di vederli. Esprimiamoci meglio. Siamo sicuri che ci siano, ma non è assolutamente facile vederli. Dobbiamo accettare la verità: sappiamo che gli elettroni ci sono, ma dobbiamo ammettere di non vederne nemmeno uno. Sicuramente vanno troppo veloci. Se ci fissiamo su una certa posizione, dove sappiamo che l’elettrone deve sicuramente esistere, non lo vediamo perché non sappiamo assolutamente la traiettoria che sta seguendo, ossia, parlando seriamente, non conosciamo la sua quantità di moto. Se invece riusciamo a calcolare esattamente quest’ultima quantità, perdiamo completamente la possibilità di stabilirne la posizione.

Bene, è inutile proseguire, sapete bene di cosa parlo: di uno dei principi fondamentali del mondo di Alice, ossia il Principio di Indeterminazione di Heisenberg, che ci dice che non si possono conoscere accuratamente la velocità e la posizione di una particella. Gira e rigira questo principio è sempre pronto a romperci le scatole. Lo ha fatto nell’esperimento delle due fenditure, lo fa nella definizione del modello atomico attraverso gli orbitali e continua a farlo in mille altre situazioni.

Per chi non fosse già amico intimo del mondo di Alice, faccio un esempio molto intuitivo del principio di Heisenberg, uno dei capisaldi di tutta la MQ e non solo (ci servirà ancora molto). Supponiamo di avere un segnale che varia nel tempo, proprio come un'onda, e che si voglia sapere, in un certo istante, la frequenza esatta del segnale. Purtroppo, è  impossibile! Infatti, per poter determinare la frequenza, è necessario seguire il segnale per un certo intervallo di tempo, almeno coprire un periodo dell’oscillazione. Facendo così, però, si perde automaticamente la precisione dell’istante in cui si ottiene l’informazione. Insomma, o si ha l’istante preciso o si ha la frequenza. Non si possono avere entrambi… Lo stesso concetto vale per la quantità di moto (o velocità) e la posizione o per il tempo e l’energia.

Esprimiamolo attraverso una semplice formuletta:

dx dq ≥ h/4π

dx è l’errore commesso sulla posizione e dq quello commesso sulla quantità di moto. Il loro prodotto non può essere inferiore a una certa costante che contiene nientedimeno che la costante h di Planck, che ormai conosciamo benissimo. Se un errore diventa piccolissimo, l’altro è costretto a crescere di molto.

Lasciamo da parte, per un attimo, il nostro sciame di api che gira attorno al suo alveare e pensiamo a quell’atomo che ci si para d’avanti. Non vediamo un vero e proprio muro e nemmeno un otto volante, però una barriera c’è di certo. Essa è quella che non permette a cariche di segno uguale di andarsene per strade opposte. Le api  “positive” che stanno all’interno dell’alveare vorrebbero allontanarsi tra loro, ma l’interazione nucleare forte lo vieta e le costringe a restare in quel "buco" che sembra senza uscita. Analogamente, gli elettroni sotto l’azione dell’interazione elettromagnetica, vorrebbero entrare, attratti dalle api positive, e invece sono tenuti a distanza. Che strano alveare è l’atomo! Le due forze, nucleare forte ed elettromagnetica, sembrano lottare una contro l’altra e creare barriere insuperabili.

Siamo proprio nelle stesse condizione della pallina da tennis che sbatte contro al muro o -ancora meglio- nelle condizione del carrello dell’otto volante che vorrebbe salire fino a C. Per superare una barriera energetica insuperabile è necessaria un’energia che proviene da qualche personaggio da fiaba.

Scavare un tunnel nell’otto volante

Ritorniamo alla Fig. 2 dell’ottovolante e vediamola a livello microscopico. Abbiamo delle particelle che stanno nel buco nei pressi di B e delle altre particelle che, invece, se ne stanno in D. Quelle in B vorrebbero salire fino a C e poi cadere verso D. Quelle in D vorrebbero salire fino in C per scendere in B e, poi, andarsene ognuna lontana dalle altre. La cosa migliore per accontentare entrambi i gruppi di particelle sarebbe quello di scavare un tunnel attraverso la “montagna” che ha come cima C. Forse qualche nostro ex ministro penserebbe anche di riuscirci, attraverso l’incompetenza, ma la MQ lo fa per davvero…

La spiegazione di tutto sta, in pratica, nelle definizione di “particella” che non è né onda né corpuscolo, ma viene ben  rappresentata da una funzione d’onda probabilistica, come abbiamo visto, ad esempio, nella QED e nell’introduzione alla MQ, ma anche in tante altre occasioni. Ciò vuol dire che la reale posizione di una particella è legata alla probabilità che essa ha di trovarsi in un certo punto. In parole povere, potremmo dire che la posizione di una particella che sta in uno dei due buchi descritti prima (B e D) può anche avere una possibilità non nulla di trovarsi  al di là della montagna. In fondo, anche quella posizione così assurda può avverarsi.

Ciò si può tradurre visivamente nella Fig. 3. La particella descritta dalla sua onda probabilistica si avvicina alla barriera teoricamente impenetrabile. Ebbene se la barriera energetica non è troppo spessa, l’onda riesce a proseguire attraverso di essa, diminuendo la sua ampiezza, e si ritrova, pur estremamente ridotta, al di là del muro. Il fatto che abbia ridotto la sua ampiezza vuol solo dire che è diminuita di molto la probabilità di eseguire questo esercizio, del tutto magico per la nostra vita quotidiana.

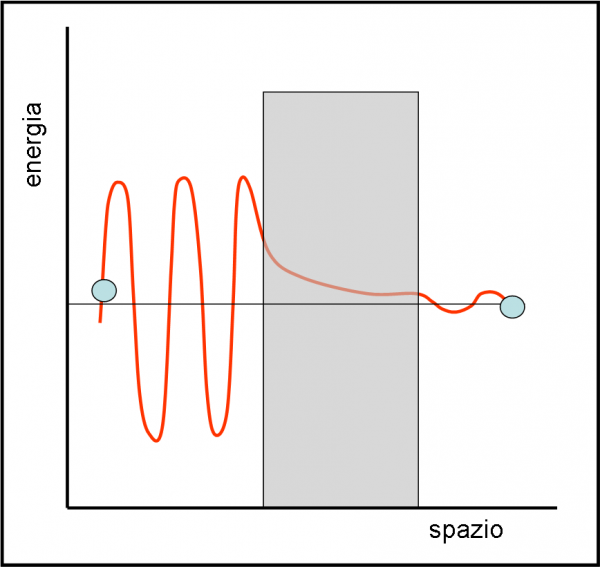
Se non amiamo troppo le onde e le funzioni d’onda, espresse con formule sicuramente non semplici, possiamo spiegare la situazione riprendendo il principio d’indeterminazione. Se conosciamo sempre meglio la posizione di una particella (vicinissima alla parete invalicabile) siamo costretti a non conoscere la sua direzione di movimento o la sua velocità e questa può anche averla portata al di là del muro.

E’ ancora più evidente la soluzione se si considera il principio d’indeterminazione quando coinvolge il tempo e l’energia. La formula è praticamente la stessa:

dE dt > h/4π

Se il tempo si riduce quasi a zero, l’energia può assumete valori del tutto inaspettati anche molto grandi. In particolare, l’energia può superare la barriera che teoricamente non potrebbe superare. Questa situazione è analoga a quella che ci dice che in tempi estremamente corti si può anche creare energia dal nulla. L’importante è che tutto torni alla situazione precedente in una frazione infinitesima di tempo. Se ci pensate bene, questo è quanto abbiamo detto relativamente alla creazione di energia nel vuoto quantico… Ma non allarghiamo tropo il discorso.

Una magia usata tutti i giorni

Sembra di parlare di pura teoria e, invece, le stelle  non riuscirebbero  a vivere senza questo effetto (loro hanno tanti atomi…). In particolare, non riuscirebbe a superare la forza nucleare forte che tiene unito l’atomo. Senza l’effetto tunnel non ci sarebbe, perciò, decadimento radioattivo, il fenomeno che fa scappare particelle dall’interno del nucleo verso l’esterno… ma non riuscirebbero nemmeno a unire due nuclei atomici e quindi  a ottenere la fusione nucleare o la cattura degli elettroni da parte del nucleo. Non ci sarebbero nemmeno i trasporti di elettroni che ci permettono di costruire i microscopi a effetto tunnel e cento altre applicazione che stanno evolvendo dalla tecnologia dei computer fino alla medicina più sofisticata.

Insomma, le stelle e molte altre cose non potrebbero esistere…

Non ho voluto inserire formule (non difficilissime a un primo livello, ma che diventano mostruose se si introduce la funzione d’onda). Tuttavia, con quanto già sappiamo sulla MQ, direi che l’effetto può essere compreso perfettamente a livello concettuale.

Riassumendo:

L'Effetto Tunnel è la capacità che possiedono le particelle quantistiche di attraversare una barriera energetica più alta dell'energia che avrebbero a disposizione!

 

Volete scoprire come osservare un effetto tunnel "fatto in casa"? Ne parliamo QUI