Vediamo prima cosa succede al gas e alla povere che compone un disco di accrescimento che ruota attorno a un buco nero galattico. La struttura è abbastanza ben conosciuta: nelle parti più esterne vi è l’anello di polvere, mentre nella parte interna vi è il gas. Il gas si scalda sempre di più ed emette nell’ultravioletto. Questa luce arriva a noi a un certo istante t_UV.

Ovviamente non è un luce continua, ma subisce sbalzi di luminosità, ossia descrive una certa curva di luce. La luce emessa da questo gas caldissimo se ne va in tutte le direzioni e non solo verso di noi. Ve ne è un parte che arriva fino al disco di polvere e lo eccita, costringendolo ad emettere nell’infrarosso. Bene, noi siamo in grado di rivelare anche questa radiazione. Essa descrive una curva di luce che in qualche modo rispecchia quella ottenuta dal gas che l’ha originata.

La luce va veloce, però ci mette  del tempo per passare dal punto in cui si è originata fino alla nube di polvere che emette nell’infrarosso al tempo t_IR. In parole, molto semplificate, vi è un ritardo tra le variazioni viste nella curva UV e quelle corrispondenti della curva IR. Questo ritardo è dato proprio da Δt = t_IR - t_UV. Una misura di intervallo di tempo che può essere di giorni o di mesi a seconda dello spessore del disco di accrescimento e, quindi, anche della massa del buco nero. Sì una cosa interessantissima di per sé, ma che può avere ricadute ancora più interessanti.

Noi sappiamo benissimo il valore della velocità della luce e, quindi, possiamo anche calcolare lo  spazio  percorso dalla luce nel tempo Δt. Concludendo, l’analisi delle due curve di luce (fatti i dovuti aggiustamenti e le dovute medie, ecc., ecc.) permette di determinare la distanza reale tra la parte più interna del disco di accrescimento e l'anello di polvere più esterno. E le cose diventano molto stimolanti...

Sappiamo bene come si misura la distanza di una stella attraverso la parallasse trigonometrica. La riportiamo in Fig. 1, per i meno esperti…

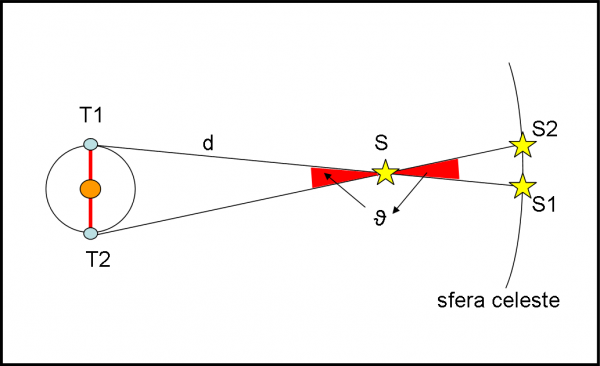
La stella si muove nel cielo durante un anno, descrivendo una piccola ellisse, a causa del moto della Terra attorno al Sole. Si sposta apparentemente da S₁ a S₂ in sei mesi. Da terra possiamo misurare la dimensione angolare di questa piccola ellisse che altro non  é  che quella dell’orbita della Terra vista dalla stella (angolo rosso). Noi, però, conosciamo esattamente la dimensione reale dell’orbita terrestre e, di conseguenza, la misura dell’angolo di spostamento della stella permette di ricavare la distanza d della stella, attraverso il triangolo  T₁T₂S. E’ un metodo ben conosciuto che si basa su una figura semplicissima, già utilizzata teoricamente dagli scienziati greci (peccato che loro non riuscivano a misurare la piccola ellisse delle stelle, ma l’avevano prevista!).

Il metodo, applicato al buco nero galattico, è molto simile concettualmente e viene riportato in Fig. 2.

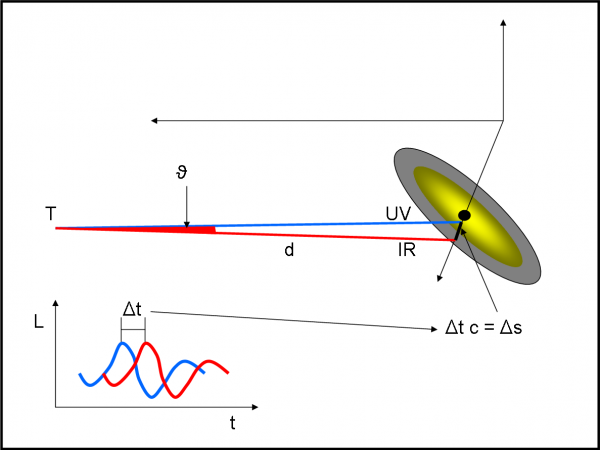
La luce ultravioletta del disco gassoso interno, molto caldo, arriva direttamente sulla Terra attraverso la linea blu. Osservandola in funzione del tempo vediamo che descrive la curva di luce blu nel diagramma (t,L), in basso a sinistra. La stessa luce, partita nello stesso momento, arriva, però, fino al disco esterno di polvere “grigio” e lo eccita facendolo emettere nell’infrarosso. Parte di questa luce infrarossa arriva sulla Terra con un certo ritardo, dovuto al tempo impiegato dalla luce per andare dalla parte più vicina al buco nero fino alla parte più esterna (segmento nero).

Anche questa luce IR descrive una curva di luce che rispecchia molto bene quella emessa dalla luce UV. Sarà simile all’altra, ma spostata rispetto al tempo. La differenza Δt ci regala subito la distanza reale tra zona vicina al buco nero e disco di polvere, attraverso la relazione Δs = c Δt (la velocità della luce c è pur sempre uguale allo spazio diviso il tempo…).

Cosa ci manca per potere applicare lo stesso metodo della parallasse trigonometrica al buco nero e al suo disco di accrescimento? L’angolo, visto da terra, tra la zona luminosissima ultravioletta del disco e la zona esterna polverosa e infrarossa. A questo c’ha pensato il telescopio "doppio" Keck da 10 metri alle Hawaii che, combinando i due strumenti con l’interferometria, è riuscito a comportarsi come un telescopio da 85 metri, per quanto riguarda il suo potere risolutivo. Siamo intorno ai milionesimi di grado… mica bruscolini!

Il solito triangolo ha permesso di misurare la distanza d della galassia in oggetto.

Parliamo un po’ di lei. Si tratta di NGC 4151, più nota come l’Occhio di Sauron, legato alla saga del Signore degli Anelli (io non me ne intendo…). In ogni modo proprio un anello ha risolto molti problemi legati alla galassia. La sua distanza era molto incerta e i normali metodi non riuscivano a fare di più… Poteva, infatti, essere di 4 come di 29 megaparsec. Un errore niente male! Con il nuovo metodo si è ottenuto un valore di 19 +/- 2 megaparsec, un bel passo in avanti.

A parte i risvolti fisici legati alla struttura del disco e alla massa del buco nero, quello applicato all’Occhio di Sauron potrebbe essere un nuovo metodo, estremamente accurato, per la determinazione di galassie relativamente vicine. Tra l’altro potrebbe “testare” valori ottenuti con altri metodi e la stessa legge di Hubble.

L’ho sempre detto che le Hawaii sono veramente speciali!

Articolo originale QUI.