Categorie: Sistemi multipli
Tags: baricentro binarie a contatto giganti marea sincronizzazione periodi vagabonde blu
Scritto da: Vincenzo Zappalà
Commenti:17
Uno più uno fa uno *
Non sto parlando di meccanica quantistica e non sono nemmeno impazzito. Può capitare che nell’Universo a volte valga la somma che ho appena enunciata. Se ci pensate bene è una cosa che abbiamo visto spesso, ma quella a cui voglio riferirmi oggi è relativa a due stelle veramente fuori dal comune.
Prima di passare all’argomento di questa “news”, fatemi dire che capita sempre più sovente che dopo un articolo relativo a un certo argomento, sbuchi fuori subito una notizia che si rifà perfettamente a quello che abbiamo appena detto. Si è parlato di marea e di sincronizzazione orbitale… ed ecco che L’Universo ci vuol far sapere che conosce molto bene quello di cui stiamo parlando. E poi si dice che non vi è una rete conoscitiva che collega tutto ciò che esiste… Come non pensare all’Universo come a un enorme cervello pensante che sa tutto di tutte le sue componenti, noi compresi? In fondo le particelle “entangled” (di cui si parla nelle lezioni di Meccanica Quantistica) lo hanno già dimostrato…
A parte gli scherzi (?), abbiamo appena parlato di marea e due veri e propri mostri celesti ci dimostrano che la sincronizzazione perfetta dei periodi la applicano molto bene anche loro. Contemporaneamente, dimostrano ancora una volta che “uno più uno può fare uno o stare per fare uno”. Beh, in realtà, non possiamo stupirci più di tanto. Quante volte abbiamo parlato di galassie che si uniscono per formarne una sola? Una più una uguale a una. E che dire dei buchi neri galattici che si uniscono dopo avere eseguito balletti in grado di produrre le tanto agognate onde gravitazionali? (NEWS!! Rilevate le onde gravitazionali)
Ma anche le stelle ci hanno abituato a questo tipo di “somma”. Vi ricordate le vagabonde blu degli ammassi globulari? Stelle che, data la loro massa, dovrebbero ormai essere sulla via del tramonto e che, invece, appaiono come giganti ancora in piena forma, lungo la linea della sequenza principale (QUI ). Una vera e propria fontana della giovinezza.
Vale anche la pena rispondere un po’ meglio alla domanda formulata da Davide1334 sulla classificazione dei sistemi binari. Una domanda tutt’altro che banale alla quale, probabilmente, nessuno ha ancora pensato di dare una risposta perfettamente definita.
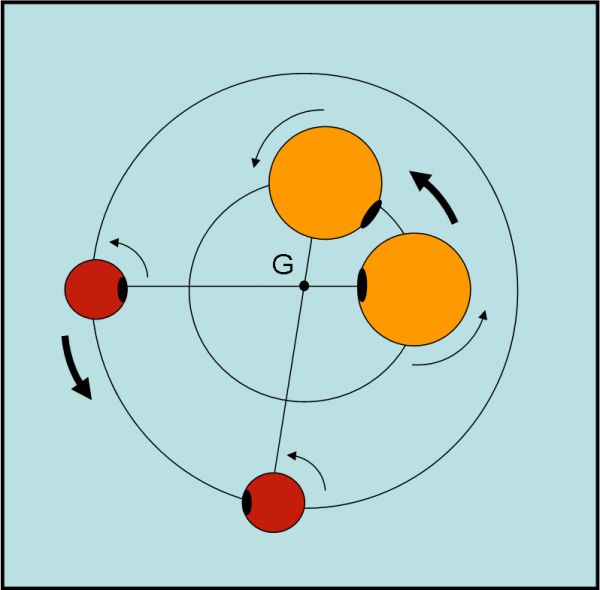
Quando si parla di stelle binarie non si va molto per il sottile. L’importante è che ci siano due stelle che rivolvano attorno a un comune baricentro (QUI viene spiegato cos’è il baricentro di un sistema), eseguendo la danza che si vede nella Fig. 1. Una delle due potrebbe anche essere molto più piccola e far sì che il baricentro cada all’interno della più grande. Non è facile che questo capiti, ma teoricamente non vi sono problemi.
Nel Sistema Solare vige, invece, una specie di “razzismo”. Non si possono mischiare stelle con pianeti. D’altra parte, se così fosse, qualsiasi pezzo di roccia e/o ghiaccio che girasse attorno al Sole formerebbe con lui un sistema doppio… Si parla, allora, di possibili pianeti doppi, dove vengono confrontati pianeta e satellite. Si va a vedere dove finisce il baricentro della coppia: se è fuori dal pianeta, allora il sistema diventa un pianeta doppio. Non capita sovente, se non per Plutone e Caronte (i cui satelliti hanno vita dura, come potete leggere QUI) e qualche asteroide e, facilmente, per altri KBO.
Avremmo finito con le definizioni, se non ci avesse pensato Davide. E se il pianeta doppio si è anche sincronizzato? In realtà, un pianeta doppio comporta masse abbastanza simili ed è facile che i tre periodi abbiano deciso di diventare tutti uguali. Tuttavia, nel caso non lo fossero potremmo coniare una definizione “davidiana”: un pianeta doppio sincronizzato lo potremmo chiamare doppiamente doppio! Stiamo, ovviamente, scherzando, dato che in fondo poco importa la definizione, bensì il processo fisico che sta agendo e le condizioni raggiunte.
Le stelle, ad esempio, che abbiamo visto essere comunque binarie quando fanno il girotondo tra di loro, si dividono in tre categorie molto importanti, che si riferiscono alla situazione raggiunta e che comportano una fenomenologia alquanto differente. Le prime sono le cosiddette binarie staccate. Sono costrette a seguire le leggi Keplero, ma hanno ben pochi scambi diretti: ognuna va per la sua strada e la distanza che le separa è decisamente superiore alla grandezza degli astri. Vi sono, poi, le binarie semistaccate, in cui una delle due riempie completamente il lobo di Roche (il lobo, non il limite!). E’ questa la condizione ideale per la “trasfusione” di materia dalla più grande alla più piccola attraverso il punto lagrangiano L1.
Riguardando la Fig. 1, possiamo ancora dire, però, che anche se sono vicine e se vi è uno scambio di materiale, non è detto che le due stelle non continuino a ruotare ciascuna a modo suo. Molti fattori devono essere tenuti in conto. Tuttavia, possiamo immaginare, soprattutto per binarie staccate, che le macchie stellari, ad esempio, seguano la rotazione della loro stella e che si guardino tra di loro solo di tanto in tanto. Non confondiamo, quindi il filo diretto che lega la posizione delle due stelle attraverso il baricentro (ognuna deve stare sempre alla stessa distanza da questo punto come in una perfetta altalena, nel caso di orbite circolari),con il fatto che vi sia realmente una “barra” che le tenga bloccate sempre nella stessa posizione reciproca, ossia che continuino a guardarsi in faccia (Fig. 2).
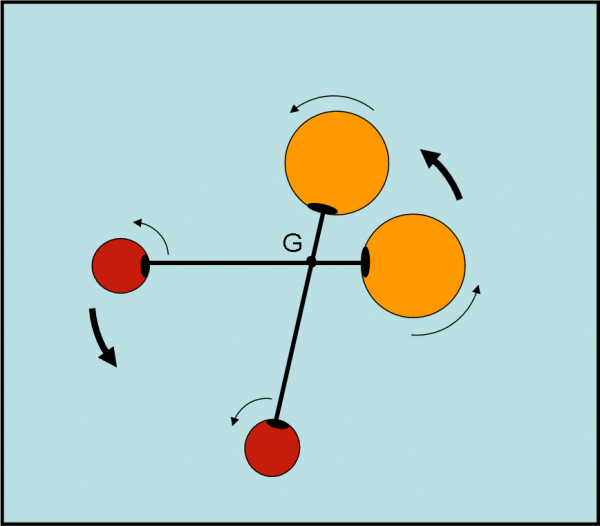
Nell’ultimo caso le rispettive macchie sarebbero sempre una di fronte all’altra, in modo simile a quello che fanno Plutone e Caronte. Siamo in queste condizioni sicuramente quando i sistemi binari sono veramente a contatto. In parole scientifiche, quando entrambe le stelle riempiono i loro lobi di Roche.
I lobi di Roche implicano, normalmente, un’altra condizione. La stella che riesce a riempirlo è un oggetto uscito dalla sequenza principale che si è gonfiato nella vana ricerca di ripristinare la situazione di equilibrio nel suo motore “atomico”. A maggior ragione dovrebbero esserlo due stelle che riempiono entrambe i loro lobi di Roche. E, invece, qualche volta non succede ed eccoci, finalmente, alla nostra news (che fatica…).
Il sistema doppio osservato è noto da una decina d’anni, ma è stato studiato continuamente anche con l’aiuto di “veri” astrofili (meglio dire “astronomi dilettanti”), fino a ottenere, oggi, una visione perfettamente chiara di cosa rappresenta. E’ composto da due stelle entrambe di sequenza, giovanissime, di un paio di milioni di anni, ma talmente vicine da riempire entrambe i loro lobi di Roche. Una coppia nata già a contatto, come due sorelle siamesi. Hanno iniziato a scambiarsi materia fin dall’inizio, anche se entrambe ne hanno a sufficienza. Pensate che le loro masse sono di 32 e 38 masse solari rispettivamente. Due giganti “bambine” che risplendono di luce azzurra.
Ovviamente la marea ha fatto in fretta a sincronizzare tutto ciò che si poteva sincronizzare e le due stelle ruotano come una cosa sola, in modo simile a quanto disegnato nella Fig. 3. Praticamente vi è una sola atmosfera che le inviluppa tutte e due.

Diamo qualche numero abbastanza impressionante. Il periodo di rivoluzione delle due stelle che, però, può essere anche inteso come la rotazione di questa specie di “nocciolina americana”, è di solo 1.2 giorni terrestri. Il che significa che anche le singole stelle ruotano a questa velocità intorno al loro asse che è poi lo stesso per entrambe e anche per l’orbita. Tuttavia, fa impressione pensare che il Sole, molto più piccolo, ruota in 26 giorni e questi “mostri” in poco più di un giorno. Il che comporta una velocità superficiale di oltre un milione di chilometri allora.
Ah… dimenticavo , la coppia di gigantesche sorelle si chiama MY Cam.
Come già detto, le stelle sono già nate in queste condizioni, ma con l’età tenderanno a ingrassare un pochino (con quelle masse non si vive molto) e faranno in fretta a toccarsi veramente fino a compenetrarsi (come quelle descritte nella 2° sezione di questo articolo). Non si sa ancora come questa unione avvenga, dato che il momento fatidico non è mai stato visto in diretta, ma potrebbe essere sia molto scenografico che abbastanza tranquillo.
Uno più uno uguale a uno, come dicevamo all’inizio. Tuttavia, la somma vale solo per il numero di oggetti coinvolti, dato che la massa finale della stella unica sarà la somma delle masse, circa 70 masse solari. Veramente una fuoriclasse.
Si pensa, tra l’altro, che le stelle con masse spropositate siano proprio nate in questo modo, da due stelle vicinissime e di massa comparabile.
Qualcosa di più tecnico, per concludere. Il sistema è stato studiato sia attraverso la fotometria, ottenendo una curva di luce uguale a una sinusoide quasi perfetta (le eclissi sono continue e praticamente uguali), sia attraverso la spettroscopia. I risultati sono mostrati in Fig. 4 e 5. La prima mostra la variazione di luminosità rispetto alla fase (che è il tempo diviso al periodo) e la seconda la velocità di avvicinamento e allontanamento di entrambe le stelle. Ovviamente quando una sta allontanandosi alla massima velocità, l’altra si avvicina e viceversa.
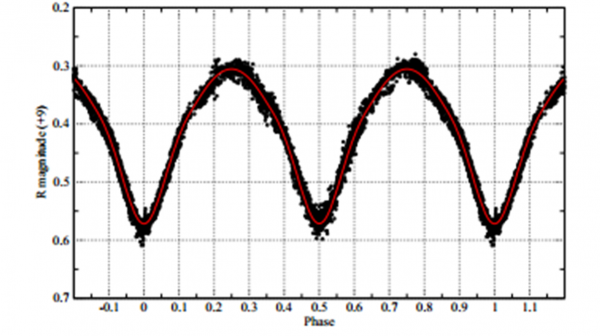

Il lavoro originario si trova QUI






17 commenti
Queste stelle ci stupiscono sempre.
Peccato che, per quanto "poco tempo" servirà affinché si uniscano, in tempi umani potrebbe voler dire decisamente "troppo tempo".
Allora Enzo, mi sono divertito a fare qualche calcolo. Vediamo se ho scritto bestialità.
Ipotesi:
1. Due masse sferiche a contatto nel punto di tangenza (per semplicità si considera il sistema in equilibrio statico)
2. Velocità superficiale V pari a 1.000.000 km/h = 277.778 m/s
3. Velocità angolare di rotazione ω pari a 360°/29h = 0,00006 rad/s
4. R sia la distanza tra il centro di massa (per semplicità posto nel centro geometrico del sistema) e la superficie estrema di una delle due masse (considerate delle stesse dimensioni per semplicità).
Essendo: V = ω*R, si ottiene che il diametro R di ciascuna massa stellare è di circa 4,6 milioni di km.
Consideriamo che il diametro del Sole è circa 1,4 milioni di km.
Ora proviamo a valutare la forza centrifuga Fc a cui è sottoposto un elemento di massa m che si trovi a distanza R dal centro di massa. Fc = m* ω^2*R.
D’altra parte la forza di gravità Fg a cui è sottopoto lo stesso elemento di massa vale: Fg = G*M*m/R^2
Il rapporto Fc/Fg vale dunque: ω^2*R^3/(G*M).
La massa M è la somma delle due masse stellari, per cui M = 70 masse solari. Tale massa è supposta concentrata nel centro di massa.
Essendo:
ω^2 = 3,6*10^-9 (rad/s)^2
R^3 = 9,73*10^28 m^3
G = 6,7*10^-11 m^3/(kg*s^2)
M = 2*10^30 kg
Se ho svolto i calcoli correttamente si dovrebbe ottenere:
Fc/Fg = 2,6. Quindi l’elemento di massa sarebbe sbalzato fuori dalla comune.
Pur trattandosi di un esercizio puramente teorico, è' corretto il ragionamento ed i conseguenti calcoli ?
caro Alvy,
mi compiaccio per il tuo esercizio. Non ho fatto i calcoli, ma mi "puzza" un po' il fatto che tu stia considerando un po' le stelle come separate e un po' come un sistema unico. Il centro di massa è quello delle due, ma poi calcoli le forze per ciascuna stella o sbaglio? Bisognerebbe usare il diagramma che porta ai lobi di Roche con le superfici equipotenziali (quello che indica i vari punti lagrangiani...) per vedere bene come giocano le forze in un sistema doppio rotante. Temo che sia troppo semplificato...
caro Alvy,
puoi dare un'occhiata a questo...
http://astrofisica.altervista.org/doku.php?id=c11:sistemi_binari_stretti
Ho considerato la massa totale (70 masse solari) concentrata in un punto (il centro di massa) ed un elementino di massa trascurabile posto a distanza R dal centro di massa (R è il diametro di una delle due stelle).
La forza gravitazionale agente sull'elemento m l'ho addebitata alla massa COMPLESSIVA M1+M2=70 masse solari. Per la forza centrifuga mi sono basato sulla velocità angolare che hai riportato nell'articolo, valore riferito allo strato più esterno di una delle due stelle (che ho considerato uguali).
Che la mia rappresentazione sia semplificata non c'è dubbio, ma non capisco dove ho sbagliato concettualmente. Comunque leggo il tuo link.
caro Alvy,
il fatto è che tu hai trascurato il fatto che le masse in gioco sono due... Il tuo caso è quello di una singola massa rotante...
Forse ho capito.
Trattandosi di due masse molto vicine all'elementino "sonda" non posso semplificare il problema concentrandole nel comune centro di massa, cosa che avrei potuto fare nel caso in cui le due masse fossero state sufficientemente distanti (ad esempio, problema dei tre corpi con due oggetti molto vicini tra loro e piuttosto lontani dal terzo). Corretto?
Bene bene, grazie al tuo link potrò entrare meglio nel dettaglio. Grazie.
Eh sì, Alvy... il problema si complica e proprio lo studio delle superfici equipotenziali in cui si tiene conto sia della rotazione che della reciproca gravità porta alla figura che trovi nel link. E' un classico per capire come si muovono i punti del sistema. I punti lagrangiani escono come punti di soluzione particolare che rimangono solidali... Non è proprio banale, comunque... Va oltre al blog... e non riuscirei a semplificarlo più di tanto, se non in modo qualitativo, come ho fatto nei vari libri... costruendolo approssimativamente. Buon divertimento!!!!
Non me lo devi semplificare Enzo. A me non piace vincere facile
Il sale del blog, almeno per me, sono - oltre ai tuoi articoli che, ovviamente, costituiscono la base di discussione - proprio questi approfondimenti. Grazie.
Caro Enzo, ho letto l'approfondimento sui sistemi binari stretti che mi hai consigliato.
La spiegazione è piuttosto chiara e definisce molto bene il senso dei lobi di Roche e dei punti Lagrangiani che peraltro hai già trattato nei tuoi articoli.
Ho svolto di nuovo i calcoli basandomi sul potenziale anzichè sulla forza, ed ho ottenuto:
Pc (potenziale centrifugo) = 38*10^9 J/kg
Pg (potenziale gravitazionale) = 41*10^11 J/kg
Il punto di calcolo è sempre sulla superficie di una delle due stelle, dal lato opposto al centro di massa.
Si ottiene che il potenziale gravitazionale è circa 100 volte maggiore di quello centrifugo e quindi il punto materiale rimane ben saldo al suo posto!
N.B.: nei miei calcoli c'è un errore (ho portato in conto un valore della massa totale molto inferiore a quello effettivo), che modifica sostanzialmente la conclusione: anche nel caso (errato) della mia semplificazione il punto materiale rimarrebbe al suo posto. Sarebbe però molto diverso il rapporto tra i potenziali.
Bene, è stato un utile esercizio ed in più ho imparato a trattare con .... i guanti i sistemi binari stretti. Grazie ancora.
ottimo Alvy...

so già a chi passare il blog quando non ce la farò più... (e non sto scherzando). Tra Paolo, tu, SMA e spero molti altri riuscirete a mandarlo avanti meglio di me. Sarebbe bellissimo non vederlo sparire insieme a me...
Va beh... non pensiamo alle cose tristi e domani vi mando il mio regalino di Natale (quantistico ovviamente...)
Tra parentesi, Alvy (e lo dico sul serio), perché non provi -tempo permettendo- a scrivere passo a passo quello che hai calcolato? Sarebbe bellissimo che tu pubblicassi un esercizio di questo tipo. Ovviamente, darei un'occhiata, ma sono convinto che andrebbe tutto bene. Il blog diventerebbe ancora più interattivo (nel senso "giusto") e si inizierebbe il (lungo, spero) percorso verso il passaggio delle consegne.
Pensaci sopra e avrai tutto il mio appoggio. Ogni tanto stuzzico verso problemini da risolvere. Beh... questo è un bel problemone per la maggior parte dei lettori!!!!
Ma come, da somarello a tuo sostituto? Manca il senso della misura.... Dai Enzone, scherzo!!
Comunque la tua proposta mi stuzzica alquanto (parlo dell'esercizio non della tua sostituzione!!) . Bene, vedrò cosa riuscirò a tirare fuori, ma il tuo controllo è doveroso; non vorrei far propalare notizie infondate.
In quanto al ruolo di responsabile del blog, caro Enzo, un conto è muoversi nei binari da te tracciati essendo sottoposti la tua continua supervisione, altra cosa è andare a ruota libera. Temo che la forza centrifuga ci sbatterebbe (me, Paolo e SMA) ai confini dell'universo conosciuto...
beh, Alvy, spero di durare ancora un po'... giusto il tempo perché diventiate perfetti!
Ciao Enzo.
 io la vedo triste x questo blog senza di te....
io la vedo triste x questo blog senza di te.... .
.


Che succede Vincenzo gia scrivi il testamento.....
Spero solo che i ragazzi da te indicati oltre alla preparazione scientifica siano capaci di interagire con gli altri come sai fare tu
Spero davvero di sbagliarmi
Bisogna che i tuoi eredi imparino a interagire e non solo pensare solo al proprio aspetto come pavoni che scorrazzano nell aia .
Senza questa dote secondo me innata e che tu Enzo hai la fortuna di avere credo di non riuscire ad intravedere un futuro radioso per il blog e se vivro a lungo lo vedro decadere
Scusa se uso parole crude ma come gia sai io cerco di dire sempre quel che penso.
Naturalmente e con Gioia spero di essere smentito per il bene di chi AMA la scienza.
Dai Foscoul,
non dire così... se siete qui e continuate a leggere e a fare domande e commenti è proprio perché siamo perfettamente in sintonia. I misteri insolvibili e le spiegazioni fatte solo per mettersi in mostra (ed è meglio se sono poco comprensibili) non fanno parte della nostra... cultura scientifica ed etica.
Portare piu persone possibile sullo stesso livello .....
Bella sfida.... Interagire tra di noi cercando sempre la chiarezza e se possibile la semplicita che giovamento ne trarrei ad assistere allo sfoggio di cultura del sapientino di turno che me ne faccio di tutto cio che beneficio ne trarrei...
Bla bla bla tante parole che non portano a nulla.....
non riesco a capirti Foscoul...
ho dato spesso esercizi da risolvere. Mi sembra un modo molto buono per mettersi alla prova. Perché non vedere come si riesce a esporre un'idea, un calcolo o cose del genere? Ovviamente, sarebbe un "una tantum", ma tutto serve a entrare sempre più nel mondo dell'Universo. Anche all'Università si svolgono le prove e riuscirci è solo un mezzo per migliorarsi e non certo per sentirsi più sapienti di chi insegna.
Devo rifletterci un po' sopra...