Forse non mi sarebbe mai venuto in mente di affrontare questo problemino elementare, se non fosse apparso un articolo proprio su questo “mistero”. No, non è un mistero e con un disegno banale si capisce benissimo il fenomeno. Volevo quasi porlo come “domanda” a voi… Anzi, chi vuole può provare a risolverlo. Leggendo gli articoli che avevo scritto sui fenomeni mutui dei satelliti medicei ci si può arrivare facilmente. Sicuramente, se i greci avessero avuto un binocolo, non avrebbero avuto problemi a spiegare lo “strano”, ma semplicissimo evento.

L’ apparentemente  complicato e imprevedibile "mistero" riguarda il fatto che da uno stesso punto della superficie di Giove si possono vedere, teoricamente, ben tre eclissi di Sole, nello stesso giorno (gioviano), causate dallo stesso satellite.

Nessun mistero, nessuna difficoltà e nessun programma a scatola chiusa: basta, come sempre, carta e matita. Oltretutto, il fenomeno sarebbe già stato risolto dagli antichi greci se solo fossero riusciti a vedere a occhio nudo le eclissi dei satelliti di Giove. Non per niente, avevano già pensato alla parallasse stellare e si erano già inventati gli epicicli per spiegare i moti apparenti dei pianeti in una sistema geocentrico. Problema quest’ultimo di assai più difficile soluzione rispetto alle tre eclissi giornaliere di uno stesso satellite su Giove.

Vorrei percorrere tutta la strada che porta dalla parallasse stellare al moto apparente dei pianeti e alla sua applicazione alle eclissi dei satelliti medicei. Sono tre risvolti della stessa identica medaglia. Per chi ha già seguito i miei articoli sulle occultazioni, i transiti e i fenomeni mutui dei satelliti di Giove risulta addirittura elementare, tuttavia vale la pena fare quattro o cinque disegni molto piacevoli e divertenti. Cominciamo, però, con il risolvere il terribile “mistero” delle tre eclissi: un vero gioco da bambini!

Poi, magari, ripartiremo da capo, parlando anche un po’ di greci e di epicicli…

L’importante, per far riuscire il gioco di prestigio, è che la velocità orbitale del satellite sia leggermente più bassa di quella di rotazione di Giove.

A questo punto, potreste anche riuscire a risolvere il problem da soli. Non solo, ma anche vedere cosa succede se la velocità di rivoluzione del satellite è maggiore di quella di rotazione di Giove oppure nettamente più bassa. Mettetevi nelle condizioni più semplici possibili e guardate come si muove un punto P su Giove e come si muove contemporaneamente il satellite.

Per semplificare la trattazione, dato che stiamo pur sempre parlando di satelliti piuttosto lontani dal pianeta, consideriamo la traiettoria del satellite rettilinea nell’intorno che ci interessa. L’arco di cerchio è talmente piccolo che l’approssimazione non inficia il risultato, come si può vedere facilmente ad occhio nella Fig. 1 (ma non guardatela ancora...).

Ovviamente, per far riuscire il piccolo "quiz" è necessario partire in condizioni ideali. Ossia, immaginate che vi sia la prima eclissi quasi subito... Adesso, prima di proseguire, pensateci un po' e non andate al computer e non fate "partire" programmi speciali, ma usate carta e matita. Sono più che sufficienti!

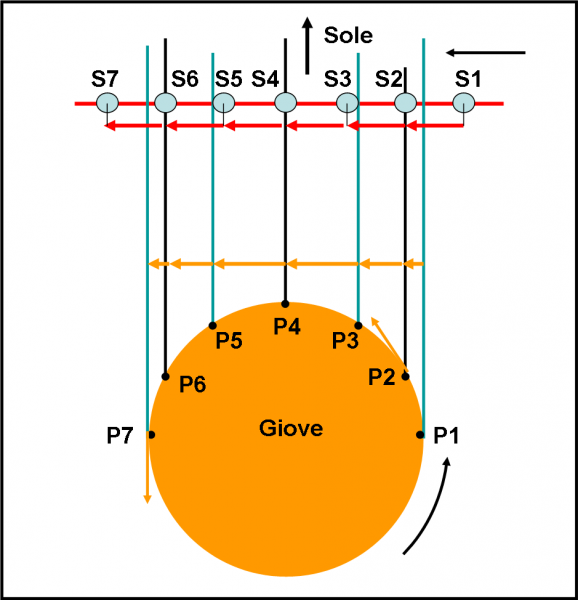
Il punto P sia un punto sulla superficie di Giove. S, sia invece il satellite che viaggia con un velocità leggermente inferiore a quella di rotazione di Giove. Consideriamo sette posizioni scelte “ad hoc” per il punto P, ognuna separata da quella precedente di un angolo al centro di 30°. La velocità tangenziale del punto P è sempre la stessa, ma a noi interessa calcolare la sua componente parallela alla traiettoria del satellite per confrontarla con la velocità costante di quest’ultimo.

Sappiamo fare benissimo la scomposizione di un vettore e quindi possiamo tranquillamente dire che la componente della velocità del punto P di Giove è proporzionale alle frecce arancioni. Essa è ovviamente uguale a zero nel punto iniziale e nel punto finale, mentre è massima a 90° da questi due punti. Il satellite, invece ha velocità costante lungo la sua linea orizzontale ed essa è proporzionale alle freccette rosse. Non ci resta, adesso, che confrontare le due frecce di diverso colore. Ancora più facilmente, disegniamo la posizione del punto P e quella corrispondente del satellite S.

Dai vari punti P1, P2, … P7, separati di 30°, tracciamo le parallele dirette verso il Sole. Solo se qualcosa si trova lungo queste rette si ha un eclissi di Sole. Il tutto si risolve disegnando come si sposta, durante la rotazione di Giove, questa retta (relativa a P), diretta verso il Sole, e controllare dove si trova il satellite in quel momento.

Per ogni punto P, disegniamo , perciò, la corrispondente posizione del satellite da S1 a S7, che si muove in modo costante. Nel tempo che il punto P descrive un arco di 30°, il satellite S si sposta di un segmento sempre uguale.

Quando P è in P1 il satellite è in S1. Esso si trova nettamente a destra della linea azzurra e quindi non causa alcuna eclisse di Sole. P si muove, ma la sua componente è molto piccola e così giunge in P2 quando il satellite arriva in S2. Quest’ultimo si interpone al Sole e P vede un’eclisse totale.

Il satellite prosegue nella sua corsa costante e giunge in S3, mentre P3 si sposta di meno lungo tale direzione. In poche parole, il satellite è adesso davanti rispetto alla direzione del Sole e non vi è eclissi. Finalmente P può scatenarsi e mostrare una componente di velocità che supera quella sempre costante del satellite. E’ P ad andare più veloce e a recuperare il terreno perso in precedenza e raggiunge S quando è in S4 e lui in P4. Abbiamo un'altra eclissi di Sole dello stesso satellite nello stesso giorno gioviano.

Il punto P continua  a correre e viaggia più veloce di S arrivando in P5, mentre S arriva solo in S5. Questa volta il satellite si trova dietro alla retta azzurra: nessuna eclissi di Sole. Il punto P ha dato il suo massimo e ora è costretto a rallentare, ossia la componente della sua velocità diminuisce. Il satellite invece continua senza cedimenti e riesce a riagguantare la retta nera verso il Sole di P6 nella posizione S6. E tre! Abbiamo la terza eclissi di Sole. P è ormai stremato e si sposta di pochissimo per arrivare in P7, mentre il satellite è ormai ben più avanti in S6. Oltre alle eclissi si è notato molto bene il movimento apparente, in avanti e indietro, del satellite rispetto a P.

No, non c’è bisogno di Stellarium o di Celestia o di chissà che altro programma informatico. Basta un po’ di ragionamento, un briciolo di conoscenza dei moti orbitali e una matita bene appuntita… Questo è il nostro sistema di approccio all’Universo: cercare di semplificare, di capire il perché, il come e il quando. Solo dopo ci si può anche divertire con le simulazioni fatte dai soliti programmi concettualmente inutili.

Mi fermo qui… Abbiamo distrutto un "mistero" con un sola figura. In seguito, magari, vedremo che questo discorso è collegato strettamente alla traiettoria apparente dei pianeti nel cielo, che gli antichi greci avevano dovuto risolvere in modo complicatissimo a causa dell’ipotesi geostazionaria.

Sono convinto che coloro che hanno seguito gli articoli sui fenomeni mutui dei satelliti gioviani sono stati in grado di risolvere il problema da soli. Il ragionamento batte il computer sempre e comunque! Usiamo quest'ultimo solo come "stupido" servitore e mai come portatore di verità assolute da prendere a scatola chiusa. A noi basta il concetto, le raffinatezze possono arrivare dopo e non sono veramente importanti.