Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Il prodotto vettoriale ci ha fatto conoscere il momento angolare, una grandezza veramente interessante. Essa deriva direttamente dalla quantità di moto, ma ha il privilegio di rimanere costante anche in “alcuni casi” in cui la quantità di moto può essere costretta a variare. E questi sono casi estremamente interessanti in meccanica… Queste situazioni le vedremo meglio tra poco.

Torniamo al concetto di momento di un vettore. Lo possiamo applicare a qualsiasi vettore e quindi perché non applicarlo a una forza F? In parole povere, tutto il procedimento usato per definire il momento della quantità di moto (ossia il momento angolare) può essere ripetuto per la forza F. Le figure rimangono praticamente le stesse, ma tanto vale riproporle. In  Fig. 23 consideriamo il solito punto O e la forza F applicata in P. chiamiamo come al solito r il vettore che unisce O con P.

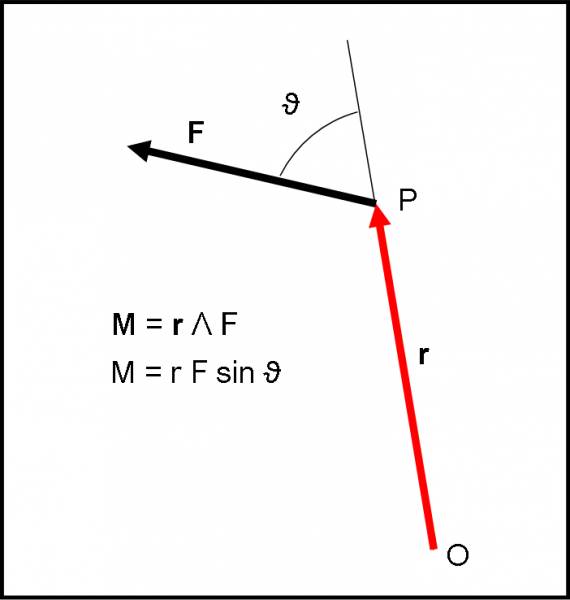
Eseguiamo il prodotto vettoriale tra r e F e otteniamo il vettore  M:

r Λ F = M

il cui modulo è ovviamente:

M = r F sinϑ

Come ormai sappiamo bene, questo vettore è perpendicolare al piano definito dalla forza e dal punto O e il suo verso segue la regola della vite o della mano destra (come preferite). Per analogia con quanto fatto finora chiamiamo questo vettore momento della forza F.

Anche per lui potremmo utilizzare le due componenti (radiale e tangenziale) e notare subito che l’unica componente che determina il risultato finale è quella ortogonale al vettore r. In modo perfettamente analogo a quanto ottenuto per il momento angolare, come mostra la Fig. 24.

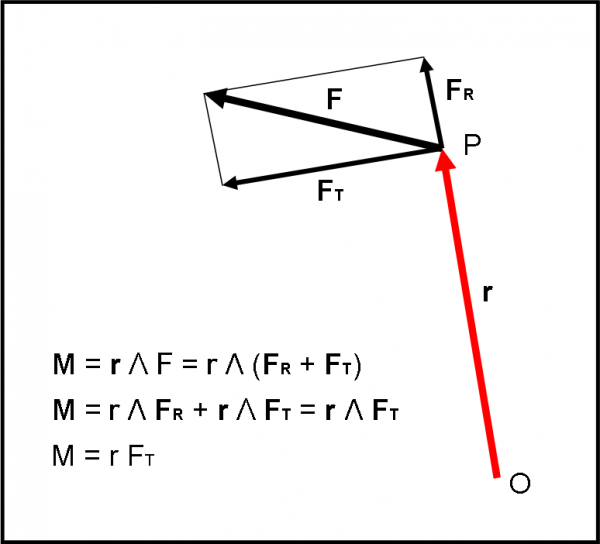
Ricordiamo ancora un punto fondamentale che vale per qualsiasi “momento”. Ha senso parlare di momento (di un vettore qualsiasi, sia esso una quantità di moto o una Forza) solo se indichiamo, sempre, rispetto a quale punto O si riferisce. Senza punto O non esiste r e quindi non esiste alcun momento…

Cosa vuol dire applicare un momento di una forza al punto O. Da un punto di vista “pratico”, il concetto è abbastanza semplice… Immaginate che r sia veramente collegato fisicamente a P. La forza F imprime un’accelerazione a P e lo fa muovere nella direzione del vettore. Varia di conseguenza l’angolo ϑ e si ottiene una rotazione del vettore r. Una rotazione che avviene attorno  a un asse che coincide proprio con il momento della Forza (Fig. 25).

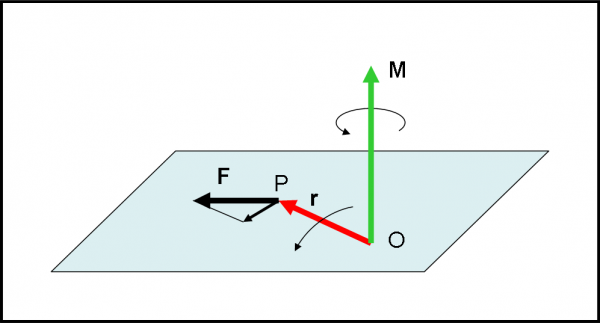
Se poi obblighiamo r a non allungarsi o ad accorciarsi, otteniamo un moto circolare. Qualcosa di simile a quanto avevamo ottenuto per il momento angolare. In quel caso la velocità era a modulo costante e determinava un moto circolare uniforme. Questa volta è costante il modulo della forza, ossia quello dell’accelerazione. Ne risulta un moto circolare ad accelerazione costante e quindi una velocità variabile anche in modulo. In ogni modo, il momento della forza rimane costante.

Prima di scrivere il tutto in modo più sintetico attraverso poche e banali formule, vediamo di fare il punto della situazione legando tra loro il momento di una forza e il corrispondente momento della quantità di moto (momento angolare).

Se applichiamo una forza F a P, di massa m, sappiamo benissimo che facciamo variare la sua quantità di moto, dato che F è proprio la variazione della quantità di moto rispetto al tempo (ricordate?). Se F non è zero, non lo è nemmeno la variazione della quantità di moto. Tutto ciò era stato riassunto dicendo che la quantità di moto si conserva se la risultante delle forze applicate a P è nulla.

Non ci vuole molto a spostare il ragionamento a momento angolare e a momento di una forza. Un momento angolare rimane costante finché è costante la velocità. Se si applica una forza F alla massa m di P, varia il suo momento angolare, dato che varia il vettore velocità. Ne consegue che un punto P mantiene un momento angolare costante solo se è uguale a zero la risultante dei momenti delle forze che gli sono applicate. Attenzione: non ho detto che è nulla la risultante delle forze che gli sono applicate, ma il momento delle forze.

Perché…? Farebbe una qualche differenza? Ebbene sì. E’ vero che se la forza fosse uguale a zero, la quantità di moto si conserverebbe e quindi anche il momento angolare, ma è anche vero che sarebbe una condizione troppo restrittiva! Potrebbe anche essergli applicata una forza tale da far variare la quantità di moto, ma, nel contempo, mantenere costante il momento angolare. E’ possibile? Sicuramente sì! Ne abbiamo già visto un caso perfetto: il moto circolare uniforme.

In questo caso, su punto P agisce una forza, quella centripeta, ma il momento angolare NON cambia. Si capisce subito, quindi, che per far variare oppure no il momento angolare non possiamo limitarci alle forze, ma introdurre i momenti delle forze. Insomma i vettori seguono i vettori, mentre i prodotti vettoriali seguono i prodotti vettoriali (ossia i momenti seguono i momenti).

Concludiamo facilmente. Affinché una forza non sia nulla, ma sia nullo il suo momento, è necessaria una sola cosa: che la forza F sia parallela al vettore r, ossia la componente perpendicolare sia uguale a zero. Beh… la forza centripeta è proprio un classico esempio di tale forza, dato che è diretta sempre e comunque verso il punto O.

Come al solito abbiamo usato tante parole, ma il tutto poteva essere sintetizzato come segue.

Sia L il momento angolare, F la forza e M il suo momento. Possiamo scrivere:

L =  r Λ mv  

dL/dt = d(r Λ mv)/dt = (dr/dt) Λ mv + r Λ d(mv)/dt

Come al solito, però, (dr/dt ) Λ mv = 0 (vettori paralleli), e quindi:

dL/dt =  r Λ d(mv)/dt

Tuttavia, sappiamo molto bene che la derivata rispetto al tempo della quantità di moto non è altro che la forza F, per cui:

dL/dt = r Λ F = M

Una formula fondamentale, anche se ovvia nella sua determinazione. Essa dice che il momento di una forza rispetto a un punto O non è altro che la derivata del momento angolare rispetto allo stesso punto O.

Qualsiasi sia F, l’importante è, quindi, ciò che succede a M. Se M è diverso da zero, il momento angolare è costretto a variare e non può rimanere costante. L’unico modo perché L rimanga costate è porre:

M = 0

Infatti:

dL/dt = 0

e infine

L = costante

Ribadiamo ancora il concetto finale di quanto scritto sia con le parole che con la matematica (ridicola veramente…): il momento angolare di un punto di massa m si conserva se è nullo il momento  delle forze che agiscono su di lui. Potrebbero anche essercene cento, ma se il momento risultante è zero, il momento angolare rimane costante.

Notiamo ancora una volta l’analogia con quanto abbiamo trovato per la quantità di moto: la quantità di moto di un punto di massa m si conserva se è nulla la risultante delle forze che agiscono su di lui. Ovviamente le forze interne si annullano, così come i momenti delle forze interne (i più bravi avranno già capito perché la pattinatrice su ghiaccio deve conservare il momento angolare: la forza che gli fa spostare le braccia è interna al sistema!).

La prossima volta applicheremo questi risultati al moto circolare utilizzando le nuove grandezze appena conosciute. Il momento angolare ci sta per svelare le sue proprietà. Niente di strano e imprevedibile (a questo punto) ma le conseguenze sono fondamentali! Faremo anche la conoscenza di un qualcosa che imita perfettamente la massa inerziale.