Chi non ha mai visto una delle figure più usate in letteratura per rappresentare i buchi neri come deformazioni dello spazio-tempo? Mi riferisco ai celebri “imbuti”. Una geniale descrizione grafica che deve essere, però, capita con tutti i suoi enormi limiti. Cerchiamo di costruirla e di capire quanto sia “fittizia” e quanta confusione potrebbe creare se non interpretata correttamente.

Vorrei mostrarvi come si arriva a una delle rappresentazioni più utilizzate ed efficaci dei buchi neri, ma che, come tutto ciò che si disegna su un foglio e che si riferisce a uno spaziotempo quadrimensionale, è completamente “sbagliato”. O, meglio, va interpretato per quello che è, senza cercare di vedere più in là dei suoi limiti intrinseci. Proprio la parola “intrinseco” è una delle caratteristiche da tenere bene a mente quando si parla di uno spazio. So che la soluzione migliore sarebbe quella di descrivere compiutamente cosa s’intende per spazio curvo, ma porterebbe a un nuovo argomento estremamente lungo e non banalissimo. Come già detto altrove, lo tratterò sicuramente, ma, per quanto riguarda i buchi neri e le loro rappresentazioni, cercherò di utilizzarne solo la parte più intuitiva, commettendo -magari- anche qualche errore veniale. L’importante è afferrare il concetto fondamentale.

Mi riferisco al buco nero raffigurato come un “imbuto”, una delle visioni più classiche, che dovrebbe fornire una visione dello spazio deformato dalla gravità attraverso il famoso tessuto “elastico” su cui vengono poste delle sfere massicce che creano avvallamenti più o meno profondi. Per risparmiarmi molte e inutili parole, inserisco un classico disegno di questo tipo nella Fig. 1.

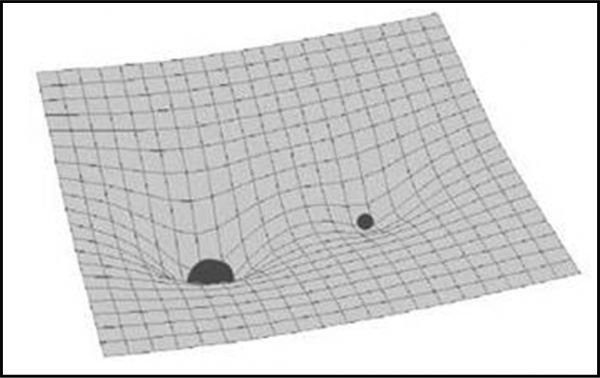
Si ha un buco nero quando l’avvallamento sprofonda all’infinito, in un vero e proprio tubo senza fine. Una splendida e brillante rappresentazione che va però intesa per quello che è, senza cercare di vedere anche quello che non si può vedere. Si rischierebbe di fare molta confusione e di partire con il piede sbagliato.

Cerchiamo di costruirlo insieme, facendo molta attenzione al suo reale significato. Prima di iniziare,  poche frasi per spiegare cosa s’intende per curva e curvatura.

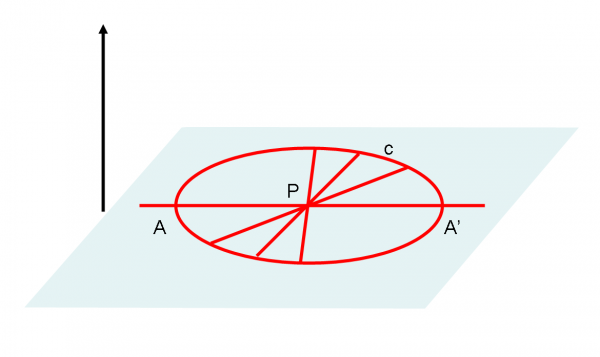
Il piano del foglio rappresenta molto bene un piano euclideo, in cui si possono disegnare sia rette che linee curve. Il concetto di curvatura esiste sicuramente in uno spazio piano: un cerchio ha una curvatura reale che si può misurare benissimo rimanendo nel piano euclideo. Questo tipo di curvatura è intrinseca allo spazio considerato, dato che pur vivendo nelle sue dimensioni è sempre verificabile in qualche modo. Pensiamo a Flatlandia e a un punto che vive su uno spazio a due dimensioni. Esso può sicuramente dire che sta andando in linea retta oppure sta girando in tondo, attraverso punti di riferimento e/o varie accortezze. Vediamo questo mondo in Fig. 2.

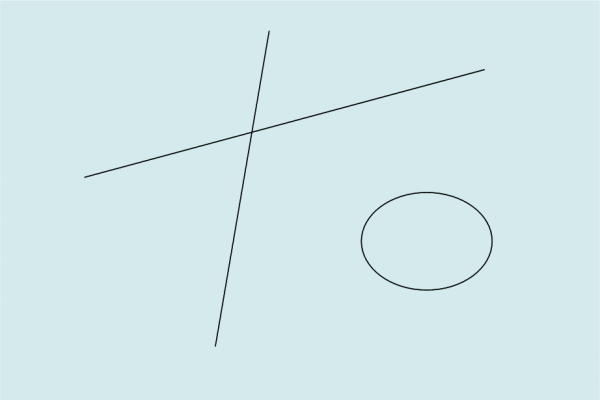
Noi, esseri a tre dimensioni, possiamo facilmente disegnare l’intero piano euclideo a due dimensioni nel nostro spazio a tre come riportato in Fig. 3. Aggiungiamo una terza dimensione e il gioco è fatto.

Eseguita questa immersione di uno spazio a due dimensioni in uno spazio a tre, possiamo concludere che ciò che appariva rettilineo, vivendo nello spazio a due dimensioni, resta rettilineo nello spazio a tre e ciò che era curvo nelle due dimensioni rimane curvo anche nelle tre. Le curvature intrinseche sono anche estrinseche, ossia si notano anche nello spazio a tre. D’altra parte, sia in due che in tre dimensioni, siamo pur sempre in uno spazio euclideo dove valgono le stesse regole geometriche.

Diciamo, in altre parole, ciò che abbiamo fatto e quello che osserviamo. Le rette iniziali sono intrinsecamente rette e le curve sono intrinsecamente curve. Esse seguono certe regole matematiche che le classificano come tali vivendo all’interno delle due dimensioni. Aggiungendo una dimensione, come facciamo a vedere se le nostre linee conservano le caratteristiche precedenti? Facilissimo: le confrontiamo con rette e curve dello spazio a tre dimensioni. Se essere restano tali anche in questo nuovo sistema le curve diventano estrinseche.

Adesso dobbiamo fare un piccolo sforzo di immaginazione e considerare uno spazio a due dimensioni curvo. In parole povere, su di esso valgono regole matematiche e geometriche non euclidee. Vivendo in tale spazio a due dimensioni curvo, possono, comunque, esistere sia rette che linee curve intrinseche. In altre parole, chi vive su di esso lo può rappresentare come quello della Fig. 2. Due abitanti di questi spazi bidimensionali potrebbero raccontarsi molte esperienze identiche. Cambierebbero soltanto le regole matematiche con cui descrivono il loro mondo. Stiamo, ovviamente, considerando abitanti abbastanza intelligenti e bravi disegnatori. Pur vivendo in due dimensioni sono capaci di disegnare in due dimensioni, così come noi che viviamo in tre dimensioni siamo capaci di disegnare in tre dimensioni.

Tuttavia, se immergiamo lo spazio curvo a due dimensioni in uno spazio a tre dimensioni molte differenze saltano subito all’occhio. La superficie curva porta alla Fig. 4. Quelle che erano rette diventano curve. Esse sono curve solamente estrinseche che rimangono rette per l’abitante di quello strano mondo.

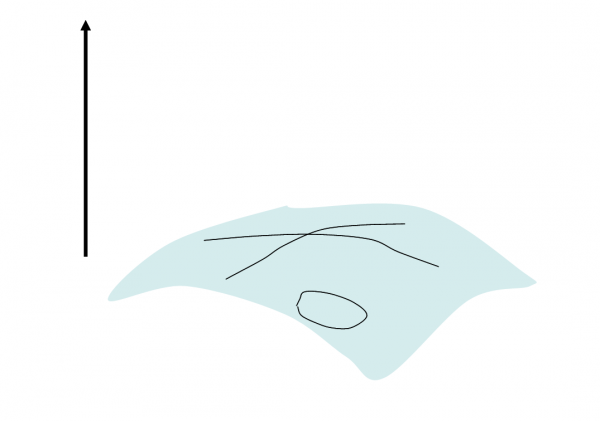
In poche parole, per notare le differenze tra le due superfici (piana e curva) abbiamo avuto bisogno di immergerle in uno spazio a tre dimensioni. Qualcosa che è però del tutto estraneo al “mondo” dei due abitanti. A noi, che viviamo nelle tre dimensioni, è bastato aggiungere una dimensione e osservare il risultato. Ma gli abitanti dei due mondi bidimensionali non potrebbero mai farlo. Loro potrebbero valutare le differenze solo con la matematica. Imprimiamoci molto bene questo concetto nella mente!

Facciamo un ragionamento leggermente più complicato. Noi, abitanti delle tre dimensioni, siamo riusciti a rendere palese la differenza tra due spazi bidimensionali, ma sapremmo fare lo stesso con uno spazio a tre dimensioni? Purtroppo no! Potremmo chiacchierare con un abitante di un altro mondo tridimensionale e confrontare le nostre matematiche che permettono di evidenziare le differenze intrinseche, ma NON potremmo certo aggiungere una dimensione per rendere estrinseche le differenze, ossia renderle visibili con semplici figure. I nostri due mondi, descritti entrambi nelle tre dimensioni, avrebbero -magari- la stessa identica forma, così come succedeva per gli abitanti bidimensionali. Non è facile mostrare questa situazione, ma ci deve bastare il sapere che gli stessi problemi delle due dimensioni si devono avere nelle tre, nelle quattro, nelle cinque, ecc., ecc. La matematica lo riesce a dimostrare molto bene e ne abbiamo già parlato in questo articolo.

Ci troviamo, così, di fronte a un grande bivio. Abbiamo due possibilità per descrivere uno spazio a tre dimensioni vivendoci all’interno. O accettarlo per quello che è e descriverlo attraverso la matematica (ed è quello che fanno le formule della relatività generale, ad esempio), oppure utilizzare uno spazio a due dimensioni e rappresentarlo in modo estrinseco aggiungendo una dimensione in più del tutto arbitraria che non fa parte del mondo a due dimensioni. Non ci è, infatti, possibile aggiungere al nostro mondo di tre dimensioni una quarta dimensione per vederlo in modo estrinseco. Non ne siamo assolutamente in grado.

Siamo, perciò, costretti a  fare una dura scelta. I matematici scelgono sicuramente la prima soluzione, anche se non gli permette di fare figure veramente esplicative. Noi, invece, che vogliamo capire i concetti più che perderci nelle formule, scegliamo il secondo. Ovviamente, non lo facciamo solo noi, ma quasi tutti i libri di divulgazione. Quante volte abbiamo visto un buco nero rappresentato con la figura a “imbuto”? Bene, essa non descrive la matematica intrinseca dello spazio curvo a tre dimensioni, ma solo e soltanto uno spazio curvo a due dimensioni utilizzando una dimensione aggiuntiva del tutto arbitraria.

Mi raccomando, quindi, di tenere sempre a mente questo concetto fondamentale e non facciamoci ingannare dalla accattivante figura che ci mostra il buco nero come un vero e proprio inghiottitoio. Non confondiamo mai l’ apparenza di una rappresentazione parziale con la realtà dei fatti. L’imbuto resta sempre una rappresentazione di uno spazio a due dimensioni osservato in modo estrinseco, avendo aggiunto una dimensione che non fa certo parte di lui: non confondiamola, quindi, con la terza dimensione di uno spazio curvo a tre dimensioni. Spero di essere stato sufficientemente chiaro. Se avete problemi a riguardo fatemelo sapere subito! Non possiamo portarci dietro una visione “falsa”, prendendola per “vera”.

Per comprendere meglio ciò che si fa costruendo il bellissimo imbuto, scegliamo una superficie curva molto semplice, che conosciamo bene, dato che, in fondo, stiamo proprio vivendo su di lei anche se siamo a tre dimensioni. Questa superficie è la sfera. La conosciamo bene perché la Terra è una sfera piuttosto accurata. Camminando su di lei ci rendiamo immediatamente conto della geometria del tutto assurda rispetto a quella piana o tridimensionale di tipo euclideo. La tratteremo accuratamente in futuro, dato che è estremamente importante non solo come esempio di superficie curva nel contesto della relatività generale  e dei buchi neri, ma proprio perché le coordinate celesti e le regole di trigonometria sferica hanno bisogno della sua matematica.

Torniamo a noi e dedichiamoci anima e corpo all’imbuto che è e rimarrà sempre una rappresentazione bidimensionale vista in modo estrinseco attraverso l’aggiunta di una dimensione arbitraria.

Richiamiamo solo alcune ben note caratteristiche della superficie sferica e di come vengono viste in modo intrinseco da chi ci vive. Ad esempio, viaggiando su un cerchio massimo si è convinti di andare lungo una linea retta e invece prima o poi ci si ritrova al punto di partenza. Succederebbe lo stesso se si andasse lungo un parallelo. Tuttavia vi è una netta differenza tra i due percorsi. La descrizione matematica della prima traiettoria ci assicurerebbe che siamo proprio su una linea retta intrinseca, mentre nel secondo caso capiremmo di effettuare un percorso curvo altrettanto intrinseco.

Come già detto, anche su una superficie curva possono esistere sia rette che curve intrinseche. Non esisteranno più rette solo quando si passa a una visione estrinseca, dopo aver aggiunto la ormai famosa dimensione arbitraria.

Consideriamo il disegno di Fig. 5.

Stiamo osservando una superficie piana, ma potremmo anche osservare una superficie sferica. Il risultato sarebbe, infatti, identico sotto molti aspetti. La figura è infatti doppia, dato che ci è stata fornita sia da chi vive nel piano euclideo, sia da chi vive su una superficie sferica. C’è poco da fare: entrambi vivono in una superficie a due dimensione e non possono certo inserire una terza dimensione che per loro non esiste.

Figure uguali in apparenza, perché se confrontassimo la matematica che le descrive sarebbe decisamente diversa. Nella prima, ad esempio, la somma degli angoli di un  triangolo è uguale a 180°, nell’altra no. Nella prima, rette "parallele" non si incontrano mai, nella seconda sì. Come detto, però, noi non vogliamo immergerci nella matematica. Preferiamo immergere le due figure bidimensionali in uno spazio a tre dimensioni, attraverso l’aggiunta di una terza dimensione arbitraria.

Se facciamo questa operazione otteniamo figure completamente diverse.  La Fig. 6 trasporta una superficie piana in uno spazio tridimensionale. Non cambia assolutamente nulla, dato che la terza dimensione non è veramente arbitraria, ma è quella che permette di passare da un piano euclideo a uno spazio tridimensionale euclideo. Le curve intrinseche rimangono curve, e le rette rimangono rette.

Ben diversa è la situazione se aggiungiamo una dimensione arbitraria a una superficie curva. Otteniamo la Fig. 7.

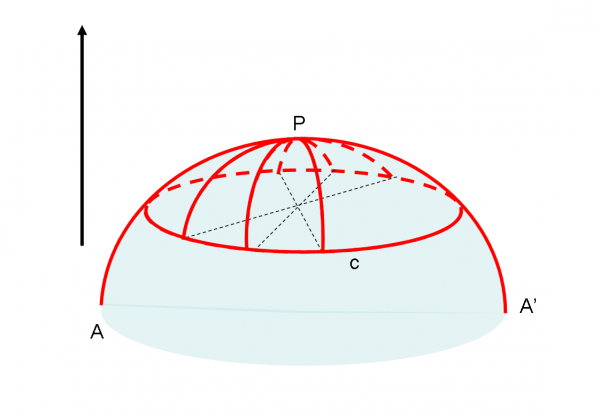
La curva intrinseca è rimasta una curva, ma le rette sono ora diventate delle curve. Sono perciò curve solamente estrinseche. Curve reali per la nostra visione tridimensionale, ma sempre rette per chi vive sulla superficie sferica (scusate se mi ripeto, ma il concetto è veramente fondamentale). Attenzione che le linee tratteggiate sottili NON appartengono alla superficie, ma a uno spazio del tutto estraneo alla superficie curva.

Qualcuno potrebbe dire: “Va bene, va bene, abbiamo capito la differenza e sappiamo anche come evidenziarla. E’ bastata un’occhiata alla visione estrinseca e adesso possiamo tornare alle due dimensioni, sapendo come agire. Anzi, siamo talmente bravi che se ci riuscissimo, potremmo anche tentare di descrivere uno spazio a tre dimensioni senza matematica e senza utilizzare la quarta.” No, mi spiace, sarebbe un illuso.

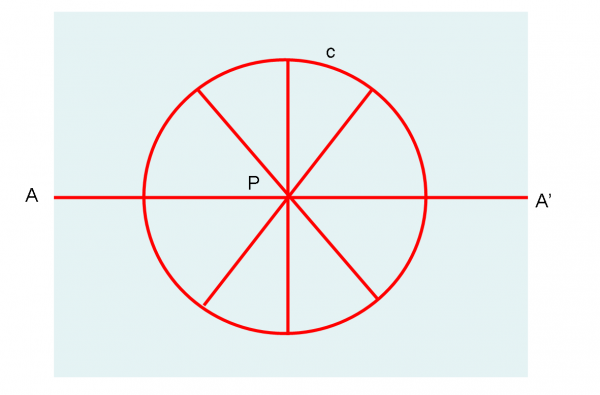
Torniamo alla Fig. 5 (quella comune alle due superfici)  e vediamo subito cosa succede. Disegniamo la Fig. 8 e parliamo finalmente di astronomia.

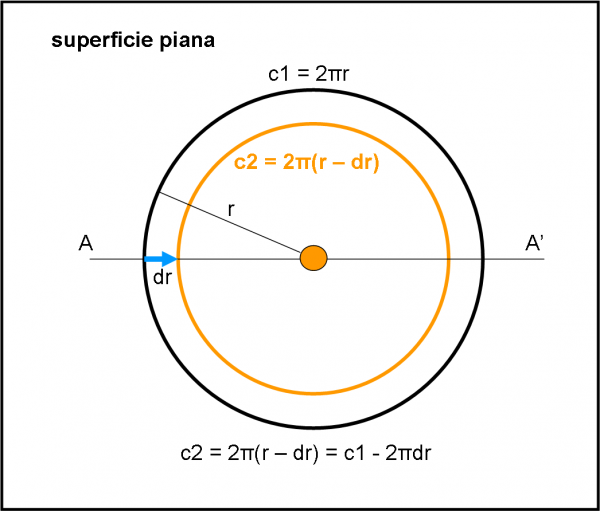
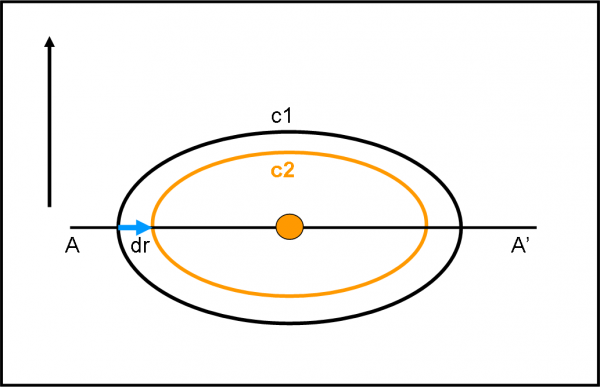
Al centro mettiamo il Sole e la circonferenza c1 sia l’orbita di un pianeta attorno a lui. La sua lunghezza è data da c1 = 2πr. Consideriamo il caso piano, ossia consideriamo di trovarci sul piano di c1. Il Sole si fa sentire attraverso la legge di Newton, ossia la gravità. Uno corpo che descrive la traiettoria c1 lo fa seguendo la meccanica classica. Nessun problema a lavorare su questo piano. In particolare, eseguiamo una piccola operazione. Spostiamo l’orbita c1 più vicina al Sole. Ci basta accorciare il raggio dell’orbita della quantità dr. Quanto vale la lunghezza dell’orbita c2? Un gioco da bambini:

c2 = 2π(r –dr) = 2πr - 2πdr = c1 - 2πdr

Cosa possiamo dire? La seconda circonferenza è uguale alla prima meno una quantità data da 2πdr.

Fin qui tutto bene.

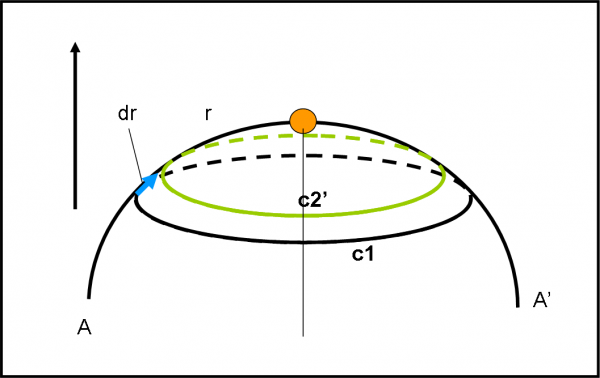
Ecco, però, che un certo Signor Einstein decide (e dimostra) che lo spazio a due dimensioni che abbiamo considerato piano (ed euclideo) è invece uno spazio a due dimensioni curvo (non euclideo). Poco male. Vuol dire che la Fig. 5 si riferisce a una superficie curva. Disegniamola nuovamente nella Fig. 9, anche se non ce ne sarebbe bisogno, dato che l’apparenza delle due superfici può sembrare la stessa, per chi ci vive dentro, come già dimostrato.

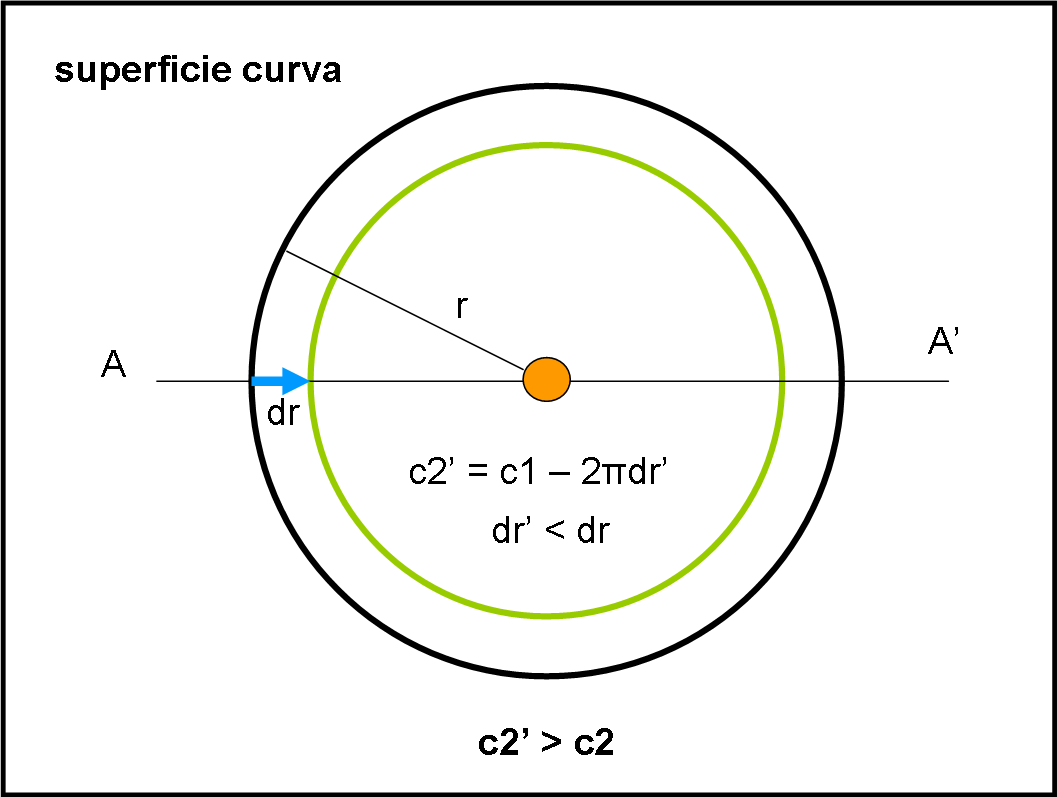
Facciamo la stessa operazione di prima e accorciamo la distanza r tra pianeta e Sole di dr. Misuriamo nuovamente la lunghezza della nuova circonferenza verde c2’. Il nuovo raggio sembrerebbe essere r – dr, come prima, da cui seguirebbe che anche c2’ deve essere uguale a c2. Le formule per calcolare la lunghezza di una circonferenza le conosciamo bene.

Effettuiamo la misura come abitante della superficie sferica e troviamo che il risultato è decisamente diverso:

c2’ > c2

E’ come se alla circonferenza c1 di partenza avessimo tolto una quantità più piccola rispetto a quanto fatto per c2. Accidenti, questo non ce lo aspettavamo! Oppure sì? In fondo, sapevamo benissimo che la matematica delle due superfici è diversa. Purtroppo, non possiamo disegnare sulla stessa figura due  circonferenze che hanno lo stesso raggio e che hanno, però, lunghezze diverse o viceversa. La nostra rappresentazione a due dimensioni ci ha già … fregato! Facendo i calcoli attraverso la matematica dei due mondi, troveremmo il motivo di questa differenza a prima vista “assurda”. In realtà, accorciando il raggio di dr nella superficie piana, noi lo abbiamo accorciato di dr’ < dr nella superficie curva vista in maniera estrinseca. Tuttavia, nella rappresentazione a due dimensioni entrambi gli abitanti assicurano di averlo accorciato della stessa quantità dr.

Non ci resta che  tornare nuovamente, anche se a malincuore, alla visione estrinseca, ossia a quella che si ottiene aggiungendo la terza dimensione arbitraria.

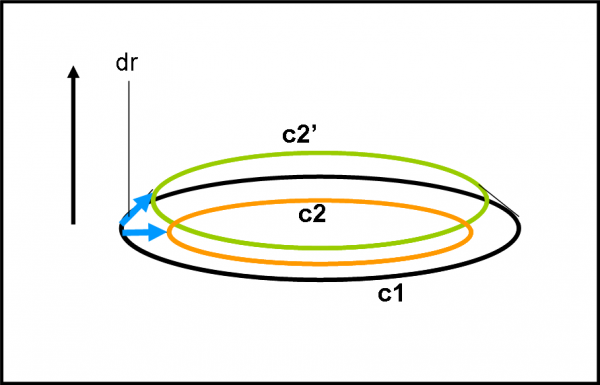
Nel caso della superficie piana (meccanica classica) otteniamo la Fig. 10. Tutto rimane come prima e non potevamo che aspettarcelo, dato che la superficie era un piano euclideo.

Nel caso della superficie curva (sferica nell’esempio che facciamo) otteniamo, invece la Fig. 11. Mamma mia, le cose sono profondamente cambiate (e dovevamo aspettarcelo).

Possiamo tentare di capire, in modo molto qualitativo, questa anomalia, chiedendoci: “Come mai la circonferenza c2’ è più lunga di c2?”. Usiamo la Fig. 12 che ne dà una spiegazione abbastanza comprensibile. Le cose sono molto più complicate, ma la figura permette una visione abbastanza “esplicativa”. E’ come se avessimo accorciato un arco di cerchio e non un raggio e quindi la circonferenza tracciata sulla superficie curva è maggiore di quella del caso piano.

Non andiamo per il sottile (dovremmo introdurre la geometria sulla sfera) e pensiamo, per adesso, a rappresentare quanto trovato. Sicuramente la seconda circonferenza tracciata nella superficie curva è più lunga di quella tracciata sul piano. Per adesso fidiamoci e accontentiamoci.

Cosa dobbiamo fare in pratica? Lo vediamo nella Fig. 13.

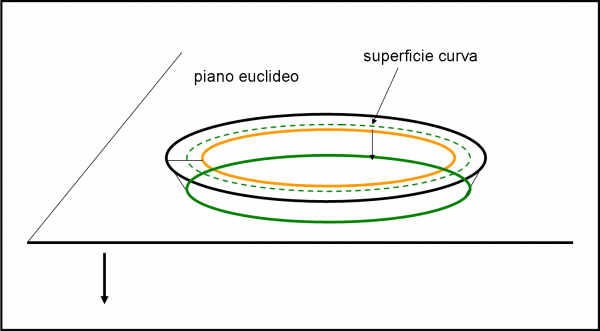
Disegniamo un bel piano euclideo, dove le deformazioni di curvatura del Sig. Einstein sono trascurabili. Tracciamo la nostra bella circonferenza c1 che appartiene a entrambe le superfici (quella piana e quella curva). Sul piano euclideo tracciamo la circonferenza che si ottiene riducendo il raggio, ma senza curvare la superficie. Nella superficie che inizia a curvarsi, però, questa circonferenza arancione non va più bene, dato che è troppo corta. Deve diventare quella verde. Ma non possiamo certo farlo sul piano euclideo. Saremmo costretti ad accartocciare in qualche modo il foglio per far coincidere circonferenza arancione e circonferenza verde. Ma “accartocciare” non è un verbo che ha senso in un piano, dato che implica una dimensione ulteriore “effettiva” che non esiste.

Dobbiamo, perciò, introdurre una dimensione aggiuntiva, del tutto fittizia, che ci permetta di disegnare la nuova circonferenza verde. La possiamo disegnare solo un  po’ più in basso dell’altra e il nostro imbuto comincia a formarsi (potevamo anche disegnarla in alto, ma non avrebbe reso l’idea della “caduta” senza fine). Andando avanti in questo modo, e tenendo conto che la curvatura aumenta sempre di più andando più vicini al Sole, si ottiene la classica Fig. 14.

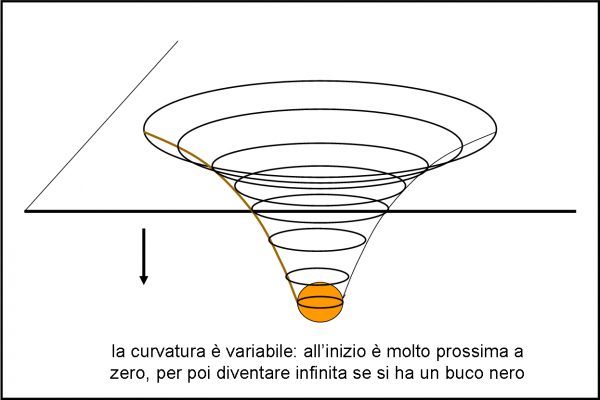
Potevamo disegnare tutto su un piano? Sicuramente sì, ma le varie circonferenze sarebbero state concentriche, complanari e le variazioni effettive della distanza dal Sole non corrispondenti al vero raggio delle circonferenze, dato che le distanze si misurano sulla superficie. Insomma qualcosa che non sarebbe stato né carne né pesce e che solo la matematica sarebbe in grado di descrivere.

In parole molto povere, possiamo dire che costruiamo una superficie curva bidimensionale, di curvatura variabile, in maniera estrinseca.

Nel caso che il Sole sia un buco nero, la curva marrone piega sempre di più fino a diventare una retta verticale. Retta verticale vuole dire curvatura zero, ma, rispetto al piano euclideo di partenza, vuol dire curvatura infinita. Non è un concetto banale, ma non perdiamoci troppo tempo, dato che quella linea, comunque, non rappresenta certo la vera curvatura dello spazio a tre dimensioni, ma è legata solo e soltanto a uno spazio bidimensionale (e nemmeno esattamente).

Oltretutto, non dimentichiamo mai che nel caso reale non solo non abbiamo uno spazio a due dimensioni, ma addirittura uno spaziotempo a quattro dimensioni! Tuttavia, la forma a imbuto è molto affascinante e rende bene l’idea di qualcosa che inghiotte tutto ciò che capita a tiro e di una caduta  incontrollabile.

Dobbiamo però notare ancora una volta due fatti fondamentali che devono metterci sempre sul chi vive. Innanzitutto, non possiamo dimenticare che la dimensione aggiunta non ha alcun significato fisico. Non esiste realmente una terza dimensione in cui la superficie s’incurva, ma è la stessa superficie ad essere curva. Inoltre, vediamo che si inserisce spesso la stella o il buco nero al fondo dell’imbuto. L’idea che si cerca di dare è che il tessuto spaziotemporale sia una membrana elastica che viene deformata da una sfera massiccia che viene inserita su di lei. Questo concetto è un po’ fuorviante, dato che non esiste gravità al di fuori della membrana, ma solo su di lei. Niente può essere depositato sopra di lei. La membrana non si deforma lungo una qualsiasi dimensione esterna, ma è essa stessa che si curva producendo gli effetti gravitazionali.

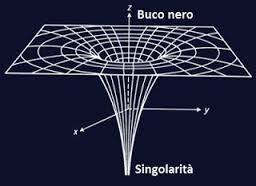
La Fig. 15 è una classica visione a imbuto di un buco nero. L’aggiunta degli assi x, y  e z è, però, gravemente fuorviante, dato che potrebbe far pensare alle nostre tre dimensioni. Assolutamente niente di tutto ciò, come abbiamo cercato di far capire, anche se in modo molto qualitativo…

Quest’articolo può risultare un po’ ostico e poco intuitivo. Tuttavia, mi sentivo in dovere di inserirlo prima di parlare e di disegnare i buchi neri di vario tipo. La visione "a imbuto", e molte altre abbastanza simili e fittizie, saranno sicuramente usate.  L’articolo va preso, comunque, per quello che è: cerca di dare un’idea molto rozza della problematica delle superfici e degli spazi curvi. Quando e se riusciremo a descrivere la geometria delle varie superfici curve a partire dai postulati di Euclide, sarà tutta un’altra cosa (magari con qualche asterisco in più…).

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale