Categorie: Fisica classica Terra
Tags: caduta libera foro nella Terra gravità moto armonico
Scritto da: Vincenzo Zappalà
Commenti:41
Quiz: buchiamo la Terra! ****
Personaggi molto influenti dei passati governi italiani non hanno avuto problemi a ideare (e dicono anche a realizzare?) “buchi” attraverso la Terra in modo da farci transitare i poveri neutrini che si sarebbero altrimenti trovati a dover superare tonnellate e tonnellate di dura roccia. Utilizziamo uno di questi tunnel, che congiunge in linea retta due punti della superficie terrestre. Poco importa se questi punti sono o non sono diametralmente opposti. Anzi potete provare a farne uno che passi per il centro della Terra e uno che vada solo da Ginevra al Gran Sasso. Il risultato è lo stesso.
Consideriamo la Terra perfettamente sferica, di densità costante, senza rotazione e, ovviamente, omogenea e fredda. Non sono nemmeno ammesse frizioni e/o attriti. A questo punto non ci resta che far “cadere” un oggetto all’interno del tunnel perfettamente liscio (state tranquilli che cade…). Le domande sono: “Quanto tempo impiega a raggiungere l’altra uscita del tunnel? Ma è sicuro che la raggiunga? E cosa fa se non viene fermato?”
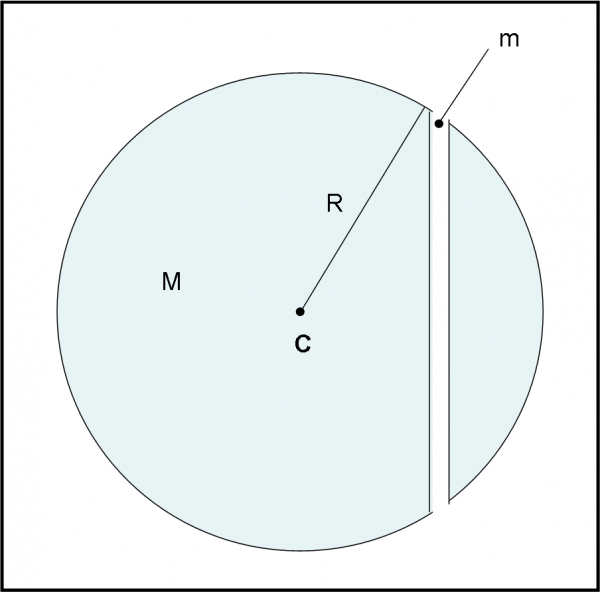
La figura da cui partire è quella che segue.
La massa dell’oggetto è m
La massa della Terra è M = 5.98 · 1024 kg
La costante G vale 6.67 · 10−11 m3/kg · s2
Il raggio della Terra è R = 6.38 · 106 m
Notate che ho fatto il tunnel in senso verticale per facilitare l’idea di una “caduta”, ma potevo disegnarlo anche orizzontale: non sarebbe cambiato niente.
Vi invito, a un certo punto, a dare un’occhiata al moto armonico semplice… quello di un pendolo.
Per Alvy (soprattutto): risponderò solo dopo Capodanno!
Nota Bene: Il problemino è un “classico”, spesso legato alla vecchia barzelletta del verdone mangiasassi, e non è difficile trovare la soluzione sul web (non datemi quella che tiene conto del verdone, però...). Vi invito a non farlo e se già conoscete il risultato non ditelo… grazie!






41 commenti
Bene, avrò quindi un pò di tempo per digerire il cenone d Natale prima di affrontare lo stimolante quiz.
Mamma mia Enzo non vorrei mi rimanesse di traverso il pranzo di Natale...ma no scherzo ovviamente. Aiuto Alvy, chiedi qualcosina...così c'è più tempo per studiarsi il tutto è attendere la risposta...Enziana. Promesso Enzo st0' leggendo e rileggendo e prima o poi, dopo le cene e i pranzi , provo a dire qualcosa anche io.
, provo a dire qualcosa anche io.
puoi sempre usare il verdone mangiasassi che, come l'oggetto cade di un paio di metri, se lo mangia subito!!!!

Comunque, il gioco è sempre lo stesso... forza di gravitazione universale e seconda legge di Newton... come per la massa inerziale e gravitazionale... più o meno! Potresti sempre chiedere alla Signora del tunnel tra il CERN e il Gran Sasso
ah il quiz natalizio enzo visto che a natale sono tutti più buoni dacci almeno qualche aiuttino: se il tunnel fosse scavato passando per il centro(dove hai disegnato il raggio) le risposte cambierebbero drasticamente o no?
enzo visto che a natale sono tutti più buoni dacci almeno qualche aiuttino: se il tunnel fosse scavato passando per il centro(dove hai disegnato il raggio) le risposte cambierebbero drasticamente o no?
Mah, caro Mario, a parte il fatto che io mi chiamo Alvy e non Enzo (di Enzo ce n'è uno solo!), una considerazione che credo possa essere fatta è la seguente.
Bisogna porre attenzione al fatto che mentre la massa m cade verso il centro della Terra, cambia la massa M attraente e quindi si deve modificare di conseguenza l'espressione della forza di attrazione; quest'ultima si modifica continuamente per due ragioni:
- cambia la distanza dal centro di attrazione;
- cambia la massa attraente.
Per trovare la nuova formula didetta forza concentrati sul fatto che la densità è costante; questo semplifica molto le cose. Enzo, molto astutamente, ha posto questa condizione all'inizio dell'articolo anzichè tra le ipotesi in bella evidenza sotto la figura.
Prova a prendere un elastico e tendilo: più lo tendi e più ..... beh, si verifica una cosa del genere!
Mi fermo qui altrimenti Enzo mi uccide.
caro Davide...
va bene che è Natale, ma rileggi bene l'articoletto, dove dice: "Anzi potete provare a farne uno che passi per il centro della Terra e uno che vada solo da Ginevra al Gran Sasso. Il risultato è lo stesso". Anzi, potresti fare il tunnel tra il salotto e la camera da letto (se hai una casa abbastanza grande da notare la curvatura terrestre)...
attento Alvy che l'elastico ti può finire in faccia!!! Per punizione da te voglio anche la dimostrazione del "necessario" teorema di Newton poco conosciuto... (almeno la seconda parte...).
Vabbè Enzo, ma tu sei diabolico!
Non ho detto nulla di decisivo, probabilmente ho solo confuso ulteriormente le idee ....
Toglimi una curiosità Enzo: esiste un articolo in cui venga spiegato qual'è la parte di massa attraente nel caso di un oggetto che precipiti all'interno di .... diciamo un pianeta gassoso (tanto per dare l'idea della penetrabilità)?
Almeno questo concetto avresti dovuto richiamarlo, prima di far diventare matti i volenterosi partecipanti al quiz.
Dai Enzone non volermene ... E poi il buon Mario mi ha chiamato in causa; qualcosa dovevo pur dire, se non altro per educazione...
caro Alvy...
è proprio quello che pretendo da te (si può fare, si può fare da soli...)
scusate.. ma l'oggetto m non dovrebbe "cadere" finche la distanza tra il tunnel eC èridotta al minimo, e poi "adagiarsi" sulla parete del tunnel rivolta verso C?
Operbacco ma che è ste roba
Ciao Enzo, da quel che ricordo di aver letto in gioventù, un libro di curiosità o forse di fantascienza, il tempo di percorrenza di qualunque corda che colleghi due punti della superficie terrestre è uguale. Compreso quello in cui la corda è uguale al diametro. Sarebbe il sistema più veloce per collegare qualsiasi punto della superficie terrestre. Non ricordo più la formula ma si ritrova facilmente in rete... Il risultato è a dir poco impressionante!

Il costo energetico sarebbe nullo!
Ma (sempre a livello teorico), il moto sarebbe veramente perpetuo?
Mi sovviene il titolo di un famoso libro di Eco ...
no comment... per il momento...
Mumble, mumble ,mumble ,ciò che dice beppe mi sembra vero e qui di corda si tratta...si, però qui c'è appunto la gravità che varia avvicinandosi al centro...ma poi ci riallontaniamo...oddio vaneggio e poi mi accorgo ora che c'è un altro articolo.
tranquillo Mario... l'altro è una conseguenza...

Stiamo un po' allargandoci... ma è Natale, via!!!!!
I quiz mi son sempre piaciuti, poiché costringono a ragionare ed anche se si sbaglia a rispondere s'impara sempre qualcosa.
Il quiz da risolvere, io l'ho analizzato sotto il profilo della conservazione dell'energia, d'altronde in questo caso il corpo di massa m viene lasciato cadere, per cui l'energia in gioco è quella generata all'attrazione gravitazionale.
Prima della caduta il corpo di massa m, possiede un Energia Potenziale pari a:
Epot 0 = GMm/r
Assegnando alla massa del corpo il valore di 1 Kg (ma potrei usare qualunque valore, tanto la massa del corpo alla fine risulterà ininfluente)
Epot 0 = GMm/r =2 (6.67 ·10^−11 mt^3/kg s^2 5.98 · 10^24 kg 1 Kg) / 6.38 10^6 mt =
2 (6.67 ·10^−11 mt^2/s^2 5.98 · 10^24 1 Kg) / 6.38 · 10^6 =
2 (39,886· 10^13 Kg mt^2/s^2 )/ 6.38 10^6 =
Epot 0 = 79,7732 10^13 Kg mt^2/s^2 / 6.38 10^6
Epot 0 = 79,7732 10^7 Kg mt^2/s^2 / 6.38 = 125,036 10^6 Kg mt^2/s^2
La sua Energia Cinetica, invece è nulla, infatti:
E c0 = 1/2 m v^2 dato che il corpo m è fermo v = 0 , per cui Ec0 = 0
L'energia totale in gioco deve sempre conservarsi, dato che non vi sono altre forze in gioco oltre alla gravità (razzi che alterano la velocità di m, attriti, ecc.), per cui questa all'inizio vale:
E Totale = E pot 0 + Ec0 = GMm/r + 0 = 125,036 10^6 Kg m^2/s^2
Dopo la caduta il corpo m in un certo tempo raggiunge la sua distanza minima dal centro di massa (centro della terra), ossia il raggio r che separa m dal centro della terra è molto più corto di quello iniziale.
Quanto vale la sua Energia Cinetica? E quella di Potenziale?
Ovviamente, il corpo m si è mosso “spinto” dalla Forza di attrazione gravitazionale, per cui possiede una velocità ed un' Energia cinetica:
Ec1 = 1/2 m v^2
Nel punto più vicino al centro della Terra, la sua Energia di Potenziale vale:
Epot1 = GMm/r1
Supponendo che il punto più vicino al centro della Terra, misuri un raggio pari a 1 10^6 mt
Epot1 = GMm/r1 = 2 (6.67 ·10^−11 mt^3/kg s^2 5.98 10^24 kg 1 Kg) / 1· 10^6 mt
Epot 1 = 79,7732 10^7 Kg m^2/s^2 / 1 = 797,732 10^6 Kg m^2/s^2
Ovviamente, essendo m molto più vicino al centro di gravità, la sua Energia di potenziale risulta più alta di quella di partenza.
L'Energia Totale, però, si deve conservare tenendo conto dell'Energia Cinetica acquisita dal corpo m durante la caduta :
E tot = Epot1 – Ec1
Dato che l'Energia Totale iniziale che si deve conservare è uguale a e Epot0, ne segue, che:
Epot1 = Etot + Ec1
Epot1 = Epot0 + Ec1
Quindi:
GMm/r1 = GMm/r + 1/2 m v1 ^2
GMm/r1 - GMm/r = 1/2 m v1 ^2
Ossia, l'Energia cinetica del corpo m nel suo punto più vicino al centro della terra è pari alla differenza tra l'energia di potenziale Epot1 e quella posseduta all'inizio.
La massa del corpo m come si vede è ininfluente:
GMm/mr1 - GMm/mr = 1/2 v1 ^2
GM/r1 - GM/r = 1/2 v1 ^2
Ora il corpo m possiede una certa velocità (che come si nota non dipende dalla massa del corpo m)
2 (GM/r1 - GM/r) = v1 ^2
2GM/r 1 - 2GM/r = v1 ^2
v1^2 = 2GM/r1 - 2GM/r
Nel caso in questione:
2GM = 2 (6.67 ·10^−11 mt^3/kg s^2 5.98 10^24 Kg) = 79,7732 10^13 mt^3/s^2
v1^2 =79,7732 10^13 mt^3/s^2/r1 - 79,7732 10^13 mt^3/s^2/r
Inserendo il valore di r e di r1
v1^2 = (79,7732 10^13 mt^3/s^2)/ 1·10^6 mt - (79,7732 10^13 mt^3/s^2)/ 6.38 ·10^6 mt
v1^2 = 797,732 10^6 mt^2/s^2 - 125,036 10^6 mt^2/s^2
v1^2 = 672,696 10^6 mt^2/s^2
v1 = (672,696 10^6 mt^2/s^2)^1/2
v1 = 25,936 10^3 mt/s = 25,936 Km/sec
Tale velocità consente al corpo m di proseguire nel suo percorso, ma questa volta la forza di gravità tende ad attirarlo verso il centro della Terra, per cui la sua Energia cinetica diminuisce lungo il tragitto.
Di nuovo l'Energia Totale deve conservarsi.
Per cui il corpo m raggiunge a fatica l'altra estremità del tunnel, ma esaurisce tutta la sua Energia cinetica.
Quando accade questo?
Quando la distanza del corpo m dal centro della Terra diventa uguale a r iniziale (ossia, quando m raggiunge l'altra estremità del tunnel).
Infatti in tali condizioni (identiche a quelle iniziali), l'Energia di potenziale è uguale a quella iniziale:
E pot 0 = GMm/r
dato che r2 è uguale a r
E pot 2 = GMm/r2 = GMm/r = E pot 0
Se Epot2 è uguale a Epot0, dato che l'Energia Totale deve conservarsi, l'Energia cinetica di m non può che essere uguale a zero.
E Totale = E pot 0 + Ec0 = GMm/r + 0
per cui:
E Totale = E pot 2 + Ec2 = GMm/r + 0
Ec2 = 0
A questo punto siamo tornati alle condizioni iniziali e prima di essere acciuffato il corpo m nuovamente cade all'interno del tunnel ed inizia un nuovo ciclo, destinato a ripetersi, sempre che non intervengano altre forze.
Per cui il corpo m acquista energia cinetica spinto dalla forza di gravità fino al punto più vicino al centro della Terra, poi comincia a perderla e inizia nuovamente il suo viaggio di risalita verso l'altra estremità del tunnel, per ricadere nuovo.......
http://www.astrobin.com/full/78662/I/
Visto che é Natale aggiungo anche un'animazione.
http://www.astrobin.com/full/78662/K/
Due piccole questioni finali.
Innanzitutto è facile dimostrare che il corpo m non possiede la necessaria velocità di fuga per uscire dall'altra estremità del tunnel ed abbandonare la Terra.
Infatti, la sua velocità di fuga nel punto più vicino al centro della Terra è maggiore di V1.
La velocità di fuga alla distanza minima è pari a:
vf = (2GM/r1) ^ ½
La relazione per calcolare la velocità di fuga si può ricavare assumendo che l'Energia cinetica sia sufficiente per vincere la Forza di attrazione gravitazionale, diventando zero a distanza infinita.
Ossia m nel punto più vicino al centro della Terra deve possedere un Energia Totale, paria a:
ET = 1/2 m vf ^2 - GMm/r1
Dato che l'Energia Totale di m deve mantenersi e che a distanza infinita tale Energia vale zero, tale relazione diventa:
0 = 1/2 mvf ^2 - GMm/r1
per cui:
1/2 mvf ^2 = GMm/r1
1/2 vf ^2 = GMm/m r1
vf ^2 = 2GM/r1
vf = (2GM/r1) ^ ½
vf = (79,7732 10^13 mt^3/s^2 / 1 10^6 mt) ^ ½
vf = (797,732 10^6 mt^2/s^2 )^ ½ = 28,24 10^3 mt/s = 28,24 Km/s
In pratica in queste condizioni il corpo m non ha alcuna chance di raggiungere la velocità di fuga.
L'ultima questione invece riguarda la traiettoria del corpo m.
In pratica, il problema che riscontro è che se il tunnel passa troppo lontano dal centro della Terra, m rischia di cozzare contro la parete del tunnel ed addio sali e scendi perpetuo, come mostra la figura.
http://www.astrobin.com/full/78662/J/
Spero di averci preso, comunque ne approfitto per fare gli AUGURI a tutti e tutte.
Paolo
caro Paolo,
in un certo senso l'approccio sarebbe anche giusto, ma hai considerato sempre una certa massa M. Sei sicuro? A mano a mano che scendi la massa gravitazionale non è più la stessa... Diciamo che ti sei avvicinato qualitativamente, ma non hai tenuto conto del campo gravitazionale variabile a cui è soggetta la massa m... (almeno così mi sembra...).
Pensaci un po' sopra e vedrai che puoi anche riuscire a spiegare come varia la massa gravitazionale della Terra: è più semplice del previsto...
Ricorda che che, comunque esegui il buco (anche passando dal centro o solo tagliando una fettina), il discorso non cambia...
Buon Natale col ... buco!!!!
Caro Enzo hai ragione, non ho considerato la variazione della massa gravitazionale e comunque ho aggiunto un 2 di troppo al calcolo delle Energie di potenziale (colpa di un mio improprio utilizzo del copia e incolla dei risultati che avevo trovato... ho usato 2GMm/r invece di GMm/r, come correttamente enunciato).
Un errore di impostazione del problema, dato che consideravo, erroneamente, la massa di un corpo solido unico, con la stessa stessa forza di attrazione gravitazionale (ciò è vero all'esterno del corpo, ma non al suo interno).
Potrei anche arrivare a determinare la massa in gioco con un raggio più corto, calcolando volume (V= 4/3 π r^3) e densità media della Terra (densità = Massa/volume), ma il corpo m quando è nel tunnel dovrebbe subire un'attrazione gravitazionale opposta dovuta alla massa tutt'altro che trascurabile presente alla destra del tunnel (nella figura precedentemente postata).
Una massa che assomiglia a un semicerchio..... con quale centro di gravità?
Come vedi ho qualche difficoltà ad identificare le forze gravitazionali in gioco.
Comunque ci penserò.
Paolo
caro Paolo... perfetta l'impostazione. Per risolvere il problema della massa "a destra" ti consiglio di lavorare con le forze relative a volumetti di massa opposti... si può riuscire. Troveresti un teorema abbastanza sconosciuto ma di estrema importanza anche per la relatività...
Comunque, Buone Feste!!!
e questa sarebbe scienza? ma fate più didattica,invece di fare i giochini dei bambini...poveri noi!
caro Giovanni,
vedo che comunque il blog ti piace (visto che sei tornato). Che ne diresti di dare la soluzione alla quale ha lavorato anche un "bambinone" come Newton? Ovviamente con i calcoli necessari a dimostrare il risultato...
Buone Feste
Tentativo numero 2:
Ovviamente, evito di ripetere quanto già detto nel tentativo numero 1, aggiungendo una piccola riflessione di carattere generale (che personalmente trovo essenziale).
Quando uso e trasformo delle relazioni, inserisco sempre le unità di misura delle grandezze fisiche, poiché il risultato deve necessariamente produrre un'unità di misura finale congrua.
In parole semplici, se dopo un passaggio matematico ottengo che una valore di velocità in Kg/sec (ma anche in mt/sec^2), significa che c'è qualcosa che non funzione nei passaggi matematici effettuati.
Prima della caduta nel Tunnel l'Energia cinetica del corpo m è uguale a zero.
Ec0 = 1/2 m v^2 se v=0 Ec0= 0
La sua Energia di Potenziale è:
Epot0 = GMm/r = (6,67 ·10^−11 mt^3/kg s^2 5,98 · 10^24 kg 1 kg) / 6,38 10^6 mt
semplifico le unità di misura:
Epot0 = (6,67 ·10^−11 mt^2/ s^2 5,98 · 10^24 1 kg) / 6,38 10^6
Aggiusto le potenze di 10 del numeratore
Epot0 = (6,67 ·5,98 Kg mt^2/ s^2 10^13) / 6,38 10^6
Aggiusto le potenze di 10 tra numeratore e denominatore
Epot0 = (6,67 ·5,98 Kg mt^2/ s^2 10^7) / 6,38
Eseguo l'operazione:
Epot0 = (39,886 10^7 Kg mt^2/ s^2 ) / 6,38
Epot0 = 6,2518 10^7 Kg mt^2/ s^2 10^7
Epot0 = 62,518 10^6 Kg mt^2/ s^2
Nella posizione più vicino al centro della Terra l'Energia di Potenziale del corpo m è:
Epot1 = GM1m/r1
Il valore di r1 (minima distanza tra Tunnel e centro della Terra), nell'esempio vale 1 10^6 mt, ma la massa M in gioco, ora è minore.
Come calcolare tale valore?
Averi potuto cercare il valore di densità media della Terra in rete, ma preferisco usare solo i dati inseriti nel quiz, per cui: il Volume di una sfera è pari a: Vol = 4/3 π r^3
Il volume della Terra (assimilata ad una sfera, in realtà è una sfera “allungata”) è approssimativamente paria a:
Vol = 4/3 π r^3 = 4,18879 r^3 = 4,18879 (6,38 10^6 mt) ^3
Vol = 4,18879 (259,694 10^18 mt ^3 )
Vol = 1087,8 10^18 mt ^3
La densità media della Terra è pari a:
d = M/Vol = 5,98 ·10^24 kg /1087,8 10^18 mt ^3
d = 5,98 ·10^6 kg /1087,8 mt ^3
d = 5980 ·10^3 kg /1087,8 mt ^3
d = 5,497 10^3 kg / mt ^3
Una volta ricavata la densità media è piuttosto semplice ricavare il valore di M1.
Il volume di una sfera con raggio r1 (1 10^6 mt) è uguale a:
Vol1 = 4/3 π r^3 = 4,18879 (1 10^6 mt) ^3
Vol1 = 4,18879 10^18 mt ^3
Dato che d= Vol/M , per calcolare la massa M1 basta usare la relazione:
M1 = d Vol1 = 5,497 10^3 kg / mt ^3 4,18879 10^18 mt ^3
M1 = 5,497 10^3 kg / mt ^3 4,18879 10^18 mt ^3
M1 = 23,025 10^21 kg
Una volta ricavati i dati mancanti, ora è possibile calcolare il valore dell'Energia di Potenziale del corpo m rispetto al centro della Terra nel suo punto di maggior vicinanza (r1):
Epot1 = GM1m/r1 = (6,67 ·10^−11 mt^3/kg s^2 23,025 10^21 kg 1 Kg) / 1 10^6 mt
Epot1 = (6,67 ·10^−11 23,025 10^21 1 Kg mt^2/kg s^2) / 1 10^6
Epot1 = (6,67 23,025 10^10 1 Kg mt^2/kg s^2) / 1 10^6
Epot1 = (6,67 23,025 10^4 1 Kg mt^2/kg s^2) / 1
Epot1 = (6,67 23,025 10^4 1 Kg mt^2/kg s^2) / 1
Epot1 = 153,576 10^4 1 Kg mt^2/kg s^2
Dato che l'Energia Totale prima della caduta era paria a:
Etot = Epot0 + Ec0 = Epot0
L'Energia Totale deve conservarsi, per cui la differenza tra le due Energie di Potenziale (Epot0 ed Epot1), ora si è trasformata in Energia cinetica del corpo m.
Epot0 – Epot1 = Ec1
Ec1 = 62,518 10^6 Kg mt^2/ s^2 - 153,576 10^4 Kg mt^2/kg s^2
per facilitare l'operazione riscrivo Epot1 come 1,53576 10^6 Kg mt^2/kg s^2
Ec1 = 62,518 10^6 Kg mt^2/ s^2 - 1,53576 10^6 Kg mt^2/kg s^2
Ec1 = 60,982 10^6 Kg mt^2/ s^2
Ec1 (Epot0 – Epot1) è anche uguale a
Ec1 = 1/2 m v1^2
v1^2 = 2 Ec1/m
v1^2 = 2 Ec1/m
v1^2 = 2 (60,982 10^6 Kg mt^2/ s^2 )/1 Kg
v1^2 = 121,96 10^6 mt^2/ s^2
v1= (121,96 10^6 mt^2/ s^2 )^ ½
v1= 11,043 10^3 mt/ s = 11,043 Km/ s
Tale velocità consente all'oggetto m di allontanarsi dal centro della Terra, finché la sua Energia cinetica si esaurisce.
Infatti, ora la forza di gravità, invece di “spingere” “frena” il movimento dell'oggetto m verso l'altra estremità del tunnel
Una volta arrivato all'altra estremità del tunnel, si ricreano le stesse condizioni iniziali, ossia l'oggetto m dista dal centro della Terra un raggio r uguale a quello iniziale (r2=r) e la massa gravitazionale in gioco è di nuovo la stessa (M = M2) .
Dato che L'energia Totale non varia.
Etot = Epot 0 + Ec = Epot0 dato che Ec0 = 0
Se Epot2 = Epot0
Etot = Epot2 + Ec2 = Epot2
per cui Ec2 =0
A questo punto il corpo m, esaurita la sua energia cinetica viene attratto nuovamente dalla Terra e ricade nel Tunnel, dando vita ad una serie perpetua di andate e ritorni attraverso il tunnel (finché non agiscono altre forze).
Per ora mi fermo qui, ma rimangono irrisolte due questioni essenziali: la traiettoria del corpo m e come considerare l'attrazione gravitazionale esercitata da quella che chiamavo massa a destra (in realtà la massa è tutto intorno ad m, visto che siamo in un Tunnel e che le dimensioni spaziali sono tre e non due).
Sulle risposte ci sto riflettendo ed ho un'idea che tira in ballo Forze e vettori (solo che non conosco minimamente lo sconosciuto teorema di cui parlava Enzo).
Paolo
Sorry , prima racconto di controllare le unità di misura e poi lascio un kg di troppo, che ora ho tolto:
, prima racconto di controllare le unità di misura e poi lascio un kg di troppo, che ora ho tolto:
Epot1 = GM1m/r1 = (6,67 ·10^−11 mt^3/kg s^2 23,025 10^21 kg 1 Kg) / 1 10^6 mt
Epot1 = (6,67 ·10^−11 23,025 10^21 1 Kg mt^2/ s^2) / 1 10^6
Epot1 = (6,67 23,025 10^10 1 Kg mt^2/ s^2) / 1 10^6
Epot1 = (6,67 23,025 10^4 Kg mt^2/s^2) / 1
Epot1 = (6,67 23,025 10^4 Kg mt^2/ s^2) / 1
Epot1 = 153,576 10^4 Kg mt^2/ s^2
Dato che l'Energia Totale prima della caduta era paria a:
Etot = Epot0 + Ec0 = Epot0
L'Energia Totale deve conservarsi, per cui la differenza tra le due Energie di Potenziale (Epot0 ed Epot1), ora si è trasformata in Energia cinetica del corpo m.
Epot0 – Epot1 = Ec1
Ec1 = 62,518 10^6 Kg mt^2/ s^2 - 153,576 10^4 Kg mt^2/ s^2
per facilitare l'operazione riscrivo Epot1 come 1,53576 10^6 Kg mt^2/ s^2
Ec1 = 62,518 10^6 Kg mt^2/ s^2 - 1,53576 10^6 Kg mt^2/s^2
Ec1 = 60,982 10^6 Kg mt^2/ s^2
Ec1 = 62,518 10^6 Kg mt^2/ s^2 - 153,576 10^4 Kg mt^2/ s^2
per facilitare l'operazione riscrivo Epot1 come 1,53576 10^6 Kg mt^2/ s^2
Ec1 = 62,518 10^6 Kg mt^2/ s^2 - 1,53576 10^6 Kg mt^2/s^2
Ec1 = 60,982 10^6 Kg mt^2/ s^2
Paolo
caro Paolo,
tre appunti generali...
1) dici, tra l'altro, che stai attento alle unità di misura e come esempio fai m/sec^2. Beh... non è certo sbagliata, dato che si riferisce all'accelerazione...
2) stai cercando di andare per punti. Tuttavia hai già accettato un legame tra raggio e massa attraente, anche se non l'hai ancora dimostrato (caso del punto più centrale). Potresti cercare di scrivere una formula che leghi le varie quantità e non calcolare la situazione per punti particolari... Posso dirti subito che è però molto semplice ragionare in termini di equazione del moto, dato che salta all'occhio un moto molto particolare. Lavorando solo sull'energia non so se si riesce ad arrivare alla conclusione generale (devo provarci...). Pensa molto al ... pendolo e al suo moto...
Per avere dati confrontabili con la realtà dovresti provare a vedere quanto tempo impieghi ad arrivare al centro (o meglio nel punto più vicino al centro). Se ti viene "circa" 21 minuti... sei sulla buona strada.
3) Puoi trovare difficoltà proprio perché non hai molta esperienza con le leggi del moto (che però, in questo caso, deriva immediatamente tra l'uguaglianza delle forze in gioco...). In altre parole trovare come varia la x del punto P in funzione del tempo (comparirà un'accelerazione che è solo una derivata seconda di x...). Tuttavia, sei sicuramente in grado di dimostrare il teorema misterioso, proprio quello che ti dice che l'unica massa che conta è quella di raggio r, punto per punto, durante tutta la caduta... Mettiti nel punto qualsiasi e cerca di prendere pezzetti di massa (volume) opposti. Se riesci a dimostrare che le forze esercitate da loro si annullano, puoi concludere, senza integrali vari, che la somma delle forze di tutti questi volumetti (a due a due) sul punto si annullano e, quindi, che l'unica massa che si sente è quella "interna"...
Acci, adesso Alvy copia tutto....
caro Paolo,
posso darti un consiglio su cosa impegnarti in questo problema? Innanzitutto, quello che ti ho detto (un po' di geometria e trigonometria facile facile) e poi potresti tracciare come varia l'accelerazione di gravità partendo dal centro della Terra e andare all'infinito... E' un qualcosa che può diventare molto utile in tanti problemi di meccanica classica. Temo che un'equazione del moto ti dia ancora qualche problema (può darsi che sbagli, ovviamente). Però, prova pure con l'energia, ma cercando la formula generale e non andare per punti... insomma cercare cosa si elimina e come si semplificano certe cose... (il volume , come hai detto bene tu) ti permette di eliminare cose importanti... Non per niente abbiamo posto la densità costante!
Scusami se traggo conclusioni personali, ma penso di avere intuito un po' i tuoi punti ancora critici... E' solo questione di tempo, però...
No no Enzo, voglio giocare pulito!
Lo so...lo so (ma da te pretendo l'equazione differenziale!!!!!)
ops... me lo avevi già mandato Alvy... che testa!
me lo avevi già mandato Alvy... che testa! 
Ma no, non ti preoccupare .... è l'età ......
Caro Enzo, fai bene a far emergere le criticità....
Le criticità vanno prima comprese se si vuole provare a superarle (come dicevo all'inizio i quiz servono anche a questo).
Ho anche trovato una relazione che lega il variare dell'accelerazione nel tempo in funzione del variare del raggio.... ma ne ho ancora di strada da percorrere.
Solo una piccola precisazione sulle unità di misura, penso di esser stato frainteso.
So bene che m/sec^2 è l'unità di misura dell'accelerazione (che rappresenta la variazione della velocità nel tempo), ma se in un'equazione sto cercando il valore di una velocità ed alla fine ottengo un risultato in m/sec^2 (ossia il valore di un'accelerazione) invece che m/sec, significa che ho sbagliato qualcosa.
Paolo
scusa Paolo... avevo capito male...

la relazione con l'accelerazione è invece MOLTO interessante
mi spiace caro Enzo ma io proprio non ci arrivo...
Io semplicemente avrei rilevato, come in alcuni articoli passati, che la forza attrattiva era
F = GMm/r^2
la forza con cui un corpo cade era
F= ma
Ponendole a zero avevo GMm/r^2= ma con cui ricavavo che a (accellerazione) = GM/ r^2
Da qui scoprivo che se il corpo inizialmente era fermo cadeva verso il centro con una forza di accellerazione positiva fino a raggiungerlo e, visto che l'equazione è simmetrica, superato il centro la ragnatela gravitazionale avrebbe prodotto una decellerazione (anzichè un'accellerazione) che ne avrebbe ridotto la velocità.
Poi al massimo avrei cercato di porre una condizione in cui, quando l'accellerazione è nulla, lo è anche la velocità di caduta in modo da creare un moto perpetuo di caduta e risalita dell'oggetto di massa m (allacciandomi magari alla formula della velocità cinetica che ci hai fatto vedere F = 1/2 mv^2)
Vedendo però tutti i calcoli che fate credo proprio che sono lontano anni luce dalla soluzione...
Caro Alex, .
.
il problema non sono le formule (sono proprio quelle che riporti tu), ma il descrivere la massa che attrae punto dopo punto la massa in "caduta". Puoi anche pensare alla conservazione dell'energia per capire il concetto, ma per trovare il tempo bisogna valutare come varia la distanza in funzione del tempo (legge del moto)... Dai, ancora pochi giorni e do la soluzione che però penso che tu abbia giustamente intravisto...
Come già detto, pensa al pendolo... non abbatterti e abbastanza complicato proprio per quest'ultima considerazione
Per logica e pensando al pendolo, come si dice nell'articolo, mi viene da pensare che l'oggetto che viene lasciato cadere nel buco continui ad oscillare all'infinito.
Questo perchè l'oggetto subirà un'accelerazione fino al centro della terra, poi continuerà la sua corsa verso l'uscita. Questa corsa però verrà rallentata dall'attrazione gravitazionale esercitata dal nucleo della terra, che a sua volta porterà l'oggetto a ricadere verso il centro, in una corsa senza fine (considerando l'assenza totale di attrito)...
Spero di non aver scritto una castroneria.
PS: i calcoli non sono il mio forte
Un aiutino per chi vuole fare i calcoli: la massa dello spicchio sopra il treno non conta perché controbilanciata da quella opposta. quindi per il calcolo dell'accelerazione istantanea conta la distanza dal centro della sfera.
Caro Enzo, so che hai pubblicato la soluzione che mi leggerò con calma.
Però vorrei esporre quanto avevo trovato (legame tra raggio ed accelerazione), soprattutto per capire se e quali errori ho commesso.
Nell'affrontare il problema, mi sono arenato sul calcolo di tempi e velocità, per cui spero che la soluzione fornisca risposte ai miei dubbi (tieni conto che l'articolo sulle derivate le ho solo lette frettolosamente, e che la derivata seconda ancora non l'ho letta e mi ero ripromesso di studiarle a fondo... ).
).
Nel suo viaggio all'interno del Tunnel, l'accelerazione a cui è sottoposto il corpo m cambia continuamente, insieme al raggio r ed alla Massa M in gioco.
F= ma
a = F/m
La Forza di gravità a cui è sottoposto il copro m è uguale a.
F = GMm/r^2
per cui l'accelerazione è uguale a:
a= GMm/mr^2 = GM/r^2
Ma all'interno della Terra, M varia nel tempo, così come r e l'accelerazione.
La Massa, è uguale alla densità per il suo volume.
M = den Vol
Il volume di una sfera è pari a:
Vol = 4/3 π r^3
Quindi:
a= G (den 4/3 π ) r^3/r^2
a= (G den 4/3 π) r
G, 4/3 π e la densità sono costanti (la densità media viene per condizione posta come costante), per cui può ridefinire come K
K= (G den 4/3 π)
Il suo valore è semplice da stabilire, dato che la densità della Terra era già stata calcolata:
Vol terra = 4/3 π r^3 = 4/3 π (6,38 10^6 mt)^3 = 4/3 π 259,694072 10^18 mt^3
Vol terra = 1087,80 10^18 mt^3
La sua densità media è quindi pari a:
den = M/Vol = 5,98 10^24 kg / 1087,80 10^18 mt^3
den = 5,4973 10^3 kg/mt^3
Sostituendo i valori trovati:
K= (G den 4/3 π) = ( 6.67 ·10^−11 mt^3/kg s^2) (5,4973 10^3 kg/mt^3) 4/3 π =
K= ( 6.67 ·10^−8 /s^2) (5,4973 ) 4/3 π
K= 153,590 10^−8 /s^2
a= (G den 4/3 π) r = K r = (153,590 10^−8 /s^2) r
Questa relazione consente di ottenere il valore del raggio corrispondente all'accelerazione a cui m è sottoposto in un dati istante di tempo e viceversa, tenendo conto della riduzione della Massa che esercita la forza di gravità.
Se funziona deve consentire di calcolare le varie accelerazioni punto per punto, del percorso del corpo m, in rapporto al raggio.
Con raggio uguale a zero (anche se il raggio si riduce a zero, in tale raggio non può essere contenuta alcuna massa.... siamo sulla Terra e in un buco nero).
a= K r = (153,590 10^−8 /s^2) 0 mt = 0
Con raggio pari a 1 10^6 mt
a1= K r = (153,590 10^−8 /s^2) 1 10^6 mt = 153,590 10^−2 mt/s^2 = 1,53590 mt/s^2
In superficie (appena viene lasciata cadere):
a1= K r = (153,590 10^−8 /s^2) 6,38 10^6 mt = 979,904 10^2 mt/s^2 = 9,79904 mt/s^2
Direi che coincide con quella classicamente conosciuta da noi superficicoli (abitanti della superficie).
Invece, per un corpo che si allontana dalla Terra, dato che è al suo esterno, la massa della Terra rimane ovviamente costante, a variare è la distanza tra il corpo in allontanamento ed il centro della Terra, per cui si utilizza la classica formula:
a= G M/r^2
La relazione precedentemente trovata (a= G (den 4/3 π ) rt^3/r^2 ) complica solo le cose, poiché il raggio contenuto al numeratore è quello della Terra (rt), mentre quello al denominatore rappresenta la distanza tra m ed il centro della Terra
Quando il corpo in allontanamento dista 1 10^6 mt dalla superficie terrestre (1.000 Km), lo stesso dista 6,38 10^6 mt + 1 10^6 mt = 7,38 10^6 mt
a= G M/r^2= (6,67 ·10^−11 mt^3/kg s^2 ) ( 5.98 · 1024 kg )/ (7,38 10^6 mt) ^2
a= (39,8866 · 1013 mt^3/ s^2)/ 54,4644 10^12 mt ^2
a= 7,32379 mt/ s^2
All'infinito:
a= G M/r^2= G M/r^2 = 39,8866 10^13 · mt^3/ s^2 / (∞ mt ) ^2 = 0
Il nostro corpo m però non corre il rischio di allontanarsi dalla Terra.
L'energia Totale posseduta dal corpo m prima di cadere era uguale a
E tot = Epot0 + Ec0
Dato che all'inizio il corpo m è fermo Ec = 0
Se l'Energia Totale si deve conservare, significa che in un qualunque punto del percorso di m, questa deve essere uguale a quella iniziale, ossia Epot0
Epot0 = Epot1 + Ec1
Ec1 =Epot0 - Epot1
L'energia di potenziale è uguale a:
Epot = GMm/r sostituendo alla Massa quanto trovato prima:
Epot = (G den 4/3 π ) m r^3/r dato che K= (G den 4/3 π)
Epot = K m r^2 =
Per cui:
Etot = Epoto = K m r^2
Epot 1 = K m r1^2 ovviamente il raggio è diverso da r iniziale
Ec1 =Epot0 - Epot1 =K m r^2 - K m r1^2
Ec1 = K m (r^2 - r1^2 )
E' del tutto evidente che quando r1 è uguale a r, l'Energia cinetica diventa uguale a zero, per cui il corpo m una volta arrivato dall'altra parte del tunnel ricade immediatamente, ricominciando tutto da capo. Più r1 è piccolo, più aumenta l'Energia cinetica.
Mi fermo qui anche se ho proseguito cercando di affrontare il problema della velocità, dato che lo spazio percorso in un certo tempo da m non è uguale al raggio (a parte il caso in cui il Tunnel passa proprio per il centro della Terra)......
Una prima visione geometrica del problema sembra legare lo spazio al coseno del raggio....
Ora vado a leggermi l'articolo.
Paolo
caro Paolo,
tu dici cose giuste... quello che non riesco a vedere è la risposta al quiz. Quanto tempo impiega, ad esempio? Tuttavia, hai scritto l'equazione esatta e i concetti sono OK. Dovresti poterlo calcolare anche tu... dimmi qualcosa...
Beh adesso che ho letto la prima parte della soluzione, sarebbe troppo facile, solo che io mi ero arenato (urge lettura derivate).
Diciamo che usando il Periodo P io avrei trovato:
ω = (K)^1/2
dato che nei mei cacoli k vale GMT/r^3 r è quello della Terra, per cui è anch'esso costante.
Per cui:
P = 2π/ω = 2π/ (K)^1/2,5
P = 2π/ ( 153,590 10^−8 /s^2)^1/2 = 2π/ 1,239 10^-3 = 5071 secondi = 84,51 minuti
Ora Un Periodo è pari ad un nadta e ritorno, per cui il corpo m inpiega un tempo pari ad 1/4 di P
P= 5071 sec/4 = 1267 secondi = 21 minuti e 7 secondi.
Paolo
PS: Scusa Enzo, ma nella tua formula finale della soluzione, mi sa che hai invertito (GMT/R^3)^1/2:
P = 2π/ω = 2π/(R3/GMT)1/2
caro Paolo,
hai ragione! mi era scappata una barra in più (avevo già invertito omega...). Predico bene e razzolo male
Come vedi... eri proprio a un passo dalla conclusione!!!!