Questo articolo è inserito nella sezione d'archivio "Ottica"

 

Abbiamo parlato tanto di fotoni e di meccanica quantistica che le onde elettromagnetiche non possono certo farci del male. Inoltre, la polarizzazione, insieme ai neutrini primordiali, potrebbero essere le informazioni decisive per raggiungere il Big Bang o chi ne fa le veci.

Mettiamo subito i puntini sulle “i”. Innanzitutto, sappiamo benissimo che la luce si propaga attraverso onde. Che poi queste onde possano collassare in una particella è affare della meccanica quantistica. Noi ci limitiamo a parlare di onde, sapendo che non commettiamo nessun errore. , sappiamo anche molto bene che la radiazione elettromagnetica è formata da un’onda elettrica e da una magnetica che oscillano su due piani che sono sempre perpendicolari tra loro. Ragione per cui, permettetemi di considerare solo la parte elettrica, tanto l’altra è costretta a seguirla come un cagnolino. Infine, cosa decisamente molto importante anche se meno intuitiva, sarebbe molto meglio definire un’onda elettrica come un’oscillazione di un campo elettrico.

Un campo, in generale, è associato a una forza. Prendiamo il caso più consueto del campo gravitazionale, legato alla forza gravitazionale. Se inseriamo una certa massa M in un certo punto dello spazio, essa esercita su tutti gli oggetti che le sono attorno una forza che varia a seconda della distanza e della massa m dell’oggetto che la subisce. La distribuzione delle forze agenti nello spazio attorno a M viene rappresentata molto bene da una specie di mappa che associa a ogni punto dello spazio la forza corrispondente. Cosa sia un vettore ormai lo sappiamo molto bene (chi non lo sa o vuole solo rinfrescare la memoria, può trovare tutte le spiegazioni in questo articolo)

Nel campo, sarebbe ancora meglio sbarazzarsi della massa m dell’oggetto (dato che cambia da oggetto a oggetto). Avremmo così una mappa che vale indipendentemente dall’oggetto. Facilissimo: basta dividere la forza per la massa m, ossia considerare la forza per unità di massa (in pratica otteniamo l’accelerazione di gravità). Questo nuovo vettore non dipende più dalla massa m dell’oggetto, ma indica benissimo come agisce la forza di gravità tutt’attorno alla massa M. La nuova mappa prende il nome di campo gravitazionale (la nostra famosa "ragnatela"spiegata in questo articolo – fig. 7).  Possiamo, perciò, concludere che un campo gravitazionale è descritto perfettamente da un vettore.

Nel caso del campo elettrico, il vettore è definito dalla forza elettrica  divisa per la carica elettrica, in modo analogo a quello che succede per la forza gravitazionale. Attenzione a non confondere una carica elettrica con il campo elettrico da lei generato. E’ come se confondessimo una massa M con la forza gravitazionale. In questo articolo, però, noi ci occupiamo della propagazione del campo elettrico. La propagazione del campo gravitazionale è ancora un problema aperto, soprattutto perché non è ancora stata trovata la particella mediatrice (per la luce è il fotone).

Ricordiamo, invece, che le onde gravitazionali sono previste dalla teoria della relatività e descrivono la deformazione dello Spazio-Tempo, dovuta ad accelerazioni di grandi masse o, più in generale, alla deformazione continua di una massa (il famoso momento di quadrupolo non nullo). Le onde gravitazionali si propagano contraendo ed espandendo ritmicamente lo Spazio-Tempo. Ma, adesso, torniamo a “bomba”.

Da quanto detto finora è, quindi, possibile rappresentare il campo elettrico come un vettore che ha un certo modulo, una certa direzione e un certo verso. Il dire che luce si propaga, vuole dire che il vettore campo elettrico si muove lungo una certa direzione. Chi oscilla allora? Proprio il campo elettrico che rimane, però, sempre perpendicolare alla direzione del moto. La combinazione del moto di oscillazione e di traslazione rettilinea (la luce viaggia in modo rettilineo se nessuna massa la viene a disturbare) dà luogo alla ben nota onda luminosa. Immaginate una pallina che continui a rimbalzare su un tavolo, mentre il tavolo si sposta di moto rettilineo.

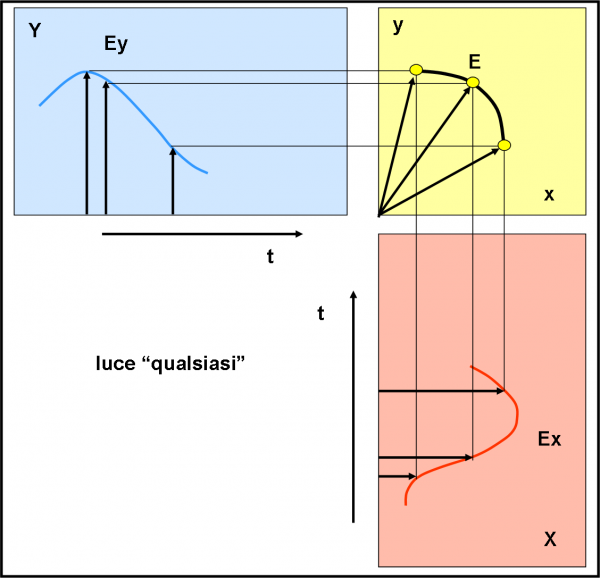
Vediamo tutto ciò in Fig. 3, dove il campo elettrico ha la massima intensità in un certo verso, poi si riduce a zero e quindi cambia di verso raggiungendo di nuovo un massimo. Non prendiamo, però, questa figura come un dato di fatto. L’oscillazione deve sicuramente avvenire in una direzione perpendicolare alla direzione di propagazione, ma NON è detto che lo faccia sempre su un solo piano.

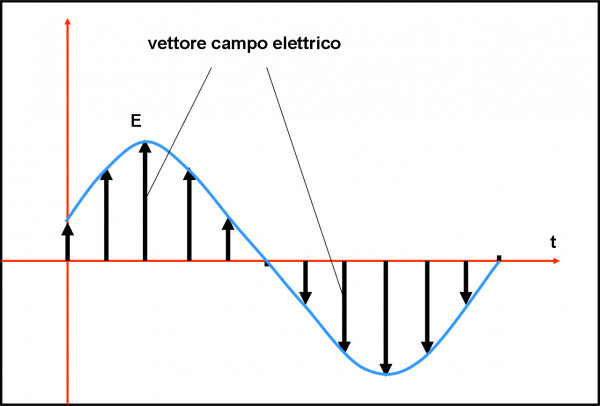
Data una retta, infatti, esistono infinite direzioni perpendicolari alla retta, ossia tutte quelle che giacciono sul piano perpendicolare alla retta, come mostrato in Fig. 4, e quindi anche infiniti piani in cui può propagarsi l’onda. Nei casi reali il vettore del campo elettrico può effettivamente avere qualsiasi direzione e, quindi, anche il piano in cui oscilla il vettore può essere qualsiasi e può variare nel tempo. La sorgente di luce, normalmente, non si cura di come oscillano le onde che ha generato. Anzi, normalmente, la luce emessa si propaga in modo del tutto disordinato e senza nessuna regola, a parte quella di mantenere l’oscillazione del vettore campo elettrico perpendicolare alla direzione di propagazione.

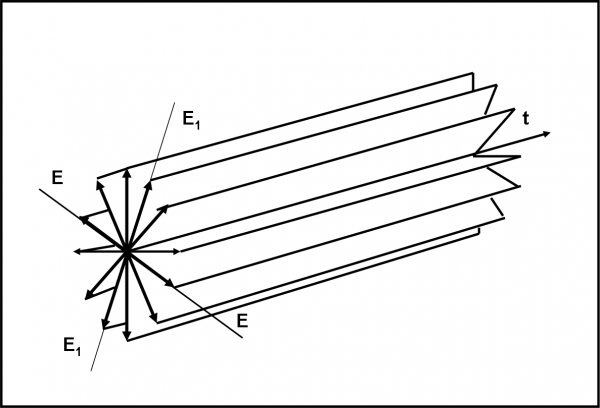
Un ottimo metodo per descrivere abbastanza bene come si propaga la luce è quello di fissare due piani di riferimento e osservare la proiezione su di essi dell’onda descritta dal campo elettrico (Fig. 5). Se la luce è quella normale, vedremmo un caos terribile. Se invece l’andamento su questi due piani acquista caratteristiche regolari, potremmo capire se alla luce sta succedendo qualcosa di speciale e riuscire a darle una descrizione logica in termini delle grandezze che caratterizzano l’onda.  Quel qualcosa di speciale è proprio la polarizzazione.

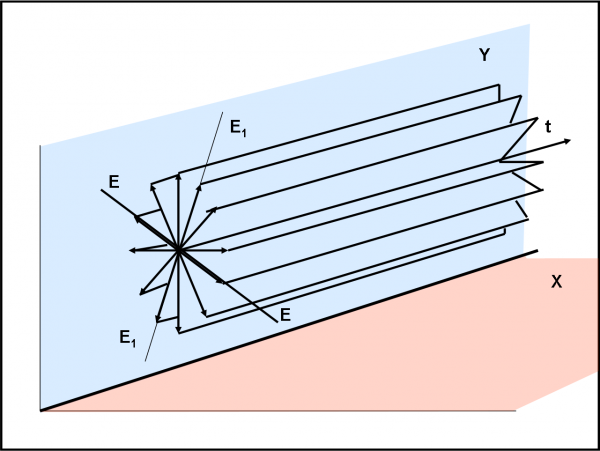
Il succo del discorso è del tutto simile al caso in cui abbiamo un vettore su un piano x,y. Se quel vettore cambia continuamente, lo fanno anche le sue componenti sugli assi x e y. Ma se la direzione e l’intensità del vettore sono sempre le stesse o se si muove con regolarità, le sue componenti mostreranno caratteristiche più o meno regolari.  Ad esempio, se un vettore si muove lungo una direzione fissa e ha sempre la stesso modulo, le sue componenti si mantengono costanti. Se, invece, il vettore ruota attorno a un punto, le componenti passano da un valore massimo a uno minimo e poi di nuovo a un massimo, in modo periodico. Se il vettore è parallelo all’asse x, la componente sull’asse y è sempre zero, e via dicendo…

Ebbene, noi non facciamo altro che proiettare tutta l’onda su due piani scelti come piani di riferimento e perpendicolari tra loro. A seconda di come si comportano queste due onde proiettate si può capire cosa fa quella reale. Vi sono vari tipi di polarizzazione e cerchiamo di capirli attraverso le proiezioni del movimento del vettore campo elettrico sui due piani perpendicolari tra loro.

Disegniamo la Fig. 6 che è in tre dimensioni. Sono rappresentati i due piani ortogonali X (rosso) e Y (azzurro), in cui giacciono le proiezioni dell’onda e la direzione di propagazione del campo (ossia l’asse del tempo). In ogni piano abbiamo un’onda come quella di Fig. 3, solo che in questo caso la singola onda è descritta dalla componente del vettore campo. Il campo E, istante per istante, individua una componente Ex e una Ey sui due piani X e Y. Sono queste due componenti che descrivono le due onde. A causa dell’oscillazione del vettore E, anche le componenti oscillano, assumendo, ovviamente, valori sia positivi che negativi. In altre parole, istante per istante, il vettore E si scompone nelle sue due componenti nel piano definito dagli assi x e y, appartenenti  rispettivamente ai piani X e Y. Questo piano (giallo) è, per costruzione, perpendicolare alla direzione del moto.

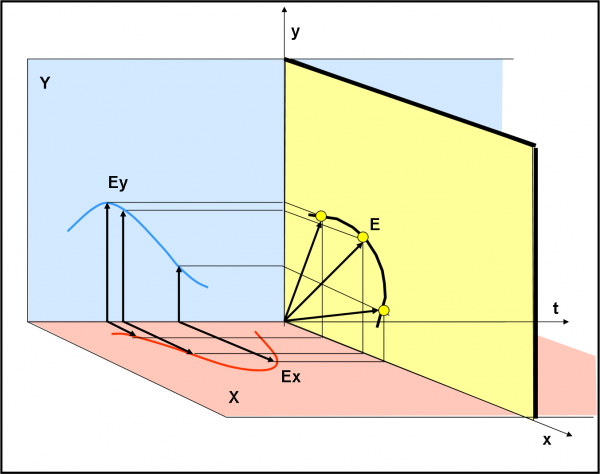
E’ come se tagliassimo istante per istante la figura e guardassimo cosa capita sui due piani X e Y. Anzi facciamo di meglio: tutto ciò che capita negli infiniti piani gialli lo proiettiamo su uno solo di coordinate cartesiane x e y. Per ogni piano abbiamo le due componenti del vettore E e, quindi, da loro, è facile costruire il vettore E istante per istante sul piano giallo (date due componenti si ricava subito il vettore). A seconda di come si comporta questo vettore sul piano, definiamo se e come la luce è polarizzata. Ovviamente, ci conviene “lavorare” sui due piani X e Y, trafficando con le due onde proiettate e vedere come le loro caratteristiche si riflettono sull’andamento del campo elettrico totale. Ho sprecato un mucchio di parole, ma penso che la visione della figura sia molto più utile e semplice.

Teniamo ben presente che l’uso dei due piani perpendicolari è di interesse pratico per capire e/o agire. La propagazione della luce non conosce i due piani perpendicolari, ma sa solo che può variare, istante per istante, la direzione, l’intensità e il verso del vettore campo elettrico, con l’unico obbligo di essere perpendicolare alla direzione di propagazione. E’ il vettore l’unica entità fisica che determina la polarizzazione. Il nostro approccio ha solo un valore descrittivo da un lato, ma, dall’altro, permette anche di sapere come intervenire se si volesse polarizzare la luce. Comunque, non esageriamo… cosa siano i polarimetri e come la luce venga polarizzata va oltre lo scopo di questo articolo. Basti dire che bastano un paio di occhiali polaroid per intervenire direttamente, oppure una riflessione, una dispersione o una contrazione e dilatazione dello Spazio-Tempo per causare una polarizzazione naturale. A buon intenditor poche parole… magari ci torniamo alla fine.

Va bene, passiamo a descrivere i tre tipi di polarizzazione fondamentali utilizzando una piccola variazione della Fig. 6, rendendola più gestibile, abbandonando le rappresentazioni tridimensionali che sono sempre difficili da disegnare. Cerchiamo, quindi, di “aprire” quella figura e distenderla sul piano del foglio.

Il piano azzurro (Y)  lo lasciamo com’è. L’asse del tempo è quindi orizzontale e va verso destra. Adesso, prendiamo il piano X (rosso), lo ruotiamo di 90° verso il piano del foglio (in tal modo viene a coincidere con lui) e poi ancora di 90° in senso antiorario. Otteniamo il piano rosso di Fig. 7. Il suo asse del tempo è, adesso, diretto verso l’alto ed è, ovviamente, perpendicolare a quello del piano Y. Poi, prendiamo il piano giallo e lo ruotiamo in senso antiorario attorno all’asse che ho indicato con y (l’intersezione tra piano azzurro e piano giallo originario). Anche il piano giallo si deposita sul piano del foglio. E’ proprio come se avessimo aperto la “scatola” della Fig. 6. Studiateci un po’ sopra e vedrete che abbiamo operato una trasformazione piuttosto semplice. Qual è il grande vantaggio di questa rappresentazione? Innanzitutto, abbiamo tutto sul piano del foglio. Ma, ancora più importante, per ogni istante t, possiamo tranquillamente proiettare le componenti del campo elettrico del piano azzurro e del piano rosso sul piano giallo attraverso rette parallele ai rispettivi assi del tempo. Dove queste rette (corrispondenti a istanti uguali, mi raccomando) si incontrano, otteniamo immediatamente il vettore E, con tanto di direzione, intensità e verso. La curva nera sul piano giallo descrive la variazione del campo elettrico. In parole molto povere, dalle due componenti sugli assi x e y otteniamo il vettore campo.

Non spaventatevi e guardate con attenzione le Fig. 6 e 7.  Vedrete che sanno spiegare la faccenda meglio di tante parole. La geometria è il linguaggio migliore e più sintetico per spiegare i movimenti di grandezze fisiche. La matematica descrive i concetti, la geometria descrive le situazioni e i moti. Due linguaggi che si danno del tu! Cerchiamo di usarle più che possiamo… solo loro ci permettono di descrivere perfettamente i fenomeni fisici.

Compresa la Fig. 7,  possiamo utilizzarla per descrivere qualcosa di più interessante di quella curva nera che non significa niente e che ho costruito andando a casaccio.

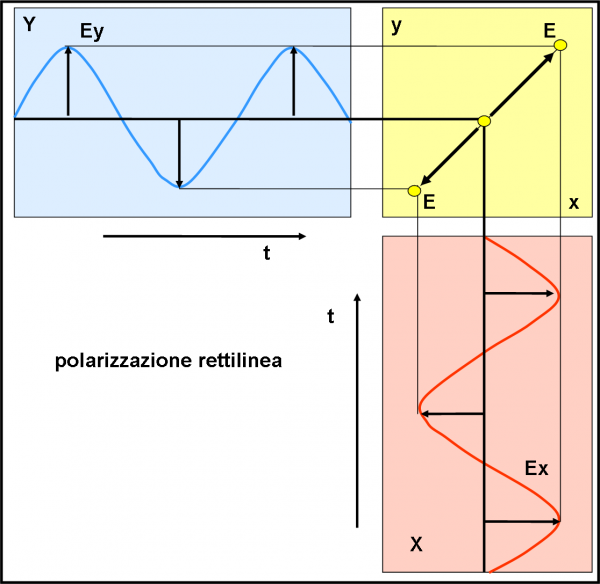
Cominciamo con la Fig. 8. Come già detto, lavoriamo sulle onde proiettate nei piani rosso e azzurro. Consideriamo due onde che abbiano la stessa frequenza (o la stessa lunghezza d’onda) e la stessa ampiezza (vedremo che possiamo farlo senza grossi problemi), e che siano perfettamente in fase. Questo vuol dire che quando la prima è al minimo lo è anche la seconda e via dicendo; ossia, si mantengono non solo uguali tra loro ma viaggiano anche di conserva. Scegliamo qualche punto particolare della prima e quelli corrispondenti della seconda. Tracciamo le rette parallele agli assi del tempo fino a farle incontrare nel piano giallo. Ogni punto giallo determina il vettore campo totale. In questo caso particolarissimo il vettore risultante si muove costantemente nella direzione EE, accorciandosi, allungandosi e cambiando verso. Oscillando, insomma. Cosa significa tutto ciò? Solo e soltanto che il vettore campo oscilla su un solo piano, sempre lo stesso, la cui intersezione con il piano giallo è proprio la retta EE. Non solo, ma il piano è inclinato di 45° rispetto a quelli rosso e azzurro (dato che in ogni punto la x è uguale alla y… ricordate la retta y = x?).

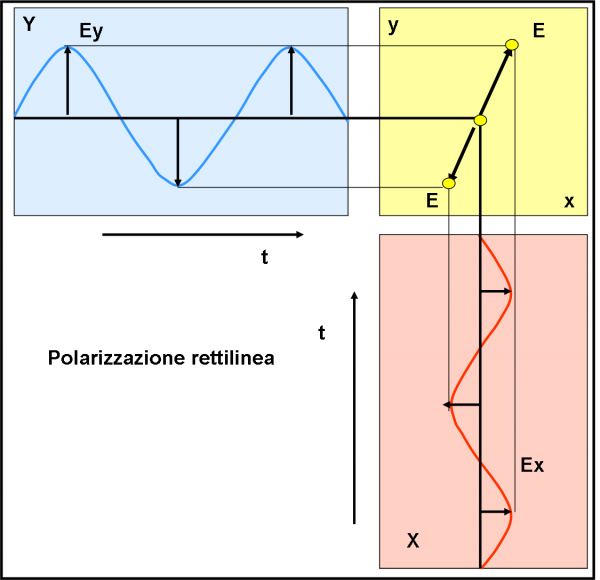
Se cambiamo le ampiezze, mantenendo, però, la stessa fase, otteniamo ciò che vediamo nella Fig. 9. Il vettore campo totale oscilla sempre su un unico piano, ma la sua inclinazione cambia (è come se moltiplicassi la x per un fattore maggiore o minore di 1, ossia y = mx).

Se, invece sfasiamo le due onde di 180° (π), ossia se al massimo di una curva facciamo coincidere il minimo dell’altra, otteniamo la Fig 10. Abbiamo ottenuto un ribaltamento della retta intersezione del piano giallo, ossia del piano di oscillazione del campo (y = -x).

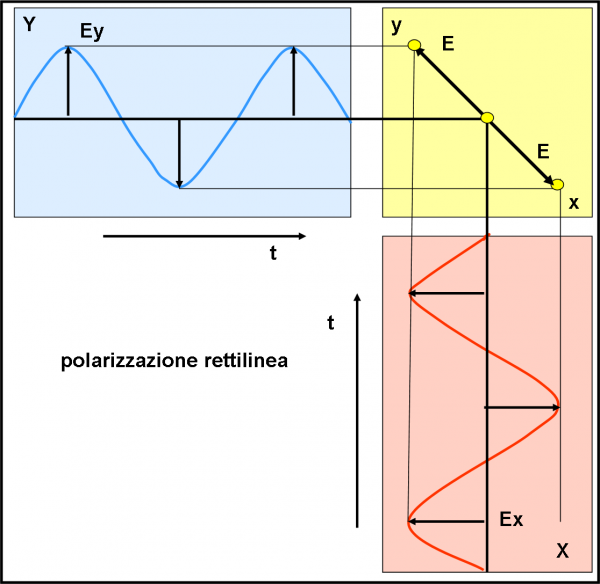
Non vi stupite di certo se vi dico che otterrei lo stesso risultato, mantenendo immutata la fase e facendo variare l’ampiezza dell’onda rossa. Pensate solo che variando l’ampiezza passerei per ampiezza nulla (il piano di oscillazione finale sarebbe quello azzurro dato che non vi è nessun’onda nel piano rosso) e poi andrei verso il basso, ossia ribalterei l’onda rossa, che vuole proprio dire averla sfasata di 180° rispetto a quella azzurra.  Vi invito a divertirvi un po’ facendo variare le ampiezze: vedrete proprio che la retta EE continua a fare "girotondo" sul piano giallo. In ogni caso però, sia che si considerino ampiezze diverse, sia che si sfasi l’onda di 180°, continuiamo ad avere un’onda che giace su un solo piano, più o meno inclinato. O -se preferite- Il vettore oscilla sempre su questo piano.

Siamo nel caso della polarizzazione rettilinea e il piano in cui avviene l’oscillazione è detto piano di polarizzazione.  Come si potrebbe fare per determinare, praticamente, questo piano? Basterebbe avere un filtro speciale che bloccasse la luce che è polarizzata secondo un piano. Facendolo girare, quando il piano “proibito” dello strumento coincide con quello di polarizzazione della luce non si vedrebbe più niente, dato che tutta la luce che giunge a noi lo fa solo oscillando su quel piano. Se, invece, lo strumento fosse in grado di fare passare la luce solo se oscilla su un piano, diventerebbe un magnifico polarizzatore della luce. Gli occhiali da sole “polaroid” fanno proprio quest’ultima operazione (più o meno…). Infatti, provate a metterveli e poi prendete un altro paio di occhiali identici e girateli di 90° rispetto ai primi. Non vedreste praticamente più niente! La luce che fa passare il primo paio sarebbe bloccata dal secondo!

Torniamo alla nostra geometria… descrittiva e complichiamo un poco le cose.  Ci basta sfasare le due curve rossa e azzurra di 90° (π/2): dove una ha un massimo o un minimo, l’altra deve essere uguale a zero. Rappresentiamo questa configurazione nella Fig. 11. prendiamo alcuni punti particolari (massimi, minimi e punti zero) della prima e quelli corrispondenti della seconda (a parità di tempo, mi raccomando!). Prolungando tutto sul piano giallo otteniamo i quattro punti gialli. Aggiungiamo anche un punto verde, scelto per un istante intermedio. Non è difficile concludere che il vettore campo continua a ruotare attorno alla direzione di propagazione e che quindi oscilla su un piano che ruota costantemente attorno all’asse del tempo. Il vettore campo, durante il movimento, descrive una circonferenza e la polarizzazione diventa circolare. Cosa succede se una delle due onde varia di ampiezza? La circonferenza diventa un ellisse ma mantiene i semiassi lungo le direzioni x e y. Provate…

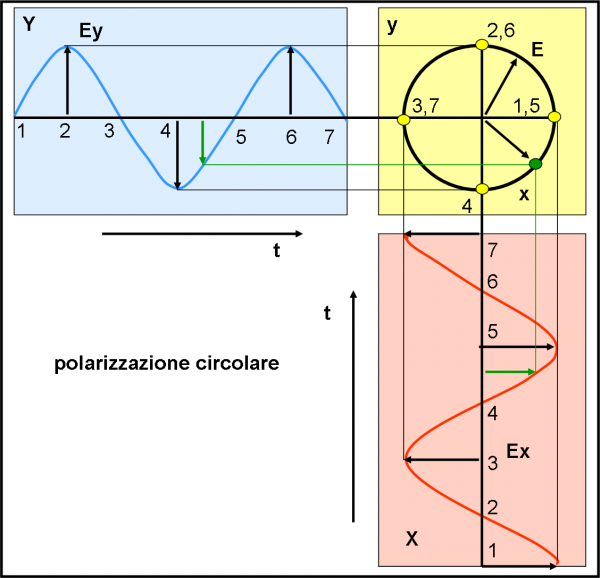
E’ più istruttivo rappresentare l’ultima configurazione, quella meno “particolare”. Le due curve sono sempre uguali, ma sfasate di un angolo qualsiasi. Facciamone un esempio in Fig.12. Oltre che i punti gialli, ho preso molti punti verdi intermedi in modo da capire meglio cosa succede. Il vettore campo descrive un’ellisse con gli assi inclinati rispetto agli assi x e y. La luce è ancora polarizzata, ma ellitticamente. Lascio a voi pensare a cosa capita se diminuisco una delle due ampiezze… E’ ormai banale.

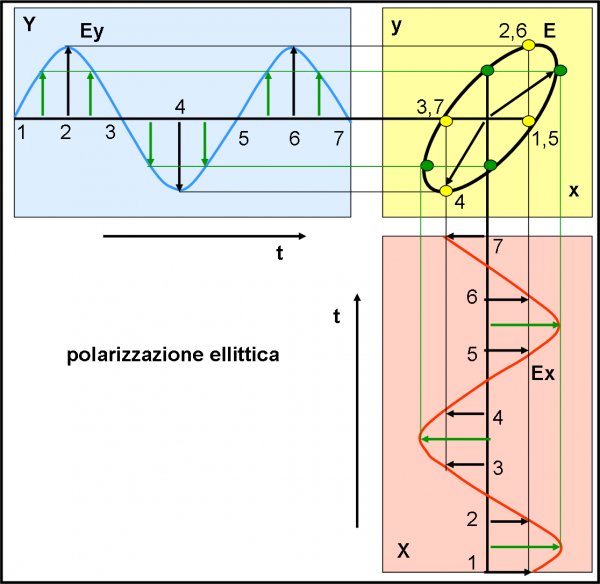
Cosa siamo riusciti a fare con tutte queste figure e con una particolare rappresentazione geometrica? Abbiamo definito i vari tipi di polarizzazione e abbiamo capito, grossolanamente, come poter agire per analizzarla, attraverso strumentazione che filtrino la luce che arriva. A seconda del comportamento si può capire in quale caso siamo. La Natura, spesso e volentieri, è capace di polarizzare la luce attraverso fenomeni fisici particolari, come già detto prima. Ogni fenomeno ha una sua caratteristica e quindi l’analisi della luce polarizzata può indicare che tipo di fenomeno ha agito su di lei.

Risulta anche chiaro un altro concetto. Affinché la luce non sia polarizzata è necessario che le due onde proiettate non abbiano la stessa frequenza. Altrimenti capiteremmo in uno dei casi già trattati. Attenzione, però. Ciò non vuol dire che, in realtà, il campo vettoriale si propaga cambiando la frequenza  della sua oscillazione, ma solo che l’orientazione del piano di oscillazione cambia in modo qualsiasi, senza nessuna regola. Non pensiamo, quindi, di avere sicuramente luce polarizzata se usiamo luce monocromatica. La frequenza è sempre una e una sola, ma la direzione di oscillazione può variare a piacere. Questo cambiamento casuale comporta variazione di frequenza nelle onde proiettate. Studiando queste capiremmo subito che la luce non è polarizzata.

La definizione più esatta di luce non polarizzata è facilmente comprensibile e la ripetiamo ancora: un fascio di luce è normalmente il risultato della sovrapposizione di un gran numero di onde emesse dagli atomi o molecole della sorgente di luce. Ne consegue che il vettore campo elettrico può oscillare in ogni direzione, mantenendosi, però, sempre perpendicolare alla direzione di propagazione dell’onda.

Scusate le ripetizioni, ma ormai mi conoscete bene e sapete che è una delle mie “strategie” divulgative.

Lasciatemi concludere con una constatazione molto importante: la luce, a parte la sua natura, può essere descritta da tre parametri: colore (lunghezza d’onda), direzione di propagazione (sorgente), polarizzazione (regolarità o no dell’oscillazione). Normalmente siamo capaci di filtrare la luce secondo colore e polarizzazione. Più difficile sembrerebbe filtrarla secondo la direzione di provenienza. Recentemente si sono fatti passi avanti anche in questa problematica. Utilizzando strati di sostanze particolari, si è riusciti gradatamente a riflettere, a ogni passaggio, buona parte della luce che non giunge con un certo angolo, attraverso giochi vari di polarizzazione e di angoli di incidenza. Al momento si è in una fase sperimentale, che sta, però, dando ottimi risultati. Le applicazioni sarebbero enormi. In campo astronomico permetterebbero di osservare, tra l’altro, oggetti deboli vicino a sorgenti luminose. Basterebbe lasciar passare solo la luce che proviene dai primi. Lo studio diretto degli esopianeti ne avrebbe un aiuto enorme.

 

Perché l'acqua polarizza la luce? Ne parliamo QUI