NEW: Dieci grammi e vi peserò un mondo!? **
Nella versione precedente non avevo impartito velocità... Meglio cambiare un po' le condizioni. Così dovrebbe essere molto meglio! Abbiate ancora pazienza... Se mi capita di nuovo vuol proprio dire che è meglio che smetta per un po'...
Siete un esploratore spaziale e avete raggiunto un sistema planetario con tre pianeti. Noi sappiamo che il primo ha la massa di Mercurio, il secondo quella della Terra e il terzo quella di Giove. Voi però non lo sapete e dovete cercare di ricavarle. Avete a disposizione solo una pallina di ferro di massa uguale a 10 g (sulla Terra) e nient’altro.
Cosa fate? Vi viene una geniale idea. Costruite una enorme sfera perfetta di ghiaccio, perfettamente liscio, di 1000 kg (avete i mezzi per farlo con l'acqua e gli scarichi raffreddanti dell'astronave) e la trasportate in ciascuno dei pianeti. Poggiate la pallina su di lei e la lasciate libera. Attriti e atmosfera non ce ne sono. Siete convinti che il punto nel quale la pallina lascerà la superficie della sfera (ossia, se ne andrà per la … tangente) vi darà la soluzione. Avete ragione oppure no? Ovviamente dovete dimostrarmelo con qualche semplice formula e trovare (giocoforza) la distanza alla quale se ne andrà per ogni pianeta alieno...
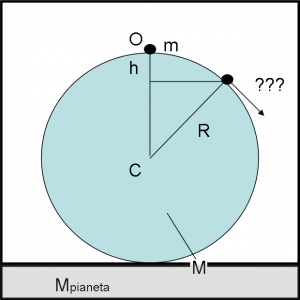
Vi allego una figura esplicativa (ma senza esagerare). La distanza potete misurarla da O verso il basso.
24 commenti
Caro Enzo penso di non avere proprio capito il problema... Perché mai appoggiando un corpo delicatamente al suolo di un pianeta questo dovrebbe volare via da solo? La velocità di rotazione è tale che la forza centrifuga supera la gravità? Altrimenti missioni spaziali gratis per tutti!
Se io dovessi stimare la massa di un pianeta lascerei semplicemente cadere la pallina e ne confronterei l'accelerazione con quella che ha sulla Terra...
Mah, intanto proverei a calcolare il potenziale gravitazionale della Terra alla superficie del pianeta:
Pg = G*M/R = (6,7*10^-11)*(5,98*10^24)/(6,36*10^6) = 6,3*10^7 J/kg
Poi calcolerei l'energia cinetica (per unità di massa) posseduta dalla pallina:
Ec = 0,5*v^2 = 0,5*465^2 = 10,8*10^4 J/kg
La velocità della pallina l'ho posta uguale alla velocità periferica alla superficie della Terra.
Se faccio il rapporto tra i due valori, ottengo: Pg/Ec = 582
La pallina sicuramente non partirà per la tangente e questo effetto lo vedrò, pur non conoscendo la massa del pianeta.
D'altra parte, poggiando delicatamente a terra la pallina, le imprimerò automaticamente la mia velocità (riflesso della rotazione del pianeta) per cui la pallina dovrebbe rimanere nel punto della deposizione.
Il caso di Giove non lo considero, supponendo (ma non ho fatto i calcoli) che la grande massa sopravanzi abbondantemente l'effetto della velocità.
Vediamo cosa succede su Mercurio:
Pg = G*M/R = (6,7*10^-11)*(3,3*10^23)/(2,4*10^6) = 9,2*10^6 J/kg
Ec = 0,5*v^2 = 0,5*3^2 = 4,5 J/kg
La condizione di (quasi) sincronismo rotazione/rivoluzione dovuta alle forze mareali del Sole lo ha rallentato a tal punto che Pg è molto, molto, ma molto maggiore di Ec.
Insomma, a me pare che non accada nulla su nessuno dei tre pianeti.
N.B.: Non si potrebbe fare un'interurbana a Cavendish?
Ma dai Enzo, su Mercurio la palla di ghiaccio si scioglierebbe rapidamente ....
Pensavo di aver sbagliato di nuovo... ma no, non ho detto che sono alla distanza dei nostri, solo che hanno massa uguale
Non so perchè ma mi viene in mente la caduta di un grave dalla coffa di una nave in navigazione. Gli antichi speravano di ricavare, osservando il punto di caduta del grave sulla tolda ....
bando alle ciance Alvy e giù con le formule!
Questa volta sono sicuro (??!!) di non aver fatto errori!
Scusa Enzone, ma non manca un dato?
Qualche post fa ti ho scritto che avrei voluto chiedere aiuto Cavendish , ora mi servirebbe Eratostene.
Sbaglio?
A me invece ora sembra ben definito, prima avevo capito che la pallina volasse via dal pianeta!
La velocità iniziale immagino sia da considerare infinitesima, giusto per rompere l'equilibrio instabile.
Va bene, io mi ci provo.
Il peso specifico del ghiaccio, sulla Terra, è pari a 0,9 kgp/dm^3.
Una sfera di ghiaccio del peso (terrestre) di 1.000 kg avrà dunque un volume di 1.111 dm^3 ed un conseguente raggio di 6,4 m.
La pallina posta sulla sommità della sfera di ghiaccio è inizialmente ferma; trovandosi però in una posizione di equilibrio instabile comincerà a muoversi lungo un cerchio massimo della sfera. Non considero qui eventuali accelerazioni di Coriolis dovuti al fatto che la sfera è a sua volta trascinata dal moto del pianeta sottostante.
Provo ad introdurre un bilancio energetico ipotizzando che l’accelerazione di gravità a cui è sottoposta la pallina sia costante, visto che si sposta restando sempre in prossimità della superficie del pianeta, la sua altezza massima essendo pari a 12,8 m (6,4x2):
mp*g*2*r = 0,5*mp*v^2
in cui
mp massa della pallina;
g accelerazione di gravità alla superficie del pianeta;
r raggio della sfera di ghiaccio;
V velocità della pallina al suolo.
Misurando la velocità con cui la pallina raggiunge il suolo posso calcolare il valore di g.
V^2 = 4*g*r
Essendo, sulla Terra, g = 10 m/s^2 ottengo v = 16 m/s.
Ora, per ricavare la massa del pianeta posso impostare la seguente uguaglianza:
mp*g = G*M*mp/R^2
in cui
M massa del pianeta;
R raggio del pianeta.
Risolvendo, ottengo:
M = g*R^2 / G
Posso calcolare M a patto di conoscere R.
O no?
Riguardo al puto di caduta della pallina sulla superficie del pianeta, mi sembra che debba cadere sulla verticale, ovvero a 6,4 m dal centro della sfera di ghiaccio. La pallina infatti condivide la stessa velocità della sfera, da cui l'esempio del veliero che ho riportato qualche post fa.
no, questa volta non mancano dati... ci sono tutti... Sì R te lo potrei anche dare, ma... non è importante. Vogliamo la massa, non il raggio del pianeta. Sempre che ci si riesca, ovviamente... Alvy, il problema non è ben posto... E, oltretutto, poco importa la massa della sfera di ghiaccio, che rimane sempre irrisoria rispetto a quella del pianeta. Ah... potete anche non fare girare i pianeti...
Alvy ad occhio mi sembra che una sfera di ghiaccio con r=6,4 metri pesi più di 1000kg
Ciao SMA, tutto ok?
Hai ragione, porca miseria. Non ho fatto la conversione da decimetri a metri.
Il raggio è di 6,4 dm, cioè 0,64 m.
Mi sto rinc.... , bah, sarà l'età.
Però Enzone ci ha dato una bella gatta da pelare. Che ne dici?
Caro SMA, ti scrivo sottovoce così Enzone non mi sente!
Il fatto è che non basta riuscire a calcolare l'accelerazione di gravità alla superficie del pianeta perchè detta accelerazione è funzione della massa M ma anche del raggio R, secondo l'espressione g = G*M/R^2
Esistono quindi infinite soluzioni possibili; basta variare la massa in ragione del quadrato del raggio per ottenere lo stesso valore dell'accelerazione g.
Bisogna dunque cercare un altro parametro legato alla caduta della pallina dalla sfera di ghiaccio. Secondo me la pallina cade sempre nello stesso punto, quale che sia la massa del pianeta e quindi non si riesce a determinare un beneamato ... ciufolo, a parte la velocità di caduta al suolo che varia di sicuro.
Comunque voglio pensarci ancora un pò. Buona serata.
Anch'io Alvy sono arrivato a trovare g misurando la velocità con cui la pallina impatta la superficie, purtroppo però mi trovo sempre di mezzo il raggio del pianeta... mah!
cari amici,
scriviamo un po' di formulette e vedrete che le cose si chiariranno... Ah, la meccanica classica!!! E leggete bene lo scopo dei calcoli (nell'articolo è scritto chiaramente...)
aggiunta: sapete bene che io (quando non sbaglio
) cerco di condire una fettina di carne ai ferri con mille cosucce che cercano di farla passare per chissà cosa... ma in fondo è sempre una fettina ai ferri! 
Fermo restando che non sono affatto contento di me stesso, visto che ho impiegato un tempo biblico a trovare la strada giusta
, ti chiedo se la fettina l'ho cotta a puntino oppure l'ho .... bruciata!
Il magico angolo di 42° mi ha fatto venire in mente un'altra questione sicuramente collegata al nostro problema.
Se provate a lasciar cadere dal pugno chiuso un sottile flusso di sabbia (ovviamente asciutta e tenendo sempre ben ferma la mano) otterrete un cono il cui angolo d'inclinazione sull'orizzontale ha un valore fisso.
Se non ricordo male tale angolo (valore massimo possibile) vale appunto 42°.
Attendo ... fiducioso
mmm... attendo qualcosa di più preciso... si può fare, forza!
Non mi fai sconti eh?
Beh, giusto così!
Allora, la formula si può rendere più ... elegante nel modo che segue visto che, in effetti,
sinθ = (h-R)/R.
h <(5/3)*R condizione per cui la pallina parte per la tangente, dove:
h è la quota della pallina rispetto alla base su cui poggia la sfera,
R è il raggio della sfera di ghiaccio.
Adesso però la spiegazione la fornisci tu!
caro Alvy...
bene hai trovato il punto di caduta (BRAVO). Non si può fare nient'altro per ottenere lo scopo finale? Di cosa avresti bisogno...?
va bene, va bene, basta così... non vorrei confondere le idee ad altri che non siano Alvy
In realtà, il succo era trovare la distanza del punto di caduta della pallina. Per trovare la massa non basta ricavare g (sempre possibile), ma bisogna avere il raggio e/o la densità del pianeta (come detto dai nostri amici).
Comunque, il fatto che la pallina cade a un'altezza che dipende solo dal raggio della sfera e non dal pianeta è già un bel risultato non del tutto intuitivo.
Domani mattina metto "in bella" il procedimento che è praticamente quello di Alvy...
Mah, Enzo, mi pare si torni a quanto ho già scritto.
Se la pallina è inizialmente ferma sulla sommità della sfera avrà energia cinetica iniziale pari a 0.
Quando tocca il pianeta la pallina avrà energia cinetica finale Ec pari a 0,5*mp*v^2.
D'altra parte l'energia potenziale della pallina sarà variata di mp*g*2*Rs, in cui:
g è l'accelerazione di gravità che considero costante lungo il percorso della pallina,
Rs è il raggio della sfera.
Dunque: 0,5*mp*v^2 = mp*g*2*Rs. Di qui ricavo g:
g = 0,5*v^2/(2*Rs) = v^2/(4*Rs).
Posso inoltre scrivere che: F = mp*g = (G*mp*M)/Rt^2, in cui:
Rt è il raggio del pianeta.
v^2/(4*Rs) = (G*M)/Rt^2.
Se conosco Rs e v (misurabile), posso trovare M avendo Rt.
mmh ... ho l'impressione che non ti soddisferà. Non è molto elegante e forse c'è qualche scorciatoia che non vedo (ancora...)
Ooooops non avevo letto il tuo ultimo post!
caro Alvy,
sfera o non sfera, se si conosce il raggio basta far cadere la pallina al suolo senza sfera e si ha subito la relazione tra g e il tempo di caduta e quindi la massa. La sfera non serve a niente! D'altra parte le masse delle stelle o dei pianeti si determinano attraverso qualcosa che gli passi vicino (una compagna o una navicella di massa nota). Nel nostro caso, doveva vedere come variava il suo moto passando vicino ai vari pianeti. Con la sfera di ghiaccio poteva farsi tanti bei gelati!
Scrivo un attimo la risposta per i lettori... Comunque, sono "costretto" a dirti bravo, accidenti!!!