Come avete già capito dai vari commenti, la pallina e la sfera di ghiaccio non servono a niente per calcolare la massa di un pianeta. Bisogna usare le leggi di Keplero e avere a disposizione due masse, di cui una conosciuta (per esempio la navicella stessa). Non per niente la massa è uno dei parametri meno conosciuti delle stelle e si risolve in qualche modo solo per i sistemi binari.

Per calcolare invece l’accelerazione gravitazionale (g) di ogni pianeta, basta far cadere la pallina al suolo (qualsiasi sia la sua massa) e misurare il tempo di caduta. La sfera di ghiaccio non aggiunge nessuna informazione! Senza il raggio (o la densità) del pianeta si rimane, però, senza massa.

Tutta la sceneggiata l’avevo costruita per prendere un po’ in giro Alvy (che non è uno sprovveduto, però…), ma il vero scopo del Quiz era di calcolare il punto di caduta di una pallina lasciata libera su una sfera di raggio R sotto l’effetto della sola gravità del pianeta. Un giochino “classico” che non è del tutto intuitivo.

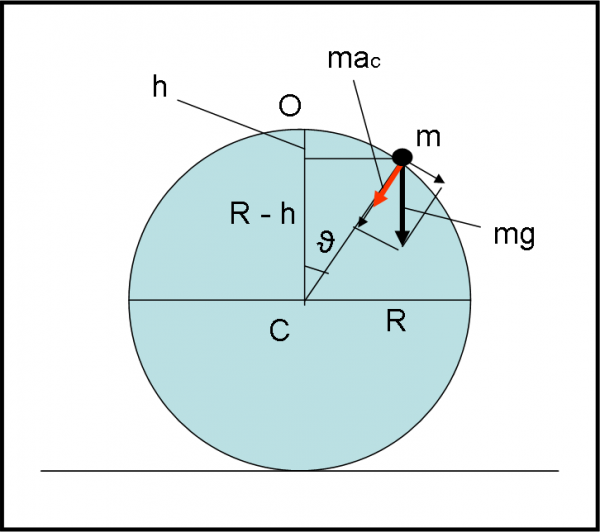
La Figura illustra ogni passaggio necessario al problema.

Analizziamolo, cominciando a definire le forze a cui è soggetta la pallina di massa m. Essa subisce la gravità del pianeta e questa forza è diretta verso il basso. L’accelerazione continuiamo a chiamarla g come sulla Terra.

F_g = m g

Inoltre, la pallina si nuove di moto circolare attorno al centro C della sfera di ghiaccio e subisce una forza centripeta che vale:

F_c = m a_c

La prima forza è diretta verso il basso, mentre la seconda è diretta verso il centro della sfera di ghiaccio.

La forza di gravità può essere scomposta in due componenti: una tangente alla sfera e una diretta verso il centro. Basta un po’ di trigonometria banale per trovare che la componente radiale, F_gR, diretta verso il centro, è data da:

F_gR= m g cosϑ

Cosa tiene la pallina a contatto della sfera è la risultante delle forze che agiscono in senso radiale. La componente tangenziale (dovuta solo alla gravità) è proprio quella che vuole farla scappare per la tangente.

In altre parole, chi comanda è la differenza:

mg cosϑ – ma_c

La pallina se ne va per la tangente quando:

mg cosϑ – ma_c = 0

Ossia:

g cosϑ = a_c

E, ancora:

cosϑ = a_c/g    …. (1)

La massa m della pallina è già scomparsa e ciò vuol dire che poteva essere qualsiasi. Comunque resta ancora g che è legata strettamente alla massa del pianeta.

Non ci resta che utilizzare la solita conservazione dell’energia del sistema. L’energia totale è data dalla somma dell'energia potenziale e dell'energia cinetica. Siamo, in fondo, nel caso delle famose montagne russe (gira e rigira le relazioni sono sempre le stesse):

E = E_cin + E_pot

Prima che la pallina si muova l’energia è solo potenziale:

E = 0 + E_pot = mgh

Quando la pallina se ne va per la tangente, l’energia è solo cinetica:

E = E_cin + 0 = ½mv²

Ma l’energia si deve conservare perciò:

½mv² = mgh

Ossia

v² = 2gh  …. (2)

Sappiamo però dalla cinematica del moto circolare che:

a_c = v²/R    (l’abbiamo già ricavata varie volte)

Andiamo a sostituire questo valore nell’espressione del coseno (1)

cosϑ = a_c/g = v²/Rg

La (2) ci regala il valore di v² e, sostituendo, si ha:

cosϑ = 2gh/Rg = 2h/R    …. (3)

Accidenti, è sparita anche l’accelerazione di gravità e, quindi, la massa del pianeta…

Proseguiamo…

Un po’ di geometria ci dice immediatamente che:

cosϑ = (R–h)/R

La (3) diventa:

(R–h)/R = 2h/R

E, infine:

h = R/3

Abbiamo trovato che la pallina lascia la sfera sempre nello stesso punto, indipendentemente dalla massa della pallina e dalla massa del pianeta. Tutto dipende solo dal raggio della sfera di ghiaccio. Insomma, l’idea non era affatto geniale! In ogni modo abbiamo ricavato il punto in cui una pallina che scivola su una sfera l’abbandona per andarsene per la tangente. E non è cosa da poco! Potete sempre provare a casa…