Categorie: Fisica classica
Tags: differenza vettori prodotto scalare quiz somma vettori versori vettori
Scritto da: Vincenzo Zappalà
Commenti:2
SOLUZIONE del quiz sulla guerra pacifica di Papalla **
Possiamo quindi ragionare anche senza figure (che alla fine, però, inseriamo comunque… )
Due vettori sono perpendicolari tra loro quando il loro prodotto scalare è uguale a zero. Scriviamo perciò i due vettori a un certo tempo t ed eseguiamone il prodotto scalare utilizzando la scomposizione nei due versori i e j.
Il primo si scrive:
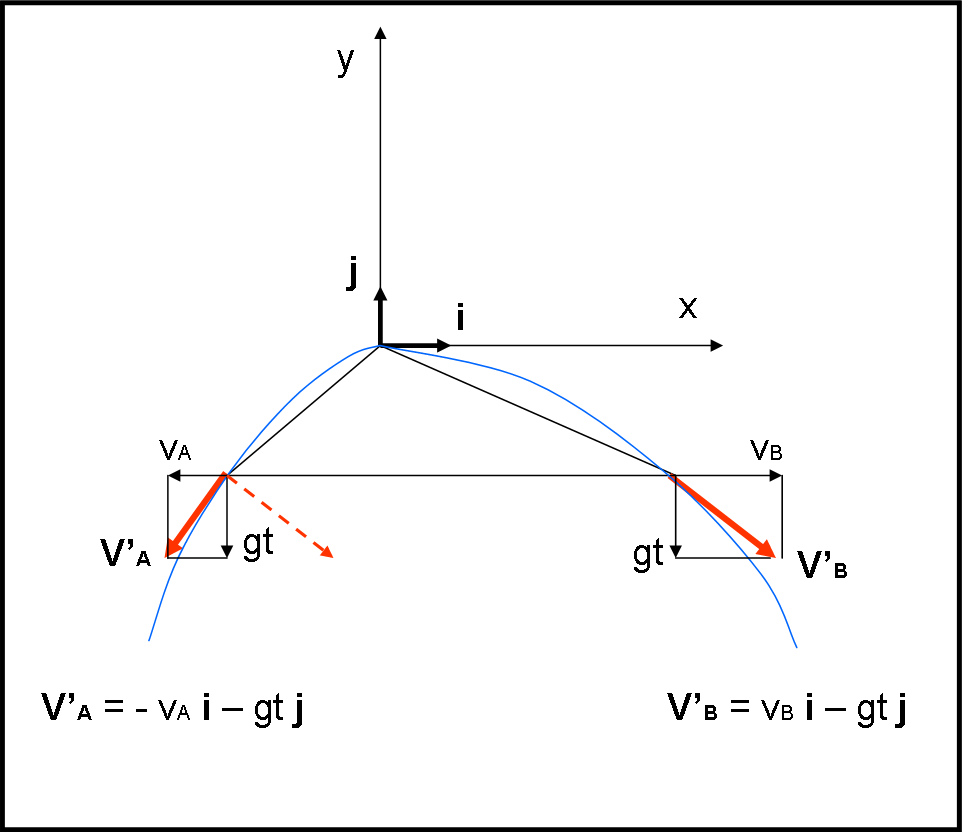
V’A = - vA i – gt j
Il secondo si scrive:
V’B = vB i – gt j
Gli assi cartesiani sono stati scelti verso destra e verso l’alto. Le due componenti rappresentano un moto rettilineo uniforme lungo l’asse x e un moto uniformemente accelerato lungo l’asse y (gravità).
Basta allora eseguire il loro prodotto scalare e porlo uguale a 0. Non solo, però. Sappiamo già che il prodotto scalare di due vettori è dato dalla somma dei prodotti delle rispettive componenti (scalari) sugli assi cartesiani e che i x j = 0, mentre i x i = 1.
Abbiamo perciò, immediatamente, che :
V’A x V’B = 0 = -vA vB + g2t2
Da cui:
t = (vAvB)1/2/ g
Praticamente, un solo passaggio
Al tempo t le posizioni delle due palline possono essere rappresentati dai due vettori rA e rA che si possono scrivere (ricordando le equazioni del moto rettilineo uniforme e di quello uniformemente accelerato):
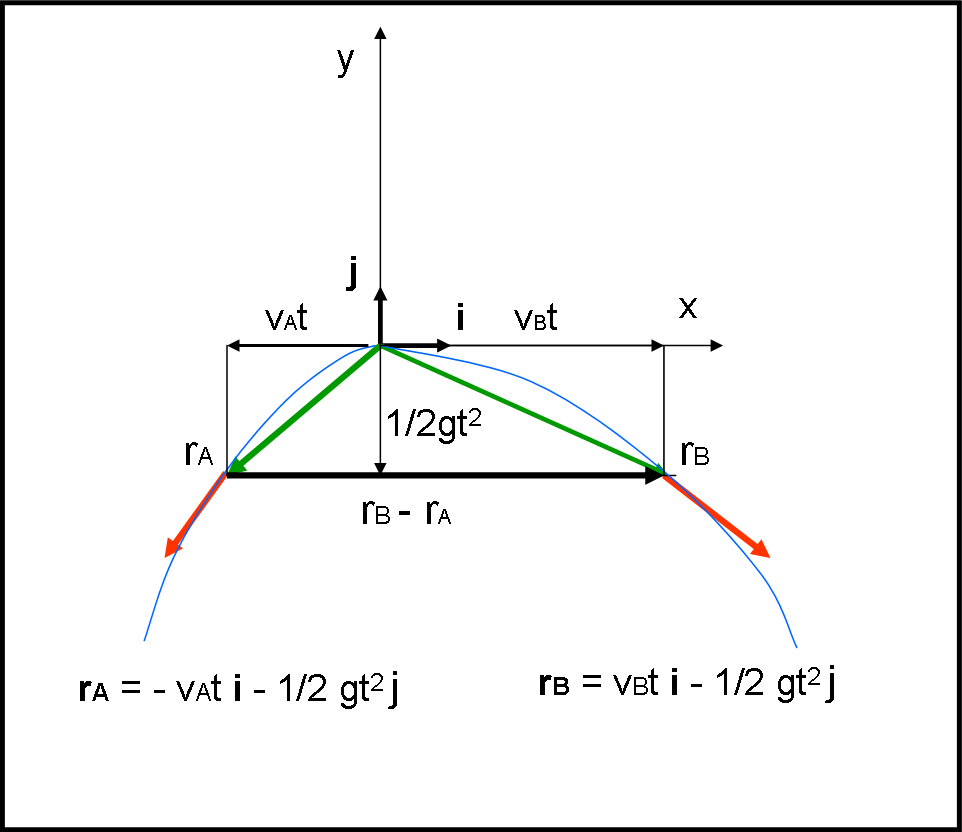
rA = - vAt i - 1/2 gt2 j
e
rB = vBt i - 1/2 gt2 j
A noi interessa il modulo del vettore differenza, ossia |rB – rA|
Sappiamo benissimo, però, che le componenti del vettore somma sono la somma delle componenti dei due vettori di partenza. Per cui:
|rB – rA| = (vB + vA)t - 1/2 gt2 + 1/2 gt2 = (vB + vA)t = (vB + vA) (vAvB)1/2/ g
Ossia:
|rB – rA| = (vB + vA) (vAvB)1/2/ g
Un altro solo passaggio…
Non c’è altro da dire, a parte riportare le due figure esplicative.
Come capita sempre, vi sono diversi modi per giungere alla soluzione. Io ho voluto usarne uno che facesse uso solo e soltanto delle operazioni vettoriali (somma e prodotto scalare) e della scomposizione lungo i versori. In questo caso il vantaggio rispetto ad altri metodi può sembrare insignificante, ma crescerebbe di molto se la faccenda si complicasse e si andasse nelle tre dimensioni.
Invito tutti ad andare a (ri)leggere le operazioni con i vettori (nella fisica -e non solo in quella classica- sono importantissimi!). Se poi, rimanessero ancora dubbi, ditemelo e spiegherò più dettagliatamente la soluzione.
La prossima volta ci facciamo una bella nuotata!






2 commenti
Per prima cosa un saluto a tutti i partecipanti del blog, e soprattutto a te Vincenzo.
E’ la prima volta che scrivo, ma è un pochino che seguo i tuoi articoli (qualche mese) e devo dire che sono abbastanza chiari, anche se alcuni dubbi mi rimangono (non per colpa tua ma unicamente mia).
Sono sempre stato indeciso di partecipare per paura di dire delle fesserie, purtroppo mi mancano molte basi sia matematiche che fisiche.
Ho fatto solo le superiori (istituto tecnico) e molte cose di base come la cinematica o la termodinamica sono state trattate a scuola, ma ora mi rendo conto che sono state affrontate in modo un po’ troppo superficiale e incompleto.
Io ho un grosso difetto: quello di voler capire l’essenza del concetto trattato e di assimilarlo o convertirlo secondo la mia logica.
Io penso che solo così si possa capire qualcosa.
Imparare a memoria delle formule o dei concetti per quanto possono essere chiari all’inizio non serve a niente, al primo problema serio uno si perde nel nulla, perché non è in grado di applicare ciò che ha imparato.
Fatta questa premessa, veniamo a noi.
Da questo quiz ho capito che non ho capito niente… non tanto per la soluzione che è chiara, anzi fino al calcolo del tempo ci ero arrivato anche io sia usando i vettori (dopo aver letto un tuo articolo precedente) che la trigonometria, ma per l’uso e il significato dei vettori stessi.
In pratica se ho capito bene si può usare un vettore per trattare svariate cose.
Io ero rimasto tipo al vettore forza che di per sé vuol dire tutto o niente, nel senso che a livello pratico non è altro che uno strumento per rappresentare una forza applicata in un punto inteso come un valore di intensità, una direzione e un verso di applicazione.
Poi posso sommare o sottrare le varie forze vettore per trovare la risultante (il modulo, la direzione e il verso) o scomporre per trovare la forza lungo una direzione particolare, se mi serve per fare un certo calcolo.
A scuola usavamo il metodo del parallelogramma nel vero senso della parola con carta millimetrata e righello, poi disegnavamo il tutto e misuravamo, al massimo facevamo qualche calcolo sui triangoli nei casi semplici, quando gli angoli lo permettevano.
Invece se ho capito bene posso usare il vettore anche per rappresentare un punto nello spazio, ovvero un punto in un sistema di assi cartesiani x y non è altro che un vettore che va dall’intersezione degli assi stessi (i miei zeri nello spazio) al punto stesso.
Infatti se lo disegniamo, esso è caratterizzato da un modulo (distanza del corpo dallo zero di riferimento), una direzione (quella di spostamento del corpo) e un verso: è un vettore a tutti gli effetti.
A livello pratico cosa implica? ... semplice, possiamo rappresentare il moto di un corpo nello spazio a più dimensioni (non solo x y ma anche x y z o anche oltre) semplicemente usando un unico termine matematico e possiamo calcolare quello che vogliamo (o quasi) solo con formule matematiche senza dover fare grafici e usare angoli o quant’altro, che a un certo punto potrebbe diventare molto difficile e incasinato.
Riassumendo, io ho sempre trattato i moti lungo una sola direzione e applicato le relative funzioni, ma se invece il corpo si sposta in x e y come in questo caso, come facciamo?
Io finora ho calcolato le funzioni di spazio nelle due direzioni privilegiate (gli assi cartesiani) ognuna con la sua velocità, poi sommavo l’effetto risultante e trovavo geometricamente la risultante.
Ma questo implica dover sempre ragionare e “tirarsi dietro” più formule per trovare un certo punto in x y.
Infatti mi sono sempre chiesto se esistesse un mezzo matematico semplice e in un unico termine per rappresentare un punto in due dimensioni (o anche di più).
La risposta è il vettore.
Se questo è vero, possiamo usare i calcoli con i vettori per studiare il moto di un corpo.
Possiamo scomporre il vettore posizione nei due versori orizzontale e verticale che guarda caso il modulo è rappresentato dalle funzioni del moto del corpo lungo l’asse.
Possiamo trovare delle condizioni particolari come l’angolo tra i vettori velocità di due corpi che si muovono nello spazio x y, senza scomodare la trigonometria.
Possiamo calcolare la distanza di due corpi facendo la differenza dei due vettori posizione, in particolare la distanza inteso come valore scalare è il modulo del vettore differenza.
Concludendo devo dire che rappresentare un punto con un vettore mi ha aperto un nuovo mondo… no dai sto scherzando.

Però è un vettore di vista, pardon punto di vista particolare che non conoscevo e che a scuola non mi hanno insegnato.
Spero di non essermi dilungato troppo, e che quello che ho scritto (sperando che sia corretto) possa aver aiutato altre persone con i miei stessi dubbi.
Ovviamente se l’argomento è già stato trattato a suo tempo, chiedo scusa per la ripetizione, ma immagino che, come me, non tutti hanno letto il blog dall’ inizio.
Se ho detto delle fesserie chiedo umilmente scusa, ma così facendo almeno mi rendo conto dei miei errori.
In futuro cercherò di partecipare di più anche se il tempo a disposizione è poco e io sono anche lento a elaborare e capire le informazioni.
Un saluto a tutti
Simone
caro Simone,
hai detto molte cose giuste. I vettori possono essere utilissimi nel descrivere un certo fenomeno e renderlo risolvibile. Un esempio classico sono le leggi di Keplero che possono essere trovate partendo dalla legge di Newton e lavorando sui vettori accelerazione e velocità. Come dici bene tu, i vettori sono applicabili ovunque, quando esiste un modulo, una direzione e un verso. Sono vettori la quantità di moto, il momento angolare, la velocità, l'accelerazione, la posizione di un punto, ecc., ecc. Spesso si semplifica tutto lavorando su un solo asse ed allora il modulo basta e avanza. In generale, però, solo i vettori possono rappresentare sinteticamente una grandezza in n dimensioni... Se hai tempo a leggere la QED, vedrai come la meccanica quantistica abbia fato grande uso di loro e delle loro proprietà...
Che dirti... non aver paura a esprimerti e a dire "fesserie". Non esistono fesserie quando si cerca di capire e di usare il cervello. Come si diceva una volta: nessuno nasce imparato e tutti abbiamo da imparare qualcosa, sempre e ovunque!
Dai, continua a seguirci e un po' alla volta vedrai che abbiamo trattato di tutto e di più,dalla meccanica più semplice alla MQ più complessa. La vera Scienza ha un grande merito: la semplicità!!!