Approfittiamo della soluzione al quiz sul "naufrago" per fare un piccolo ripasso di derivate e di studio di funzione. Un caso veramente elementare... credetemi!

Questo esercizio è veramente semplice dal punto di vista fisico e si risolve facilmente ricordando lo studio di funzioni. La prima cosa che dobbiamo fare è, quindi, costruirci una funzione da studiare per trovare i suoi punti particolari.

Ciò che c’interessa sapere è il tempo impiegato dal naufrago per raggiungere il punto di ristoro. La nostra y è, perciò, il tempo impiegato, ossia t. Il tempo ovviamente varia a seconda del percorso e dobbiamo cercare un’incognita x che serva a descrivere il tragitto. Possiamo usare la distanza a partire dal punto B, che cresce verso C. In altre parole, la nostra x è misurata con l’origine in B ed è positiva verso C.

Il tempo t è legato alla x dalla relazione che definisce la velocità (proprio i termini noti):

t = x/v      (velocità costante per definizione)

Nel percorso in mare è:

t = x/2

Nel percorso sulla sabbia è:

t = x/1 = x

Non ci resta che esprimere un percorso qualsiasi che congiunga A con C e scrivere il suo tempo di percorrenza in funzione della x così definita. Questa sarà la nostra funzione f(x).

Il tragitto può sempre essere spezzato in due parti: la prima in mare e la seconda sulla sabbia. Consideriamo D come punto qualsiasi (Fig. 1).

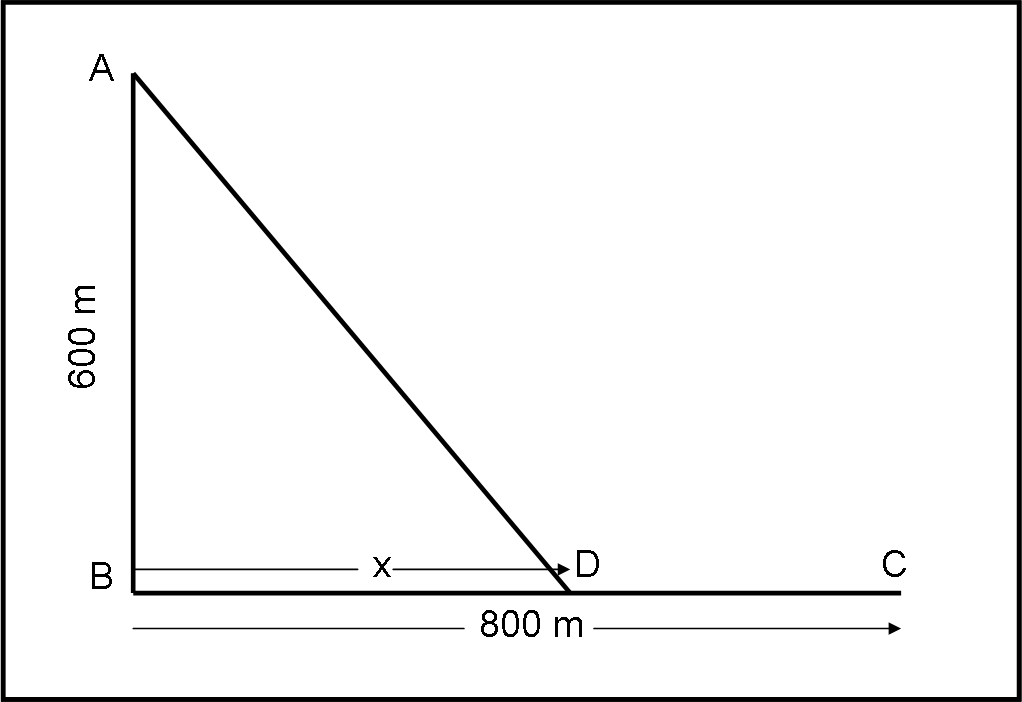
Abbiamo che il percorso p da compiere è dato da:

p = AD + DC

A noi interessa il tempo t necessario a compiere p. Per ottenerlo, basta dividere AD (che si compie in mare) per la velocità v = 1 m/s e DC (che si compie sulla sabbia) per la velocità v = 2 m/s. Ossia:

t = AD/1 + DC/2

Scriviamo, allora, AD e DC in funzione dell’ascissa x del punto D. Si ha:

AD = (AB² + BD²)^1/2 = (600² + x²)^1/2

DC = (BC – BD)/2 = (800 – x)/2

Sostituendo, otteniamo:

t = (600² + x²)^1/2 + (800 – x)/2     …. (1)

Questa è proprio la funzione t = f(x) cercata, che bisogna studiare per trovare il suo valore MINIMO (ossia proprio il tempo minimo di percorrenza richiesto).

Essa non va da meno infinito a più infinito, ma è decisamente limitata tra x = 0 (il naufrago giunge sulla spiaggia  lungo AB e poi corre su di essa fino a C) e x = x_C = 800 (il naufrago decide di nuotare direttamente fino C “in diagonale”, compiendo il percorso sicuramente più corto, ma a velocità ridotta).

Calcoliamo, innanzitutto, il tempo impiegato dal naufrago seguendo questi due percorsi limite. Essi ci danno i limiti estremi della funzione t = f(x), dato che x può solo variare tra 0 e 800.

t_x=0 = (600² + 0)^1/2 + (800 – 0)/2 = 600 + 400 = 1000 sec

Se il naufrago nuotasse fino a B e poi corresse da B a C impiegherebbe un tempo di 1000 sec.

Calcoliamo, adesso, il tempo per il percorso completamente svolto in mare:

t_x=800 = (600² + 800²)^1/2 + (800 – 800)/2 = (360 000 + 640 000)^1/2 = 1000 sec

Se il naufrago nuotasse direttamente da A fino a C impiegherebbe nuovamente il tempo di 1000 sec.

La nostra funzione t = f(x) inizia e finisce con un valore di 1000 sec. In parole più tecniche, nel sistema di coordinate cartesiane (x,t), la funzione inizia dal punto P(0, 1000) e termina nel punto Q(800,1000). Disegniamo la Fig. 2 che descrive questa situazione.

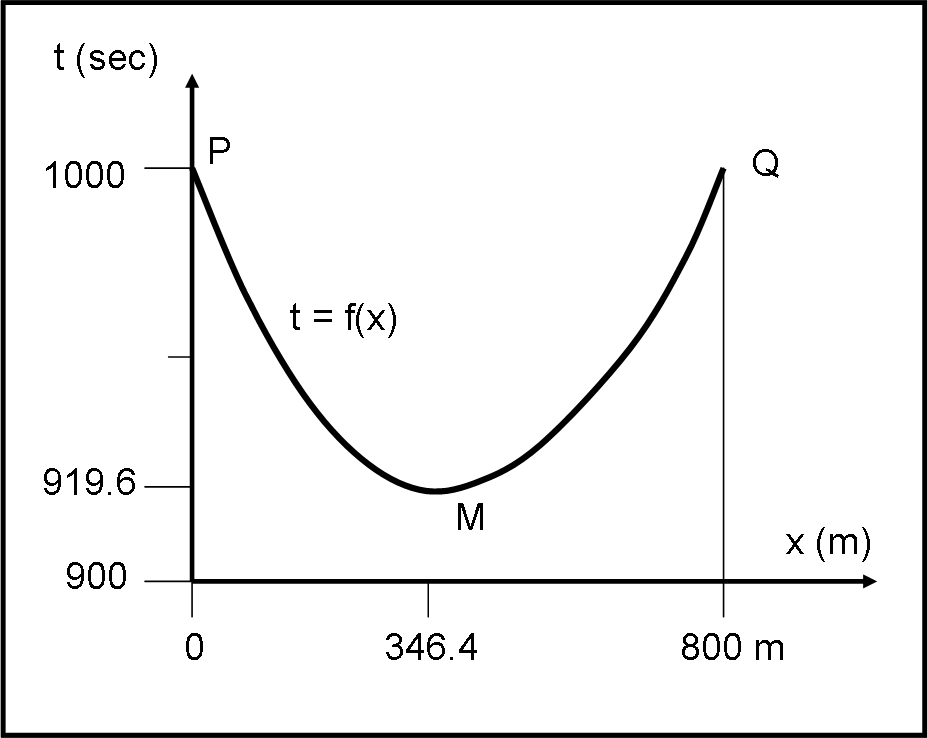
Siamo caduti in un classico esempio di studio di funzione e possiamo trovare altri punti particolari. Beh… dopo i due estremi non ci sarà molto da fare, se non trovare gli eventuali massimi e/o minimi (e magari anche i flessi).

Non ci resta che eseguire la derivata prima della funzione e trovare la x che l’annulla. Poi vedremo se è un massimo o un minimo o che altro…

t = (600² + x²)^1/2 + (800 – x)/2

t’ = x/(x² + 600²)^1/2 - 1/2    …. (2)

Non ho svolto tutti i passaggi, ma questo dovete provare a farlo voi, ricordando quanto abbiamo spiegato nella serie di articoli sulla “matematica”. Bisogna ripassare le derivate delle potenze, delle costanti, della somma e cose del genere…

Poniamola uguale a zero e cerchiamo il (i) valore (i) di x che l’annulla:

x/(x² + 600²)^1/2  - 1/2 = 0

x/(x² + 600²)^1/2  = 1/2

2x = (x² + 600²)^1/2

Eleviamo a quadrato entrambi i membri dell’uguaglianza

4x² = x² + 600²

3x² = 600²

x² = 600²/3

In realtà, sembra che esistano due soluzioni che annullino la derivata, ossia:

x = +/- 600/3^1/2 = +/- 600/1.7321 = +/- 346.4 m

Tuttavia, possiamo escludere subito la soluzione con il segno meno, dato che sappiamo che la x può andare solo da 0 a 800 m ed è quindi SEMPRE positiva.

La soluzione accettabile è quindi una sola:

x = BD = 346.4 m

Questo valore rende massima o minima la funzioni f(x)? Basta sostituirlo nella (1) e vedere cosa diventa t. Proviamo subito:

t = (600² + x²)^1/2 + (800 – x)/2

t = (600² + 346.4²)^1/2 + (800 – 346.4)/2 = 919.6

Il risultato può venire leggermente diverso a seconda del numero di decimali che avete preso per la x che annulla la derivata prima… Tuttavia, resta il fatto che t_346.4 è nettamente inferiore ai due valori estremi uguali a 1000 sec. Ne consegue, intuitivamente, che il tempo minimo di percorrenza è t_min = 919.6 sec, che si ottiene nuotando il tratto da A a D (di ascissa 346.4 m) e poi correndo sulla sabbia fino a C (la cui x è uguale a 800 m).

Tuttavia, potremmo anche fare i raffinati e calcolare la derivata seconda e vedere che segno assume per x = 346.4.

Per chi vuole provare… il risultato è:

t” = 600²/(x² + 600²)^3/2

Non vi è nemmeno bisogno di fare tanti calcoli. Sostituendo a x un numero positivo la t” assume  valori sempre positivi, per cui il punto considerato DEVE essere un punto di minimo. Ovviamente, non possono esistere punti di flesso obliqui dato che la derivata seconda è sempre positiva.

La funzione può essere facilmente disegnata nella Fig. 2: si ha una curva che assomiglia a una parabola “deformata”. Essa ci dice al variare di x qual è il tempo impiegato dal naufrago. Chi vuole, può anche calcolare la tangente alla curva nei punti estremi…

Possiamo facilmente ricavare il percorso in metri effettuato dal naufrago per raggiungere il punto di ristoro. Egli ha percorso s_m = (600² + 346.4²)^1/2 = 692.8 m, in mare, e poi s_s = 800 – 346.4 = 453.6 m, correndo sulla spiaggia.

Comunque… buon ripasso delle derivate e dello studio di funzione!