QUIZ: la tredicesima fatica di Ercole **
Il re di Tebe aveva già approfittato delle “qualità” fisiche di Ercole, vero e proprio “incredibile Hulk” dell’antichità, e non ha avuto problemi a chiedergli una nuova fatica, diretta solo alla sua sfrenata ambizione.
Il monarca si è fatto costruire una specie di piramide, simile a un vero e proprio monte. Sulla cima vuole, però, porre un’enorme sfera di pietra, finemente lavorata dai suoi schiavi. La sfera è pesantissima e nessuna tecnica di trasporto è riuscita a portarla fino alla sua sede finale. Dopo avere frustato a lungo gli schiavi e gli architetti, non gli rimane che rivolgersi a Ercole.
Il nostro eroe, molto lentamente, riesce a spingere la sfera fino al basamento superiore (Fig. 1), ma ora la situazione si complica non poco.

Mentre la salita fino a quel punto è stata aiutata dall’angolo di inclinazione della piramide, relativamente modesto, adesso si trova di fronte a un gradino da dover superare con la sola forza delle sue braccia. La situazione la vediamo nella Fig. 2
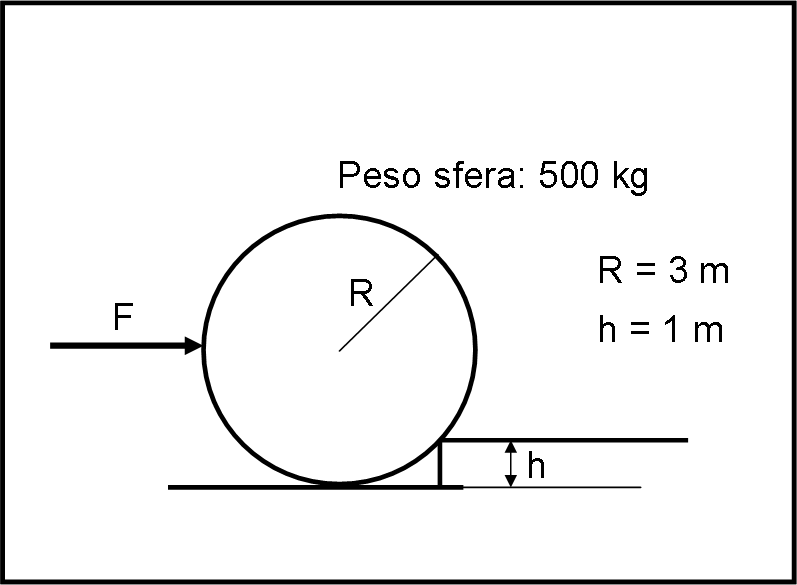
Il peso della sfera P è uguale a 500 kg, mentre il suo raggio R è di 3m. Lo scalino da superare ha un’altezza h di 1 m.
Domanda: “Che forza F deve esercitare Ercole per riuscire a portare la sfera sopra il basamento finale?” Ovviamente, come sempre, nessun attrito…
Anche se solo col pensiero, cerchiamo di dare una mano al grande Ercole!






25 commenti
Allo spunto 559 Kg, poi sempre meno e dopo 2,24 metri di avanzamento F diventa zero.
Sperando di averlo impostato bene:
d=distanza verticale tra punta del gradino e centro sfera=0.5 m
alpha=angolo tra asse orizzontale passante centro sfera e retta congiungente centro sfera e punta del gradino= arcosen (0.5/1.5)=19.47°
k=distanza orizzontale tra centro sfera e punta del gradino=1,5*cos(alpha)=1.41
dall'equilibrio dei momenti (calcolati rispetto la punta del gradino):
Fd+MgK=0
da cui:
F>Mgk/d
F>13832.1 N
caro Luigis,
qualche formuletta per capire come sei arrivato alla soluzione...
caro Davide,
prima di iniziare... perché dici che la distanza verticale tra centro della sfera e spigolo del gradino è 0.5 m? 3 - 1 = 2... O ho capito male?
Oops.... no.... ho ragionato su una sfera di diametro 3m e non raggio.... !!!
Quindi raggio 1.5m e dunque 1.5-1=0.5
tutto sbagliato dunque, almeno a livello di numeri....
rifacendo al volo i calcoli con la sfera di raggio 3m:
d=2m
alpha=41.81°
k=2.23m
F>5483.95 N
attendo altre risposte... ovviamente...
Mah, direi che la condizione dovrebbe prevedere l’applicazione al baricentro della sfera di una forza totale (Gravità+Ercole) con direzione appena più … orizzontale di quella che individua la direzione dello spigolo del gradino.
Chiamo con α l’angolo (con vertice nel centro della sfera) formato dalla verticale e dalla direzione dello spigolo del gradino.
Posso scrivere che: R-h = R*cosα
da cui: cosα = (R-h)/R
Posso anche scrivere che: R*sinα = [R^2 – (R-h)^2]^0,5
So che: tgα = sinα/cosα = (5)^0,5/2
La condizione cercata è allora:
Fe = Fp*tgα = 500*(5)^0,5/2 = 250*(5)^0,5 = 559 kgp
dove Fe è la forza minima che Ercole deve applicare.
Per Herculem che quiz!!!
Scusa Enzo per la fretta, provo a spiegarmi: Ho considerato la sfera appoggiata istantaneamente su un ipotetico piano inclinato con angolo alla base uguale all'angolo tra la verticale (linea di applicazione della forza-peso) e la congiungente tra centro della sfera e punto di contatto sul gradino. L'angolo, il cui coseno è 2:3 = 0,666666, risulta 48,19°.
Ho scomposto i 500 Kg (verticali) secondo le direzioni di spinta e di contatto sul gradino.
F = 500 x tg 48,19° = 500 x 1,118 = 559 Kg
mentre sulla punta del gradino si scaricano 750 Kg (500 : cos 48,19°).
Appena in movimento, l'angolo si riduce e quindi anche la forza, fino ad annullarsi quando il centro sfera raggiunge la verticale della punta del gradino (3 x sen 48,19° = 2,24 m).
(Essendo l'angolo maggiore di 45°, non mi sembra una situazione molto conveniente..... forse Ercole farebbe bene a cambiare direzione di spinta ....).
O sbaglio ?
Ops, scusate, la forma corretta è
la forma corretta è
PER HERCULEM, QUOD QUAESTIO!
mannaggia all'inglese fuori luogo!!
Caro LuigiS, ho provato a disegnare una situazione diversa con Ercole che, anzichè spingere in orizzontale, spinge in senso obliquo, dal basso verso l'alto, con inclinazione di 45°. Immaginiamo allora un vettore Fe inclinato di 45° applicato nel baricentro della sfera: l'intensità sia quella già trovata di 559 kgp.
Si vede che il vettore somma (Ercole+Gravità) è più ... orizzontale di quello della soluzione ma più corto: possiamo pensare che sia composto dalla somma del vettore Fe della soluzione e da un secondo vettore Fx.
Questo secondo vettore Fx ha una componente verticale ed una orizzontale VERSO SINISTRA. La componente orizzontale è ... fatica sprecata, mentre quella verticale (orientata verso l'alto) ... pure, perchè costringe Ercole a sollevare il masso più di quanto occorra!
Per il disegnino dei vettori ci vorrebbe il grande Paolo che è uno specialista.
Mi sembra però che la spinta orizzontale sia quella più conveniente.
Non dico ancora niente di preciso, ma devo confermare Alvy. La spinta orizzontale è sicuramente la migliore... tutto il resto è fatica sprecata. Basterebbe pensare a come funziona il momento di una forza (e noi di questo abbiamo bisogno) e si ha subito che quella che ha importanza è solo la componente orizzontale!
Ma ercole una bella gru non poteva usarla?!?! subito a utilizzare la forza bruta!!
A me pare che se Ercole spingesse obliquamente, dal basso verso l'alto, con un'inclinazione di 48,19° potrebbe bilanciare il peso della sfera con 373 Kg di spinta (500 x sen 48,19°) e sulla punta del gradino si scaricherebbero 333 Kg (500 x tg 48,19°).
Non so come fare ad allegare il mio schizzo della scomposizione della forza.
E purtroppo da stasera sarò senza computer per un po' di tempo ... ma un giorno controllerò la correzione.
Scusate e grazie
In realtà, la domanda si riferiva alla figura riportata nel quiz: forza orizzontale e centrale. Le soluzioni potrebbero essere diverse se la forza fosse applicata in punti più alti e con certe inclinazioni. Rimaniamo, però, nell'esempio più semplice... già così le risposte latitano... Vorrei commentare questo fatto...
Hercules dovrebbe farsi un giretto su Papalla! Ha scelto la meno efficace delle opzioni...
Anni e anni di esperienza come pilota di passeggini e carrelli della spesa insegnano che di fronte a un gradino è inutile spingere, bisogna alzare!
Dimostriamolo...
Sia A il punto in cui la sfera poggia sul gradino, T il punto di contatto con il terreno, B il punto in cui verrà applicata la forza F (dall'altro lato di A rispetto a T) ed infine C il punto del diametro 2r passante per il centro O ed opposto ad A (fatto su un disegno è molto più facile da vedere...).
Calcoliamo il segmento di corda AB. Sia (alfa) l'angolo in A compreso fra il diametro AC e la corda AB. AB sarà quindi AC*cos(alfa) ossia 2r*cos(alfa). Applicando in B una forza ortogonale alla corda AB (quindi diretta verso C essendo il triangolo ABC retto in B perchè angolo alla circonferenza) si ha il Momento della forza che agisce sul punto A, ossia M=F*2r*cos(alfa). Per spingere la sfera oltre il gradino tale Momento deve risultare maggiore del Momento esercitato dalla forza di gravità. Andremo perciò a scrivere F*2r*cos(alfa)>Mg*r.
volendo trovare la forza F abbiamo F>Mg*r/2r*cos(alfa) e semplificando F>Mg/2cos(alfa).
Vediamo subito che il denominatore è maggiore di 1 per valori di (alfa) minori di 60° e quindi è necessaria una forza più piccola man mano che AB tende a AC.
Facciamo quindi la classifica dell'efficia di F:
1) Forza normale (nel senso di ortogonale) ad AB applicata nel punto B;
2) Sollevamento brutale della sfera per posarla sul basamento;
3) Spinta orizzontale.
Ricordiamoci sempre che Ercole è un uomo ed è più facile esercitare un forza orizzontale che non dal basso verso l'alto... Insomma, perché dobbiamo complicare la vita al povero Ercole? Comunque, domani o dopodomani, riportando la soluzione, vediamo se si può fare di meglio... Ad esempio, sollevare la sfera può anche andar bene, ma bisogna anche spingerla per superare il gradino... E, inoltre, la forza di uno che solleva non è la stessa di uno che spinge.
aggiungo anche che imprimere una forza che non passi per il centro della sfera vuole dire esercitare una coppia che fa ruotare la ruota attorno a un certo asse che poco ha a che fare col sollevamento oltre al gradino. L'approccio di Celterman, però, vale la pena di essere studiato con calma e lo farò sicuramente. Scusate ma in questi giorni siamo in pieno caos, per preparare tutto per il ritorno a casa di nostra figlia...
caro Celterman,
ho avuto 5 minuti di tempo... e temo che tu abbia commesso un errore. La forza DEVE passare per il centro della sfera. Immagina di portare tutta la sfera nel suo baricentro. Il momento deve avere come braccio AO. I casi da te riportati hanno solo una piccola componente che va nel verso giusto... Insomma, la forza da applicare (non orizzontale, come invece diceva il quiz), deve passare sempre per il centro della sfera e poi va calcolato il momento... che causa la rotazione attorno a O...
Domani cerco di spiegarmi meglio....
Non credo che sia necessario, se l'asse passa per O la forza F è la minima che si possa applicare, per gli altri casi è superiore, ma sempre meno delle altre 2 opzioni.
Inoltre per spingere agevolmente sull'asse CA passante per O, dovrebbe essere alto almeno 3 Giacobbo...
Caro Celterman,
la forza deve passare per il centro di massa se si vuole che si ottenga una rotazione attorno al punto B. Come già detto, il problema deve potersi ridurre al caso di una sfera puntiforme di pari massa concentrata nel baricentro. Nei casi non centrali questo non dà risultato...
La soluzione, inoltre deve tener conto che la forza impartita non solo faccia ruotare per superare lo scalino, ma spinga in avanti per continuare il moto.
Insomma, la situazione diventerebbe completamente diversa da quella originaria. Mi limiterò quindi a dare la soluzione per il caso della figura: forza agente in verso orizzontale.
E poi... non sapevi che Ercole è alto esattamente tre metri???

La rotazione (ma è improprio parlare di rotazione) deve avvenire nel punto A (il fulcro), non in B. È il principio della leva, solo che in questo caso la leva è integrata e non esterna.
Non riesco mai a spiegarmi, ma non c'è il modo di allegare qualche immagine?
P.S. Perciò è alto solo un Giacobbo e mezzo?
P.S.2 Non è molto efficace spingere da una altezza superiore a quella delle spalle... Gran parte della spinta andrebbe persa... Ricorda che la sfera è alta sei metri...
caro Celterman,
è possibile che non ci si possa limitare solo all'esercizio in questione con i dati e le condizioni scelte? Mi sembra che le poche risposte indichino che per adesso basti e avanzi. Su, abbi pazienza... e aspetta il prossimo quiz...
sì, sì, il punto era A e non B... ossia il centro della rotazione... li ho confusi...
Tuttavia, un metodo per mandare disegni c'è (Paolo lo fa sempre e potrebbe dirti come fa...). Comunque, resta la richiesta di evitare ulteriori complicazioni... OK? Se esiste un momento angolare esiste una rotazione... perché no?
Ok, no problem!
Lo so che il quiz era diverso, era solo un modo di esplorare le alternative dato che le risposte convenzionali erano già arrivate...