Torniamo alla trasformazione “canonica” e vediamo di ricavare, direttamente da lei, quali sono i fenomeni apparentemente assurdi che riesce a produrre. Già sappiamo che un sistema in movimento pone non pochi problemi alla sincronizzazione degli orologi che sembra giusta o sbagliata a seconda di dove si cerchi di verificarla. Non possiamo, perciò, stupirci più di tanto se il tempo e lo spazio diventano qualcosa di … relativo.

Due fattori fondamentali

Prima di partire in quarta, è utile prendere maggiore dimestichezza con i due parametri adimensionali β e γ che abbiamo introdotto la volta scorsa. Essi sono fondamentali per capire al meglio a cosa si va incontro. Il primo ci dice chiaramente quanto sia veloce il nostro sistema di riferimento che si muove di moto rettilineo uniforme rispetto a un altro. Infatti, non è altro che il rapporto tra la velocità relativa e quella della luce. E’, allora, interessante vedere come γ, molto meno intuitivo, varia in funzione di β. Potrebbe essere un semplice esercizio di studio di funzione dato che abbiamo:

γ = 1/(1 – β²)^1/2

dove β fa la parte della x e γ quella della y. E’ una funzione che vede una radice quadrata, in cui compare il quadrato di x, al denominatore. Stiamo parlando di relatività ristretta e sembrerebbe puerile parlare di funzioni elementari, ma noi cerchiamo di non perdere mai di vista una visione globale di ciò di cui discutiamo. Invito, perciò, chi vuole imparare meglio il calcolo delle derivate, di trovare i possibili massimi e/o minimi della funzione.

A noi interessa mostrare il risultato finale per avere un’idea di come il parametro γ vari con β, ossia con la velocità del moto relativo riferita alla costante c (velocità della luce). Per semplicità, possiamo considerare solo valori positivi di v (il risultato non cambia per valori negativi, dato che la velocità compare al quadrato). Il valore minimo di v è quindi ZERO, ossia abbiamo sistemi fermi uno rispetto all’altro. Per v = 0, anche β = 0 e γ = 1. Il valore massimo “plausibile” per v è dato da c, ossia β = 1. Questo valore comporta γ = + ∞. La funzione, perciò, tende a infinito (positivo) per v che tende a c. La curva risultante è riportata in Fig. 1

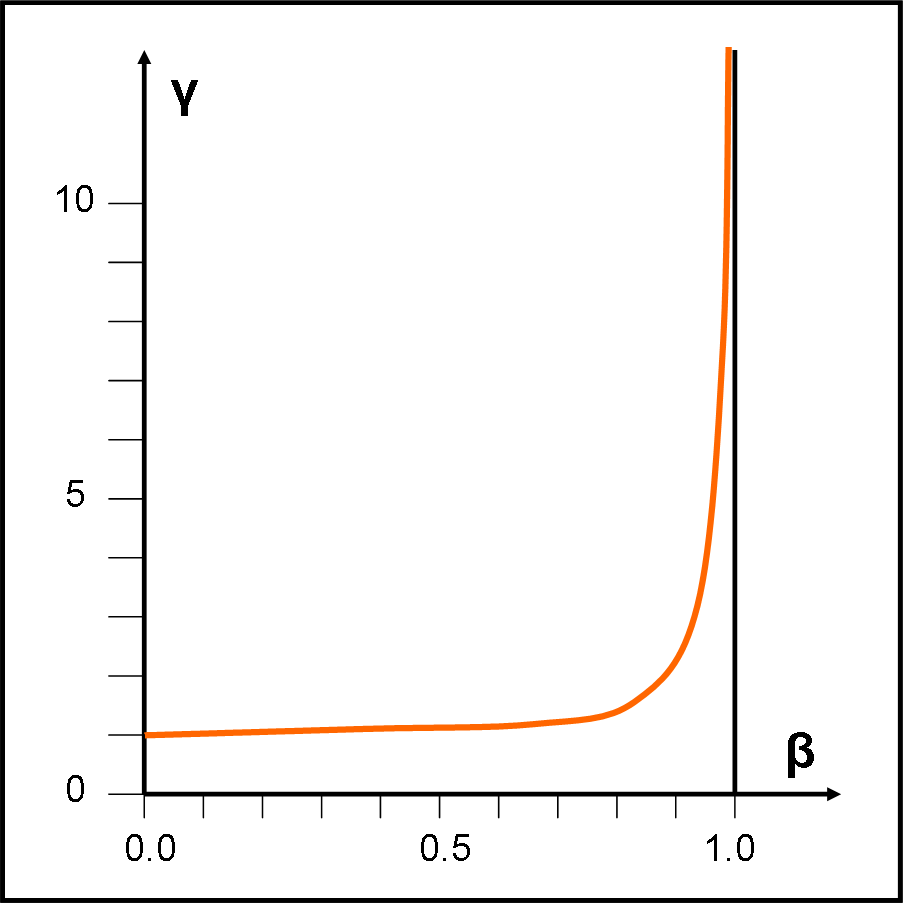
Si nota molto bene che per valori anche grandi di v (e quindi di β) il valore di γ si discosta poco da 1. In altre parole, guardando la trasformazione di Lorentz relativa alla x, si ha che x’~ x – vt, ossia si ricade nella trasformazione galileiana.

La fisica di tutti i giorni, quella che ci circonda, si svolge praticamente tutta in questo ambito. Pensiamo a un aereo supersonico che viaggi a 3600 km/h, ossia 1 km/sec. Niente male anche per l’uomo “normale” del 2015. Eppure, in questo caso avremmo β = 1/300 000 = 0.00000333... che porta a un valore di γ = 1.0000000000055. Pochi strumenti potrebbero rendersi conto della differenza tra questo valore e quello “galileiano” perfettamente uguale a 1.

Per valori di v prossimi a quelli della luce, però, γ parte come una “scheggia” e tende rapidamente a infinito. Per v > c (valore  matematicamente plausibile) avremmo una radice quadrata negativa e γ perderebbe di significato. La faccenda non ci disturba affatto, dato che nessun corpo dotato di massa può raggiungere o superare la velocità della luce. La figura precedente ci mostra matematicamente che la velocità della luce è un limite insuperabile.

Tuttavia, l’intero microcosmo, il “nocciolo” concettuale di tutta la fisica macroscopica, vive muovendosi a velocità molto prossime a c. Ne segue che la relatività ristretta è fondamentale per descriverlo correttamente. Oggi che siamo capaci di arrivare vicino a c anche nei laboratori terrestri, la relatività ristretta diventa dominatrice di moltissimi fenomeni, insieme alla sua sorella maggiore relatività generale e alla nuova e scomoda arrivata, la meccanica quantistica. Insomma, per vedere veramente in grande bisogna guardare sempre più verso il piccolo. E dispiace sempre di più che per sentir parlare di questi tre "giganti" della fisica è necessario, spesso, arrivare all'Università...

Applichiamo la trasformazione

Bando alle “ciance” e torniamo alla nostra trasformazione e ai suoi effetti più evidenti. Teniamo ben presente il legame tra v/c e il fattore di Lorentz, dato che β ci dice praticamente la velocità a cui viaggia il sistema in movimento relativo e γ ci quantifica i suoi effetti sul tempo e la lunghezza.

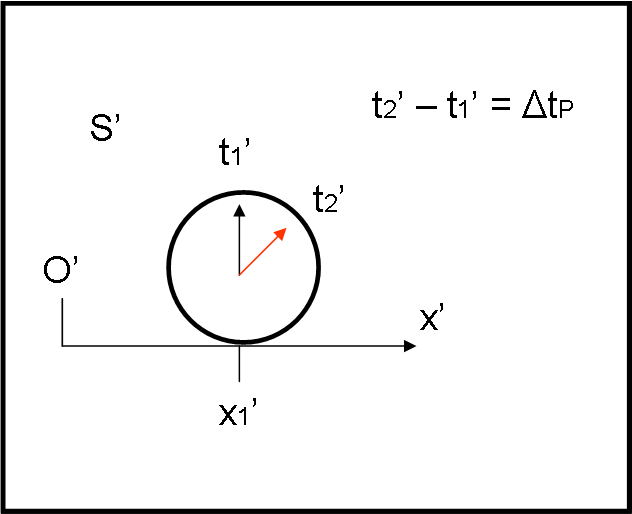
Consideriamo, in Fig. 2, un sistema di riferimento S’ di origine O’. Poniamo un bell’orologio C’ su di esso, a una distanza fissa x₁’ dall’origine.

Facciamolo partire e guardiamolo girare. L’orologio, trovandosi sempre nella stessa posizione rispetto all’origine, segnerà esattamente il tempo misurato in quel punto. Vi sembra che stia dicendo una banalità quasi ridicola? Bene, pazienza… ma teniamola bene a mente: stiamo misurando un tempo sempre dallo stesso punto fisso, quello in cui si trova l’orologio. Segniamo l’ora in un dato momento t₁’.  Lasciamolo girare per qualche minuto e leggiamo di nuovo l’ora: essa è quella relativa al tempo t₂’. Attenzione: sia t₁’ che t₂’ sono stati misurati, con lo stesso orologio, sempre nello stesso punto, quello in cui si trova l’orologio. Non vi è stato bisogno di eseguire nessuna sincronizzazione. In altre parole sia t₁’ che t₂’ sono stati misurati nella posizione fissa  x₁’ del sistema S’. La differenza tra i due tempi misurati in questo modo (ossia lo scorrere del tempo misurato su uno stesso orologio in uno stesso punto) lo indichiamo in un modo speciale, ossia:

Δt_P = t₂’ – t₁’

Scendiamo dal sistema S’ e portiamoci su un altro sistema S di origine O (Fig. 3).

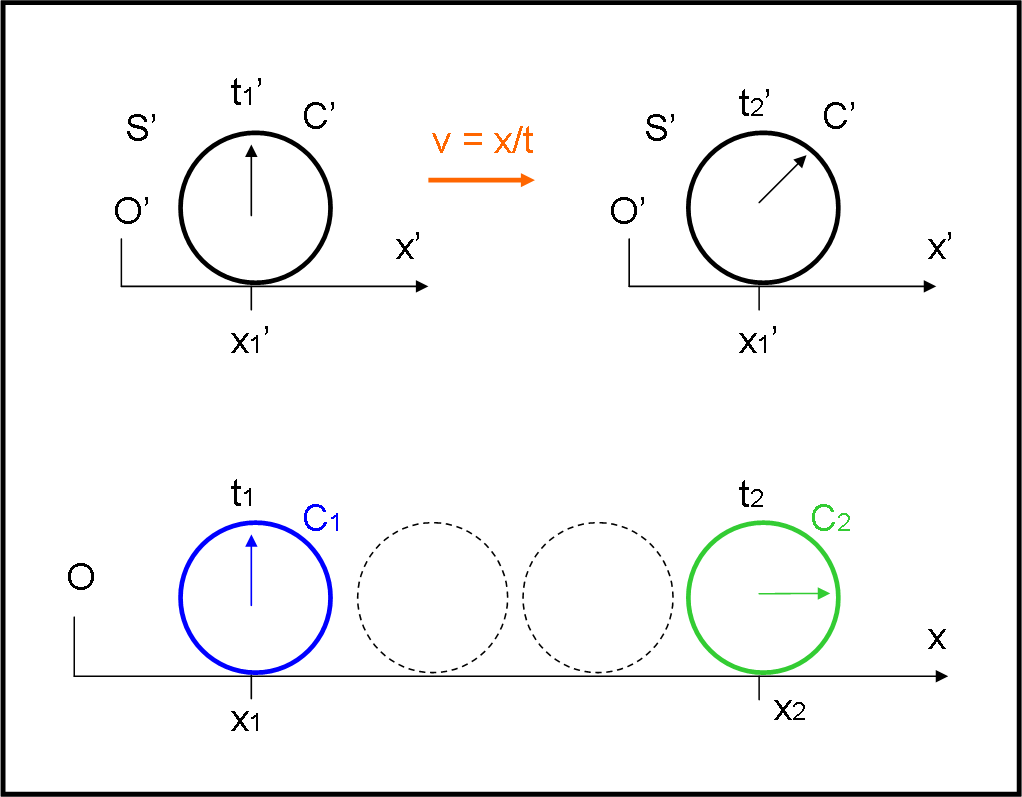
Lungo l’asse x di S si sono posizionati moltissimi orologi, tutti sincronizzati tra loro (ma sappiamo quanto la sincronizzazione sia relativa…). Ci accorgiamo che , in realtà, il sistema S’, in cui avevamo misurato quel tempo così speciale, è in movimento rispetto a S con velocità uguale a v. Da questa posizione “esterna”  vediamo passare l’orologio C’ nel punto di coordinate x₁ (del sistema S). Quando C’ segna t₁’, viene misurato il tempo t₁ attraverso l’orologio C₁ posizionato in x₁. Il tempo passa e il sistema S’ con il suo orologio C’ scorre verso destra rispetto a S. Nel momento in cui l’orologio C’ segna il tempo t₂’, utilizziamo l’orologio C₂ posto nella posizione x₂ per misurare t₂. Attenzione! Ci siamo fidati ciecamente della sincronizzazione dei due orologi C₁ e C₂ posti in due punti x₁ e x₂, diversi, del sistema S.

Tuttavia, sappiamo che questa sincronizzazione non è valida per tutti i sistemi in movimento tra loro… Ne vediamo subito gli effetti, utilizzando la trasformazione tra t e t’ che abbiamo ricavato solo e soltanto attraverso i postulati di Einstein. Ribadiamo ancora la netta differenza tra i tempi t₁’ e t₂’, misurati sullo stesso orologio posto sempre nello stesso punto x₁’ del sistema S’ e i tempi t₁ e t₂, misurati  su due orologi diversi posti in punti diversi del sistema S.

Questo è il punto fondamentale della relatività ristretta, espressa matematicamente dalla trasformazione di Lorentz.

Ricapitoliamo, facendo uscire allo scoperto la relazione che lega t e t’.

t’ = (t – vx/c²)/(1 – v²/c²)^1/2

Riferiamola al momento in cui l’orologio C’ segna t₁’ e  quello C₁, posto in x₁ segna t₁:

t₁’ = (t₁ – vx₁/c²)/(1 – v²/c²)^1/2     …. (1)

Riferiamola, adesso, al momento in cui l’orologio C’ segna t₂’ e quello C₂, posto in x₂ segna t₂.

t₂’ = (t₂ – vx₂/c²)/(1 – v²/c²)^1/2     …. (2)

Per vedere come scorre il tempo non dobbiamo fare altro che fare la differenza tra la (2) e la (1)

t₂’ - t₁’ = (t₂ – vx₂/c² – t₁ + vx₁/c²)/(1 – v²/c²)^1/2  = ((t₂ - t₁) – v(x₂ – x₁)/c²)/(1 – v²/c²)^1/2

Chiamiamo Δx la differenza tra x₂ e x₁ e Δt la differenza tra t₂ e t₁ (misurati con orologi diversi posti in punti diversi). Δt_P sappiamo già cos’è.

Δt_P = (Δt – vΔx/c²)/(1 – v²/c²)^1/2

Ma  Δx = vΔt , per definizione di velocità costante misurata nel sistema S.

E, quindi:

Δt_P = (Δt – Δt v²/c²)/(1 – v²/c²)^1/2  = Δt (1 –v²/c²)/(1 – v²/c²)^1/2 = Δt (1 – v²/c²)^1/2

E, infine:

Δt = Δt_P/(1 – v²/c²)^1/2 = γ Δt_P

Ossia:

Δt = γ Δt_P            …. (3)

 

Fantastico e semplicissimo risultato: la differenza di tempo misurato attraverso i due orologi posti in punti diversi di S è legata alla differenza di tempo, misurata attraverso un unico orologio posto nel punto fisso x’ di S’, solo attraverso il fattore di Lorentz!

Il tempo proprio non cambia

Sappiamo, però, benissimo che il fattore γ rimane sempre maggiore di 1, a mano a mano che la velocità relativa aumenta. Questo vuol dire che il tempo segnato da un orologio che si muove con velocità v appare andare sempre più lento rispetto a quello misurato dagli orologi posti in un sistema che si considera fermo. Facciamo attenzione che la stessa identica cosa accadrebbe se S’ si considerasse fermo e volesse misurare il tempo che scorre sul sistema S in movimento con velocità –v rispetto a lui. In queste condizioni l’orologio fisso sarebbe quello in S e gli orologi differenti apparterebbero a S’. A S’ sembrerebbe che il tempo di S scorra più lentamente del suo. Esattamente la stessa cosa che dice S. La trasformazione è sempre la stessa, con l’accortezza di cambiare v in –v.

Proprio da questa simmetria, insita nella relatività ristretta, nasce il ben noto paradosso dei gemelli.

Per comprenderne appieno il significato, ripetiamo ancora il risultato ottenuto: l’intervallo di tempo Δt che viene misurato nel sistema di riferimento in cui l’orologio C’ viene visto muoversi con velocità v è sempre maggiore del valore Δt_P misurato dall’orologio C’. Questo risultato è quello che viene comunemente chiamato dilatazione relativistica del tempo.

Come già accennato c'è una differenza sostanziale fra gli intervalli di tempo Δt_P  e Δt che appaiono nella (3). L'intervallo di tempo Δt_P, infatti, è il tempo misurato da un unico orologio C’ e, quindi, non è in nessun modo influenzato dalle procedure di sincronizzazione. Questo tempo è, quindi,  una grandezza fondamentale  di tutta la teoria e viene chiamato  TEMPO PROPRIO. L'intervallo di tempo Δt, invece, è quello misurato da due orologi diversi (C₁ e C₂), posti in punti diversi di posizione x₁ e x₂, e, quindi, dipende fortemente da come gli orologi del sistema S sono stati sincronizzati fra di loro.

Non dobbiamo, perciò, travisare il concetto di tempo dilatato per chi viaggia a una certa velocità v rispetto a noi. Il suo tempo, misurato all’interno del sistema, è quello proprio. Esso appare scorrere più lentamente solo se “osservato” dal nostro sistema di riferimento che lo vede muoversi con velocità v. Questo effetto appare identico a quello che misura un osservatore del sistema S’ mentre ci vede muovere con velocità uguale e opposta –v.

A questo punto, capite molto bene perché è stato più giusto iniziare con il concetto di sincronizzazione degli orologi su un certo sistema di riferimento e della sua relatività rispetto a sistemi in moto tra di loro. Ciò ci ha indotto a pensare che il tempo non potesse essere assoluto ma relativo. Attraverso l’utilizzo dei soli postulati di base abbiamo ricavato la trasformazione di coordinate che lega i due sistemi di riferimento. L’abbiamo infine applicata a un caso reale, verificando matematicamente il concetto che la sincronizzazione relativistica ci aveva suggerito.

Il semplice fatto che v = x/t ci dice subito che se t è relativo al sistema di riferimento e v è una costante, deve essere relativa anche la lunghezza x. Lo vedremo nel prossimo articolo…