QUIZ: la rigorosa meccanica papalliana**
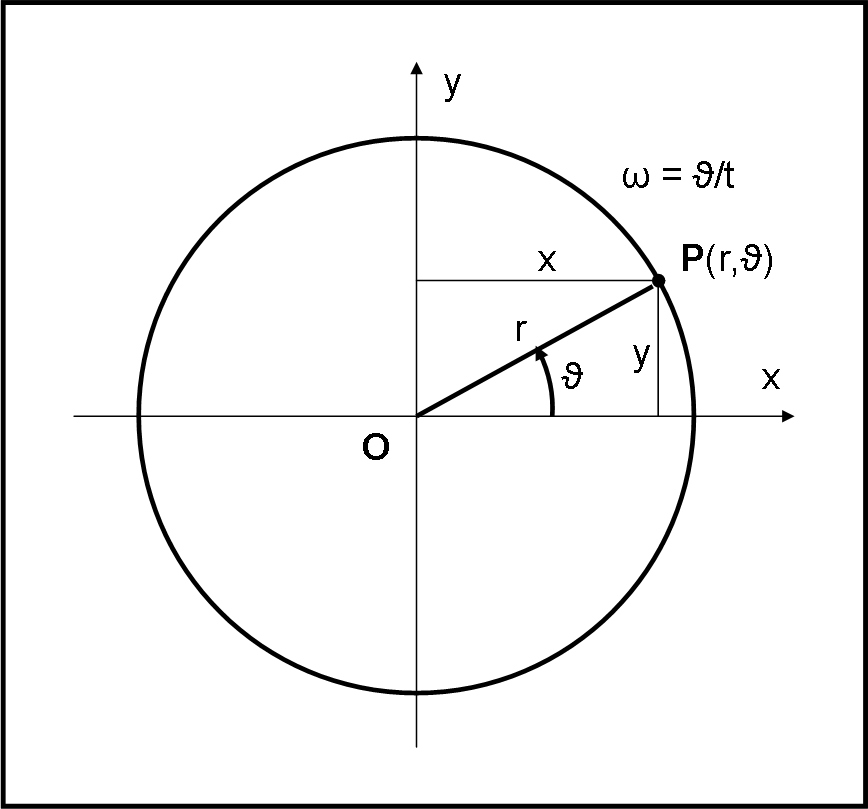
Il problema è molto semplice. Papallino P ruota attorno al punto O con velocità angolare costante. Ricordiamo che la velocità angolare, analogamente alla velocità lineare che conosciamo molto bene, è data dall’angolo descritto nell’unità di tempo, ossia ω = ϑ/t. Su Papalla usano solo le coordinate polari per determinare la posizione di un punto (dovreste ricordarle…).
Ciò che si domanda è : “Determinare la posizione di papallino P rispetto a O, la sua velocità lineare la sua accelerazione, in coordinate polari (r,ϑ). Dimostrare, inoltre, che quest’ultima è sempre diretta verso il centro O”.
Il problema è veramente facile, ma comporta l’utilizzo dei versori i e j relativi a x e y. Abbiamo spesso usato la formula finale dell’accelerazione, ma sempre calcolata in modo “approssimato”. E’ giunta l’ora di ricavarla in modo rigorosamente papalliano, utilizzando vettori, versori e derivate…
Ci si può anche divertire allargando il discorso a percorsi curvilinei qualsiasi…
N.B.: l’esercizio serve anche a capire molto bene come mai una velocità costante per definizione può dar luogo a un’accelerazione che non è uguale a zero. Sembrerebbe impossibile, dato che l’accelerazione è la derivata della velocità e la derivata di una costante dovrebbe essere uguale a zero! Ne segue che i vettori diventano indispensabili.






13 commenti
Visto che nessuno si propone Enzo, ho deciso di dare seguito allo sviluppo del quiz tirando in ballo il moto a curvatura variabile.
Inizio dalla generica posizione del punto P in coordinate polari:
Xp = R*cosθ*I
Yp = R*sinθ*J
d(Xp) = (dR*cosθ-R*sinθ*dθ)*I
d(Yp) = (dR*sinθ+R*cosθ*dθ)*J
V(Xp) = [(dR*cosθ-R*sinθ*dθ)/dT]*I
V(Yp) = [(dR*sinθ+R*cosθ*dθ)/dT]*J
V(Xp) = [(dR*cosθ-R*sinθ*dθ)/dT]*I = (dR*cosθ/dT + VXpc)*I
V(Yp) = [(dR*sinθ+R*cosθ*dθ)/dT]*J = (dR*sinθ/dT + VYpc)*J
Si vede come alle componenti della velocità VXpc*I, VYpc*J (componenti della velocità nel moto circolare uniforme) si aggiungono due contributi che dipendono da quanto velocemente varia R con il tempo: per dR=0 si torna al moto circolare uniforme.
Il vettore velocità risultante avrà quindi direzione diversa da quella del moto circolare.
Possiamo anche scrivere:
V(Xp) = (dR*cosθ/dT + VXpc)*I = (VR*cosθ + VXpc)*I
V(Yp) = (dR*sinθ/dT + VYpc)*J = (VR*sinθ + VYpc)*J
Il modulo del vettore V vale ora:
V = √[VR^2+2*VR*(cosθ*VXpc+sinθ*VYpc)+VXpc^2+VYpc^2]
ovvero:
V = √[VR^2+2*VR*(cosθ*VXpc+sinθ*VYpc)+Vpc^2]
-----------------------------------------------------------------
Per l’accelerazione:
dV(Xp) = (dVR*cosθ - VR*sinθ*dθ + dVXpc)*I
dV(Yp) = (dVR*sinθ + VR*cosθ*dθ + dVYpc)*J
da cui, dividendo per dT:
A(Xp) = (AR*cosθ – VR*sinθ*ω + AXpc)*I
A(Yp) = (AR*sinθ + VR*cosθ*ω + AYpc)*J
Per semplicità accettiamo l’idea che VR = cost. e quindi AR = 0.
Otteniamo che:
A(Xp) = (– VR*sinθ*ω + AXpc)*I
A(Yp) = (+ VR*cosθ*ω + AYpc)*J
Il modulo del vettore A vale ora:
√[AXpc^2+(VR*sinθ*ω)^2-2*AXpc*VR*sinθ*ω]+[AYpc^2+(VR*cosθ*ω)^2+2* AYpc*VR*cosθ*ω],
ovvero:
√[AXpc^2+AYpc^2+(VR*ω)^2+2*VR*ω*(AYpc*cosθ - AXpc*sinθ)]
A = √[Apc^2 +(VR*ω)^2+2*VR*ω*(AYpc*cosθ - AXpc*sinθ)]
In questo caso il modulo dell’accelerazione è costituito dall’accelerazione centripeta che compete al moto circolare uniforme (Apc) a cui si aggiungono altri termini in cui compare la velocità radiale VR: se questa si annulla si torna al moto circolare uniforme.
Sarebbe interesssante vedere cosa accade imponendo alcune condizioni peculiari.
Magari ci penso su ...
Non sono sicuro di aver capito bene bene bene,
ma vediamo di dire qualcosa...
La posizione del papallino si potrebbe già evincere sia dalla figura che dal testo, ma noi lo vogliamo calcolare in qualsiasi istante t. Quindi P(r, ϑ) diventa P(r, ωt), dove ω è la velocità angolare;
la velocità lineare (che è la distanza percorsa dal punto P nell'unità di tempo) si può esprimere come v=ω.r = 2π.r/T = r. ϑ/t - Dove T è il periodo di rotazione completa, ϑ l'angolo percorso all'istante t;
L’accelerazione...
E qui si complica un po’...
La spiegazione più semplice:
Consideriamo le due componenti l’accelerazione in un moto curvilineo:
l’accelerazione radiale (o centripeta) – che chiameremo ac
l’accelerazione tangenziale (o traversa) -– che chiameremo at.
Nel moto circolare uniforme at=0, quindi resta solo la componente ac.
Quella un po’ meno semplice (dato che parlavi di versori e derivate, vediamo di accontentarti!):
sia dato il versore di v nel punto P, ossia il vettore con modulo unitario che condivide con v direzione e verso (si ottiene dividendo il vettore v per il suo modulo, Ve=v/|v|)
Sia perciò Ve(t) un versore dipendente dal tempo t. Proviamo a fare un po’ di passaggi:
Eseguiamo il prodotto scalare del versore per se stesso:
Ve.Ve=|Ve|^2
Poiché i versori hanno modulo unitario:
Ve.Ve=1
Da questa, derivando membro a membro:
Ve’.Ve + Ve.Ve’=0
2(Ve’.Ve)=0
Ve’.Ve=0
poiché il prodotto scalare Ve’.Ve deve essere uguale a zero, la derivata di un versore deve essere perpendicolare al versore stesso.
caro Celty... è necessario che tu parta dal vettore distanza r e lo scrivi in base alle sue coordinate polari riferite ai due versori i e j. Poi basta fare le derivate successive...
Ci sono molti modi per trovare il risultato, ma mi piaceva che si seguisse quello in coordinate polari e con i versori...
Perdonami, sono un po' indisciplinato...
Purtroppo a volte mi lascio un po' prendere la mano e vado fuori tema...
Faccio ora qualche ipotesi, sempre nel caso che la traiettoria sia spiraliforme, ovvero a raggio variabile.
PER LA VELOCITA’
Ponendo θ=0° otteniamo che:
V(Xp) = (dR*cosθ/dT + VXpc)*I = (VR*cosθ + VXpc)*I
V(Yp) = (dR*sinθ/dT + VYpc)*J = (VR*sinθ + VYpc)*J
e
V = √[VR^2+2*VR*(cosθ*VXpc+sinθ*VYpc)+VXpc^2+VYpc^2]
diventano:
V(Xp) = (dR/dT + VXpc)*I = (VR + VXpc)*I
V(Yp) = (VYpc)*J
e, quindi:
V = √[VR^2+2*VR*(VXpc)+VXpc^2+VYpc^2]
ovvero:
V = √[VR^2+2*VR*(VXpc)+Vpc^2]
Si vede come il contributo verticale alla velocità totale rimane quello del moto circolare VYpc, mentre il contributo orizzontale si arricchisce del termine VR dovuto alla velocità con cui cambia la distanza di P dal centro di rotazione.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Ponendo θ=90° otteniamo invece che:
V(Xp) = (dR*cosθ/dT + VXpc)*I = (VR*cosθ + VXpc)*I
V(Yp) = (dR*sinθ/dT + VYpc)*J = (VR*sinθ + VYpc)*J
e
V = √[VR^2+2*VR*(cosθ*VXpc+sinθ*VYpc)+VXpc^2+VYpc^2]
diventano:
V(Xp) = (VXpc)*I
V(Yp) = (dR/dT + VYpc)*J = (VR + VYpc)*J
e, quindi:
V = √[VR^2+2*VR*(VYpc)+VXpc^2+VYpc^2]
ovvero:
V = √[VR^2+2*VR*(VYpc)+Vpc^2]
Si vede come il contributo orizzontale alla velocità totale rimane quello del moto circolare VXpc, mentre il contributo verticale si arricchisce del termine VR dovuto alla velocità con cui cambia la distanza di P dal centro di rotazione.
In pratica,
essendo il vettore velocità tangente alla traiettoria, la nuova traiettoria è determinata, punto per punto, dal valore della velocità radiale (imposta dalla continua variazione di R) che si somma al vettore velocità associato al moto circolare nel punto.
Quando P si trova sull’asse delle X (θ=0°) la componente radiale è diretta orizzontalmente. Quando P si trova sull’asse delle Y (θ=90°) la componente radiale è diretta verticalmente, come ovvio.
Nelle condizioni intermedie (0°<θ<90°) la componente radiale della velocità sarà diretta lungo la congiungente il centro di rotazione (istantaneo) con P.
-----------------------------------------------------------------
PER L’ACCELERAZIONE, sempre con VR=cost e AR=0.
Ponendo θ=0° otteniamo che:
A(Xp) = (– VR*sinθ*ω + AXpc)*I
A(Yp) = (+ VR*cosθ*ω + AYpc)*J
e
A = √[Apc^2 +(VR*ω)^2+2*VR*ω*(AYpc*cosθ - AXpc*sinθ)]
diventano:
A(Xp) = (AXpc)*I
A(Yp) = (VR*ω + AYpc)*J
e, quindi:
A = √[Apc^2 +(VR*ω)^2+2*VR*ω*(AYpc)]
Si vede come il contributo orizzontale all’accelerazione totale rimane quello del moto circolare AXpc, mentre il contributo verticale si arricchisce del termine VR*ω dovuto alla velocità con cui cambia la distanza di P dal centro di rotazione.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Ponendo θ=90° otteniamo invece che:
A(Xp) = (– VR*sinθ*ω + AXpc)*I
A(Yp) = (+ VR*cosθ*ω + AYpc)*J
e
A = √[Apc^2 +(VR*ω)^2+2*VR*ω*(AYpc*cosθ - AXpc*sinθ)]
diventano:
A(Xp) = (– VR*ω + AXpc)*I
A(Yp) = (AYpc)*J
e, quindi:
A = √[Apc^2 +(VR*ω)^2+2*VR*ω*(- AXpc)]
Si vede come il contributo verticale all’accelerazione totale rimane quello del moto circolare AYpc, mentre il contributo orizzontale si arricchisce del termine -VR*ω dovuto alla velocità con cui cambia la distanza di P dal centro di rotazione.
La questione m'incuriosiva, ma giuro che la pianto qui, anche perchè devo fare i conti con la mia ignorantitudine!
Naturalmente se ho scritto delle enormità sono disponibile a punizioni corporali
caro Alvy... direi che ci starebbe bene l'accelerazione di Coriolis...
GRANDISSIMO ENZONE!!!

Sei davvero un artista!
Come cavolo ho fatto a non evidenziarla!!
ACCELERAZIONE di CORIOLIS
Un corpo in moto in un riferimento non inerziale rotante avverte un’accelerazione, detta di Coriolis, pari a:
Ac = -2*VΛω
Dove V è la velocità del corpo ed ω la velocità angolare del sistema rotante. La direzione è ovviamente ortogonale ad entrambi i vettori in causa (V; ω).
Il segno negativo indica che per ricavare il senso del vettore bisogna applicare la regola della mano … sinistra!
Riprendiamo ora le formule generali dell’accelerazione, avendovi già posto VR=cost e AR=0:
A(Xp) = (– VR*sinθ*ω + AXpc)*I
A(Yp) = (+ VR*cosθ*ω + AYpc)*J
e:
A = √[Apc^2 +(VR*ω)^2+2*VR*ω*(AYpc*cosθ - AXpc*sinθ)]
Possiamo riscriverle facendovi comparire l’accelerazione di Coriolis AC:
A(Xp) = (+ sinθ*AC/2 + AXpc)*I
A(Yp) = (- cosθ*AC/2 + AYpc)*J
e
A = √[Apc^2 + AC/4 - Ac*(AYpc*cosθ - AXpc*sinθ)]
Conclusione:
Le formule sono state impostate e scritte considerando il punto di vista di un osservatore inerziale (fermo o in moto rettilineo uniforme).
Nel caso di moto circolare uniforme si era ricavato che:
AXp = -R*ω^2*cosθ*I (5)
AYp = -R*ω^2*sinθ*J (6)
e, quindi:
A = -R*ω^2*cosθ*I-R*ω^2*sinθ*J = (R*ω^2)*(-cosθ*I-sinθ*J)
Le voglio riscrivere facendovi comparire l’accelerazione centrifuga AF (forza fittizia avvertita dal papallino non inerziale, come l’accelerazione di Coriolis in caso di moto nel sistema non inerziale):
AXp = -AF*cosθ*I (5’)
AYp = -AF*sinθ*J (6’)
e, quindi:
A = -AF*cosθ*I-AF*sinθ*J = AF*(-cosθ*I-sinθ*J)
Questo vettore è diretto radialmente e rappresenta l’accelerazione centripeta vista dall’osservatore inerziale. D’altra parte è anche (invertendo il segno) l’accelerazione centrifuga avvertita dal Papallino.
Veniamo ora al caso del moto con velocità radiale VR nel sistema non inerziale.
Riprendiamo le formule appena scritte in cui compare l’accelerazione di Coriolis AC:
A(Xp) = (+ sinθ*AC/2 + AXpc)*I
A(Yp) = (- cosθ*AC/2 + AYpc)*J
e
A = √[Apc^2 + AC/4 - Ac*(AYpc*cosθ - AXpc*sinθ)]
Si tratta dell’accelerazione totale vista dall’osservatore inerziale: il moto a velocità costante VR del papallino appare accelerato (ed introduce i termini (+sinθ*AC/2 e -cosθ*AC/2) perché è accelerato il sistema in cui si manifesta.
D’altra parte è anche l’accelerazione fittizia (centrifuga+coriolis) avvertita dal papallino.
Se mi autorizzi inserisco la prima parte della trattazione (moto circolare uniforme) così abbiamo il papiro completo.
accordato!!!!!
Dopo aver chiesto (ed ottenuto) l'autorizzazione di Enzo, pubblico la mia soluzione che sembrerebbe essere corretta.
Questa parte è riferita al solo moto circolare uniforme, come richiesto nel quiz.
Tutto ciò che ho precedentemente pubblicato va posto di seguito a questa sezione, essendone la logica conseguenza nel caso in cui la traiettoria non sia circolare; si tratta comunque di farneticazioni della mia mente malata. Abbiate pazienza.
Bene, partiamo.
Orientiamo il piano cartesiano fissando nell’asse delle ascisse (x) il senso positivo verso destra e nell’asse delle orinate (y) il senso positivo verso l’alto.
Il senso di rotazione positivo sarà quello antiorario che avrà origine (θ=0) in corrispondenza dell’asse delle ascisse.
La generica posizione del papallino nel punto P sarà fornita dalle seguenti coordinate:
Xp = R*cosθ*I (1)
Yp = R*sinθ*J (2)
Dove compaiono le coordinate polari (R;θ) a legare quelle rettangolari (X;Y). I e J sono i versori dei due assi coordinati X e Y.
Posso ora differenziare le due formule precedenti:
d(Xp) = -R*sinθ*dθ*I
d(Yp) = +R*cosθ*dθ*J
essendo R costante (moto circolare).
Divido entrambe le formule per dT (differenziale del tempo):
d(Xp)/dT = -R*sinθ*(dθ/dT)*I
d(Yp)/dT = +R*cosθ*(dθ/dT)*J
Sapendo che (dθ/dT)=ω e che la derivata di uno spazio rispetto al tempo rappresenta una velocità, posso scrivere:
VXp = -R*ω*sinθ*I (3)
VYp = +R*ω*cosθ*J (4)
Essendo costante anche ω (moto circolare uniforme).
Ho ottenuto le due componenti (secondo X e Y) della velocità periferica del papallino nel suo moto circolare. Muovendosi “in tondo” è continuamente sottoposto ad una componente orizzontale ed ad una componente verticale della velocità.
La velocità totale si ottiene sommando i due vettori:
V = -R*ω*sinθ*I+R*ω*cosθ*J = (R*ω)*(-sinθ*I+cosθ*J)
Il vettore (-sinθ*I+cosθ*J) è diretto tangenzialmente alla circonferenza, nel punto P.
Possiamo dimostrarlo considerando il triangolo rettangolo di cui
-sinθ*I e +cosθ*J sono i cateti. L’angolo al vertice di tale triangolo vale θ, essendo (R*ω*sinθ)/R*ω*cosθ) = tgθ. Una semplice costruzione geometrica mostra allora la condizione di tangenza del vettore V alla circonferenza.
Il modulo del vettore V vale:
V = R*ω*√(sinθ^2 + cosθ^2) = R*ω
V = R*ω
Passo ora a differenziare le due formule precedenti:
d(VXp) = -R*ω*cosθ*dθ*I
d(VYp) = -R*ω*sinθ*dθ*J
Divido entrambe le formule per dT (differenziale del tempo):
d(VXp)/dT = -R*ω*cosθ*(dθ/dT)*I
d(VYp)/dT = -R*ω*sinθ*(dθ/dT)*J
Sapendo che (dθ/dT)=ω e che la derivata di una velocità rispetto al tempo rappresenta un’accelerazione, posso scrivere:
AXp = -R*ω^2*cosθ*I (5)
AYp = -R*ω^2*sinθ*J (6)
Ho ottenuto le due componenti (secondo X e Y) dell’accelerazione del papallino nel suo moto circolare. Muovendosi “in tondo” è continuamente sottoposto ad una componente orizzontale ed ad una componente verticale dell’accelerazione.
L’accelerazione totale si ottiene sommando i due vettori:
A = -R*ω^2*cosθ*I-R*ω^2*sinθ*J = (R*ω^2)*(-cosθ*I-sinθ*J)
Il vettore (-cosθ*I-sinθ*J) è diretto radialmente alla circonferenza, nel punto P, puntando verso il centro della circonferenza.
Possiamo dimostrarlo facendo considerazioni analoghe a quelle già fatte in relazione alle velocità. Abbiamo quindi trovato che l’accelerazione è effettivamente centripeta.
Il modulo del vettore A vale:
A = R*ω^2*√(sinθ^2 + cosθ^2) = R*ω^2
A = R*ω^2
Ah ah ah, scusate ma questa è fantastica.
Mi sono accorto solo ora che nella parte iniziale del precedente messaggio ho definito l'asse delle Y asse delle orinate.
Vi prego cortesemente di astenervi, anche se sofferenti di prostata!

caro Alvy... se mi permetti domani o dopo pubblico la soluzione "ufficiale" che è leggermente più rapida anche se del tutto analoga... Ufficiale sta per "MIA": viva la democrazia!!!!!!!!
Beh, non so se permettertelo, sai non vorrei che prendessi l'abitudine...
Vabbè, per stavolta farò un'eccezione, ma solo stavolta!