QUIZ: in giostra su Papalla**
Il gioco che presentiamo è estremamente semplice e ha un ruolo molto importante in fisica. Non è difficile vederci un legame con il moto di precessione dell’asse terrestre… (ops… papalliano…)
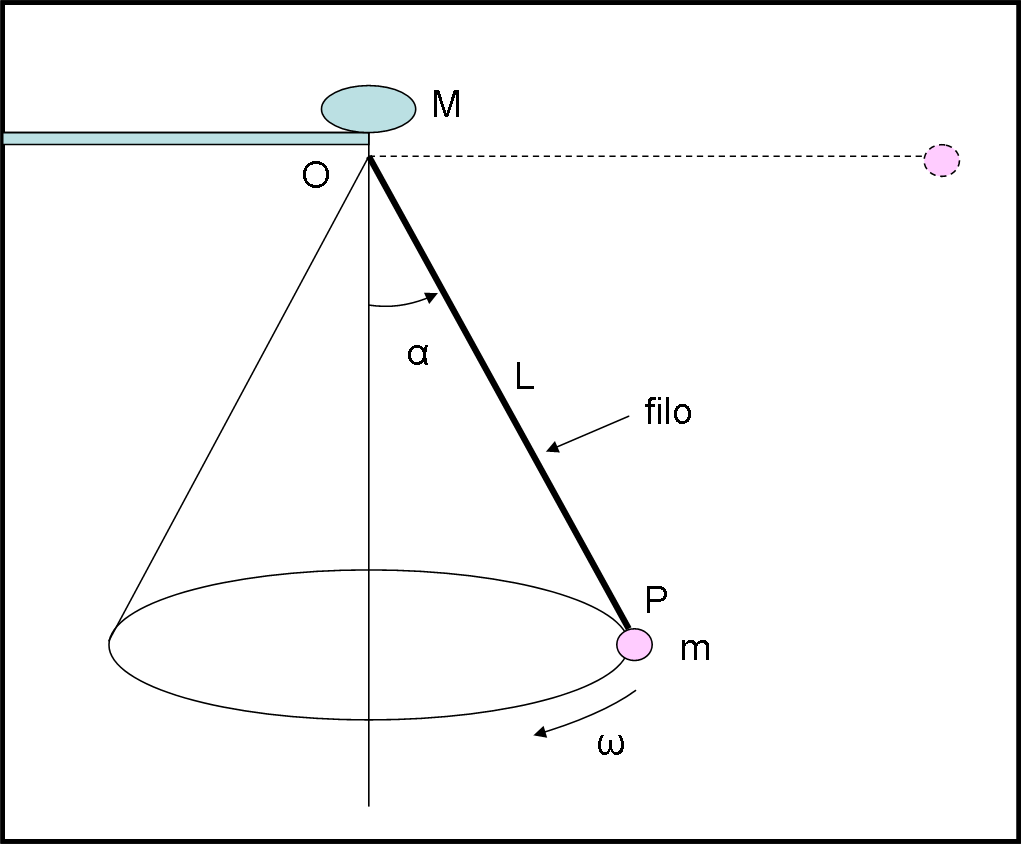
I papalli usano un filo di una lega di germanio, zirconio e iridio sottilissimo, inestensibile e indistruttibile. Un capo è sistemato su un asta collegata con un motorino M che lo mette in rotazione, all’altro capo si sistema il papallo P. In condizione di riposo il papallo è appeso al filo in verticale perfetta. Azionando il motore si imprime un movimento circolare al filo e al papallo, che si sviluppa su un piano orizzontale.
Chiamiamo L la lunghezza del filo, ω la velocità angolare di rotazione e m la massa di papallo P (il filo non pesa). α sia l’angolo tra direzione verticale e filo in rotazione. Come già sappiamo, la gravità su Papalla è uguale a quella della Terra.
La domanda vera e propria è la seguente: “Che velocità angolare deve essere impostata affinché il papallo riesca ad assumere la posizione orizzontale tratteggiata?”
In realtà, è molto più interessante trovare il legame che lega la velocità di rotazione con l’angolo α o qualche altro parametro geometrico corrispondente. Ovviamente, sarebbe auspicabile disegnare un grafico che mostri l’andamento della funzione corrispondente. Insomma, volendo c’è da divertirsi un sacco con questi pochi mezzi a disposizione.
Non vi è certo sfuggita la somiglianza quasi perfetta con una delle giostre più comuni dei Luna Park terrestri, quella con i seggiolini in rapida rotazione.






10 commenti
..... a Roma altrimenti detti, con leggiadro appellativo, calcinculo!
scusate l'off topic
http://www.repubblica.it/scienze/2015/03/14/foto/un_oceano_dentro_ganimede_contiene_piu_acqua_di_tutta_la_terra-109499356/1/?ref=HRESS-3#1
solo sensazionalismo o notizia è seria?
caro Peppe,
sembrerebbe di sì... Volevo inserire la notizia insieme alle sorgenti idrotermali di Encelado. Spero di farlo entro oggi (se non sorgono nuovi impegni...)
Beh, mi sembra sia sufficiente imporre la condizione di equilibrio, solo che .......
Senza voler dare la mia soluzione, ho voluto fare un piccolo calcolo introducendo determinate ipotesi.
Le ipotesi sono le seguenti:
- l'angolo α valga 89° e non 90°
- il filo sia lungo circa 14,5 metri
In questo caso, se non ho sbagliato i calcoli, la velocità angolare dovrebbe essere quella di un oggetto capace di completare la traiettoria circolare in un secondo.
E' corretto Enzo?
ma io voglio proprio 90° !!!! e una bella funzioncina....
e una bella funzioncina.... 
e magari qualche formuletta....
E vabbè, allora devo dare la soluzione!!!!
In quanto al grafico della funzione, devo rinunciarci, visto che non ho la più pallida idea di come si possa disegnare su quest'accidenti di aggeggio tecnologico che chiamate computer!


Se vuoi ti mando in privato un bel disegnino fatto a mano: è il massimo che la mia abilità tecnologica mi consente!
E poi scusa, a che ti servono i 90°? Tanto non ci arriverai mai .....
e dimostramelo!!!!!
Allora vuoi la guerra!!!

Va bene, ecco la mia soluzione.
Una prima considerazione qualitativa ed intuitiva mi porta a concludere che nessun valore, per quanto alto, di ω, potrà consentire all’angolo al vertice α di raggiungere il valore di 90°.
Perché?
Beh, la forza centrifuga che agisce orizzontalmente è limitata dalla forza peso. Facendo la composizione vettoriale tra le due otterrò, in ogni caso, un vettore somma con una componente verticale non nulla.
Passiamo alla dimostrazione analitica.
Consideriamo una generica condizione di equilibrio, ovvero la condizione in cui il peso percorre un’orbita circolare (ovviamente in un piano orizzontale), quale che sia il valore di α.
Sul peso agiscono le seguenti forze:
- La forza centrifuga, agente orizzontalmente verso l’esterno, pari a Fc = m*R*ω^2
- La forza peso, agente verso il basso, pari a Fp = m*g
- La reazione del filo, agente lungo il filo stesso verso l’interno, pari a Fl.
R è la distanza del peso dall’asse di rotazione.
Perché il peso si muova orizzontalmente (α costante) è necessario che sia nulla la forza totale diretta normalmente al filo stesso (nel piano individuato dal filo, dalla forza centrifuga e dalla forza peso).
Calcoliamo le componenti in questione.
- Il contributo della forza centrifuga vale: m*R*ω^2*cosα
- Il contributo della forza peso vale: m*g*sinα
Uguagliamo ora i due contributi:
R*ω^2*cosα = g*sinα
Essendo:
R = L*sinα
possiamo scrivere:
L*sinα*ω^2*cosα = g*sinα
da cui:
ω^2 = g/(L*cosα)
ovvero:
ω = √ [g/(L*cosα)]
Se pongo α=90°, cioè cosα=0,
ottengo che ω → ∞
Disegnando il grafico, o anche sviluppando semplici calcoli, si vede come per:
α = 80° ; ω = 2,40*√( g/L)
α = 89° ; ω = 7,57*√( g/L)
α = 89,999° ; ω = 239*√( g/L)
Mi ricorda un po’ le formule della relatività, nelle quali gli effetti relativistici compaiono in modo “esplosivo” quando già si è prossimi a C.
Per il disegnino del grafico mi rimetto alla clemenza ... della corte e chiamo in aiuto il buon Paolo che ne sa una più del diavolo!