Nel sistema vi sono tre forze in gioco che agiscono su papallo P: la forza di gravità, la forza centripeta e la tensione T del filo.

Affinché papallo ruoti di moto circolare uniforme su un piano orizzontale, attorno all’asse verticale, è necessario (1) che la forza centripeta sia uguale alla componente della tensione parallela ad essa (orizzontale); (2) che la forza peso sia uguale alla componente della tensione parallela alla verticale. Ciò si traduce in:

T sin α = m ω² r      …. (1)

T cos α = mg      …. (2)

Dividendo (1) per (2), ottengo:

tan α = ω² r/g = r/(L cos α)

Da cui:

ω = (g/(L cos α))^1/2

Si ricava subito che se α diventa 90° (giostra che gira in modo perfettamente orizzontale), la velocità angolare diventa infinita. Nessun papallo riuscirà mai a girare lungo la linea tratteggiata!

Studiamo come varia la velocità angolare al variare dell’angolo α

Poniamo y = ω e x = cos α e abbiamo una funzione della forma:

y = (g/L(x))^1/2 = (g/L)^1/2 1/(x)^1/2 = C/(x)^1/2

Abbiamo posto la costante (g/L)^1/2 = C

L’ascissa x può variare solo tra 0 e 1 (i valori negativi tra 0 e -1 sono da escludere dato che la radice quadrata di un numero negativo dà valori impossibili per noi).  Ne consegue che la y può solo andare dal valore C (quando  x = 1, ossia α = 0) al valore + ∞ (quando x = 0, ossia α = 90°).

Studiamo la derivata prima

y = C x^-1/2

y’ = -1/2 C x ^-3/2 = -1/2 C/x^3/2

Nessun valore di x compreso tra 0 e 1 può annullare la derivata

Proviamo con la derivata seconda

y” = -3/4 C x^-5/2 = -3/4 C/x^5/2

Non si annulla nemmeno la derivata seconda e concludiamo che la curva non ha né massimi, né minimi né flessi obliqui.

Conclusione che si poteva capire fin da subito, ma è sempre meglio sfruttare le conoscenze acquisite…

La rappresentazione della funzione è data in Fig. 1

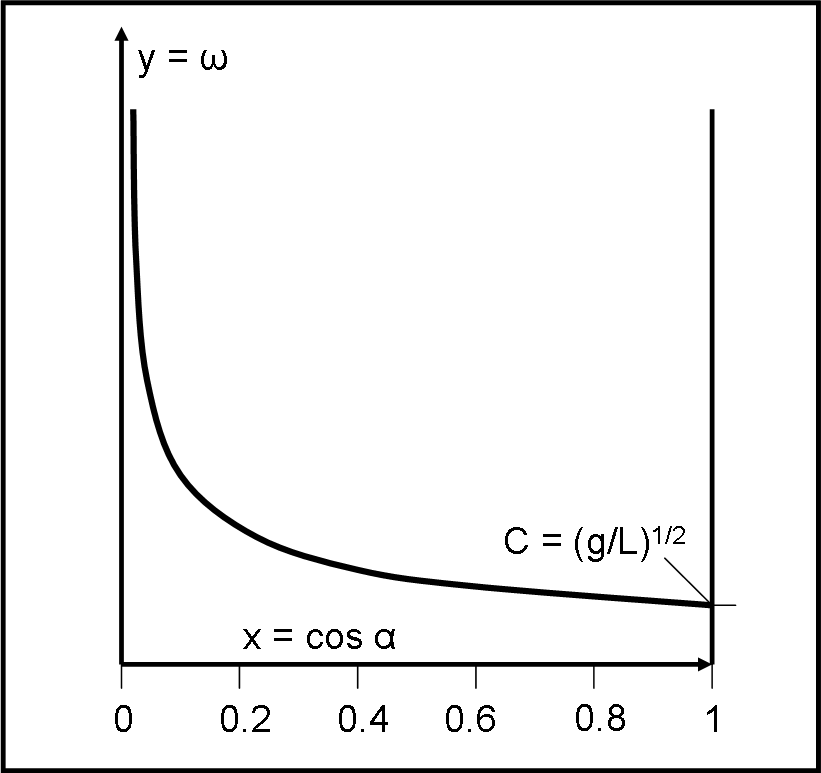
Appendice

Qualcuno potrebbe giustamente dire “Come mai la velocità angolare ha un valore minimo diverso da zero?”. La risposta è abbastanza interessante. In realtà, se non metto in moto il motore M, papallo P può benissimo restare “appeso” al filo in posizione perfettamente verticale. In quella posizione x vale esattamente 1. Sembra , perciò, che il valore di x = cos α = 1 debba portare a un valore di  y = ω = 0.

In realtà, questo ragionamento è vero e nessuno lo confuta. Tuttavia, la giostra ha un senso se papallo P inizia a ruotare con un angolo α diverso da zero e questo fatto implica che si debba raggiungere un valore minimo di ω che dipende sia dalla gravità che dalla lunghezza del filo (in altre parole dalla sua tensione T). Se, infatti, il motore M girasse troppo piano la giostra non si muoverebbe e il papallo resterebbe sempre sulla verticale. E’ quindi necessario che si raggiunga un valore critico della velocità ω. E questo valore critico è quello per cui la x vale 1, ossia proprio per

ω ≥ C = (g/L)^1/2

Non è difficile ricavarlo in altro modo, calcolando, ad esempio, il valore della tensione T

Riprendiamo la (1)

T sin α = m ω² r

Essa si può scrivere:

T sin α = m ω² L sin α

T = m ω² L

Questa è la tensione del filo che cresce con la velocità angolare

Ma vale anche la (2), e quindi:

T cos α = mg

Ossia:

T = m g/cos α

Otteniamo:

m g/cos α = m ω² L

g/cos α = ω² L

cos α = g/ω² L

il valore di ω necessario per avere  il moto di rotazione su un piano orizzontale si ottiene per cos α ≤ 1

Ossia:

g/ω² L ≤ 1

Il che comporta:

ω² ≥ g/L

e, infine:

ω ≥ (g/L)^1/2

Gira, rigira, abbiamo detto la stessa identica cosa di prima…