Categorie: Fisica classica Meccanica Celeste
Tags: conservazione energia energia cinetica energia potenziale evoluzione orbitale orbita parabolica perdita massa solare quiz
Scritto da: Vincenzo Zappalà
Commenti:20
SOLUZIONE del quiz sul “dimezzamento” del Sole. 2 ***
Studiamo con maggiore attenzione ciò che capiterebbe all'orbita terrestre se la massa del Sole dovesse istantaneamente ridursi (trascurando tutti gli effetti di tipo fisico). Il "gioco" è abbastanza interessante. Tuttavia, non pretendiamo di andare ancora oltre... un bel gioco dura poco!
Torniamo, quindi, al nostro Sole che ha deciso di perdere massa improvvisamente (di cui abbiamo parlato in questo QUIZ e nella prima parte della soluzione) e studiamo meglio cosa succede all’orbita della Terra supposta circolare. Introduciamo attentamente le grandezze in gioco.
Un oggetto che si trova in una certa posizione, rispetto a un altro ben più massiccio, è soggetto alla sua forza di gravità e possiede una certa energia potenziale che è massima (ossia uguale a ZERO) quando il corpo è all’infinito, mentre decresce avvicinandosi al corpo centrale. L’energia potenziale è proprio un’energia “in potenza”. Ossia è capace di trasformarsi in movimento e diventare energia cinetica. In realtà l’energia potenziale è sempre negativa, dato che corrisponde a un lavoro che viene compiuto opponendosi alla forza e quindi il valore assoluto dell’energia potenziale cresce avvicinandosi al corpo centrale, ma l’energia è sempre più piccola. D’altra parte, più si è vicini e meno lavoro si deve compiere per opporsi alla gravità e raggiungere quel punto.
Come già detto, l’energia potenziale è sempre legata strettamente all’energia cinetica che dipende dalla velocità del corpo che subisce la forza di gravità. Se portiamo un oggetto a un’altezza h e poi lo lasciamo libero, esso ha acquistato una certa energia potenziale, che viene trasformata in energia cinetica mentre il corpo cade sempre più velocemente verso il corpo centrale.
La condizione fondamentale è che se il sistema (corpo centrale più oggetto orbitante) non cambia, l’energia totale dell’oggetto che subisce la forza di gravità deve rimanere costante. In altre parole, la somma di energia cinetica ed energia potenziale deve rimanere costante.
L’esempio più classico è sempre quello dell’ottovolante. Il carrello viene portato in alto in modo da aumentare la sua energia potenziale (diminuisce il suo valore assoluto). Poi viene lasciato libero ed acquista una velocità di caduta (ossia energia cinetica) a scapito dell’energia potenziale che diminuisce (aumenta il valore assoluto).
L’energia potenziale è come un “portafoglio” pieno di soldi. Finché stanno lì dentro sono una ricchezza “potenziale”. Appena si cominciano a spendere diventano qualcosa di pratico (energia cinetica) che rendono concreta la ricchezza. Purtroppo, però, il portafoglio è costretto a svuotarsi… Arrivati in fondo all’ottovolante abbiamo il portafoglio vuoto, ma tanti oggetti acquistati. Niente vieta, però, di rivendere gli oggetti acquistati e tornare in possesso dei soldi (ossia il carrello torna verso l’alto). Dobbiamo solo tenere presente che, nel mondo della meccanica classica (senza “attriti”, invidia, gelosia, egoismo, e cose del genere), vige una legge di un’onestà perfetta: ciò che si è comprato, si può rivendere allo stesso prezzo che si è pagato. Rivendendo tutto si ha di nuovo il portafoglio pieno (si è tornati col carrello all’altezza iniziale). Si sono persi gli oggetti comprati (si perde l’energia cinetica), ma si riempie di nuovo il portafoglio (energia potenziale).
La situazione cambia se un oggetto si pone in orbita circolare attorno al corpo centrale di massa M. In questo caso l’energia cinetica è dovuta alla velocità di rivoluzione del corpo in orbita. Le due energie devono, comunque, sempre essere legate tra loro. In tale caso, però, vi sono ben poche possibilità di azione. La situazione è molto più rigorosa. L’energia potenziale rimane COSTANTE dato che l’oggetto ruota attorno al corpo centrale sempre alla stessa distanza (il raggio R). Se non cambia l’energia potenziale, non può nemmeno cambiare l’energia cinetica (la loro somma deve restare costante) e l’oggetto si muove con una certa velocità di modulo costante che dipende dal raggio orbitale. Siamo in condizioni di equilibrio dinamico.
Scriviamo quanto detto con il linguaggio matematico:
Energia cinetica = EC = ½ m v2
Dove m è la massa dell’oggetto orbitante e v la velocità orbitale. Notiamo che questa energia SEMBRA scollegata totalmente dalla massa centrale M. Il fatto che non compaia M vuol dire che, in qualche modo, essa può “sopravvivere” inalterata anche se dovesse cambiare M. Teniamolo bene a mente…
Energia potenziale = EP = - GMm/R
Sappiamo già bene perché compare Il segno “meno”. R è la distanza a cui si trova l’oggetto orbitante, ossia il raggio orbitale.
L’energia totale orbitale, che deve conservarsi, è data dalla somma di queste due energie:
Etot = EC + EP = ½ m v2 - GMm/R
Queste semplici considerazioni potrebbero già darci una risposta molto provvisoria e “brutale”. Se cambio la massa M del Sole, cambia l’energia potenziale e potremmo dire che la velocità deve cambiare per mantenere l’energia totale. Arriveremmo a un assurdo, però. Alla stessa distanza R (nessuno ci impone di cambiarla) manterremmo un oggetto in orbita con una velocità maggiore. Le cose non possono andare così. L’errore commesso è stato quello di voler conservare l’energia totale! Essa deve conservarsi SOLO se non cambia il sistema, ma in questo caso il sistema è cambiato, dato che è cambiata la massa del Sole. In poche parole, cambiare la massa del Sole vuol dire cambiare l’energia del sistema. Anche questo è un punto da tener bene a mente.
Ritorniamo alla nostra energia totale con il Sole “normale” e riscriviamola:
Etot = ½ m v2 - GMm/R
Intanto, possiamo tranquillamente “eliminare” la massa m, dividendo tutto per m. Otteniamo un’energia per unità di massa che ci semplifica i calcoli senza cambiare sostanzialmente niente.
Etot = ½ v2 – GM/R
Siamo su un’orbita circolare e la Terra ha una sua velocità che può essere tranquillamente calcolata attraverso la terza legge di Keplero. Oltretutto essa è una velocità costante dato che l’orbita è circolare. Lo abbiamo già fatto la volta scorsa e si trova che.
v2 = GM/R
Come vedete siamo riusciti a scrivere la velocità in funzione della massa M e del raggio dell’orbita.
L’energia cinetica (divisa per la massa m) diventa allora.
EC = GM/2R
Accidenti! E’ esattamente la metà dell’energia potenziale divisa per la massa m. Essa infatti vale proprio, in modulo, GM/R
Non meravigliatevi… abbiamo trovato che l’energia potenziale "regala" l’equilibrio al sistema, se l’energia cinetica è esattamente la sua metà. Non abbiamo fatto altro che scrivere il teorema del viriale (ricordate?). In ogni modo, torniamo alla nostra energia totale che può scriversi in modo estremamente semplificato:
Etot = GM/2R – GM/R = - GM/2R
L’energia totale orbitale non è altro che la metà dell’energia potenziale e dipende essenzialmente dal raggio R dell’orbita (M è sempre quella che è). In altre parole, l’energia orbitale è una costante per un certo raggio orbitale.
Cosa succederebbe se l’orbita fosse ellittica? Niente di veramente speciale… L’unico fatto importante sarebbe la variazione continua e periodica della distanza R. Ciò comporta un continuo cambiamento dell’energia potenziale e quindi di quella cinetica e, infine, della velocità. Per conservare l’energia orbitale, insomma, l’oggetto deve andare più veloce al perielio e più lento all’afelio. Tutto qui. Chi comanda è, comunque, sempre la conservazione dell’energia orbitale.
In conclusione, si trova che l’energia orbitale è una funzione del solo semiasse dell’orbita. Ne segue che l’energia orbitale di un’orbita circolare di raggio R è la stessa di un’orbita ellittica di semiasse a = R. In altre parole, l’energia non dipende assolutamente dall’eccentricità orbitale. L’unica differenza è che mentre nell’orbita circolare le due energie si mantengono sempre uguali, in quella ellittica continuano a cambiare, mantenendo, però, sempre uguale la loro somma.
A questo punto abbiamo in mano tutte le informazioni per studiare ciò che capita se il Sole perdesse parte della sua massa. Torniamo a un’orbita circolare e alla nostra Terra. Abbiamo già visto come è semplice il caso in cui il Sole sparisse del tutto: la Terra proseguirebbe di moto rettilineo uniforme con una velocità che è uguale in modulo alla velocità orbitale che aveva quanto girava attorno al Sole. Una prova in più che la velocità orbitale è in qualche modo indipendente dalla presenza del Sole. Esso non fa altro che obbligarla a cambiare continuamente direzione, ma non può cambiargli il modulo.
D’altra parte, basta prendere la formula dell’energia e azzerare M. Otteniamo:
Etot = ½ v2 – GM/R = ½ v2 – 0 = ½ v2
L’energia è solo cinetica e rimane esattamente quella del moto circolare. La direzione è costante e la Terra se ne va “per la tangente” con velocità v. Ovviamente, l’energia totale non si è conservata dato che è cambiato il sistema, avendo annullato il Sole, la sua forza di gravità e l’energia potenziale.
Passiamo a casi meno drastici e più generali.
Scriviamo nuovamente l’energia dell’orbita originaria, tenendo conto del legame tra energia cinetica ed energia potenziale. Si ha:
Etot,O = GMO/2aO – GMO/aO = - GMO/2aO
Abbiamo solo inserito il semiasse aO di una ipotetica orbita ellittica, che nel nostro caso vale proprio R, sapendo che l’energia non cambierebbe.
Iniziamo a diminuire la massa solare…
Ciò che capita immediatamente è che cambia l’energia potenziale. L’energia cinetica, invece, resta quella che è. Possiamo scrivere:
Etot,N = EC,O – EP,N = GMO/2aO – GMN/aO …. (1)
Notate che abbiamo indicato con indice “N” le quantità moficate (Nuove) e con indice O quelle originali.
Tuttavia, in questa nuova situazione, abbiamo che l’energia potenziale è diminuita in valore assoluto ed è, quindi, aumentata come valore negativo. L’energia cinetica è rimasta uguale e quindi l’energia totale è aumentata solo in base all’energia potenziale. Ne segue che l’orbita deve allargarsi. Ma se l’orbita si allarga, la velocità deve scendere. Oltretutto allargandosi l’orbita, aumenta ancora l’energia potenziale. La configurazione finale, stabile, deve portare (come ormai sappiamo molto bene) a un valore dell’energia cinetica pari alla metà dell’energia potenziale, ossia:
Etot,N = - GMN/2aN …. (2)
L’energia (1) diventa (2), ma deve rimanere sempre uguale, dato che in entrambi i casi stiamo usando la nuova massa solare, ossia uno stesso sistema. Siamo di fronte a un processo di assestamento orbitale.
Uguagliando le due relazioni si ottiene:
GMO/2aO – GMN/aO = - GMN/2aN
Moltiplicando entrambi i membri per 2aN/GMO, otteniamo:
2GMOaN/(2aO GMO) – 2GMNaN/(aOGMO) = - (GMN/2aN) (2aN/GMO)
aN/aO – 2aNMN/MOaO = - MN/MO
e ancora:
aN/aO (1 – 2MN/MO) = - MN/MO
aN/aO = - (MN/MO)/(1 – 2MN/MO)
aN/aO = (MN/MO)/(2MN/MO – 1) …. (3)
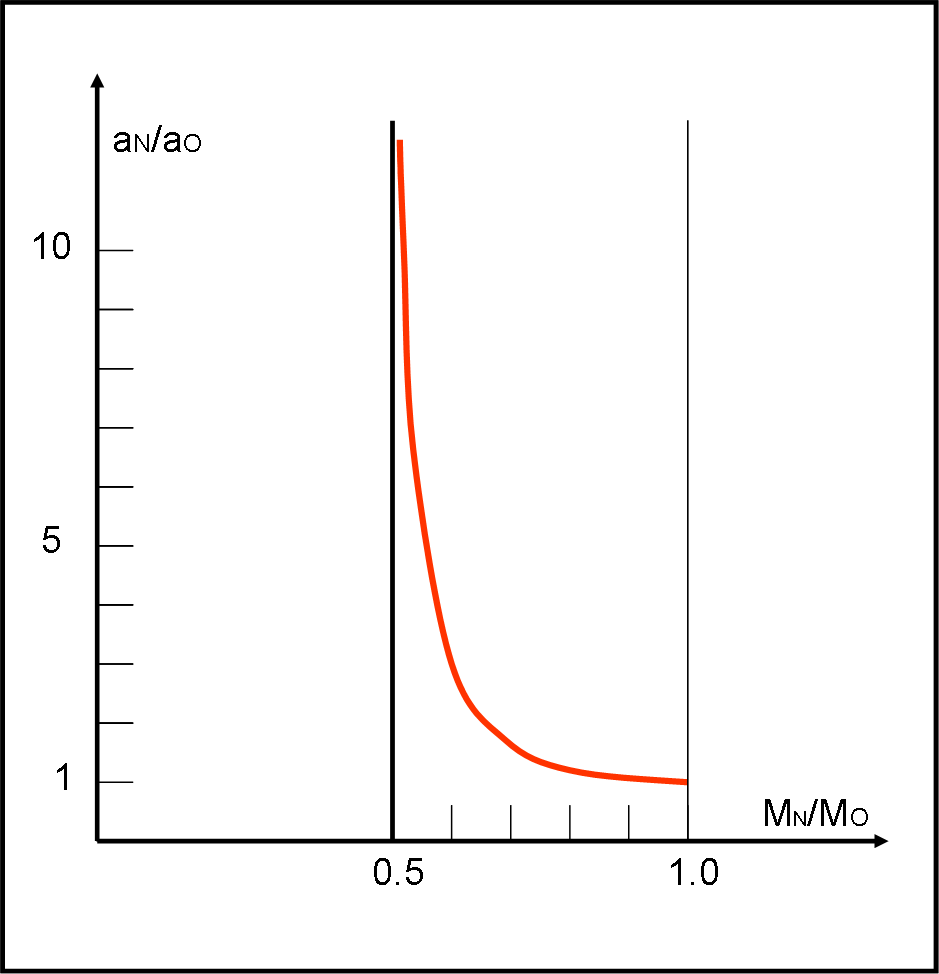
Questa formula permette di calcolare il nuovo semiasse in funzione della variazione di massa solare.
Studiamo rapidamente questa funzione, ponendo y = aN/aO e x = MN/M0.
y = x/(2x – 1)
Se il Sole diminuisce la propria massa, il valore di x è compreso (teoricamente) tra 1 e 0. Tuttavia, stiamo molto attenti al valore x = ½. Per quel valore il denominatore della funzione va a zero e la y va a infinito. Possiamo quindi solo permetterci una perdita di massa minore di 0.5 se no… addio caro Sole! Notiamo anche (potete provarlo facilmente) che per x vicino a 1 la variazione del’asse è molto contenuta, ma se si avvicina a 0.5 il semiasse aumenta in modo rapidissimo. Non esistono massimi o minimi dato che la derivata prima non si annulla mai (provate…).
Ne consegue che poco interessa scendere a valori di x minori di 0.5 dato che per quel valore il semiasse va a infinito e quindi la Terra abbandona il Sole su una traiettoria parabolica, come già avevamo trovato la volta scorsa. In realtà, avremmo orbite iperboliche fino a raggiungere una situazione degenere (retta) per x = 0. Tuttavia, è inutile esagerare con calcoli puramente accademici…
La funzione è rappresentata nella figura che segue.






20 commenti
Benone Enzo, lo sviluppo analitico mi sembra del tutto soddisfacente.
Rimane aperta la questione dell'eccentricità dell'orbita "finale".
Come hai giustamente scritto a proposito della formula risolutiva: "Questa formula permette di calcolare il nuovo semiasse in funzione della variazione di massa solare".
Ma, ed anche questo è stato evidenziato, allo stesso semiasse corrispondono infinite ellissi tutte "portatrici" della stessa energia totale.
Diciamo allora che, su base esclusivamente energetica, non si può fare una scelta. D'altra parte la sparizione istantanea di una massa rilevante costituisce solo un esperimento mentale, assurdo nella pratica.
La fase di assestamento reale, in concomitanza con diminuzioni di massa reali, deve allora prendere molto tempo ed il processo analitico assumerà uno sviluppo iterativo che conduce a ragionare sugli elementi di massa dM che vengono via via sottratti alla creazione del campo gravitazionale.
Se l'espulsione avvenisse con maggiore intensità in una direzione si avrebbe uno squilibrio gravitazionale, rispetto al campo perfettamente radiale, tale da modificare forse l'eccentricità dell'orbita di arrivo, trasformando la circonferenza in ellisse.
Mi sembra di poter dire che in fondo le orbite circolari non esistono, nel senso che l'apastro sarà sempre differente dal periastro, per quanto i due valori possano essere vicini.
Nel caso della Terra, la cui orbita è considerata circolare, la differenza è di circa 5 milioni di chilometri, vale a dire oltre dieci volte la distanza Terra-Luna.
Comunque Enzo, grazie dell'approfondimento.
Scusami Enzo, in soldoni sarebbe che, per tenere il pianeta in orbita (per quanto "larga") si può ridurre la massa del sole al max del 50%, oltre il pianeta se ne scappa via (su una traiettoria iperbolica). Corretto?
Yes Mik, direi che è proprio così.
Volendo fare i precisini si dovrebbe dire che per M'=0,5*M l'orbita diviene parabolica, mentre per M'<0,5*M la traiettoria sarà iperbolica. All'atto pratico cambia poco: il Sole non lo rivedremmo più in entrambi i casi!
Ma quando il Sole diverrà una gigante rossa andrà perdendo massa in modo continuo e graduale ed ancor più ne perderà quando espellerà la nebulosa planetaria. Cosa succederà, escludendo i fenomeni fisici?
Mah, penso che l'orbita potrebbe davvero cambiare la sua eccentricità a seguito di espulsioni asimmetriche di gas con il continuo spostamento del centro di massa del sistema.
Insomma, vattelapesca!
Ovviamente, parabola come caso limite che demarca ellisse e iperbole.
Certo sarebbe interessante analizzare cosa succede se un guscio sferico di massa si stacca dal Sole, ammettendo che la Terra non vaporizzi nel frattempo. Probabilmente non succede nulla fin quando il guscio non supera il raggio di 1UA, dopodiché si ricade nel caso descritto da Enzo e la terra assume la nuova orbita (o se ne va).
cari amici,
ieri sono stato assente tutto il giorno (dalle 10 alle 19 all'ospedale di Cuneo...). Tutto per cercare di risolvere un circolo chiuso sull'infezione al gomito di Barbara. Se non passa l'infezione non possono operarla in testa; l'infezione potrebbe passare ma solo togliendo la placca dal gomito; la placca può essere tolta solo fra qualche mese. Sembra uno dei tanti quiz che vi propongo... Conclusione? Siamo andati a Cuneo e siamo riusciti a farla vedere sia dall'ortopedico che l'ha operata al gomito sia dall'infettivologo (che brutto nome!). Ovviamente il tutto attraverso il pronto soccorso e i suoi... tempi...
Fortunatamente (si fa per dire) le hanno dato una serie di esami da fare che dovrebbero chiarire del tutto se c'è o non c'è l'infezione, a che livello è e se può essere estirpata con i soli antibiotici (certi esami più rapidi non può farli a causa della operazione troppo recente alla testa...). Va beh... un passo in avanti e da oggi cominciamo con le prenotazioni e con i primi esami...sperando nei tempi ospedalieri. Intanto, potrebbe avvicinarsi il momento di togliere la placca (sembra che l'osso sia abbastanza ben risaldato). Insomma... una stanchezza mostruosa!!!
In ogni modo, vedo che Mik e Alvy se la sono cavati benissimo da soli!!!!!
Mi scuserete se riprendo quanto scritto in un precedente commento, relativamente alla determinazione dell'asse maggiore dell'ipotetica ellisse in cui si potrebbe trasformare la circonferenza iniziale a seguito dell'improvvisa diminuzione di masa solare.
Il fatto è che mi sono accorto di aver commesso un errore nel portare in conto la nuova massa solare all'interno dell'espressione matematica dell'energia cinetica corretta: ciò conduceva ad un evidente assurdità che non riuscivo a spiegarmi.
Siccome non mi piace mettere in giro informazioni errate, sorbitevi questa errata-corrige :
:
Immaginiamo che la massa del Sole divenga improvvisamente pari a 0,7 masse iniziali.
M’ = 0,7*M.
L’energia potenziale diviene (istantaneamente):
EP’ = -0,7*G*M*m/R
D’altra parte l’energia cinetica (istantanea) rimane costante, almeno al momento dell'evento:
EC = 0,5*EP = 0,5*G*M*m/R
L’energia totale (istantanea) sarà allora:
ET’ = EC – EP’ = 0,5*G*M*m/R – 0,7*G*M*m/R, cioè:
ET’ = – 0,2*G*M*m/R
L’energia totale è negativa e l’orbita sarà di tipo chiuso (circonferenza o ellisse). Decido di pormi nella condizione più generale optando per l'orbita ellittica.
So che, nel caso delle orbite ellittiche, la velocità a distanza R dal corpo attraente vale:
V = √[2*G*M*(1/R-1/2a)]
dove a è il semiasse maggiore dell’orbita.
L’energia totale dell’orbita ellittica di arrivo sarà allora:
ET'=-0,2*G*M*m/R=0,5*m*[2*G*0,7*M*(1/R-1/2a)]–0,7*G*M*m/R
Svolgendo i calcoli ricavo che:
a = 1,75*R.
Siccome l'energia totale dell'orbita ellittica dipende solo dal semiasse maggiore a, ho trovato che tutte le infinite (di numero!) ellissi con a=1,75*R, ciascuna con la sua eccentricità, sono ugualmente plausibili.
Da rilevare che anche la circonferenza (che è pur sempre un'.... ellisse con i fuochi sovrapposti) con raggio R'=1,75*R presenta gli stessi requisiti.
Quale orbita sceglierà il nostro derelitto pianeta?
Ai posteri l'ardua sentenza!
Articolo molto interessante.
Mi chiedevo se qualcuno si e' mai preso la briga di calcolare la riduzione di massa solare dovuta alla sola reazione termonucleare che avviene nel suo nucleo, secondo la famosa relazione E=mc2.
E se questa ha effetti apprezzabili sulle orbite dei pianeti.
Ciao.
Paolo
caro Paolo,
leggo solo ora la tua domanda (ero in vacanza senza internet...)...
Sì, sono stati fatti i calcoli, sia per la perdita energetica legata alla radiazione sia per il vento solare. Questi, penso, siano abbastanza accurati...
Il Sole ha una massa di circa 2 x 1030 Kg. La perdita di massa in vento solare si aggira sui 1,2 x 109 kg al secondo, mentre quella per la radiazione è di circa 4,2 x 109 kg. Il totale porta a circa 5,4 x 109 kg al secondo. Ciò implica che il Sole perde circa l'8 x 10-14 % della sua massa ogni anno. Per perdere tutta la sua massa dovrebbero passare ben 1,6 x 1015 anni, ma ben prima il Sole uscirà dalla sequenza principale e la sua evoluzione sarà più rapida e la massa verrà persa più velocemente... Questo calcolo, però, è fuori da ogni stima plausibile...
Grazie tante Vincenzo !
Se e' cosi, la diminuzione di massa rispetto alla massa complessiva appare un'inezia... e gli effetti sulle orbite dovrebbero essere irrilevanti, ma perché dici che e' fuori da ogni stima plausibile ?
Inoltre riflettevo su quanto sopra, e mi son posto qualche interrogativo (e perdona in anticipo la banalita' ... sono davvero un profano con poca domestichezza).
Stante che la velocita' di percorrenza dell'orbita in un certo momento (cioe' l'energia cinetica) e' indipendente dalla massa del Sole (e dalla sua eventuale variazione), se il sole riducesse la sua massa l'orbita si allargherebbe. Ma questo mi porta a pensare che quindi i pianeti piu' esterni hanno velocita' superiori di percorrenza delle loro orbite (altrimenti non sarebbero "esterni"), anche se angolarmente le velocita' sono inferiori, giusto ? In altre parole, lo stesso allargamento dell'orbita lo si otterrebbe anche se al posto di ridurre la massa del sole, la terra aumentasse la sua velocita', dico bene ? Ma se pianeti piu' lontani hanno energia cinetica superiore, questo non confligge con l'assunto iniziale per il quale energia potenziale + energia cinetica sono sempre costanti ?
Evidentemente mi sfugge qualcosa... forse la cosa ha a che fare col fatto che l'attrazione gravitazionale aumenti in modo non lineare in funzione della distanza ?
Seconda cosa : se il sole riducesse la sua massa in tempi successivi... cioe' diciamo un 25% oggi... e un altro 25% (della massa iniziale) tra un milione anni (giusto per lasciare alla terra il tempo di assestarsi su una nuova orbita). Secondo i calcoli qui sopra la terra non lascerebbe il Sole, perché 1/4 della massa solare non e' sufficiente, in nessuno dei due casi ... ma la loro somma in una volta si. Se ne deduce che la gradualita' cambia il risultato finale ?
Ciao. Paolo
caro Paolo,
per quanto riguarda la prima parte, penso che sia sufficiente leggere un ulteriore quiz e relativa soluzione:
http://www.infinitoteatrodelcosmo.it/2015/08/25/quiz-trasferimento-orbitale/
http://www.infinitoteatrodelcosmo.it/2015/08/31/risoluzione-del-quiz-sul-trasferimento-orbitale-satelliti-artificiali-e-il-signor-hohmann/
Per la seconda parte, direi che il 25% del 100% più il 25% del 75% non è uguale al 50% del 100%...
Ciao Vincenzo,
grazie molte, leggero' il quiz con attenzione.
Per la seconda parte, certo hai ragione (in effetti avevo specificato 25% della massa iniziale)... ma la sostanza della questione mi pare fondata. Riduzioni della massa del sole singolarmente inferiori al 50% non comporterebbero una fuga della terra, ma la somma delle stesse riduzioni (purche in totale => di 1/2 della massa), in una volta sola, invece si. Se e' giusto il ragionamento, e' interessante...
caro Paolo, non avevo fatto caso a quel "della massa iniziale"... scusa...
per come è impostata la formula, essa è valida per un cambiamento repentino di una certa massa. Una volta che l'orbita è cambiata e si è assestata è come se fossimo di fronte a una nuova stella e a una nuova Terra. La MN e la Mo cambiano di conseguenza e la formula vale di nuovo per la nuova configurazione. Sono cambiate le energie in gioco... Il confronto con la massa originale M0 non ha più senso, dato che questa è diventata una nuova Mo. Comunque, hai ragione, ci si trova di fronte a un piccolo assurdo che deriva dal voler mantenere valide le configurazioni che ormai non esistono più...
Grazie Vincenzo,
ho approfondito l'altro quiz... davvero bello.
Ho imparato che l'energia cinetica del satellite non si mantiene nel trasferimento orbitale: il satellite riceve un impulso iniziale che ne aumenta la velocita'... ma mentre si allontana dalla terra la perde in favore della distanza, cioe' guadagna energia potenziale...
Caro Paolo,
sono proprio contento di esserti stato utile... Sai le regole della fisica sono sempre le stesse, ma guarda che meraviglia che è l'Universo!!! Spero che continuerai a seguirci, andando a leggere gli approfondimenti, dove troverai di tutto e di più... dalla relatività alla meccanica quantistica e molto altro ancora...
a prestissimo!
Ciao Paolo,
credo che troverai molto interessanti anche questi due articoli
http://www.infinitoteatrodelcosmo.it/2014/12/13/un-buco-nero-fatto-in-casa/
http://www.infinitoteatrodelcosmo.it/2014/12/18/come-abbandonare-gentilmente-un-buco-nero/
nei quali si parla molto di energia cinetica e potenziale e, soprattutto, di un altro caso in cui la "gradualità" di un processo possa cambiarne il risultato finale. Buona lettura!
ottimo consiglio, Dany!
Sono convinto che Paolo li troverà interessanti, se ancora non conosce questa problematica...
Grazie
Salve a tutti,
questo articolo è molto interessante e offre una chiara spiegazione del problema.
Ora sappiamo come si comporta il semiasse maggiore di un'orbita a seconda della massa centrale M, ma tuttavia manca la risposta a un interrogativo collaterale ma importante (e già richiesta in altri commenti):
come varia l'eccentricità al variare della massa centrale M?
Grazie
E.
a parità di semiasse l'eccentricità può essere qualsiasi... non c'è nessuna dipendenza dinamica tra massa ed eccentricità. E' solo una questione di fisica della formazione...
Grazie mille!
Un'altra domanda: non mi è molto chiaro il passaggio logico in base al quale sarei autorizzato a considerare l'espressione Ec = GM/2R valida anche per un'orbita ellittica (valorizzata come Ec = GM/2a, a essendo il semiasse maggiore).
Io nelle formule sto considero Ec costante, usando il valore caratteristico di un'orbita circolare (per la quale Ec è costante), mentre in realtà in un'orbita ellittica Ec varia in continuazione...
Perché sono autorizzato ad usare l'espressione costante nei calcoli?
Grazie ancora
E.
la risposta è legata a quanto detto precedentemente. L'energia istantanea è una cosa, mentre l'energia totale è un'altra. L'energia orbitale dipende solo da a e non da e...